用电数据驱动的低压配电网负荷随机建模及不平衡评估

薛世伟，贾清泉，张珂欣，高志强，梁纪峰，李 洋

（1. 电力电子节能与传动控制河北省重点实验室（燕山大学）,河北省 秦皇岛市 066004；2. 国网河北省电力有限公司电力科学研究院,河北省 石家庄市 050021；3. 国网冀北电力有限公司智能配电网中心,河北省 秦皇岛市 066100）

0 引言

在全球致力于低碳可再生能源转型背景下,居民用电设备发生了很大变化,电采暖、空调、电动汽车以及户用光伏等大功率单相设备越来越多地接入配电网。三相不平衡问题不仅与单相设备的接入分布有关,还受设备随机启停时序的影响,因此规模化大功率单相设备造成的三相不平衡问题日益突出且不确定性增大［1-3］。三相不平衡对电网影响是持续性的［4］,不但会增加配电网损耗,还会造成零线过流、相线过压、设备烧毁,甚至严重时可能造成变压器爆炸［5-7］。单相设备接入的平衡性通常比较明确,即三相不平衡问题主要源于单相设备运行行为不一致。因此,研究单相设备的运行行为是分析三相不平衡问题的基础。

传统确定性方法［8-11］因采用恒定功率模型不能反映负荷和光伏出力的不确定性。为了表示负荷和光伏随机运行行为特征,目前已有文献利用数据挖掘技术,对配电网单相设备运行数据进行统计模拟,并建立其随机模型,研究配电网三相不平衡等电能质量问题。文献［12-13］采用蒙特卡洛模拟方法研究光伏随机容量和位置的不确定,建立光伏随机模型。但该方法并未从时间角度考虑光伏出力变化的不确定。文献［4］基于不同时段负荷功率平均值,通过随机改变功率因数,建立负荷随机模型。但该方法易出现各时段内负荷变化小、不同时段间负荷变化大的问题,与实际相比误差大。文献［14］分别利用多元相关随机数和长时间测量的随机负载模型建立光伏和负荷的随机模型。但该模型过度依赖于采样频率及采样时间,在实际工程中实现难度较大。文献［15-16］基于均匀分布随机生成一定范围内的负荷及光伏输出功率,并建立其随机模型。文献［17-18］采用正态分布和Beta 分布分别建立了负荷和光伏随机模型。但是上述文献［15-18］采用随机处理方式使得各时刻之间的数据没有联系,不能真实体现负荷和光伏输出功率的实际变化情况。

由于上述部分研究采用静态模拟,因此该建模技术仅能体现三相不平衡在某时间断面的超标情况,利用抽样方法生成的序列元素独立随机,而实际电力系统中用户各时刻用电行为联系紧密,采用独立元素抽样难以表征配电网单相设备随机时序运行造成三相不平衡的影响程度。为此,本文基于数据驱动技术,从用户用电行为状态、状态随机时序转移以及电能质量指标计算与评估角度展开研究,采用层次聚类方法划分不同典型用户负荷曲线以减少计算复杂度,并采用用电数据驱动的低压配电网负荷随机建模方法,保证了考虑随机性和时序性后用户负荷建模的精度。

1 用户用电设备集群行为状态建模

考虑配电网居民负荷和光伏等单相设备集群对三相不平衡的影响,建立了用户用电行为的概率模型,并对其状态进行划分。

1.1 居民负荷集群行为状态建模

1.1.1 居民用电概率模型

正态分布能够很好地表征居民用户用电不确定性,其概率模型参数受居民用电行为状态影响［19-21］。居民用户不同时刻用电行为状态差异性较大,本文将居民日负荷分为多种用电行为状态,每种用电状态对应一个正态分布,采用多个正态分布表征用电的不确定性,即用高斯混合分布表征单个居民日用电情况。所建立居民用电的概率密度函数fJ(sL|θ)如式（1）所示。

由通过式（1）建立的用户用电概率模型可知,该模型参数受用电行为状态影响,需要对不同状态进行划分。

1.1.2 居民用电行为状态集群划分

首先,根据用户用电负荷曲线相似程度,结合层次聚类算法划分多类典型用户；其次,对各类典型用户用电行为状态进行高斯混合聚类；最后,对典型用户用电行为状态进行划分并求解其参数。

对居民用户用电规律进行数据挖掘,对各类典型用户用电数据进行状态集群划分,采用最大期望（expectation maximization,EM）算法确定不同用电行为状态下正态分布函数的参数。

假定典型用户用电样本有N个观测数据,K种用电行为状态已知,观测数据来自用电行为状态类别未知,且每个观测数据相互独立。利用EM 算法求解各状态参数,需定义隐变量,为此本文引入隐变量zn,k表示第n个观测数据sL,n来自第k种用电行为

由于zn,k未知,故需对其进行估计。根据贝叶斯定理,可求观测数据sL,n属于第k种用电行为的后验概率,将θk看做常数求式（2）的期望,得到zn,k的期望γ(zn,k)为:

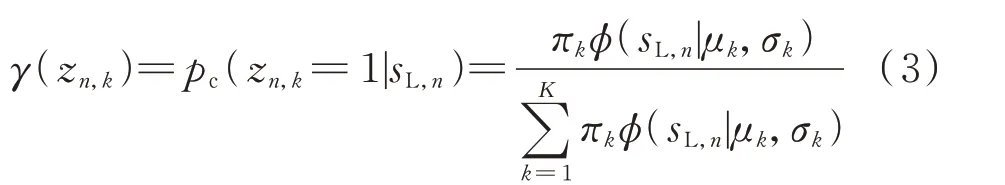
式中:pc(zn,k=1|sL,n)为sL,n已知且zn,k=1 的条件概率。

将γ(zn,k)看做常数对式（2）求导,得到对数似然函数极值点满足的条件,进而得到θk的参数为:

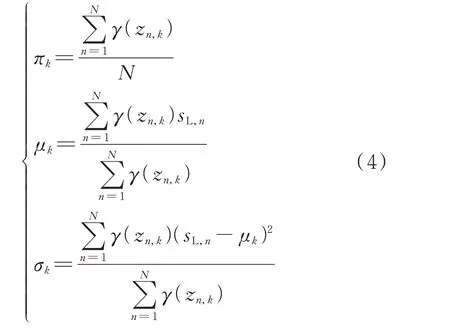
通过迭代E 步和M 步对完全数据极大似然估计进行计算,并实现样本数据分类。具体步骤如下:

步骤1:初始化各类正态分布参数初值θ(0)；

步骤2:令m次迭代后参数估计值为θ(m),通过式（3）计算期望值γ(m)(zn,k)（E 步）；

步骤3:通过式（4）计算参数值θ(m+1),并作为新一轮迭代估计值（M 步）；

步骤4:重复步骤2 和步骤3,直至参数值收敛。

1.2 光伏集群出力状态建模

1.2.1 光照强度概率密度模型

光伏出力与光照强度近似线性相关,而光照强度服从Beta 分布,因此建立光照强度概率密度函数如式（5）所示［17-18,23］:

式中:Beta(·)为Beta 分布函数；αNIr和βNIr为NIr云层状态下Beta 分布参数；PPV,N为光伏并网额定功率；ρIrref为标准光照强度,本文取1 kW/m2。

2 用户用电状态随机时序过程建模

实际生活中居民用电行为和光伏出力变化具有时序性［24-25］。马尔可夫链能够很好地利用设备运行历史数据体现各状态之间的联系,以概率形式反映状态的转移［26］,而序贯蒙特卡洛模拟能够描述系统状态的持续时间。基于该原理,构建系统用电行为状态随机模型。

2.1 居民用电与云层状态转移

1）马尔可夫链原理

假设系统在t时刻处于状态is,下一时刻状态转移到js,通过一步转移的条件概率通常记为pisjs,1(t)=pisjs(t),并称为马尔可夫转移概率。考虑到居民用电行为随机性特点,将居民用电时间和光伏出力时间分别划分为tti和tpvti个时间段进行分析,统计每个时间段内状态转移情况,建立t时刻系统状态转移概率矩阵p(t)为:

式中:ps(t)=[ps,1(t),ps,2(t),…,ps,Ns(t)],其中ps,1(t),ps,2(t),…,ps,Ns(t)分别为t时刻系统处于状态1,2,…,Ns的概率。

定义gs(·)为状态映射函数,即状态is=gs(pis),则由式（10）可以根据状态概率得到下一时刻随机取得的状态。

式中:qc,isjs(t)为光伏在t时刻所在的时间段内由云层状态ics一步转移到状态jcs的样本数。

2.2 状态循环转移

本文通过序贯蒙特卡洛模拟方法对系统状态持续时间进行概率抽样。根据状态转移概率建立状态循环转移过程。通常认为电力系统元件运行状态持续时间是服从指数分布的随机变量［27-28］,建立用户nu在t时刻用电行为状态持续时间抽样值Dnut如式（13）所示。其中该用户在本文中特指居民用户和光伏用户的总称,计算时将两者分别作为一个独立用户处理。

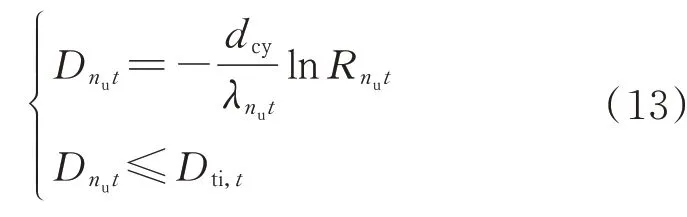
式中:dcy为任意时间段内样本数据采集的时间间隔；Rnut为[0,1]区间均匀分布的随机数,其中Rnut=0 表示系统维持原状态；λnut为用户nu在t时刻用电行为状态转向其他状态的转移概率或固定转移参数；Dti,t为t时刻所在时间段总时长。

本文基于马尔可夫链构建系统用电行为状态转移矩阵,并采用序贯蒙特卡洛模拟方法处理状态持续时间,构建状态转移随机模型。其流程图如附录A 图A1 所示。

3 配电网三相不平衡计算与评估

本文利用辐射状配电网各节点与支路关系,建立节点-支路关联矩阵。同时,基于前推回代思想对配电网潮流进行计算,通过对称分量法计算配电网各节点三相不平衡度［29-31］。

3.1 节点-支路关联矩阵

低压配电网一般以辐射状网络形式运行,通过配电变压器降压后经各支路对各节点居民用户进行供电。辐射状配电网拓扑结构有挂灯笼式结构、树形结构等。本文以挂灯笼式结构为例进行研究。辐射状配电网结构示意图如图1 所示,除去母线节点,该配电网结构可看做由NL条支路和NL个节点组成。其中,取母线侧流向负荷的电流方向为正方向,分布式电源采用和负荷等值反向的方式处理。

图1 中:I˙b,1为配电网首条支路电流,I˙b,nL为支路nL电流,U˙nod,nL为节点nL电压,I˙nod,nL为节点nL注入电流。

图1 辐射状配电网结构示意图Fig.1 Schematic diagram of structure of radial distribution network

对于辐射状低压配电网,本文定义A为3NL×3NL上三角稀疏矩阵的关联矩阵,其中矩阵的行代表节点编号,列代表支路编号。E为3×3 单位矩阵,O为3×3 零矩阵。假设节点iL与支路jL关联,若支路电流正方向流向节点iL,则A(iL,jL)=-E,其中iL=1,2,…,NL,jL=1,2,…,NL；若支路电流正方向背离节点iL,则A(iL,jL)=E。假设节点iL与支路jL不关联,则A(iL,jL)=O。

3.2 三相不平衡度计算

针对配电网三相用户的三相不平衡负荷特殊情况,根据智能电表获取该用户节点相别的电气信息进行计算。另外,本文忽略中性线、地线及线路不对称性对三相潮流计算的影响。

各节点注入电流组成配电网节点电流列向量I˙nod,其中节点nL注入电流计算公式如式（14）所示:

支路电压降可用支路阻抗Zb与支路电流I˙b表示,即ZbI˙b,也可用关联矩阵A与节点电压列向量U˙nod表示,即ATU˙nod。由图1 可知,除去母线节点后,首条支路仅有末端节点,而ATU˙nod中首个元素矩阵是-U˙nodt,1。为便于关联支路电流,设一个NL行列向量U˙s,除首元素矩阵为U˙st外,其他元素矩阵均为O,因此构成式（17）所示关系式:

由式（14）计算得到各节点注入电流；由式（16）计算得到各支路电流；由式（18）计算得到各节点电压,并循环迭代计算。以第n′次和n′-1 次迭代结果的电压差作为收敛条件,如式（19）所示:

步骤2:按式（14）计算各节点注入电流；

步骤3:由式（16）计算各支路电流；

步骤4:由式（18）计算各节点电压；

步骤5:重复步骤2 至步骤4,直至满足式（19）收敛条件。

由上述计算步骤获得各节点电压及其注入电流,参考GB/T 15543—2008《电能质量 三相电压不平衡》［32］中三相不平衡度的计算方法,定义三相电压不平衡度如式（20）所示:

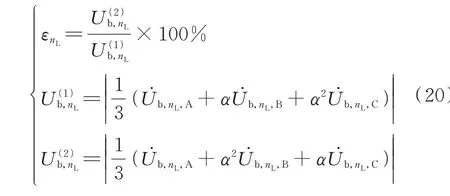
3.3 三相不平衡评估

为提高模拟方法精准度,通常要对配电网各节点用电数据进行多次重复抽样。拉丁超立方抽样（Latin hypercube sampling,LHS）属于分层抽样,主要由采样和排列两步组成,可覆盖随机变量整个分布区间,是一种有效反映随机变量整体分布的方法［33］。本节利用LHS 技术将系统随机模型与三相不平衡估计量计算相结合,通过系统状态随机过程建模、随机变量抽样以及三相不平衡度计算等步骤对低压配电网三相不平衡进行评估。

首先,利用马尔可夫链挖掘系统各状态之间的联系,并采用序贯蒙特卡洛模拟方法对系统状态持续时间进行抽样,建立系统状态随机过程模型；然后,利用LHS 获取各随机变量数据采样矩阵［33］；最后,利用节点-支路关联矩阵对配电网节点电压进行潮流计算,结合数据采样矩阵和统计方法,得到1 d各时刻配电网总馈线处三相不平衡度均值。三相不平衡评估流程如附录A 图A2 所示。

4 仿真分析

本文以邢台地区某农村配电网为例,分析居民用电和光伏出力行为随机性对三相不平衡的影响。本文假设所有单相用户连接相别是已知的［34-35］。该配电网结构如附录A 图A3 所示。

本文将配电网所在地区视为一个确定的经纬度坐标,由HOMER 软件输入指定地点经纬度产生小时级光照数据,根据式（6）获得不同云层划分状态及该状态下光照数据,利用式（5）求出不同云层状态下光照强度概率密度,结合式（7）获得光伏模拟出力情况。需要说明的是,由于本文通过统计某一时间段内系统数据计算系统状态转移概率,基于状态随机持续时长获得系统1 d 内的时序状态,因此光照数据采样和负荷采样时间间隔并不存在时间上的对应关系,两者可以是不同的。在计算光伏出力时假设了所有用户安装光伏时朝向一致,忽略了安装带来的差异。将1 d 内的云层状况划分为lIr1、lIr2、lIr3、lIr4这4 个等级,如表1 所示。表1 中CCL 值越小,表示云层覆盖越少,即等级lIr1表示天气状态最好,等级lIr4表示天气状态最差。

表1 云层覆盖等级分类结果Table 1 Classification results of cloud coverage level

4.1 模型验证

考虑到不易获取农村配电网中的三相不平衡指标实测数据,因此本文利用居民用电实测数据计算指标作为实测计算值进行数据对比,以验证模型的合理性。另外,通常情况下,用户在周末用电相比星期一至星期五用电行为随机性更大,但由于本文获取该典型场景的数据较少,仿真时使用所有数据来表征用户用电行为可能略有偏差,但这不影响本文所提方法的适用性。

农村配电网数据采集时间间隔为15 min,采集总时间为1 个月。以节点相别的功率曲线为基准对其平均日负荷曲线进行层次聚类划分。根据聚类树状图,将其划分为4 种典型曲线进行分析,其中层次聚类树状图见附录A 图A4。图A4 中考虑三相接入位置将每个节点依次扩充为3 个点,总共扩充为72 个点进行聚类划分。

4.1.1 马尔可夫链及状态持续时长分析

以典型用户负荷为例,对马尔可夫链和序贯蒙特卡洛抽样状态持续时长进行分析。根据每种典型日负荷曲线历史信息,生成高斯混合模型及各功率点对应的状态类别。统计并分析各类别信息,生成各时间段的马尔可夫状态转移概率矩阵,并得到各状态之间的联系。以中午12:00 到13:00 时间段为例,对不同种类典型用户的各状态之间转移情况进行分析。四种典型用户在该时段的马尔可夫状态转移概率矩阵和初始状态概率如附录A 式（A1）至式（A5）所示。

根据式（13）可获得系统状态持续时长,结合状态转移概率得到4 种典型用户在1 h 内的状态运行类别如图2 所示。图2 中以各典型用户在每2 个相邻标记点对应的时间差作为该状态持续时长,可以看出,4 种典型用户用电状态类别随时间不断变化。

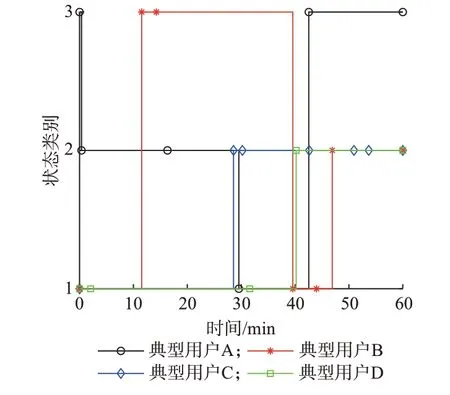
图2 各典型用户用电状态变化曲线Fig.2 Changing curve of power-consumption state for each typical user

对于状态持续时长,以典型用户B 为例,在0 时位于状态类别1,并且该状态持续约11 min 后转移到状态类别3,再持续约3 min 后发生自身状态转移,保持状态类别3 直到40 min 左右时转移到状态类别1,持续4 min 左右后发生自身状态转移,保持状态类别1 直到47 min 左右时转移到状态类别2,直到60 min 时状态结束。

因为高斯模型参数与状态类别对应,所以可根据状态类别变化选择高斯模型,并生成典型用户用电功率曲线。最终根据用电负荷曲线计算配电网潮流。

4.1.2 三相不平衡度分析

为了表征估计精度,本文定义了绝对误差平均值τ,如式（21）所示:

式中:ε′1,ε′2,…,ε′M分别为1,2,…,M时刻不平衡度估计数据；ε1,ε2,…,εM分别为1,2,…,M时刻不平衡度实测计算数据。

根据所生成的用户随机时序负荷曲线,计算配电网不含光伏条件下,末节点24 处三相不平衡度实测计算结果、仿真计算结果,以及文献［4,14-18］方法结果对比如图3 和附录A 表A1 所示,其中实测计算结果为1 个星期内三相不平衡度的平均值,模拟时长为24 h。

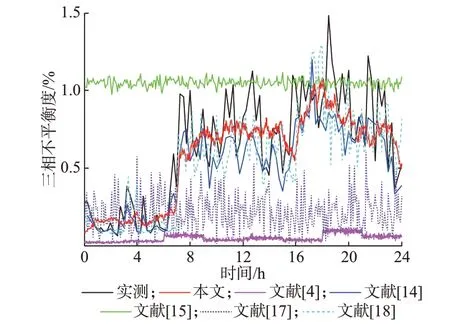
图3 数据对比Fig.3 Data comparison

根据图3 数据对比,计算得到绝对误差平均值τ≈0.15%,仿真模拟数据与实测计算数据具有较高一致性。文献［14］仅能利用以往数据以采样时间间隔为单位模拟各时刻用电状态,且需要更多数据支撑,大量模拟后数据波动范围仍然较大。本文方法相比文献［14］更能从分钟级别精度分析配电网电能质量情况,模型更加精细。从图3 可以看出,文献［4,15,17-18］可以从分钟级等更小时间尺度分析电能质量情况,但是文献［4］基于各时段平均负荷随机改变功率因数生成负荷数据,文献［15］基于均匀分布生成负荷数据,文献［17］基于正态分布生成负荷数据,与实际误差较大；文献［18］在文献［17］基础上加入了各时段正态分布参数进行修正,使其模拟结果与实际结果相比误差较小。从附录A 表A1 平均绝对误差对比中可以看出,相对于上述文献,本文所得平均绝对误差结果更小,体现了本文所建模型的精确性。

从变化趋势上可看出,所提出的模型能体现实际情况,从而验证了所建模型的合理性。

4.2 居民用电影响分析

基于4.1 节,根据配电网居民用电随机性特点分析三相不平衡超标情况。统计1 d 内各时间点的三相不平衡度,分析其超标概率情况如图4（a）所示,每日和每30 min 内超标持续时长累积概率分布分别如图4（b）和图4（c）所示。

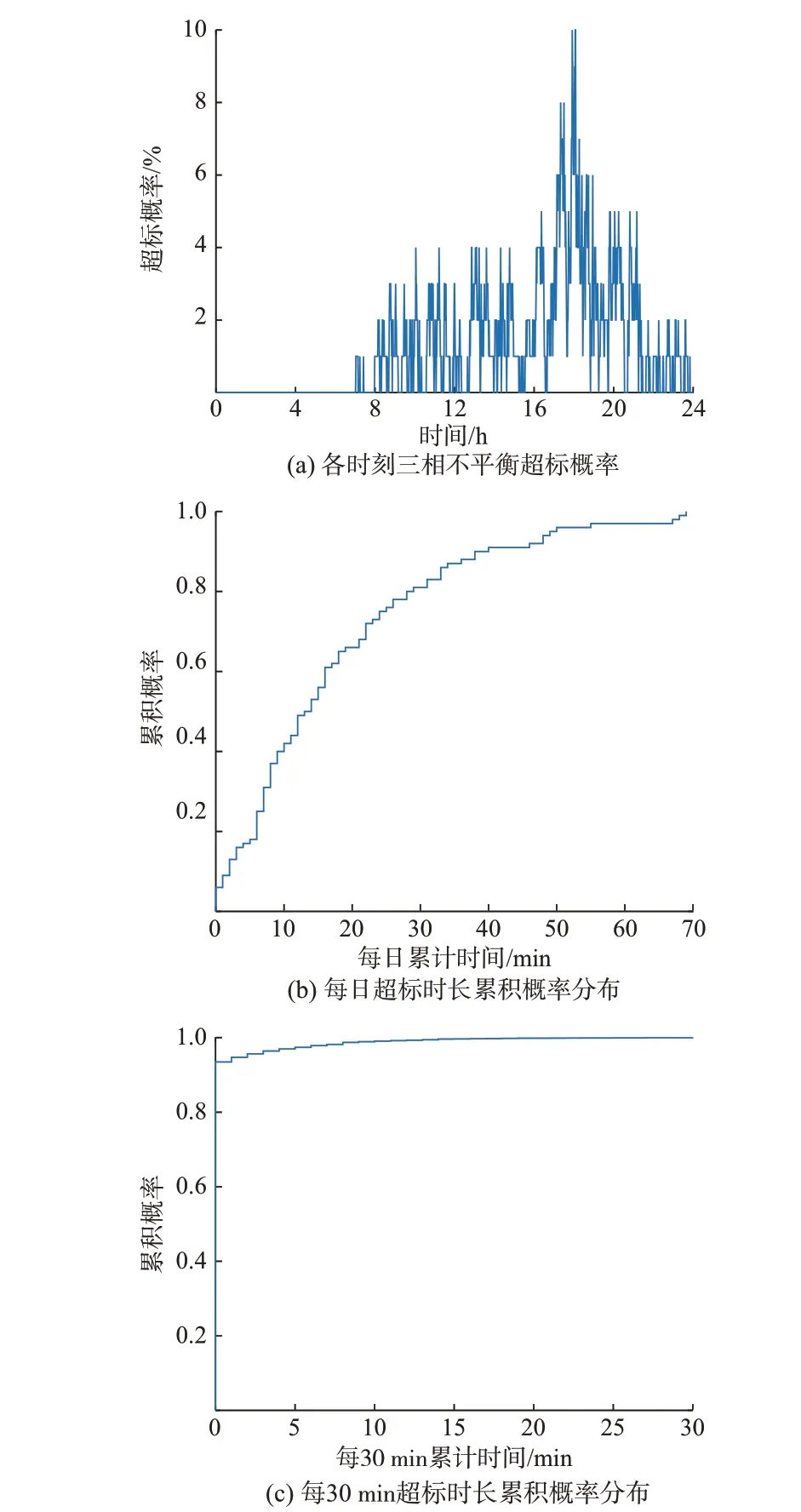
图4 未安装光伏下配电网末节点超标概率Fig.4 Exceeding standard probability at the end node of distribution network without installed photovoltaic

由图4（a）可以看出,末节点24 处三相不平衡超标主要发生在上班前的早晨、中午、傍晚以及深夜这几个时间段,尤其是傍晚超标概率比较严重。可能原因是该时间段居民处于下班到家的状态,用电随机性更大,增大了超标概率。本文方法能够在分钟级精度上分析居民负荷对配电网电能质量的影响,更加细化了配电网三相不平衡超标严重程度。

GB/T 15543—2008《电能质量 三相电压不平衡》指出［32］,日波动三相不平衡可按时间取值:日累计大于2%的时间不超过72 min,且每30 min 大于2%的时间不超过5 min。由图4（b）可以看出,三相不平衡度日累计超标时长并未超过国家标准规定。由图4（c）可以看出,三相不平衡度每30 min有一定概率超过5 min,达到国家规定值。

采用负荷随机时序模型得到的配电网三相不平衡各时刻超标概率、长时间日累计和短时间30 min累计超标时长等指标来表征居民随机用电行为导致低压配电网三相不平衡的严重程度,从而体现配电网节点电能质量不同时刻超标概率,以及配电网节点电压长、短时间尺度累计超标概率。

4.3 光伏容量与渗透率影响分析

光伏出力受光照影响,波动较强,其接入低压配电网,增加了三相不平衡波动的复杂程度。本文在光伏接入位置未知的情况下按均匀分布的方式从各节点及相别中选取接入点,进行1 000 次实验模拟来研究光伏接入对配电网三相不平衡的影响。分别针对光伏相同额定容量和不同额定容量并网情况,对不同渗透率的配电网进行多场景分析。本文定义光伏渗透率为光伏安装容量与变压器额定容量的比值,其中变压器额定容量为80 kV·A。

4.3.1 相同容量光伏接入场景分析

实际工程中,农村居民安装光伏主要受其主观意愿影响,接入位置具有很强随机性,故对光伏接入节点和相位进行随机分配,从而确定配电网光伏配置信息。基于光伏接入数量来分析光伏渗透率与配电网末端节点24 处电压不平衡关系。以额定容量1 kW 的光伏接入为例,构建三相不平衡超标时长累积概率分布图如图5（a）至图5（c）所示。其中图5 中0～50%为光伏渗透率水平,40%均匀接入为40%渗透率水平下在三相线路近似位置均匀接入光伏。

从图5 可以看出,随着光伏渗透率增大,三相不平衡度超标概率逐渐增加。当渗透率超过30%时,由图5（b）和图5（c）分别可以看出,每30 min 和日累计的三相不平衡度超标时长均明显增加,尤其是在该渗透率超过40%时,日累计超标时长大于50%的概率超过国家标准允许值。而对比40%渗透率下光伏随机接入和三相均匀接入对末节点的影响发现,均匀接入降低了三相不平衡度的超标概率。综上,本文从分钟级的角度讨论了光伏接入后配电网三相不平衡度超标情况,从累积概率分布角度分析了相同容量光伏接入配电网对末节点电压电能质量的影响。针对每日累计超标时长和每30 min 超标时长,由光伏渗透率对比结果可知,三相不平衡度超标概率在随机接入光伏情况下会随着渗透率增大而增大,而在相似三相线路均匀接入光伏情况下可以改善由于光伏渗透率增大引起的三相不平衡情况。这也体现了本文方法能从定量角度细化分析光伏接入配电网所带来的影响。

图5 不同光伏渗透率下多指标累积概率分布Fig.5 Cumulative probability distribution of multiple indices with different photovoltaic penetration levels

4.3.2 不同光伏容量安装情况分析

在实际工程中,配电网光伏安装受居民意愿影响很难保证容量相同。考虑户用光伏逆变器容量配置情况,设置配电网的光伏接入容量分别为1、3、5 kW,从光伏安装数量和容量方面评估其对末端三相不平衡的影响程度。在考虑40%光伏渗透率情况下,不同居民光伏安装容量对配电网末节点电能质量的影响如图6所示。其中图6（a）为三相不平衡度每30 min累计超标时长的累积概率分布；图6（b）为三相不平衡度日累计超标时长累积概率分布。

由图6 可以看出,光伏安装容量和光伏渗透率均会影响原居民配电网三相不平衡的超标时长。较低渗透率的光伏接入可以降低三相不平衡度超标时长,但较高渗透率的光伏接入会使该超标时长严重增加。从图6 还可以看出,随着渗透率水平逐步增加,降低光伏安装容量能够减小超标概率。由图6（a）可以看出,居民5 kW 容量配置情况下的三相不平衡度每30 min 累计超标时长超标概率约为0.2,但由图6（b）可以看出,三相不平衡度日累计超标时长的超标概率已经达到0.7,由此可知高渗透率的光伏接入配电网会导致长时间累计超标概率更大。由图6（b）可以看出,在相同渗透率水平下,长时间累计超标概率在混合3 种额定容量的光伏接入配电网情况下大于同一种额定容量的光伏接入配电网情况,并且产生的危害可能会更大。由不同额定容量的光伏接入配电网的结果可知,本文方法能够在分钟级尺度上分析不同光伏接入对配电网电能质量的影响。

图6 40%光伏渗透率下的超标累积概率分布Fig.6 Distribution of cumulative exceeding standard probability with 40% photovoltaic penetration level

5 结语

针对配电网单相设备运行随机不确定性加重配电网三相不平衡的问题,本文提出一种用电数据驱动的低压配电网负荷随机建模及不平衡评估方法,并通过仿真验证了该方法的准确性,得到以下结论:

1）利用高斯混合分布,结合期望最大化算法描述居民用电行为状态。利用Beta 分布及云层覆盖指标描述光伏出力行为状态。通过建立用户用电和光伏出力行为状态模型能够反映多场景下用电设备用电特性的时空概率分布。

2）利用马尔可夫链挖掘居民用电和光伏出力历史数据,建立系统状态转移矩阵,结合序贯蒙特卡洛模拟方法对该状态的持续时间进行抽样,并建立系统用电状态随机模型。该模型描述了用电设备不同时刻用电行为状态之间的联系,能够体现设备用电状态时长及状态变化概率。

3）利用LHS 技术将所提负荷随机模型与配电网潮流计算相结合,分析了配电网末端三相不平衡变化情况,结果更接近配电网实际情况。从多时间尺度的累计超标时长角度分析三相不平衡超标情况,能够从分钟级角度实现对配电网三相不平衡超标概率评估,并为配电网规划等相关人员提供参考。

本文尚未针对典型场景数据量以及配电网不对称结构进行研究。在后续的研究中,将进一步改进模型,以便扩展其应用范围。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。