基于改进雨流计数法的梯次利用电池储能系统优化控制
王育飞,叶俊斌,薛 花,米 阳
(上海电力大学电气工程学院,上海市 200090)
0 引言
近年来,中国电动汽车保有量持续增长,动力电池需求量也随之不断增加。研究表明,动力电池容量衰减至80%左右时需作退役处理,否则无法满足电动汽车正常行驶要求[1]。据推算,中国首个动力电池退役高峰期即将来临,预计2030 年退役总量将超过7×105t[2]。因此,亟须建立退役电池梯次利用体系,加快环境友好型、节约型产业结构发展。以退役电池为储能单元,构建梯次利用电池储能系统是推进退役电池梯次利用的有效路径[3]。目前梯次利用电池储能系统相关研究主要包括拓扑结构设计[4]、典型场景应用[5-6]、容量配置规划[7]及控制策略改进[8]等方面。其中,梯次利用电池储能系统控制策略设计与梯次利用电池运行效率及运行寿命密切相关,对降低梯次利用电池储能系统运行成本具有重要意义。
梯次利用电池历史运行工况复杂,梯次利用电池储能系统各储能单元的健康状态(state of health,SOH)通常存在较大差异[9]。因此,梯次利用电池储能系统运行时需对不同储能单元进行差异化功率分配,以克服“短板效应”,提高整体运行效率[10]。现有关于电池储能系统功率分配策略的研究已取得一定成果,但少有专门针对梯次利用电池储能系统的相关控制策略研究。文献[11-12]结合具体应用场景进行储能系统各时刻功率分配建模,优化各储能单元的荷电状态(state of charge,SOC)均衡度;文献[13]计及各储能单元的SOH 差异性进行功率分配,实现“新电池深充深放,旧电池浅充浅放”的优化分配目标;文献[14-15]基于充放电任务分组执行的功率分配模式,降低各储能单元充放电切换次数,延长电池使用寿命;文献[16]进一步提出储能单元分组优化策略,使充电组和放电组的储能单元可在系统调节能力不足时进行动态转换,提高储能系统功率调节能力。综上,电池储能系统功率分配策略主要存在整体控制和分段控制2 种模式,整体控制模式根据控制目标将各时刻充放电功率需求按指定策略分配至每一储能单元,在功率需求不为零的时刻,各储能单元均处于工作状态;分段控制模式通过对储能单元进行分组,使各储能单元分时段进行不同类型的能量响应,通常情况下仅部分储能单元处于运行状态。
梯次利用电池储能系统各储能单元的个体差异较大,若采用整体控制模式进行功率分配,需对每一梯次利用电池进行变流器配置,以实现同一时刻对各储能单元充放电功率的独立控制,将极大增加退役电池梯次利用成本。若采用分段控制模式进行梯次利用电池储能系统功率分配,通过选取不同SOH的梯次利用电池或电池组合对不同时段、不同大小的能量需求进行分级响应,可降低变流器配置成本,还能实现不同梯次利用电池的差异化控制,提高梯次利用电池储能系统运行安全性与可靠性。然而,由于储能系统多用于平抑可再生能源或随机负荷波动,各时段充放电量需求存在较大不确定性,为确保各时段投入运行的梯次利用电池具有充足的可用容量进行能量响应,梯次利用电池储能系统分段控制过程需依赖高精度SOC 估算技术进行梯次利用电池的SOC 动态更新,而该技术在现阶段工程应用中仍较难实现。
雨流计数法(rain-flow counting algorithm,RCA)是工程界广泛用于材料疲劳寿命分析的一种计算方法,现储能领域中多利用RCA 将电池SOC变化历程分解为多段充放电循环过程,通过计算各循环过程的等效全循环次数,估算电池循环寿命[17]。梯次利用电池储能系统分段控制过程中,可利用RCA 将储能系统能量需求分为多段充放电量相等、容量需求各异的循环过程,采用不同SOH 的梯次利用电池对不同容量需求的循环过程进行分级响应。由于各循环过程的充放电量相等,参与能量响应的梯次利用电池均能在各时段末恢复至初始SOC,降低了分段控制过程对各储能单元的SOC 估算精度要求。
鉴于以上分析,本文以光储充电站为退役电池梯次利用场景,建立储能系统分段能量需求模型;设计梯次利用电池储能系统分段控制模式,采用RCA 对该模式进行优化,并针对RCA用于梯次利用电池储能系统分段控制时存在的时序丢失和区间重叠问题对传统RCA 进行改进,提出基于改进RCA 的梯次利用电池储能系统分段控制策略;通过算例分析验证所提梯次利用电池储能系统分段控制策略的有效性。
1 储能系统分段能量需求模型
中小型电动汽车充电站的储能系统能量需求与梯次利用电池额定参数较为接近,且光伏发电系统的接入可进一步降低充电站负荷调峰需求,减小分段控制过程中梯次利用电池串并联运行规模,降低梯次利用电池储能系统运行损耗[18]。因此,选取光储充电站为研究对象,进行储能系统分段能量需求建模。
设计的光储充电站拓扑结构及其功率流向见附录A 图A1。根据能量守恒原理,光储充电站在任意时刻t满足功率平衡等式:
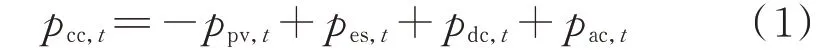
式中:pcc,t为t时刻并网功率;ppv,t、pes,t、pdc,t、pac,t分别为t时刻光伏发电系统、梯次利用电池储能系统、直流充电系统和交流充电系统传输功率,其中pes,t以充电为正、放电为负。

式中:t0为起始计量时刻。
根据式(9),可得储能系统第i个时段(i=

2 梯次利用电池储能系统分段控制策略
光储充电站不同时段的光伏出力和充电负荷均存在一定差异,因此储能系统在不同时段具有不同的充放电能量需求。与此同时,不同SOH 梯次利用电池的充放电能力也存在一定差异,合理选取梯次利用电池或电池组合进行储能系统分段能量响应,既可保证光储充电站并网功率调节效果,又能克服“短板效应”,提高梯次利用电池储能系统运行效率。
2.1 动力电池充放电能力衰减特性分析
SOH 是衡量电池寿命阶段的重要指标,现有研究多采用容量保持率进行SOH 表征[3]。容量保持率越大,SOH 较优,表明电池充放电能力越强;容量保持率越小,SOH 较差,表明电池充放电能力越弱。以电动汽车三元锂动力电池为例,其最大可用容量与等效全循环次数满足式(10)[19]。
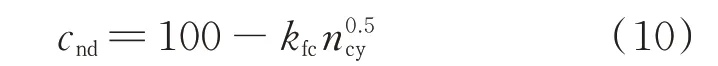
式中:cnd为动力电池老化过程中的归一化最大可用容量;ncy为等效全循环次数;kfc为容量衰减系数,与温度、放电深度(depth of discharge,DOD)和充放电切换频率等因素有关。由式(10)可知,随着循环次数的增加,动力电池最大可用容量逐步减小,充放电能力逐步衰退。
2.2 梯次利用电池储能系统分段控制模式设计
受车主驾驶习惯、驾驶环境等因素影响,动力电池初始退役时老化程度不一,其容量保持率在70%~80%的区间内呈现一定分散性[20]。退役电池梯次利用过程中,由于不同电池的DOD 和充放电切换频率相差较大,梯次利用电池储能系统中各梯次利用电池的容量保持率差距进一步拉大,不同电池间的充放电能力差异凸显。为避免对SOH 较差梯次利用电池进行深充深放,同时发挥SOH 较优梯次利用电池的充放电能力,在储能系统容量需求较大的时段宜采用SOH 较优梯次利用电池进行能量响应,而在储能系统容量需求较小的时段可采用SOH 较差梯次利用电池投入运行。基于上述分析,提出梯次利用电池储能系统分段控制模式,步骤如下。
1)时间分段
考虑储能系统分段能量需求与梯次利用电池最大可用容量的匹配性,确定储能系统分段时刻τ1~τNT(NT为分段时刻数),将储能系统运行过程分为多个连续时段T1~TNT-1。其中Ti=(τi,τi+1],满足式(11)所示约束条件。

式中:fP{θ}为事件θ发生的概率;λc为容量冗余系数;NB为梯次利用电池配置总数;cbat,k为梯次利用电池k的最大可用容量(k=1,2,…,NB);εM为容量需求越限时段最高允许占比;εm为低容量需求时段所需达到的最低占比;Δτmin为梯次利用电池储能系统允许的最短切换时间;τi为第i个分段时刻。
2)储能运行需求计算
根据式(9),计算最大功率需求向量Pdm及最大容量需求向量Edm如式(12)所示。

式中:ndm,i和cdm,i分别为时段Ti投入的电池数目和电池容量需求;fceil(·)为向上取整函数;plim为单组电池的最大功率限值;λn为电池数目冗余系数。
3)电池响应方案选择
结合式(14)所示约束条件,选择各时段参与储能系统能量响应的梯次利用电池或电池组合K,得到各时段的电池响应方案。
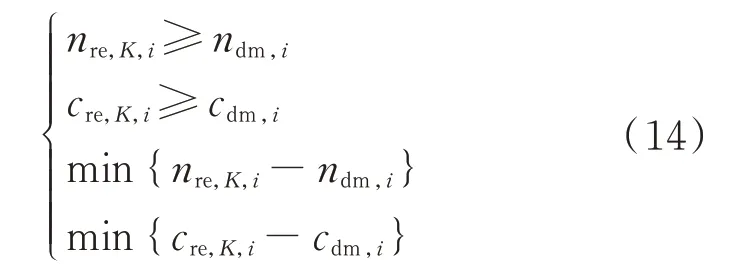
式中:nre,K,i和cre,K,i分别为梯次利用电池组合K在时段Ti的电池数目及实时可用容量。其中,cre,K,i满足式(15)所示关系。
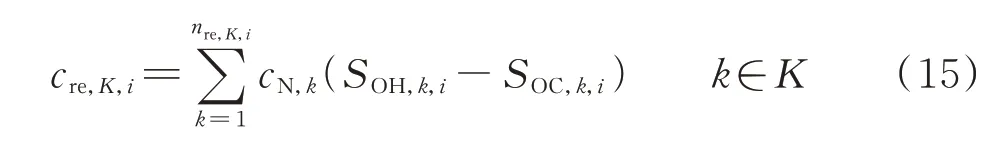
式中:cN,k为梯次利用电池k的额定容量;SOH,k,i和SOC,k,i分别为梯次利用电池k在时段Ti起始时刻的SOH 值和SOC 值,其中SOH 值为梯次利用电池充满时以标准倍率放电至截止电压所放出的电量与其标称容量的比值,SOC 值为梯次利用电池剩余可放电量与其标称容量的比值[3]。
由式(15)可知,为保证光储充电站并网功率调节达到预期效果,梯次利用电池储能系统运行时需在每一时段末更新各梯次利用电池或电池组合的实时SOH 和SOC,以保证参与分段能量响应的梯次利用电池或电池组合具有充足的可用容量。其中,SOH 作为电池全生命周期运行寿命的一项衡量指标,在时间尺度较短的储能系统分段控制过程中可近似认为恒定不变;SOC 在储能系统分段控制过程中则随电池充放电功率动态变化。因此,储能系统分段控制对电池SOC 估算精度要求较高,但目前常用的安时积分法、卡尔曼滤波法和神经网络算法均存在不同程度的SOC 估算误差[21],且由于梯次利用电池的运行工况相比于常规储能电池更加复杂,使SOC 精确估算的难度进一步增大,而SOC 估算误差易导致电池实际可用容量无法满足所在时段能量需求的情况,影响梯次利用电池储能系统控制效果。
2.3 梯次利用电池储能系统分段控制策略优化
为解决SOC 估算误差给梯次利用电池储能系统控制带来的不确定性问题,本文采用RCA 对梯次利用电池储能系统分段控制流程进行优化。具体思路如下:

3)在各循环过程的运行区间中,选择不同SOH的梯次利用电池或电池组合对不同容量需求的循环过程进行分级响应,使梯次利用电池在参与各循环过程能量响应后能够恢复至初始SOC。
传统RCA 在寿命分析领域应用中无须关注载荷历程的时序信息,在参数提取过程中仅保留了各循环过程的变化幅值,不适用于对上述优化思路进行具体设计,因此需对传统RCA 做出改进。
2.3.1 改进RCA
如图1 所示,RCA 用于解决储能系统分段控制问题时,除提取循环过程的纵向变化幅度(d1、d2)外,还需在计数过程中保留各循环过程两端的时间信息(τ1、τ2、τ3、τ4)作为时间分段操作的分界时刻;此外,不同循环过程可能存在区间重叠的现象,如图1中红色区域循环过程所属时间区间包含于蓝色区域循环过程所属时间区间中,使后者被分割为两段或多段不同区间。储能系统分段控制时,需对被分割区间进行关联,使同一循环过程中不同时段参与储能系统能量响应的梯次利用电池或电池组合保持一致,避免出现充放电量不均衡的情况。
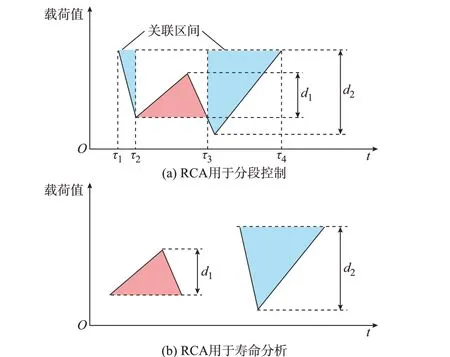
图1 不同应用模式下RCA 所需提取参数对比Fig.1 Comparison of extraction parameters required by RCA in different application modes
针对上述问题,基于RCA 的“三变程”计数原则[22],提出用于储能系统分段控制优化的改进RCA如图2 所示,图中:iL和ied分别为参数提取条件判断和结束时刻计算的中间变量。主要包括以下步骤。
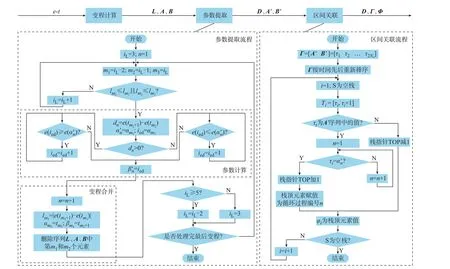
图2 用于梯次利用电池储能系统分段控制策略优化的改进RCA 原理图Fig.2 Schematic diagram of improved RCA for segmented control strategy optimization of energy storage system with echelon utilization batteries
1)变程计算
提取能量-时间变化曲线(e-t)过程中所有极值点和两端边界点,得到由各点时刻信息按时间先后构成的时间向量t如式(16)所示。

式中:lm(m=1,2,…,Ne-1)为第m变程大小;αm和βm分别为第m变程的起始时刻和结束时刻;e(t)为曲线e-t在t时刻对应的能量值。
2)参数提取
依次取出变程向量L中3 个连续变程lm1、lm2、lm3,并作以下判断。
(1)若满足提取条件lm2≤lm1且lm2≤lm3,则提取为一循环过程,记为ζn(n=1,2,…),并计算循环过程ζn的能量变化幅度dn及起始时刻α′n、结束时刻β′n。其中,dn、α′n可根据式(18)得出:
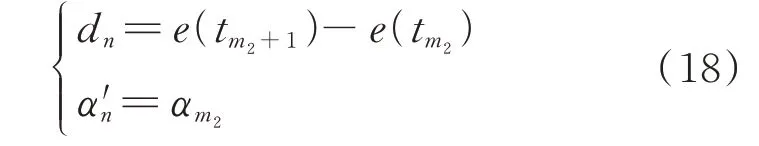
结合图2 所示参数计算流程,根据以下操作得到循环过程ζn的结束时刻β′n。
若dn>0,表示ζn为“先充后放”循环过程,则由α′n的下一时刻开始向后推移,逐一计算各时刻能量净值,直至第1 次出现某时刻能量净值不大于α′n时刻的能量净值,记录该时刻为β′n。
若dn≤0,表示ζn为“先放后充”循环过程,则由α′n的下一时刻开始向后推移,逐一计算各时刻能量净值,直至第1 次出现某时刻能量净值不小于α′n时刻的能量净值,记录该时刻为β′n。
循环过程ζn的相关参数dn、α′n、β′n提取完毕后,结合图2 所示变程合并流程,将第m1和m3变程合并为新的m3变程,删去m1和m2变程,更新变程向量L,在新的向量L中重复上述判断。
(2)若不满足提取条件lm2≤lm1且lm2≤lm3,则在向量L中以m2和m3变程为基础继续向后读取一变程作上述判断,直至处理完最后一变程。
通过上述操作,可将能量变化过程曲线e-t分为循环过程ζ1~ζNc(Nc为循环过程数),得到式(19)所示能量变化幅度向量D、起始时刻向量A′和结束时刻向量B′。

相比于传统RCA,改进RCA 除提取了各循环过程的能量变化幅度信息D外,还记录了各循环过程的始末时刻信息A′和B′,以便作为储能系统分段控制过程中的时间分段依据。
(3)区间关联
考虑以循环过程ζ1~ζNc的始末时刻作为能量变化过程曲线e-t的分段时刻,将起始时刻向量A′和结束时刻向量B′合并,按时间先后排列为式(20)所示分段时刻向量Γ,根据Γ将曲线e-t分为时间区间T1~T2Nc-1,其中Ti=(τi,τi+1]。

考虑不同循环过程存在区间重叠现象,若时间区间Ti的左端点为某循环过程的起始时刻,则表示时间区间Ti为一新的循环过程;若时间区间Ti的左端点为循环过程的结束时刻,则需结束当前循环过程并恢复为上一未结束的循环过程。
为建立同一循环过程中不同时间区间的关联性,结合计算机领域的进/出栈算法,设计图2 所示区间关联流程:对任意时间区间Ti,当τi=α′n时执行进栈操作,使栈顶指针加1,栈顶元素赋值为循环过程编号n;当τi=β′n时执行出栈操作,使栈顶指针减1,栈顶元素恢复为上一未结束的循环过程编号。读取各时间区间的栈顶值,可得到式(21)所示关联标识向量Φ。
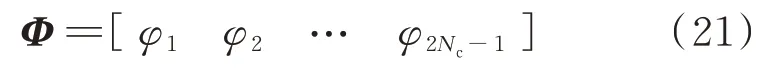
式中:φi为时间区间Ti的关联标识,当φi=n时,表明时间区间Ti为循环过程ζn的对应工作时段。
综上,改进RCA 不仅保留了各循环过程两端时刻信息,而且利用进/出栈算法得到各时间区间的关联标识,将同一循环过程的多个时间区间通过该标识相互关联,使各梯次利用电池均可完整参与循环过程响应,实现能量自平衡。
2.3.2 梯次利用电池储能系统分段控制策略优化
基于改进RCA 的梯次利用电池储能系统分段控制策略优化如图3 所示,主要包括以下步骤。
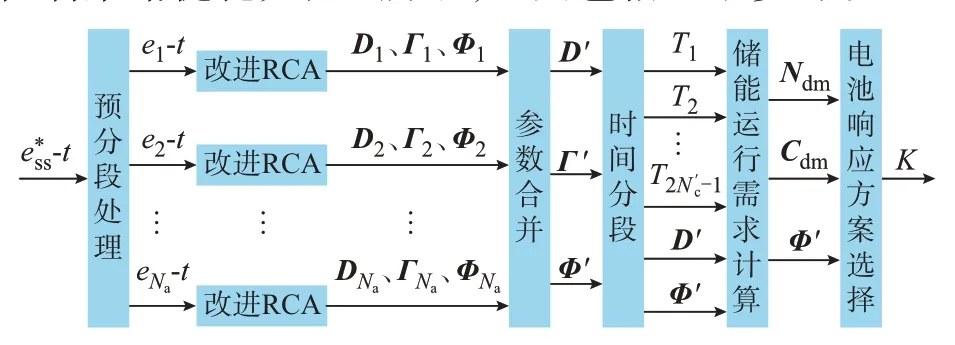
图3 基于改进RCA 的梯次利用电池储能系统分段控制流程Fig.3 Segmented control flow of energy storage system with echelon utilization batteries based on improved RCA
1)预分段处理


将Φj(j=1,2,…,Na)中所有元素合并为同一向量。为避免不同预分段曲线的关联标识重复,对于Φj(j>1)中每一元素值,在其原有值的基础上叠加数值max {Φj-1},进行关联标识修正,得到整个工作区间的关联标识向量Φ′如式(24)所示:

参照式(13)进行各循环过程电池数目需求向量Ndm和电池容量需求向量Cdm计算,结合式(14)所示约束条件得到各循环过程参与能量响应的梯次利用电池或电池组合K。对于任意时段T′i,若φ′i=n,则选取循环过程ζ′n对应的梯次利用电池或电池组合K进行储能系统分段能量响应。
3 算例分析
3.1 数据选取与参数设定
为了验证所提梯次利用电池储能系统分段控制策略的有效性,基于MATLAB 仿真平台,选取中国上海某光储充电站的24 h 光伏出力、充电负荷运行数据及原搭载于荣威MARVEL X 的退役三元锂动力电池进行仿真分析。其中,光储充电站运行曲线见附录A 图A2,动力电池额定容量为52.5 kW·h,电池退役前的最大放电功率为222 kW。
该充电站配置有4 台30 kW 直流充电桩和14 台3.5 kW 交流充电桩,光伏装机容量为40 kW,通过1 台150 kV·A 变压器接入配电网。该充电站原配有150 kW/150 kW·h 电池储能系统,目前每千瓦时常规储能装置成本约为梯次利用电池的2~3 倍[14],相同成本最多可配置约300 kW·h~450 kW·h 梯次利用电池。综合考虑电池管理系统和消防安全设备升级[24],以及所提梯次利用电池储能系统分段控制策略的技术特点,配置储能系统为6 组SOH 值分别为0.55、0.60、0.65、0.70、0.75、0.80 的梯次利用电池,总额定容量为315 kW·h,并进行以下设定。
1)参照文献[16],设定光储充电站并网功率平滑系数tps为15 min。
2)根据现行国家标准GB/T 13462—2008[25],考虑变压器经济运行,设定并网功率上限为变压器容量的75%,即pcc,M=112.5 kW。
3)为避免充电站向电网倒送电能,需保证并网功率大于零。考虑保留适当安全裕度,设定并网功率下限为变压器容量的1%,即pcc,m=1.5 kW。
4)考虑梯次利用电池运行的安全性及可靠性,设定单组梯次利用电池的最大功率限值plim为电池退役前最大放电功率的50%,即plim=111 kW。
3.2 仿真结果与分析

3.2.1 控制策略验证
根据2.3.2 节所述步骤,首先对储能系统净能量

为结合不同循环过程的容量需求差异对退役电池进行分级利用,根据所得向量D′将循环过程分为“先充后放”(d′n>0)和“先放后充”(d′n≤0)两类,分别按各循环过程的最大容量需求edm对两类循环过程进行排序,结果见附录A 图A6,可知各循环过程的电池容量需求存在分级差异。采用K-means 算法分别对两类循环过程进行聚类,进一步将容量需求分为6 类,确定6 组梯次利用电池参与分段能量响应的容量临界值如表1 所示。
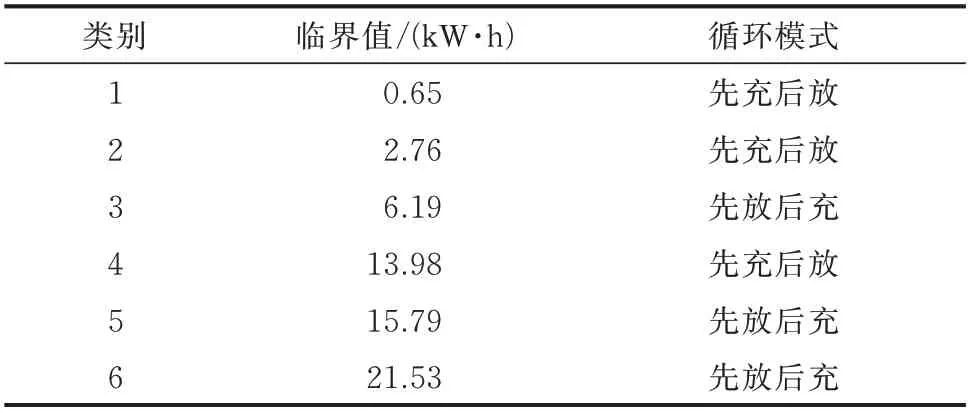
表1 各循环过程的电池容量需求分级Table 1 Classification of battery capacity requirements for each cycle
采用SOH 由小到大的6 组梯次利用电池对由低到高的6 类容量需求进行分级响应。考虑“先充后放”循环过程无须进行初始电能储备,将SOH 为0.55、0.60、0.70 的3 组梯次利用电池初始SOC 设定为0.1;反之,由于“先放后充”循环过程需在初始时预留有充足电量,针对SOH 为0.65、0.75、0.80 的3 组梯次利用电池,设定其初始电量为最大可用容量的90%。基于此设定,得到所提控制策略下各梯次利用电池的SOC 变化曲线如图4 所示。其中,SOH表示梯次利用电池SOH 值。
由图4 可知,所提控制策略下各梯次利用电池在进行每一循环过程的能量响应后可恢复至初始SOC,实现各阶段电池内部充放电能量自平衡,避免了储能系统分段控制过程中由于SOC 估算误差造成的电池充放电能力不足问题;同时,所提控制策略结合不同循环过程的容量需求进行梯次利用电池投运,实现了“新电池深充深放,旧电池浅充浅放”的优化运行目标;此外,6 组梯次利用电池交替参与储能系统分段能量响应,避免了“短板效应”使电池能量利用率低下的问题。
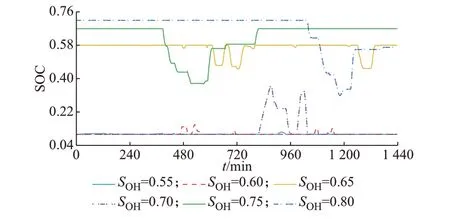
图4 所提控制策略下各梯次利用电池的SOC 变化曲线Fig.4 SOC change curves of each echelon utilization battery with proposed control strategy
3.2.2 控制效果对比
为验证所提控制策略在提升梯次利用电池储能系统控制效果方面的优势,选取工程领域中常用的功率均分策略及学术领域中常见的比例分配策略、分组控制策略用于梯次利用电池储能系统控制策略设计,并与所提控制策略进行对比分析。其中,功率均分策略将储能系统各时刻的功率需求均分至每一电池,比例分配策略根据电池可用容量占比进行各时刻功率分配,两者同属整体控制模式;分组控制策略将电池分为充电组和放电组,分别执行充、放电任务,直至电池SOC 达到临界值,进行充放电分组转换,与所提控制策略同属分段控制模式。3 种对比方案下各梯次利用电池的SOC 变化曲线见附录A图A7。
参照文献[26]可知,DOD、充放电切换次数和静置情况是影响电池运行效率和运行寿命的主要技术指标,因此采用以上3 种指标对不同控制策略下的梯次利用电池储能系统运行性能进行对比分析。
1)DOD 对比
梯次利用电池储能系统中各梯次利用电池的SOH 存在较大差异,宜采用“新电池深充深放,旧电池浅充浅放”的分级控制模式对其进行能量管理。不同控制策略下各梯次利用电池最大DOD 如图5所示。由图5 可知,功率均分策略下各梯次利用电池DOD 处于较低水平,可延缓SOH 较差梯次利用电池的寿命衰减,但限制了SOH 较优梯次利用电池的充放电能力;分组控制策略下各梯次利用电池的DOD 则保持于较高水平,使SOH 较差梯次利用电池工作于深充深放模式,影响梯次利用电池储能系统运行安全性及可靠性,不宜用于梯次利用电池储能系统控制策略设计。

图5 不同控制策略下各梯次利用电池的最大DOD 对比Fig.5 Maximum DOD comparison of each echelon utilization battery with different control strategies
比例分配策略和所提控制策略均具备“新电池深充深放,旧电池浅充浅放”的控制效果。如对于SOH 为0.55 和0.60 的梯次利用电池,比例分配策略下的DOD 分别为功率均分策略的81.37% 和88.82%,所提控制策略下的DOD 分别为功率均分策略的11.00%和46.67%,两者均使SOH 较差电池处于较低强度的工作状态;对于SOH 为0.75 和0.80的梯次利用电池,比例分配策略下的DOD 分别为功率均分策略的111.01%和118.37%,所提控制策略下的DOD 分别为功率均分策略的266.90% 和363.89%,且DOD 最大值仅为0.41,两者均在保证安全运行的前提下充分发挥了SOH 较优梯次利用电池的充放电能力。相比于比例分配策略,所提控制策略的分级控制效果更加显著,因此所提控制策略可有效提升梯次利用电池储能系统的分级控制效果。
2)充放电切换次数、静置情况对比
由于电池的极化作用,电池电压在电流方向或电流大小发生变化时存在一定的迟滞效应,频繁进行电池充放电状态切换或调节充放电功率将增加电池运行损耗。不同控制策略下各梯次利用电池的充放电切换次数、静置时段数和平均静置时间如表2所示。由表2 可知,功率均分策略和比例分配策略下,梯次利用电池在储能系统功率需求不为零的各时刻均处于工作状态,24 h 内各梯次利用电池的充放电切换高达101 次,不存在静置时间。分组控制策略则在降低梯次利用电池充放电切换次数方面具有较强优势,24 h 内存在较多的静置时段及一定的静置时间,但各梯次利用电池的DOD 过大,限制了其在梯次利用电池储能系统控制策略设计中的应用。所提控制策略下,梯次利用电池充放电切换次数最高仅为功率均分策略和比例分配策略的52.48%,相邻两循环过程间存在平均30 min 以上的静置时间,相比于功率均分策略和比例分配策略有较大改善。因此,所提控制策略可有效提高电池充放电效率,减小梯次利用电池储能系统运行损耗。
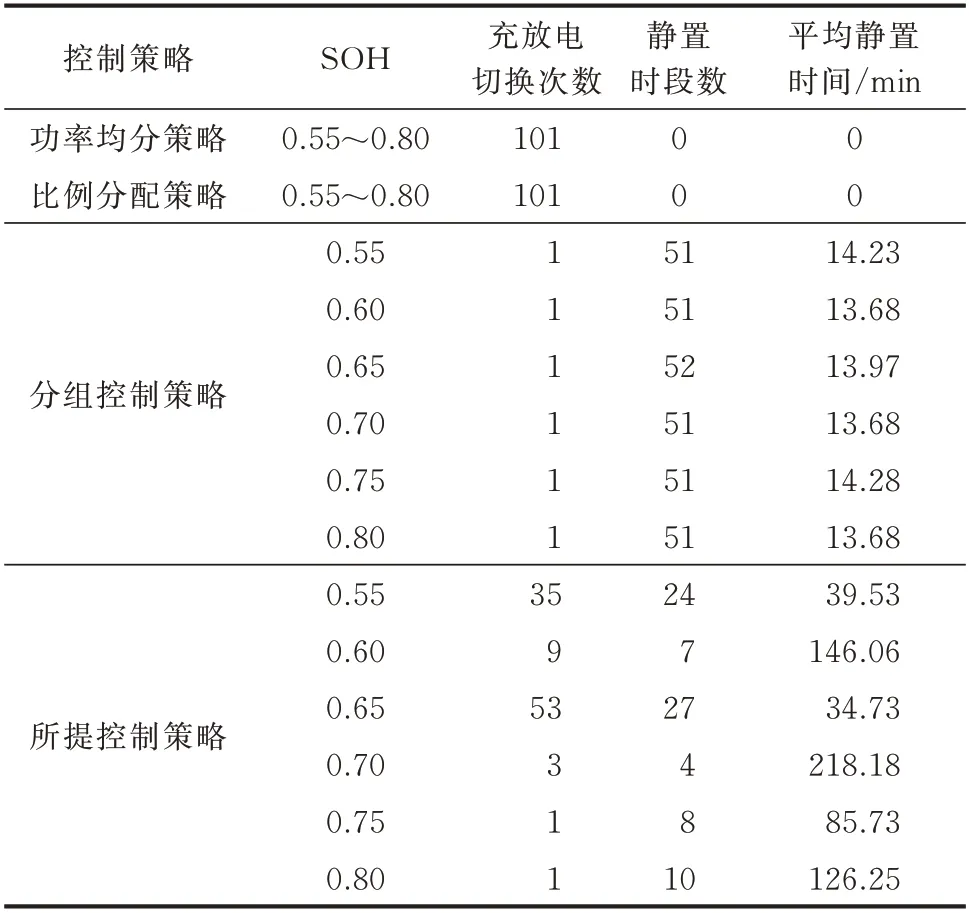
表2 充放电切换次数和静置情况对比Table 2 Comparison of charging and discharging switching and standing situation
3)综合性能分析
相较于3 种对比方案,所提控制策略在协调分配梯次利用电池储能系统中各梯次利用电池DOD和充放电切换次数方面具有独特的性能优势。结合图5 和表2 可知,所提控制策略下SOH 较差梯次利用电池的充放电切换次数虽比SOH 较优的梯次利用电池稍高,但其始终处于浅充浅放的运行状态,且相邻循环过程之间存在一定的静置时间,具有较充裕的容量和时间消除电池极化作用对控制效果的影响,进一步降低了梯次利用电池运行损耗;SOH 较优梯次利用电池的DOD 虽比SOH 较差梯次利用电池稍大,但其充放电切换频率较低,且在充放电过程中存在较多、较长的静置时段,如SOH 为0.80 的梯次利用电池的DOD 虽达到了0.41,但其在24 h 运行过程中仅进行了一次充放电切换,且其中存在10 个静置时段,平均静置时长达到126.25 min,保证了深度充放电过程的稳定运行。因此,所提控制策略可结合梯次利用电池SOH 特性优化梯次利用电池储能系统功率分配,有效提升了梯次利用电池储能系统的控制效果。
4 结语
针对梯次利用电池储能系统优化控制问题,以光储充电站为退役电池梯次利用场景,提出基于改进RCA 的梯次利用电池储能系统分段控制策略,并利用MATLAB 仿真平台进行算例分析,得出以下结论。
1)所提梯次利用电池储能系统分段控制策略实现了各阶段电池能量自平衡,避免了梯次利用电池储能系统分段控制过程对高精度SOC 估算的过度依赖,提高了梯次利用电池储能系统运行可靠性。
2)所提梯次利用电池储能系统分段控制策略下,6 组SOH 由小到大的梯次利用电池DOD 分别为功率均分策略的11.00%、46.67%、104.61%、236.29%、266.90%、363.89%,DOD 最大值仅为0.41,在保证安全运行的前提下,实现了“新电池深充深放,旧电池浅充浅放”的退役电池分级利用目标。
3)所提梯次利用电池储能系统分段控制策略下,各梯次利用电池的充放电切换次数最高仅为功率均分策略和比例分配策略的52.48%,且充放电切换过程主要集中于浅充浅放、应变容量空间较大的梯次利用电池组,各循环过程间存在平均30 min 以上的静置时间,降低了充放电切换产生的运行损耗。
4)所提梯次利用电池储能系统分段控制策略下,SOH 为0.70、0.75、0.80 的梯次利用电池DOD 较大,但其24 h 内充放电切换次数不超过3 次,且运行过程中存在不少于4 段、平均80 min 以上的静置时段,保证了深度充放电过程稳定运行,充分发挥了SOH 较优梯次利用电池的深度充放电能力。
所提梯次利用电池储能系统分段控制策略具有一定工程参考价值,后续研究将结合不同SOH 梯次利用电池的运行特性,对DOD、充放电切换次数、静置时长及静置时段分布等因素进行定量优化,进一步提升梯次利用电池储能系统控制效果。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

