基于深度学习的心血管血流动力学参数反演

周 阳 潘 怡 崔 畅 陈明龙 孙蓓蓓

(1东南大学机械工程学院，南京 211189)(2南京医科大学第一附属医院心血管内科，南京 210029)

血流动力学建模是研究心血管活动的重要技术手段，其通过计算机数值模拟，以一种快速、准确的方式对血液流动现象进行表征和预测[1-2].不同形式的心血管模型已被开发并被用于各种临床场景，如零维模型[3]、一维模型[4]以及三维模型[5]等.零维-一维耦合模型由于能以较低的计算成本准确提供脉搏波形态以及局部位置的压力和速度信息，得到学者们的广泛关注，并已被成功应用于周身循环和局部血流动力学的研究[6].为了提高物理模型的预测精度，根据患者临床实际测量数据对其进行个性化建模尤为重要，相关的参数反演策略已成为心血管血流动力学领域的研究热点[7-8].

目前心血管参数反演方法主要包括参数优化法和滤波法.参数优化法以模型输出与实际测量的差值构建损失函数，并利用牛顿法或LM等算法通过最小化损失函数来求出未知参数.Itu等[9]对基于牛顿法的心血管模型参数反演进行了大量的研究；Zhang等[10]对真实病人的临床数据采用LM算法进行了参数反演实验，研究结果表明个性化模型的输出与实际测量吻合度良好.滤波法是一种动态递归的参数估计方法，基于卡尔曼滤波(KF)原理，利用每个时间步的卡尔曼增益来进行参数迭代更新[11].根据心血管数值模型的特点，学者们相继提出利用降价无迹卡尔曼滤波[12]和集合卡尔曼滤波[13]来求解血流动力学的反问题，并取得了积极的成效.然而，这些方法在实际使用中存在迭代计算量大、初始值设置不合理以及迭代发散等情况，往往需要人工干预来调整初始参数和收敛条件，难以取得明显的效率提升.此外，当存在多个心动周期的测量数据时，上述方法并不能对这些数据进行较好的综合利用.

由于深度学习技术的迅速发展，利用人工神经网络进行非线性映射为参数反演提供了新的思路，并在不同领域的参数反演任务中得到了初步的应用[14].临床测量中常涉及包括离散数值以及连续波形在内的不同形式的数据，传统的神经网络对这些复杂的数据难以取得满意的映射效果.因此，提出一种混合多源输入的深度神经网络(DNN)模型，根据不同类型的测量数据，分别采用卷积神经网络与全连接神经网络来提取其对参数的依赖特征.同时，针对波形噪声的干扰，采用一种集成网络模型来进一步提高参数反演的精度.通过引入一个多尺度血流动力学模型对所提方法进行有效性验证，并讨论了不同水平的噪声对反演精度的影响.

1 多尺度血流动力学模型

建立了一个零维-一维耦合的多尺度心血管血流动力学模型.如图1所示.图中，R0和R分别为末梢血管近端和远端阻力；C为末梢血管的顺应性；T为心动周期；T1为心脏射血时间；Qmax为入口流率最大值；QAV为主动脉入口流率.一维模型用于描述血流在55条动脉内的速度和压力情况，而零维模型则用于描述外周小血管及毛细血管的阻力和顺应性.假设动脉内的血流是黏性不可压缩的，一维模型的控制方程如下[15]：

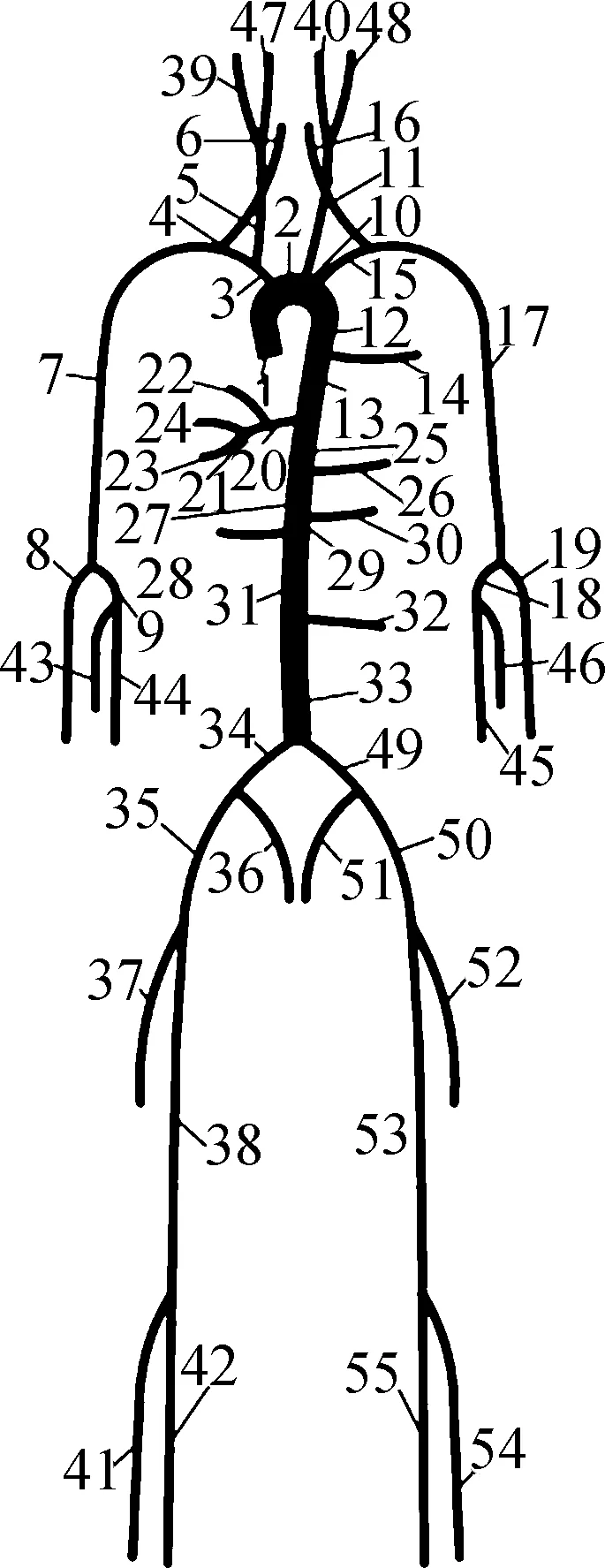
(a)55条动脉示意图

(1)

(2)

式中，t为时间；x为动脉长度方向的坐标；A为血管的横截面积；P为该横截面的平均压力；U为相应的平均流速；Kr为血流的黏性阻力系数，这里将其设为 8πν，其中动力黏度ν为4.43 cm2/s；ρ为血液的密度，其值假定为常数1.06 g/cm3.

采用弹性本构方程来定义血流与动脉壁的耦合关系，即

(3)

(4)

式中，P0为参考压力；A0为压力处于P0时的血管横截面积；β为血管的刚度参数；E和h分别为血管壁的弹性模量和壁厚.模型的主动脉入口流率QAV采用如图1(b)所示的近似流量曲线，其中，Qmax与心脏每搏输出量SV有如下关系[10]：

(5)

出口边界采用一个三元素Windkessel模型来描述血流在末端血管的行为，如图1(c)所示，其控制方程如下：

(6)

式中，Q为血管内截面的平均流量，且有Q=AU.采用Maccormack格式对上述一维模型的双曲偏微分方程进行数值离散[16].根据Zhang等[10]提出的参数估计设置，将55条动脉分为3个集群，如图1(a)所示，其中臂动脉集群包括标号为3、4、7、8、9、15、17、18、19、43、44、45、46的动脉段，颈动脉集群包括标号为5、6、11、16、39、40、47、48 的动脉段，其他动脉段则被归为主动脉集群.分别采用3个缩放系数Cβ_arm、Cβ_car和Cβ_aor对上述3个集群的刚度参数在标称值的基础上进行缩放.采用参数CR用于统一缩放边界阻力R.

模型中涉及的动脉几何参数、刚度以及外周血管参数来自文献[10].执行参数反演所需的临床测量包括心率(RH)、右肱动脉(标号7)、右股动脉(标号38)的压力波形以及右颈动脉(标号5)的血流速度波形.心脏射血时间T1根据测得的心率和已有的回归公式进行计算[17].

2 基于DNN的参数反演模型

2.1 卷积神经网络模型

采用卷积神经网络(CNN)来提取连续生理波形的特征信息，如图2所示.如图2(a)所示，将一维的压力波形W1、W2以及血流波形W3堆叠为一个二维的波形特征矩阵W，即

(7)

对于获得的特征矩阵W，采用连续的多个卷积层对其进行特征提取，每一层之间的卷积运算如图 2(b)所示，r+1层上的第k个卷积图的计算可以表示为[18]

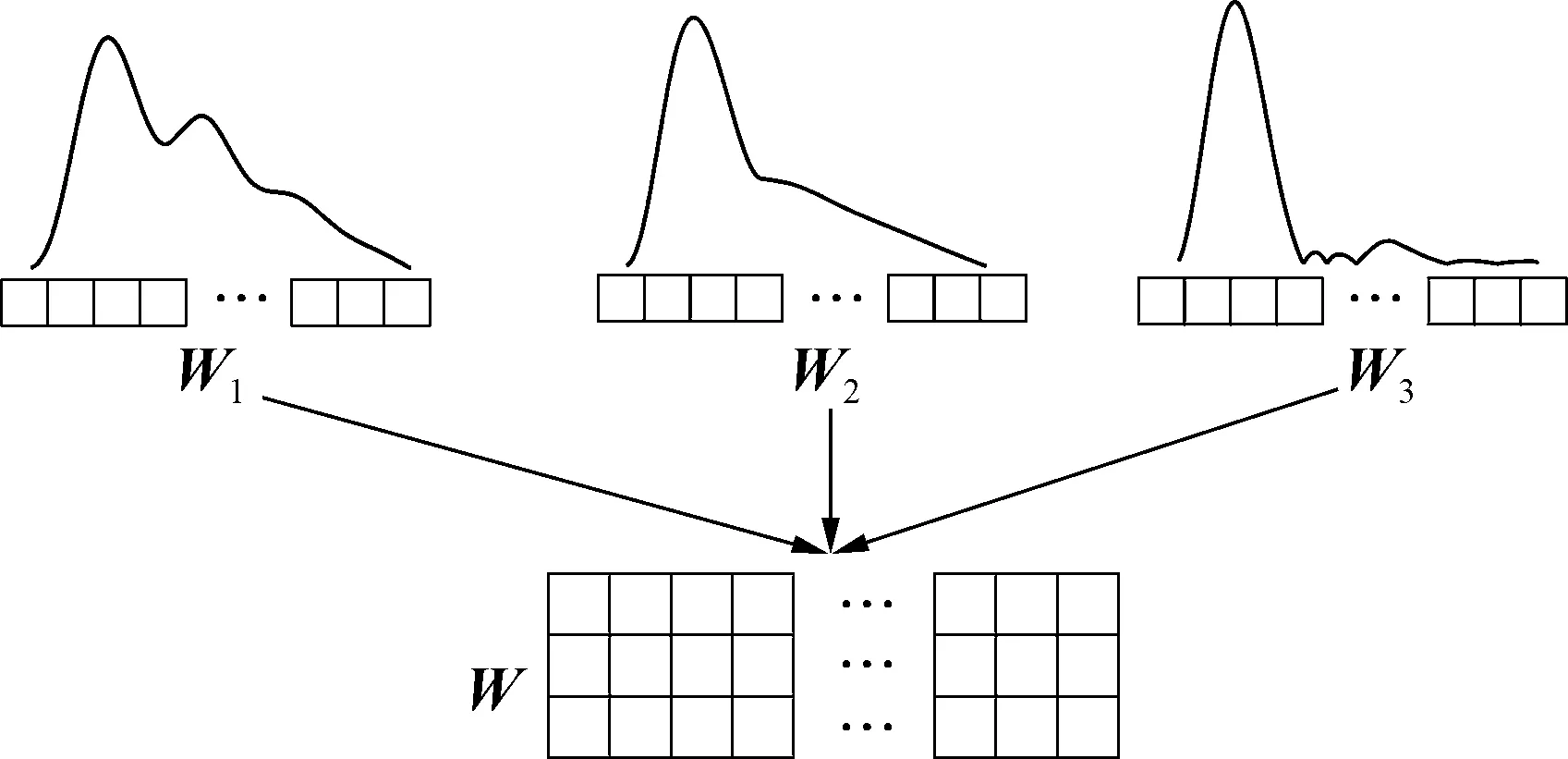
(a)生理波形特征矩阵

(8)

对于每一层卷积层(CONL)网络的输出，采用Relu激活函数来增强其非线性，如图2(c)所示，其函数表达式为

(9)

式中，X为Relu函数的输入值.在激活函数后需要对获得的特征图进行特征选择与特征过滤，以降低其维度，常见的操作包括池化运算和增大卷积步长.考虑波形矩阵在长度方向的尺度明显大于高度方向，故采用增大长度方向的卷积步长s1的方式来降低矩阵维度.

2.2 全连接神经网络

为综合考虑临床测量中的离散数值，采用图3所示的全连接神经网络(FCNN)来提取心率、脉搏波传输时间(TPWT)与待估计参数之间的依赖性.采用一种切线法来自动计算压力波形之间的TPWT值，如图3(a)所示，取波形最低点切线与上升支最大一阶导数点切线的交点为特征点，2个压力波形特征点之间的时间差则为TPWT值[19].

单个神经元对输入的作用如图3(b)所示，其中r+1层第g个神经元的输出Or+1,i可表示为

(10)

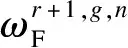
(a)特征点计算示意图

2.3 血流动力学参数反演DNN模型

如图4所示，建立了一个用于心血管血流动力学参数反演的混合多源输入深度神经网络(DNN)模型.图中，W为连续血压、血流波形，V为离散特征向量；CONL1(16×3×10)表示第1层卷积层，且其卷积核个数为16，高度和长度尺寸分别为3和10；FCL1(6×1)表示第1层全连接层，其神经元个数为6，其余卷积层和全连接层的参数可以此类推.卷积核在高度方向的步长为1，长度方向的步长为3.压平层用于将卷积得到的特征图重排列为一维向量，以便与全连接网络连接.融合层用于将2部分输入经各自网络处理后得到的向量串联，用于提取它们对输出的共同依赖性.采用预测值与实际值的均方误差(MSE)作为损失函数，同时采用反向传播算法来进行网络权重的更新.

图4 DNN模型结构

采用正向运行心血管物理模型的方式来获取可用样本.用于采样的参数如表1所示.其中Cβ_arm、Cβ_aor、Cβ_car和CR为待估计参数，均为无量纲值.RH为已知的测量值，在生理范围内改变RH和SV值以模拟不同的入口流量.

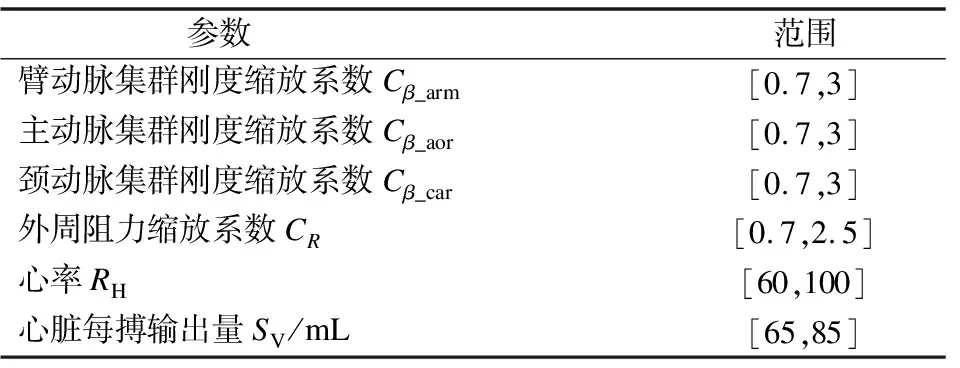
表1 参数抽样范围

在这些参数构成的参数空间内，采用Sobol法进行参数抽样，并将得到的参数样本输入心血管物理模型中进行正向计算，一个参数样本与其对应的模型输出波形便构成一个有效样本.共生成10 000个样本用于DNN模型训练，其中1 000个用于验证.额外生成200个样本用于网络的测试与评价.

2.4 集成网络模型

考虑到实际测量的波形常会受到噪声的干扰，采用一种集成网络模型来减小噪声对预测的影响.对于同一个DNN模型，重复对其进行基于随机初始化和随机批样本的网络训练，可得到一批权重参数收敛到不同值的DNN模型.在测试阶段，同时采用这些DNN模型进行预测，并将各模型的输出进行简单平均，其所得结果即为集成网络模型的输出.该模型可表示为

(11)

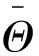
3 参数灵敏度分析及反演结果

3.1 参数灵敏度分析

图5给出了3处待测量部位的生理输出对不同参数的灵敏度.分别观察了Cβ_arm扰动对W1的影响、Cβ_car扰动对W3的影响、Cβ_aor和CR的扰动对W1和W2的影响，参数扰动统一设置为从1减小到0.7和从1增加到2.

如图5所示，Cβ_arm对肱动脉压力波形的主峰影响不大，对次峰影响明显，而Cβ_aor对2个压力波形的主峰和次峰都有着明显的影响.Cβ_car对颈动脉流速波形的震荡范围有较大影响，当Cβ_car增大时，波峰和波谷都有明显的减弱.CR与压力呈现正相关，能够使压力波形整体沿着垂直轴发生移动，且变化较为显著.由此可发现，Cβ_arm对于W1的影响相对较弱，而其余3个参数对于相应波形的影响都较为明显.

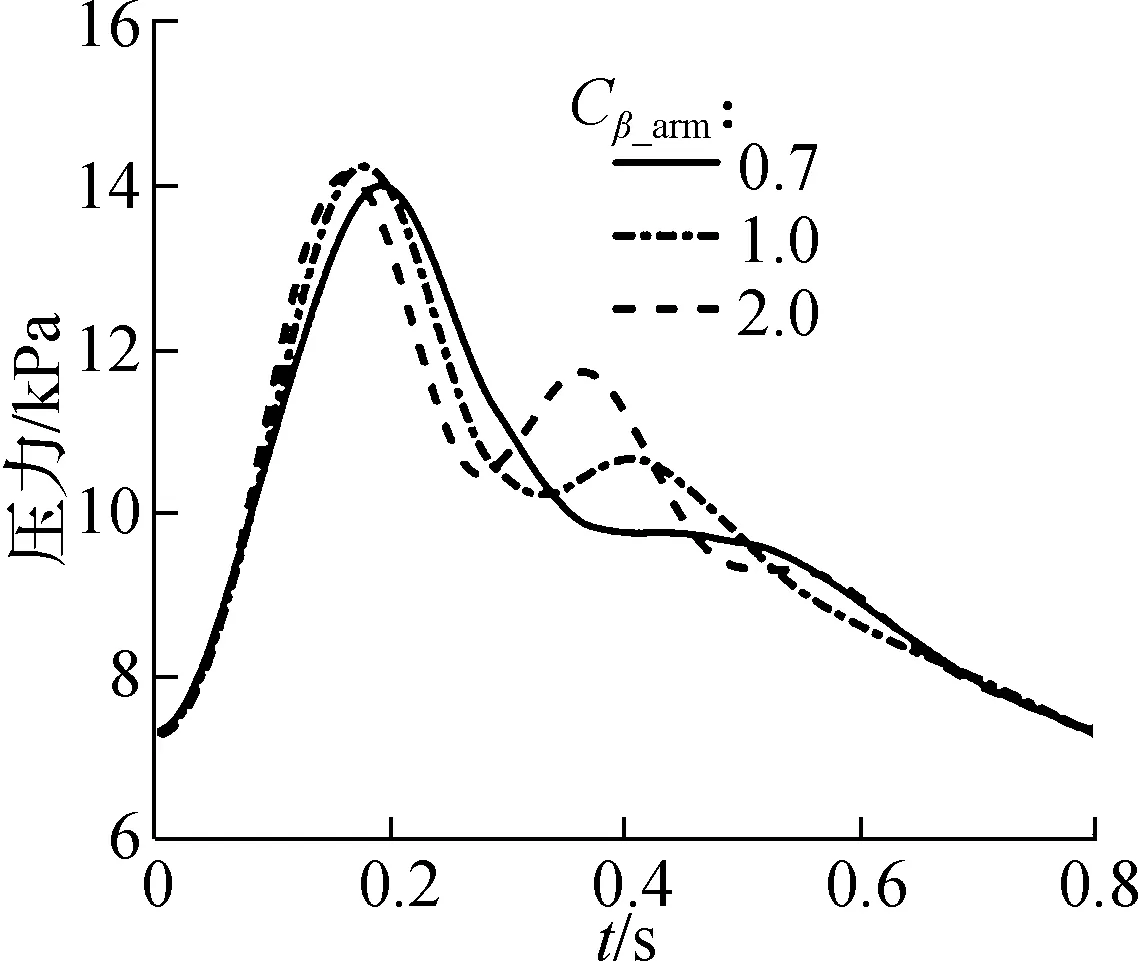
(a)不同Cβ_arm值下的W1

3.2 参数反演结果

在生理波形中添加白噪声N(0,σ2)来模拟实际测量的误差, 标准差σ依次从0增加到1.5.图6给出了单个DNN模型和集成网络模型在不同噪声干扰下的各参数反演情况，纵坐标为200个测试样本的参数真实值与反演值的MSE值.由图6(a)可见，当噪声标准差σ增加不超过0.5时，参数反演的精度变化相对平稳，且各参数MSE值相差不大.当σ进一步增加时，参数MSE值有明显上升，且Cβ_arm的MSE值上升的幅值明显高于其他3个参数.当σ增加到1.5时，各参数的MSE值达到最大，其中Cβ_arm的MSE值为0.028，远高于其他3个参数，其次是Cβ_car的MSE值，为0.008，Cβ_aor和CR的MSE值相对较小，分别为0.004和0.006.

可发现，在测量噪声增加时，参数Cβ_arm的反演精度会有显著下降.结合3.1节灵敏度分析不难发现，Cβ_arm对压力波形的影响较小，在噪声的干扰下，波形次峰的特征可能会有所减弱，导致DNN网络对其识别能力有所降低.

图6(b)给出了集成网络模型的反演结果.可以发现，各参数的变化趋势与单个DNN网络的结果基本相符，但在噪声幅值较大时，集成模型预测结果的MSE值明显低于单个DNN网络结果.其中，当σ=1.5时，Cβ_arm的MSE值减小为0.015，Cβ_aor、Cβ_car以及CR的MSE值也分别减小为0.003、0.005和0.003.

(a)单个DNN模型

进一步地，选取一组特定参数设置来分析所提DNN法的反演效果，其中，Cβ_arm、Cβ_aor、Cβ_car和CR的真实值分别为2.18、1.84、1.67和1.14，而RH和SV分别为70.87和72.65 mL.图7给出了噪声方差σ为1.5时集成网络模型中各DNN模型反演值的箱线图，图中线框值从上到下分别代表最大值、上四分位数、中位数、下四分位数、最小值，星号标记代表剔除的异常值.从图7可看出，正常值的分布较为集中，中位数的位置相对合理，且异常值数量较少，说明各DNN网络模型的预测性能基本一致，受波形噪声的影响，估计值在真实值附近波动.

图7 各DNN模型预测值箱线图

为进一步评估所提方法的参数估计效果，将DNN法与现有卡尔曼滤波(KF)法所得估计值进行对比，分别给出了各参数在不同噪声下的误差，如表2所示.可看出，噪声水平对于2个方法的估计误差有较大的影响，噪声增大时，估计误差总体呈现上升趋势；DNN法的估计误差明显低于KF法，两者的误差对比在较低噪声水平下并不显著，但随着噪声的提高，DNN法的估计精度具有显著的优势.

表2 DNN法与KF法反演误差的对比 %

对于血流动力学参数反演，个性化后的模型输出与实际测量波形的误差是评估参数反演是否有效的重要标准.因此，在噪声方差σ为1.5的条件下，分析了模型输出波形与实际测量波形的误差，图8给出了这组参数的模型仿真波形与测量波形的对比.可以发现，2种方法个性化后的仿真波形与测量波形基本一致.计算可得，DNN法模型的模拟输出与测量波形均方根误差(RMSE)分别为242 Pa、233 Pa和2.21 cm/s，而对应的KF法波形RMSE为665 Pa、595 Pa和3.23 cm/s.可看出，所提DNN法可以更好地拟合实际测量结果.

(a)波形W1

4 讨论

基于深度学习技术，提出了一种新的血流动力学参数反演方法，并通过数值模拟对其进行了初步验证.结果表明，相比于现有技术，本方法同时提高了参数反演的效率与精度，能够实现持续的动态监测，具有较高的实际意义.现阶段的研究存在以下不足：① 参数的可识别性包括灵敏度分析和相关性分析，考虑到相关性分析在文献[10]中已经给出，故本文未对此部分展开叙述；② 利用临床中较为常见的3处波形对包括刚度与阻力在内的4个参数进行反演，缺少局部血管的参数反演测试.临床应用时可根据反演任务的不同建立多个网络模型，以满足周身及局部个体化建模的需要；③ 考虑到血管长度、直径等参数也会对血流速度与压力产生影响，在应用所提方法时，需要对已经训练好的模型进行少量的迁移学习，未来工作中将进一步研究迁移算法对反演精度的影响.

5 结论

1)基于深度学习技术提出了一种新的心血管血流动力学参数反演方法，并提出了一种集成网络模型来降低测量噪声对参数反演的影响.

2)对所提方法进行数值模拟验证，结果表明，所提方法可以准确地从带有噪声的测量中反演出目标参数，且反演过程无需人工操作和模型正向计算，兼顾了反演效率与反演精度.

3)未来工作将对所提方法进行基于迁移学习算法的优化与扩展，使该方法能够有效应用于不同个体.