纳米偏高岭土水泥浆颗粒水膜厚度与流变参数相关性

李秋超 范颖芳 李学良

(大连海事大学土木工程系, 大连 116026)

纳米偏高岭土赋予水泥基材料优异的力学性能和耐久性[1-2],但其颗粒粒径小,具有较高的比表面积和表面能,在水泥浆中容易发生团聚并包裹拌和水,引起浆体中起润滑作用的自由水量降低,流动性变差,影响浆体拌制、浇筑及硬化后性能.新拌水泥浆中拌和水首先填充颗粒间空隙,然后剩余水包裹颗粒表面形成水膜,水膜厚度易于利用多余水率和颗粒比表面积得到.流变参数(屈服应力、塑性黏度、滞回面积等)可全面、定量评价水泥浆流变性,然而流变设备价格昂贵,多限于实验室使用,在实际工程中流变参数获取受到限制.水膜在浆体流动时起润滑作用,水膜厚度、流变参数均与浆体用水量有关,若通过水膜厚度合理预测流变参数,可为实际工程中水泥浆流变性评价提供一种快速、便捷、可靠的方法.

水泥浆颗粒水膜厚度一经提出便受到广泛关注,国内外学者相继建立水膜厚度与流变参数的关系,取得了一定的研究成果[3-6].Ye等[3]研究发现,水泥浆水膜厚度与流动度、流动速率存在反比例关系;Vance等[4]认为水膜厚度与水泥浆屈服应力、塑性黏度存在线性关系;Kwan等[5]研究表明水膜厚度与水泥浆流动速率、扩展度存在指数关系;肖佳等[6]认为水膜厚度与屈服应力存在反比例关系.可以看出,上述研究中有关水膜厚度与流变参数之间究竟存在何种关系尚存在较多争议,相关研究有待进一步开展.迄今为止,在NMK水泥基材料流变性研究方面,主要围绕NMK掺量对流变性能(混凝土坍落度值[7]、流动度[8]、水泥浆触变性[9]、屈服应力和塑性黏度[10])的影响展开,得到了一些有益的结论.然而,有关NMK水泥浆颗粒水膜厚度及其与流变参数的相关性研究尚未见报道.

为了厘清NMK水泥浆颗粒水膜厚度与流变参数的关系,本文首先测得NMK水泥浆颗粒堆积密度,获得浆体多余水量,结合颗粒比表面积得到水膜厚度;然后采用流变仪测得NMK水泥浆屈服应力、塑性黏度等流变参数;通过泌水性试验分析NMK掺量对水泥浆泌水性的影响,并结合多余水率、颗粒沉降理论揭示水泥浆泌水机理.基于试验结果,提出基于水膜厚度的流变参数预测模型,并利用相关文献试验资料验证了该预测模型的适用性和有效性.

1 试验

1.1 试验材料

试验水泥选用小野田P·O 42.5R普通硅酸盐水泥;试验用水为自来水;纳米偏高岭土为内蒙古超牌偏高岭土有限公司生产,由高岭石原矿煅烧后研磨而成.水泥和纳米偏高岭土化学成分见表1.纳米偏高岭土和水泥中位粒径(D50)分别为1.75和14.26 μm,比表面积分别为4.09和0.58 m2/g.纳米偏高岭土XRD图谱、粒径分布、TEM形貌及颗粒片层厚度概率统计如图1所示.可以看出,NMK衍射峰呈弥散状,呈现为结晶态较差的过渡相;由纳米偏高岭土TEM形貌及颗粒片层厚度概率统计分析发现NMK片层厚度远小于100 nm,可视为纳米材料(在三维空间中至少有一维处于纳米尺度).减水剂采用上海臣启化工有限公司生产的CQJ-JSS02型聚羧酸系高效减水剂粉末,减水率为25%.

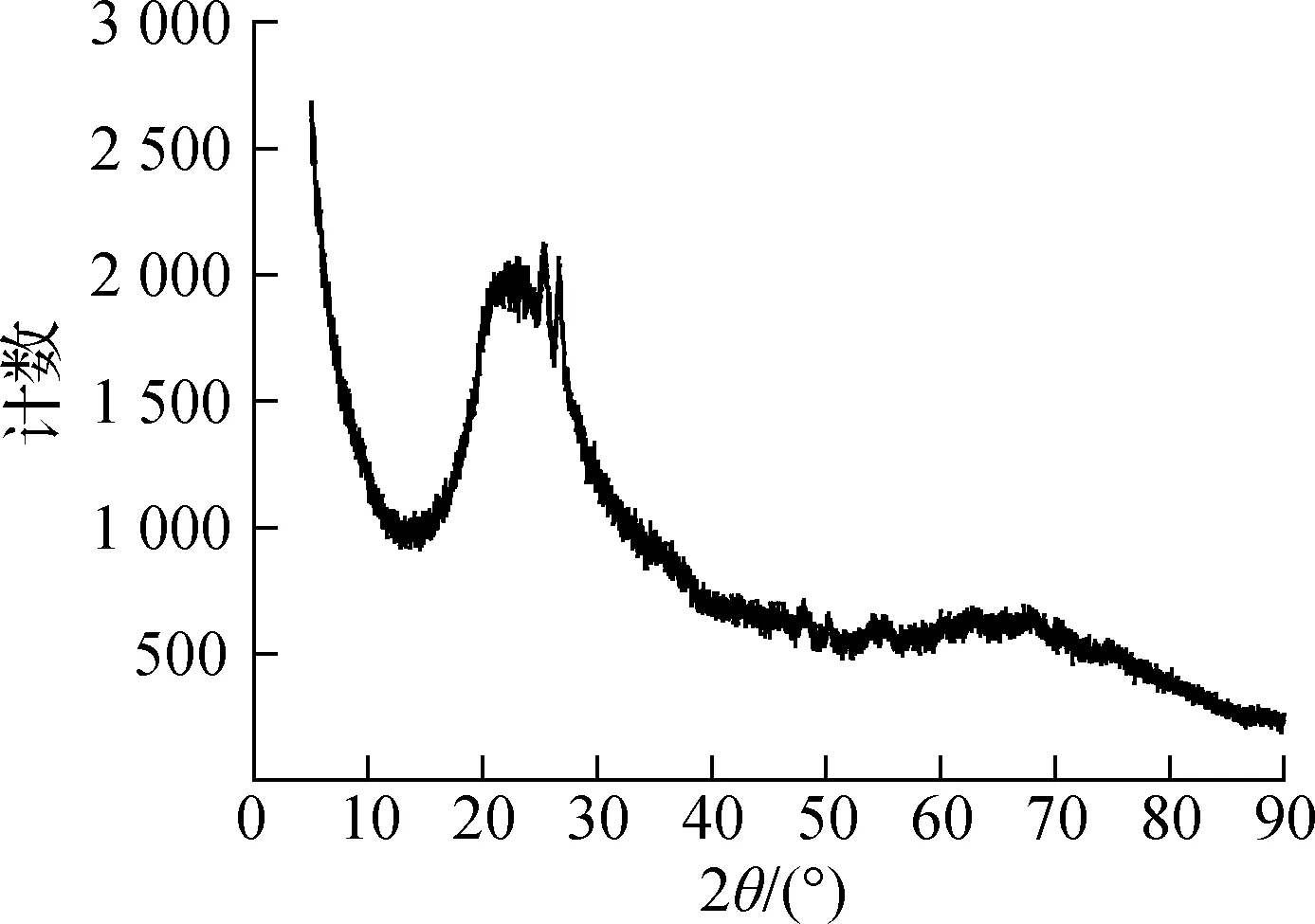
(a)XRD图谱

表1 水泥和纳米偏高岭土化学成分 %

1.2 试件制作

NMK水泥浆流动性和流变性试验考虑3种水胶质量比w/b(0.40、0.45、0.50),减水剂用量依次为3种水胶比水泥浆中胶凝材料总质量的0.16%、0.14%和0.12%[10].考虑4种掺量(分别为胶凝材料总质量的1%、3%、5%、10%)NMK等质量替代水泥,不同掺量NMK水泥浆试样分别记为NP1、NP3、NP5和NP10;未掺NMK水泥浆记为NP0.纳米偏高岭土颗粒粒径小,比表面积大,在水泥浆中容易发生团聚,为提高纳米偏高岭土在水泥浆中的分散性,在浆体制备时首先将NMK在水中超声分散15 min[10],然后将混合溶液加入水泥进行拌制;浆体制备依据《公路工程水泥及水泥混凝土试验规程》(JTG E30—2005)进行.泌水性试验水胶质量比为0.50,减水剂用量为胶凝材料总质量的0.12%.标准稠度用水量试验、泌水性试验浆体制备均与上述方法相同.

1.3 试验方法及过程

流变性试验采用Anton Paar MCR 301流变仪,选用CC27测试系统.流变测试于水泥与水接触10 min时进行,环境温度为20 ℃.测试过程分为预剪切阶段和数据采集阶段,流变测试程序与文献[10]一致.水泥浆流动度试验依据《混凝土外加剂匀质性试验方法》(GB/T 8077—2012);胶凝颗粒堆积密度测试分别采用标准稠度用水量法[11]和最大颗粒浓度法[12].泌水率试验依据文献[13]测试方法进行,当水泥与水接触开始计时,浆体制备完成后即刻转移至相应封闭容器中,记录浆体的初始高度h0(本试验中均为100 mm),至规定水化时间时测量浆体上部泌水高度记为ht,不同水化时间NMK水泥浆泌水率计算公式为αt=(ht-h0)/h0×100%.

1.4 NMK水泥浆颗粒堆积密度计算

胶凝材料堆积密度测试方法众多,如干堆积密度法、湿堆积密度法等.其中,干堆积密度法取决于颗粒压实状态,且当颗粒尺寸小于100 μm时,在范德华力、静电吸附作用下,颗粒发生团聚,干堆积方法不再适用[12,14].因此,本文选用目前广泛采用的2种湿堆积密度方法(标准稠度用水量法[11]和最大颗粒浓度法[12])测试NMK水泥浆颗粒堆积密度,通过对比确定一种简单、准确的方法.

1.4.1 标准稠度用水量法

Lecomte等[11]认为,当水泥拌和物用水量达到标准稠度用水量时,浆体中拌和水恰好填充固体颗粒间空隙.胶凝体系颗粒堆积密度可用下式计算：

(1)

式中,φ为颗粒堆积密度;ws为标准稠度用水的质量;b为水泥和纳米偏高岭土颗粒的总质量;ρb为水泥和纳米偏高岭土混合粉体的密度,ρb=ρNMKRNMK+ρPCRPC,其中,ρPC和ρNMK分别为水泥和纳米偏高岭土的密度,RPC和RNMK分别为水泥和纳米偏高岭土颗粒体积与混合粉体颗粒体积的比值,二者和为1.

1.4.2 最大颗粒浓度法

Wong等[12]认为水泥浆用水量达到标准稠度用水量时未必恰好填充颗粒间空隙,并提出采用最大颗粒浓度法计算胶凝颗粒堆积密度.当水固比较大时,固体颗粒分散于水中,颗粒浓度随水固比增大而减小;当水固比较小时,不足以与颗粒形成浆体,颗粒浓度随水固比降低而减小.因此,存在临界水固比使颗粒浓度最大.最大颗粒浓度法的计算公式为

(2)

式中,Vc为容器体积;Vs纳米偏高岭土和水泥颗粒混合粉体的体积[11],即

(3)

其中,ρw为水的密度;Rw为水的体积与混合粉体颗粒体积之比;M为容器中浆体的质量.

1.5 水膜厚度计算

在胶凝颗粒体系中,未加水时胶凝颗粒紧密堆积;加入一定量的水时,拌和水逐渐填充颗粒间空隙,如图2(a)所示,此时颗粒不发生流动.当拌和水完全用于填充颗粒间空隙时,颗粒水膜厚度恰好为0,如图2(b)所示.当浆体中拌和水量高于颗粒间空隙的需水量时,填充完颗粒空隙的多余水(自由水)包裹颗粒表面形成水膜,如图2(c)所示;浆体中自由水量越多,颗粒水膜厚度越大[13].

(a)紧密堆积

新拌水泥浆颗粒水膜厚度定义为浆体中多余水率与颗粒比表面积(平均比表面积)的比值[13],即

(4)

式中,WT为颗粒水膜厚度,μm;u′为多余水率,u′=uw-uv,其中,uw为水的体积与固体颗粒体积之比,uv为空隙体积与固体颗粒体积之比,uv=(1-φ)/φ;AT为水泥浆体中颗粒总比表面积,AT=ANMKRNMK+APCRPC,其中,ANMK、APC分别为纳米偏高岭土颗粒和水泥颗粒的比表面积.

2 试验结果分析与讨论

2.1 NMK水泥浆颗粒堆积密度

采用标准稠度用水量法和最大颗粒浓度法测得NMK水泥浆颗粒堆积密度,结果如表2所示.可看出,2种方法测试结果一致,NMK水泥浆颗粒堆积密度差值不超过2%.考虑到最大颗粒浓度法无需进行水泥浆标准稠度试验，且堆积密度更易获取,本文采用最大颗粒浓度法所得颗粒堆积密度进行后续水膜厚度计算.

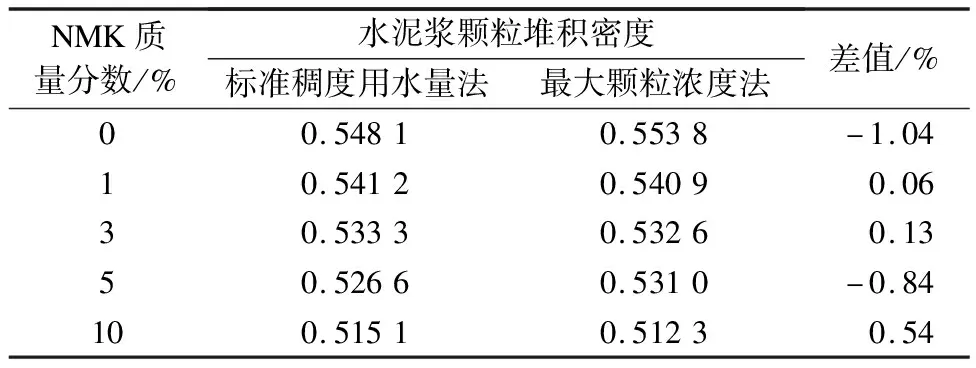
表2 不同方法所得NMK水泥浆颗粒堆积密度

堆积密度、标准稠度用水量与NMK掺量关系如图3所示.可以看出,NMK导致水泥浆颗粒堆积密度减小,需水量增大;掺减水剂水泥浆颗粒堆积密度降低.究其原因,纳米材料颗粒粒径小,具有较高的比表面积和表面能,颗粒间范德华力、静电力产生的黏附作用引起颗粒团聚,造成颗粒间空隙量增加,堆积密度减小[12].此外,浆体中需要更多拌和水填充颗粒间空隙,需水量增加.在水泥浆中掺入减水剂后,减水剂分子吸附于水泥或NMK颗粒表面,使颗粒表面带有同种电荷(负电荷),颗粒间产生静电斥力,絮凝结构解体,胶凝颗粒得到有效分散[10,15],固体颗粒堆积更加紧密,颗粒堆积密度较未掺减水剂时显著增加.

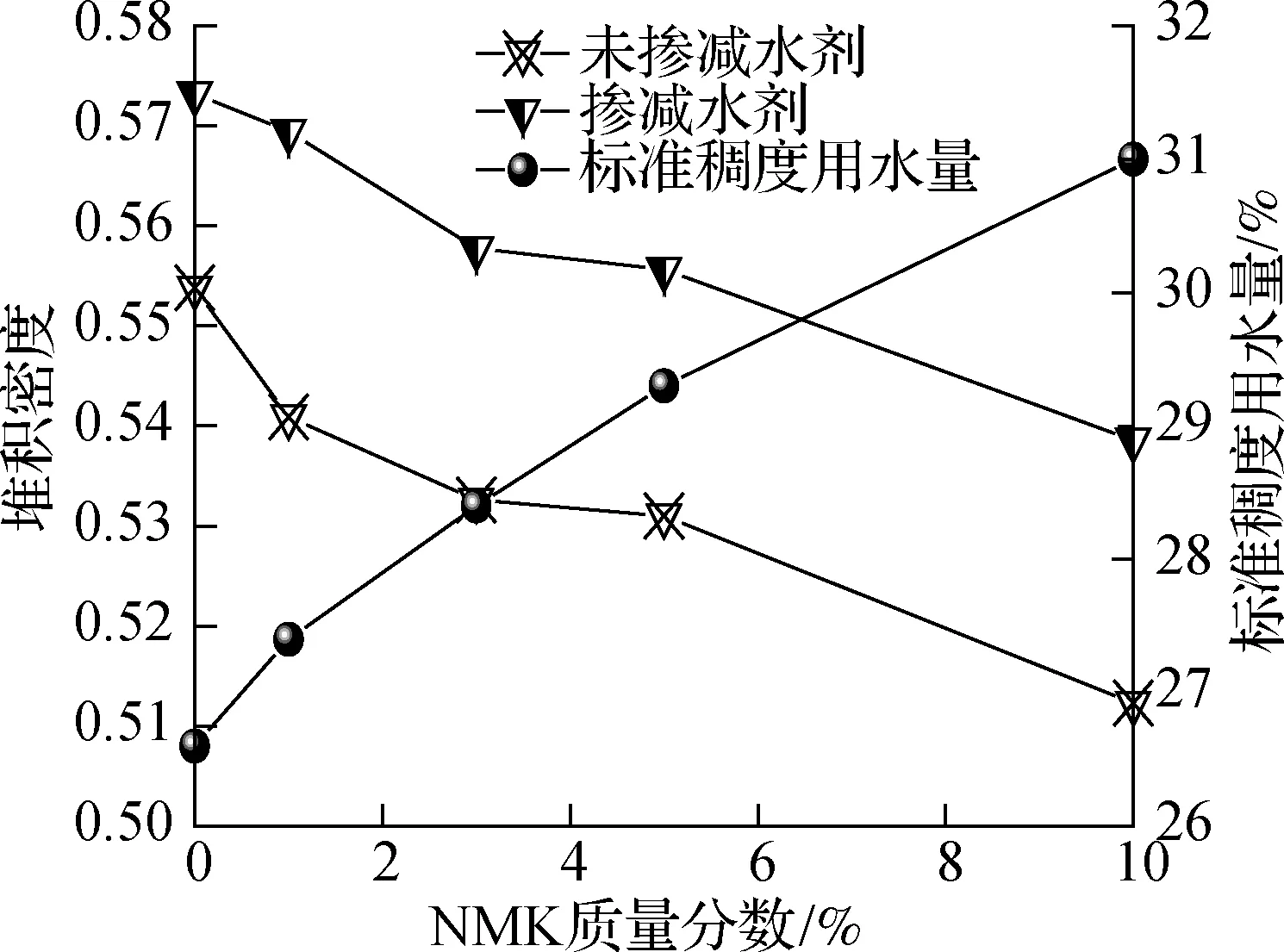
图3 堆积密度、用水量与NMK掺量的关系

2.2 NMK水泥浆颗粒水膜厚度

不同水胶比水泥浆颗粒水膜厚度与NMK掺量的关系如图4所示.可以看出,NMK导致水泥浆颗粒水膜厚度降低,二者之间存在幂函数关系.当NMK掺量一定时,水胶比越大,浆体中起润滑作用的自由水量越多,颗粒水膜厚度越大.

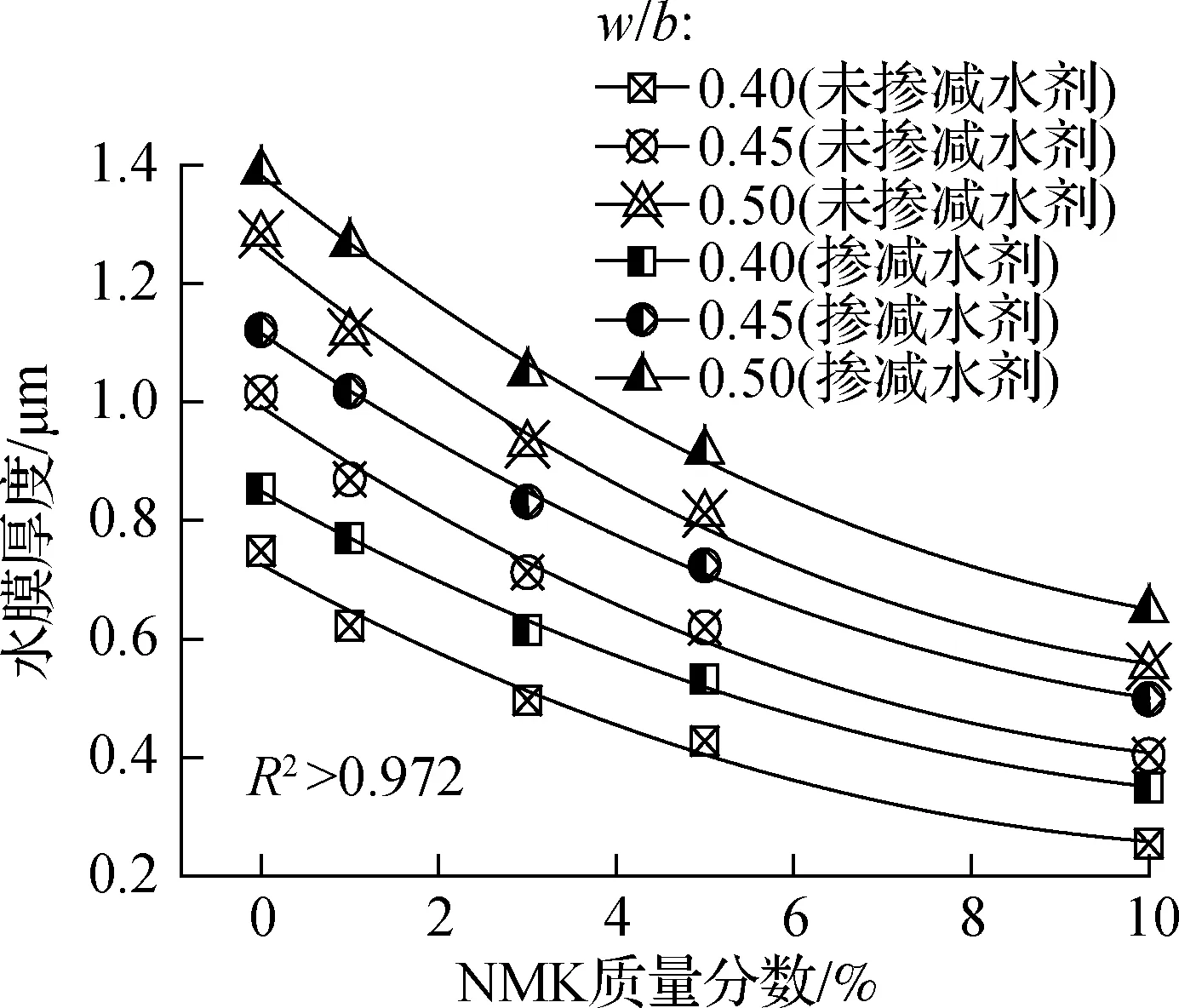
图4 水膜厚度与NMK掺量的关系

在水泥浆中掺入减水剂后,一方面浆体中颗粒堆积密度增大,颗粒间空隙率减小,用于填充颗粒间空隙的拌和水量减少,浆体中自由水量增多;另一方面,减水剂对絮凝结构有着分散作用,引起絮凝水的释放,自由水量进一步增加,从而引起颗粒水膜厚度增大.

2.3 NMK对水泥浆絮凝水释放率、泌水率的影响

2.3.1 絮凝水释放率

在新拌水泥浆体系中,拌和水的存在形式一般包括3种：填充固体颗粒间空隙的水、絮凝结构包裹的絮凝水、包裹颗粒表面形成水膜的自由水[16-17].当拌和水填充完颗粒间空隙后,絮凝水和自由水相互转化;由于减水剂对絮凝结构有着一定的分散作用,通过掺、未掺减水剂NMK水泥浆中多余水率的变化,可以确定减水剂对NMK水泥浆絮凝水释放率的影响;絮凝水释放率定义为掺减水剂水泥浆多余水率与未掺减水剂多余水率的差.不同掺量NMK水泥浆絮凝水释放率如表3所示.

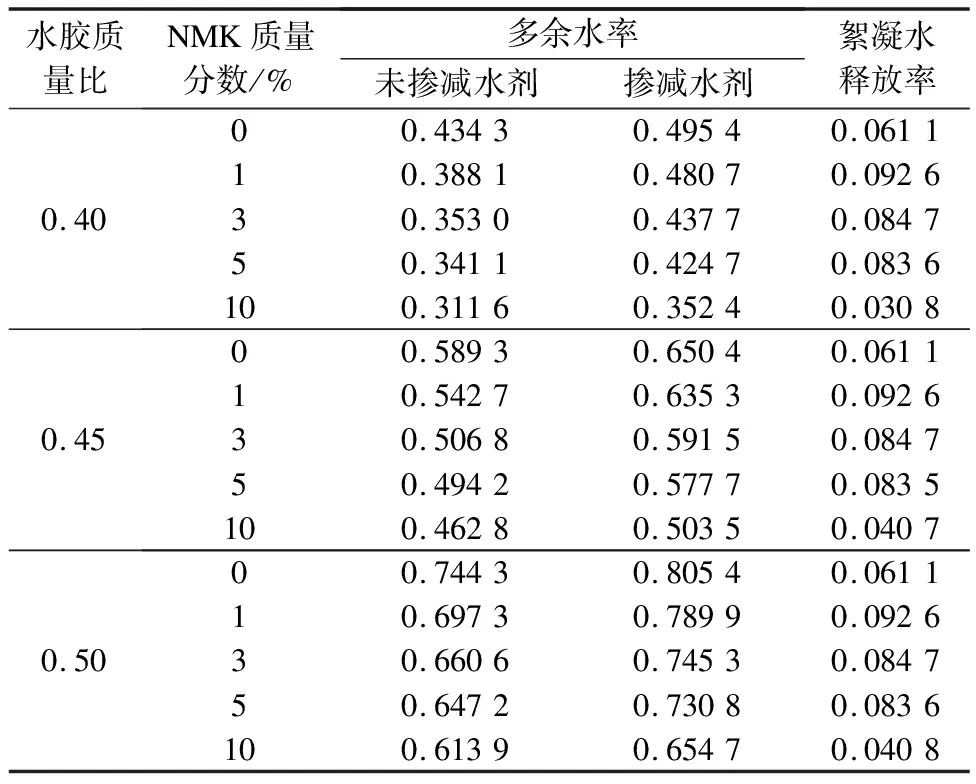
表3 掺减水剂NMK水泥浆絮凝水释放率

由表3可以看出,浆体中多余水率随NMK掺量的增加而减小,水胶质量比0.40掺质量分数10% NMK水泥浆多余水率较普通(未掺NMK)水泥浆降低28.25%;掺减水剂水泥浆多余水量增加,这与减水剂对絮凝结构的分散作用有关.另外,絮凝水释放率受NMK掺量影响较大,受水胶比影响小.当减水剂用量一定时,絮凝水释放率随NMK掺量先增大后减小;掺质量分数1% NMK水泥浆絮凝水释放率最大;当NMK掺量继续增大时,絮凝水释放率降低.究其原因,纳米偏高岭土是一种纳米黏土,黏土颗粒与水泥颗粒相比,其对减水剂有着更强的吸附作用[18].因此,当减水剂用量一定时,减水剂对絮凝结构的分散作用随NMK掺量增加而降低,絮凝水释放率随之减少.

为明确絮凝结构对NMK水泥浆中自由水的影响,制备水胶质量比1∶1的未掺减水剂水泥浆.为避免观测过程中水泥水化的影响,至水泥与水接触10 min时,加入酒精稀释50倍后采用光学显微镜观测其微观形貌(见图5)[10].可以看出,未掺NMK水泥浆中絮凝结构相对较少;随NMK掺量增加,絮凝结构逐渐增多,絮凝体包裹更多拌和水,故浆体中自由水量减少.此结论与表3中自由水率随NMK掺量的变化规律一致.

(a)NP0

2.3.2 泌水率

由上述分析可知,掺减水剂使水泥浆体中多余水量增加,而多余水对浆体流动起促进作用,但过量多余水必然引起浆体的泌水行为,进而影响其硬化后性能.通过泌水性试验测得不同静置时间NMK水泥浆泌水率,结果如图6所示.可以看出,水泥浆泌水率随静置时间延长而增大.NMK导致水泥浆泌水率显著降低,掺质量分数10%NMK水泥浆静置15、180 min后的泌水率仅为普通水泥浆泌水率的6.25%和16.90%,表明掺NMK水泥浆具有较好的保水性.

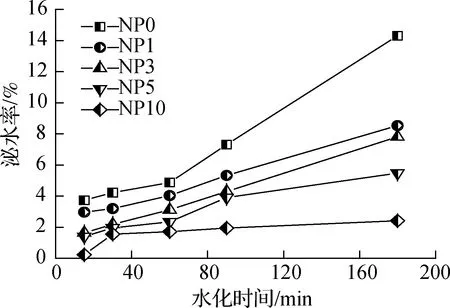
图6 水泥浆泌水率与NMK掺量的关系

由于水泥浆泌水性与浆体用水量及颗粒沉降有关,当水泥、NMK颗粒在水溶液中保持稳定时,颗粒沉降遵循Stokes定律[2],即

(5)

式中,VG为颗粒沉降速度,m/s;R为颗粒半径,m;μL为介质黏度,Pa·s;ρP为颗粒密度,g/cm3;ρL为介质密度,g/cm3;g为重力加速度,m/s2.

由式(5)可知,沉降速率与颗粒半径、密度成正比.由于NMK颗粒粒径、密度小,当NMK等质量替代水泥后,浆体中颗粒沉降速率降低,泌水率随之降低.另外,结合图5可知,NMK引起浆体中絮凝结构增加,絮凝体包裹拌和水,引起浆体中自由水量减少,泌水率降低.

2.4 NMK水泥浆流变参数

流变曲线下行段数据可重复性强,具有一致性[19],故选取流变曲线下行段数据进行分析.未掺减水剂NMK水泥浆(当水胶质量比为0.40、NMK质量分数为10%时,超出流变仪扭矩测试量程)流变特征符合修正Bingham模型,即

(6)

掺减水剂普通水泥浆为非屈服应力流体,而掺减水剂NMK水泥浆流变特征符合Herschel-Bulkley模型,即

(7)

式中,K为稠度系数(常数),Pa·sn;n为材料的流动指数,当n<1时,混合物为剪切稀化,当n>1时,混合物为剪切增稠;且n与1差值越大,其剪切增稠或剪切稀化行为越显著.NMK水泥浆流变参数如表4所示.

表4 NMK水泥浆流变参数

2.5 未掺减水剂时水膜厚度与流变参数的关系

2.5.1 水膜厚度与流动度

水泥浆流动度、颗粒水膜厚度均与浆体中多余水量有关.通过归纳法建立NMK水泥浆颗粒水膜厚度与流动度的关系(见图7).

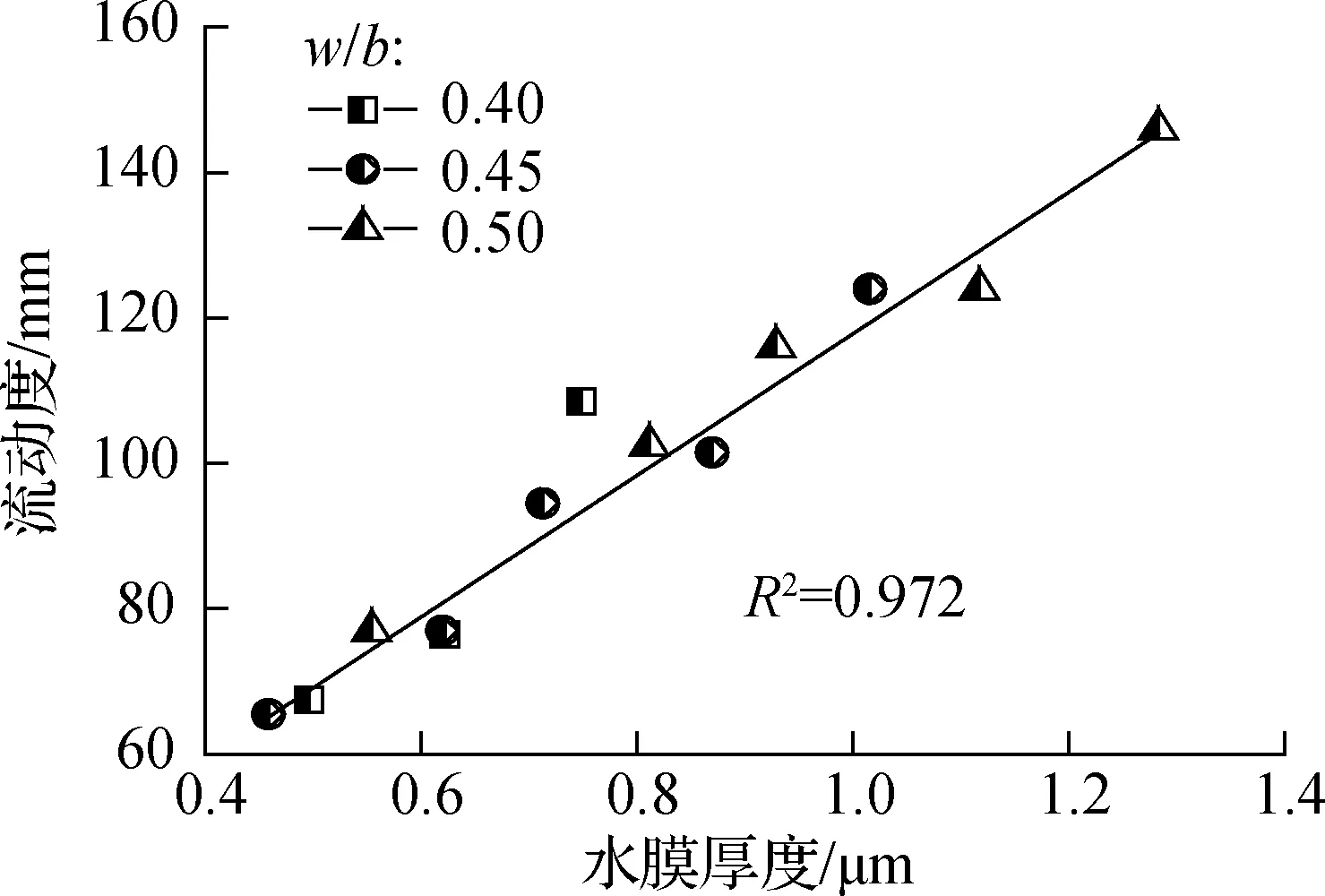
图7 NMK水泥浆水膜厚度与流动度的关系

新拌NMK水泥浆流动度随颗粒水膜厚度增加线性增大,二者关系可表示为

D=a+kWT

(8)

式中,D为流动度,mm;a、k为常数.新拌水泥浆开始流动时,水膜对颗粒起润滑作用;随水膜厚度增加,固体颗粒或絮凝体间摩阻力减小,水泥浆流动度增大.

2.5.2 水膜厚度与屈服应力

屈服应力是浆体开始流动时需要克服的最大应力.Ye等[3]研究表明,水泥浆颗粒水膜厚度越小,屈服应力越大.NMK水泥浆屈服应力与水膜厚度关系如图8所示.可以看出,NMK水泥浆颗粒水膜厚度低于0.6 μm时,屈服应力降低速率高于水膜厚度增长速率.NMK水泥浆屈服应力随水膜厚度增大而减小,二者关系可表示为

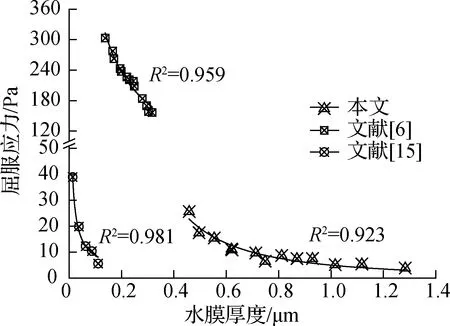
图8 NMK水泥浆水膜厚度与屈服应力的关系

τ0=kWTm

(9)

式中,m为常数.采用该模型对肖佳等[6]、Kwan等[15]试验数据进行预测,所得屈服应力预测值与试验值吻合较好.因此,通过该数学模型基于水膜厚度预测NMK水泥浆屈服应力是一种可靠的方法.

2.5.3 水膜厚度与塑性黏度

塑性黏度是水泥浆内部固体颗粒内摩擦性质的量度,反映浆体变形速度大小.NMK水泥浆塑性黏度与水膜厚度的关系如图9所示.可以看出,NMK水泥浆塑性黏度随水膜厚度增大而减小.究其原因,一方面纳米偏高岭土具有较高的表面能,在浆体中容易形成絮凝结构,包裹拌和水,导致浆体中自由水量降低;另一方面,纳米偏高岭土比表面积大,胶凝体系颗粒总比表面积随NMK掺量增加而增大.由式(4)可知水膜厚度与比表面积成反比,与浆体中自由水量成正比,故掺NMK水泥浆颗粒水膜厚度降低,颗粒间摩阻力增加,塑性黏度增大.水膜厚度与塑性黏度存在幂函数关系,可表示为

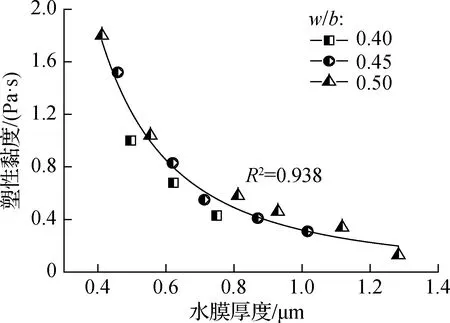
图9 NMK水泥浆水膜厚度与塑性黏度的关系

μ=kWTm

(10)

在新拌水泥浆中,固体颗粒之间距离小(一般认为颗粒间距离为水膜厚度的2倍),颗粒间存在引力(即黏聚力),该引力是水泥浆产生黏性的主要支撑[20].目前,颗粒间引力与黏度的关系未得到定量评价.本文基于Flatt等[13,21]提出的新拌水泥浆中颗粒间引力公式获得NMK水泥浆颗粒间引力,即

(11)

式中,Fa为水泥浆体中颗粒间引力;A(h)为Hamaker常数,与材料介电性能有关,在水泥相材料中约为0.44×10-20J;h为固体颗粒间距离,其大小为水膜厚度的2倍.

获得NMK水泥浆颗粒间引力后,建立颗粒间引力与塑性黏度的关系,如图10所示.可以看出,NMK水泥浆塑性黏度与颗粒间引力存在线性关系,塑性黏度随颗粒间引力增加而增大,通过颗粒间引力同样可以较好地预测NMK水泥浆塑性黏度.

图10 颗粒间引力与塑性黏度的关系

2.5.4 水膜厚度与触变性

剪切应力-剪切速率上、下行曲线形成滞回环.新拌水泥浆滞回环面积即触变性大小取决于浆体内部絮凝结构数量[22].絮凝结构是由新拌水泥浆内部颗粒在范德华力、静电引力作用下形成[17],由式(8)可知,颗粒间引力与水膜厚度存在负相关性,故水膜厚度大小在一定程度上影响絮凝结构生成.NMK水泥浆滞回面积与水膜厚度的关系如图11所示,其可表示为

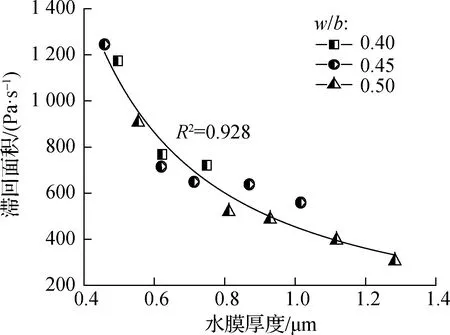
图11 NMK水泥浆水膜厚度与滞回面积的关系

Athix=kWTm

(12)

式中,Athix为滞回面积,Pa/s.颗粒水膜厚度越大,水泥浆触变性越小.

2.6 减水剂影响下水膜厚度与流变参数的关系

掺减水剂NMK水泥浆颗粒水膜厚度与流变参数的关系如图12所示.由图12(a)可以看出,掺减水剂水泥浆颗粒水膜厚度与流动度存在线性关系.由图12(b)可看出,屈服应力与水膜厚度之间存在非线性关系,屈服应力随水膜厚度增大而减小.掺减水剂NMK水泥浆塑性黏度通过传统流变模型无法获得,其与水膜厚度的关系有待进一步研究.由图12(c)可看出,NMK水泥浆滞回面积随水膜厚度增大呈减小趋势;且当水膜厚度增大时,滞回面积的减小速率与NMK掺量有关：当NMK质量分数大于1%时,滞回面积随水膜厚度的减小速率较小.掺减水剂NMK水泥浆水膜厚度与流变参数的关系受NMK掺量、水胶比、减水剂等多因素影响,相关研究有待深入探讨.

(a)流动度与水膜厚度

3 结论

1)标准稠度用水量法和最大颗粒浓度法测得NMK水泥浆颗粒堆积密度结果一致,2种方法测量差值不超过2%.NMK导致水泥浆颗粒堆积密度、水膜厚度减小,掺质量分数10% NMK水泥浆颗粒堆积密度、水膜厚度(水胶质量比0.40)较普通水泥浆分别降低7.5%、65%.

2)减水剂导致NMK水泥浆颗粒堆积密度和水膜厚度增大,掺质量分数10% NMK水泥浆(水胶质量比0.40)颗粒水膜厚度较未掺减水剂时增加37%.NMK引起水泥浆泌水率显著降低,掺质量分数10% NMK水泥浆泌水率(静置15 min)较普通水泥浆降低约93%.

3)基于水膜厚度建立的水泥浆流变参数(流动度、屈服应力、触变性等)预测模型所预测的流变参数与试验值吻合良好.通过已有文献中试验资料对屈服应力预测模型进行了验证,表明该模型预测精度高,适用范围广.