基于Spark的K-means快速聚类算法的优化

王全民，胡德程

(北京工业大学信息学部，北京100022)

1 引言

K-means[1]算法(K-means algorithm)是一种无监督聚类算法，主要是解决无标签数据聚类问题。如信息检索、文本挖掘等各个领域都有广泛应用。随着信息时代的到来，各领域的数据在速度、体积以及多样性都急剧上升，普通的数据规模达到了TB级甚至PB级。在海量数据背景下，对K-means算法性能要求也越来越高，故传统K-means算法越来越难适应海量数据。针对标准K-means算法依赖初始K个质心点，若选择的初始中心点不恰当以及更新中心点的冗余计算，往往会得到不理想的全局最优中心点和执行效率。

如何优化初始聚类中心点[2]的选择，提升K均值法的收敛速度和准确率是本文的主要研究方向。文献[3]通过将粒子群优化PSO与K均值法结合，采用PSO来得到初始聚类质心，以此提高K均值法的全局搜索能力。文献[4]利用近邻图来完成K-means算法的初始中心点的选择，避免随机选择初始点而带来的局部最优解问题。文献[5]利用hash抽样函数和MapReduce[6]计算框架来处理数据聚类，提高K均值算法的执行效率。本文使用最大距离算法优化初始中心点的选取，采用形态学相似距离提高准确率，网格空间减少冗余计算。

本文在Spark[7]并行计算框架下对K-means算法进行优化和实现，提高对海量数据的处理能力。采用的数据集是UCI网站上的glass，abalone，Aggregation，实现SMGK-means算法来验证其准确性，有效性以及加速性。

2 相关研究

2.1 Spark计算框架

本文选择Spark实现SMGK-means算法而非MapReduce即MR[8]，主要是Spark扩展了MR计算模型，具有MR的优点；与MR相比SparkJob[9]计算的中间结果RDD[10]可保存在节点内存中，无需从HDFS或者磁盘上读取数据，故Spark能很好地适用于迭代式的MR算法。Spark的系统架构如图1所示。

图1 Spark并行框架结构

Spark处理数据比MR快的原因如下。首先，Spark是基于内存迭代式计算；其次，Spark的数据结构是分布式数据集RDD[10](Resilient Distributed Dataset)，RDD将数据存储在节点executor内存中，通过划分分区优化数据分布。最后，Spark的DAG计算模型和惰性求值。Spark的算子操作分为两种即Transformation和Action，调用Transformation操作时如Map，flatMap，并不会立即执行，而在内部记录操作，形成DAG计算模型，当遇到Action操作时，会立即执行相应的Transformation操作。Spark Job的逻辑执行如图2所示。

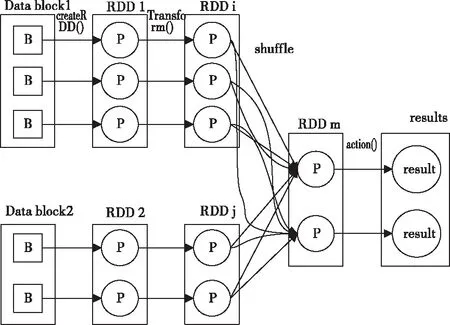
图2 Spark Job的逻辑执行图

2.2 K-means算法

传统K均值法是无监督聚类算法，输入样本中只有特征而没有标签，从待聚类的原始Dataset中随机选取K个数据点作为初始聚类质心，随后按照特定的度量标准计算非质心点到聚类质心的距离，进行聚类划分。最后计算每个聚类的数据点到质心的平均距离，并依此调整质心，经过多次迭代计算，每个类簇中的样本点相似度较高，类簇间的相似度较低。

传统K-means算法过程如下：

输入：待聚类初始Dataset，聚类中心的初始质心个数K。

输出：聚类结果即K个类簇。

具体的算法步骤：

步骤1：从待聚类的初始Dataset中随机选择K个样本点作为初始聚类质心。

步骤2：计算非中心点到聚类中心的距离，将其分配到与自己最近的中心点。

步骤3：当所有点都归类完毕后，调整中心点：把中心点重新设置成该类别中所有数据点的中心位置，将每个类簇中的距离平均值作为新的聚类质心。

步骤4：根据每个非中心点到质心点的相似度(这里指距离越短相似度越大)对数据集进行重新聚类。

步骤5：重复步骤3，步骤4，直到类簇不再变化，或者达到设定的迭代次数即可结束算法。

传统K-means算法的主要缺点：时间复杂度为O(nkm)，其中n为原始数据集的个数，K为聚类中心个数，m为迭代次数。传统K-means算法时间复杂度高，随迭代次数m、类簇数k值、初始数据集的增加而增大，因此传统K-means算法在处理海量数据时综合性能较低。另外K均值算法过于依赖初始聚类中心点的选取，选择不同的初始聚类中心点，其最后的聚类结果也相差较大。

2.3 K-means++算法

因为标准的K-means分类结果会受到初始质心点的选取而产生差异，因此提出对传统K-means算法进行优化即K-means++算法，K-means++聚类算法主要是对初始质心点的选取进行改进，主要优化方法是初始的聚类质心之间的距离要尽量大，这样可以保证样本点会尽可能的分配到聚类中心中。

K-means++算法虽然能增加聚类准确率，但是没有减少冗余计算，而且在选取初始中心点增加额外计算以及第n个聚类质心的选择依赖于前n个聚类质心。

3 SMGK-means算法及在Spark上的并行化实现

3.1 改进K-means算法措施

通过形态学相似距离，最大距离距离准则以及建立聚类中心与数据点的位置关系来优化标准K-means算法。

3.1.1 形态学相似距离MSD

相似度测量标准一般由明可夫斯基距离推导出，主要应用有欧氏距离，曼哈顿距离。

定义1：明可夫斯基距离

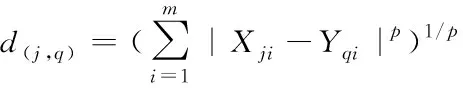
(1)

其中(1)式中：Yqi为向量q的第i个属性值，Xji是向量j的第i个属性值，m为向量维度，|Xji-Yqi|表示点与点再属性i上的距离。当p=2时，表示欧氏距离；p=1时表示曼哈顿距离。

定义2：形态学相似距离MSD(morphological similarity distance)

DMSD=(2-ASD/SAD)×ED

(2)

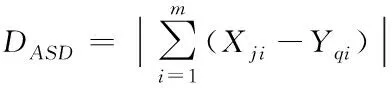
(3)

其中(2)式中：SAD表示曼哈顿距离，ED表示欧氏距离。(3)式表示两个向量属性差值之和的绝对值，Xji是向量j的第i个属性值，Yqi为向量q的第i个属性值m表示特征维度。表1表示了向量间的距离计算示例。

表1 向量间的距离计算

可以看出，若SAD/ASD=1，即ASD距离等于曼哈顿距离时，MSD距离就是欧式距离。

3.1.2 最大距离准则选择初始质心点

Max-distinece算法是由最大最小距离算法改进而来，根据其最大距离原则选取初始的聚类质心。

算法过程如下：

步骤1：从数据集中任意选取靠近边界点(不是边界点)，作为聚类质心C1，同时记C为聚类中心集合

步骤2：选择聚类质心C1最远的数据点作为第2个聚类质心C2；

步骤3：计算其它数据点与C1，C2之间的距离，并且计算出它们中的最小值，即式(1)、(2)

dxy=‖nx-ny‖，y=1，2

(4)

dx=min[dx1，dx2]，x=1，2，…n

(5)

步骤4：如果(θ为规定的参数)

dl=maxx[min[dx1，dx2] ]>θ*‖n1-n2‖

(6)

则相应的样本nl作为第3个聚类中心C3，然后继续判断next聚类质心；

步骤5：如果存在k(k！=K)个聚类中心，计算各个样本点到聚类质心的距离dxy，并计算出：

dl=maxx[min[dxy，dxz] ]>θ*‖ny-nz‖

(7)

其中y！=z且y，z∈C

步骤6：已经求出K个初始聚类中心点，将其保存记为C

3.1.3 数据集的空间位置信息减少冗余计算

为减少K-means算法冗余计算量，引入数据点与聚类中心的空间位置关系[11]，基本做法是，对于初始数据集中的任意点，若能知道它与K个类簇质心的空间位置关系，就可能判断出离它最近的聚类质心是哪一个，这样就无需执行k次计算，只需将数据点分配到相应的类簇中去。

如何建立数据集与聚类中心的空间位置信息，以三维数据为例，对于一个在空间直角坐标系任意数据点s(x，y，z)，假设x所在维度最大值为maxx，最小值为minx，网格在这一维上所划的分段数为xNum。假设y所在维度最大值为maxy，最小值为miny，网格在这一维上所划的分段数为yNum。假设z所在维度最大值为maxz，最小值为minz，网格在这一维上所划的分段数为zNum。根据数据集中点的坐标，可以按照式(8)，(9)，(10)快速定位点s的网格位置(x′，y′，z′)

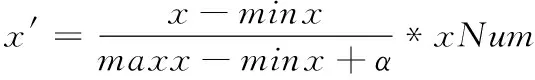
(8)

(9)

(10)

其中α为正的小数。

由上述数据点s所在网格与k个聚类质心的关系即可确定点s与类簇的关系，即点s所可能归属的聚类质心有哪些。那么就可以有效地减少点s与聚类质心之间的计算量。

3.2 肘部法则确定K值

对于肘部法则[12]确定类簇个数K而言，其中误差平方和SSE和距离度量标准如下

(11)

其中x，y表示不同的两个样本，n表示样本的维度即特征数量

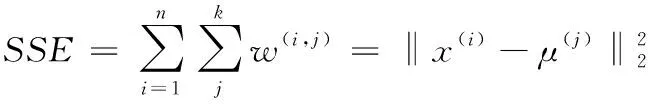
(12)

针对大规模数据可以利用肘部法则来确定类簇数K。肘部法则的计算思想是代价函数，代价函数是取类簇数为k时所求的SSE，若类簇内部的数据点之间越紧凑则SSE越小，反之，若内部的数据点之间越分散则SSE越大。在选择类簇个数而言，肘部法则会把不同k值聚类所得到的SSE画成关系图。随着k值的增大，SSE值就会越来越小，每个类簇中所包含的样本数会减少，数据点离其聚类质心会更近。但是，随着k值的增加，误差平方和SSE值下降的幅度就会变得缓慢。在k值上升过程中，SSE下降幅度最快位置所对应的值就是肘部。

3.3 算法改进步骤

在上述2.2节和2.3节中分析了K均值法和K-means++的主要缺点，下面对如何选择初始中心点，减少冗余计算量以及并行化提出了解决办法。首先此文中的测量距离据使用形态学相似距离MSD。优化算法的步骤如下：设原始数据集Dataset={x1，x2，x3，…，xn}，并且xi属于Rd，其中n为原始数据集的个数，xi表示为d维向量。先预设K值范围如[n1，n2]，依此取n1与n2之间的整数K；对于所取的每一个K值，首先根据Max-distance距离算法选择K个初始中心点；然后利用数据点与K个类簇中心的位置关系将数据点归属到与其最近的中心中，其次更新K个类簇中心和网格空间信息，重复此过程，直到簇类中心不再变化或者达到规定的迭代次数；最后处理得到对应K值的SSE，然后在直角坐标系中绘制K-SSE关系图，此图类似于手肘的形状，此时这个拐点所对应的k值就是数据集的实际聚类数即最优K值。

3.4 基于Spark的SMGK-means算法的并行实现

为了能有效地提高K-means算法的并行计算能力，本文提出了基于Spark的SMGK-means算法，主要是围绕ShuffleMapTask和ResultTask两个任务进行的。算法流程图如图3所示。

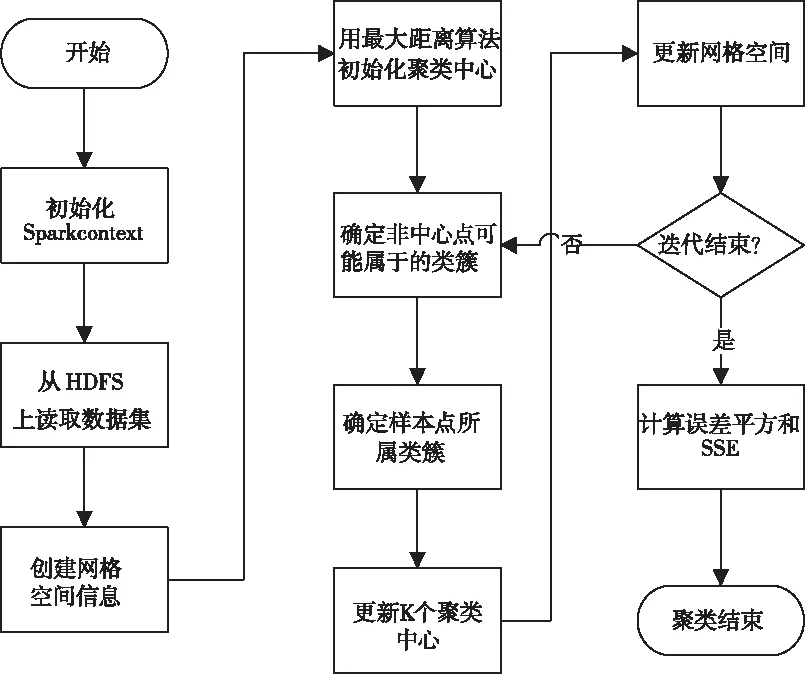
图3 基于Spark的SMGK-means算法

在每次迭代计算过程中，先对每个RDD分区进行mapPartitions操作，mapPartitions与map操作不同，是针对RDD中每个分区的迭代器，每次处理分区中的所有数据，且执行一次，提高了计算效率。之后对数据点进行聚类。通过数据坐标得到的对应网格，利用类簇和网格的关系确定数据点可能归属的类簇，最后从可能的聚类质心中查找最近的类簇，以此来减少冗余的计算。将所有点分配完成后，再将不同executor中的簇类中心进行reduceByKey操作汇总，得到新的K个聚类质心，同时对网格和类簇的空间关系进行更新。迭代结束后，通过肘部法则来确定最终的k值和类簇结果。

SMGK-means算法流程大致可以划分为以下数据分区，聚合和验证三个阶段。其算法代码如图4所示。

图4 程序代码

改进策略的要点如下：先使用MSD替换传统的距离度量如欧式距离，然后利用最大距离准则选择最优的初始中心点，提高K-means算法的全局搜索能力。其次使用网格结构保存数据点与聚类中心的空间位置关系，得到数据点所归属的可能类簇。最后利用Spark框架中的广播变量，把K个中心点所组成的集合广播到集群中每个节点的executor进程中，然后进行相应的算子操作，从而减少数据点在节点中的移动次数。通过以上改进策略能很好得提高算法的效率和性能。

3.5 每个K值下SMGK-means算法时间复杂度分析

改进的算法时间复杂度得到明显的降低，如果合理的选择网格划分宽度，能在很大程度上保证绝大多数网格都只会属于一个聚类中心，只有少量网格的可能归属类簇为两个及以上。因此对于大多数的数据点都只需执行一次距离计算，而非K次。若排除选取初始聚类质心所消耗的时间，SMGK-means算法的时间复杂度为O(nm)，其中n为数据点个数，m为迭代次数。

4 实验及结果分析

本文基于Spark分布式集群实现SMGK-means算法，实验环境由五台虚拟机组成，其中包括一台master主节点，负责driver程序的运行和管理，剩下四台work从节点作为执行节点。

硬件配置：每台虚拟机CPU双核1.8GHz，内存2GB，磁盘容量20GB。操作系统是64位的Ubuntu16.04。

软件配置：每台虚拟机上装有jdk1.8.0＿191，scala-2.11，hadoop-2.9.1，spark-2.4.3。采用具有面向对象风格和函数式编程特性的Scala语言，同时为验证SMGK-means算法的有效性，采用Spark ML[13]中标准K-means算法、K-means++算法以及文献[14]中算法作为对比试验。测试数据集为UCI数据集库中的abalone，Aggregation，glass三种不同量级的数据样本。为了方便验证实验，对相关数据集进行预处理(删除和增加相应的数据)，处理后数据集如表2所示。

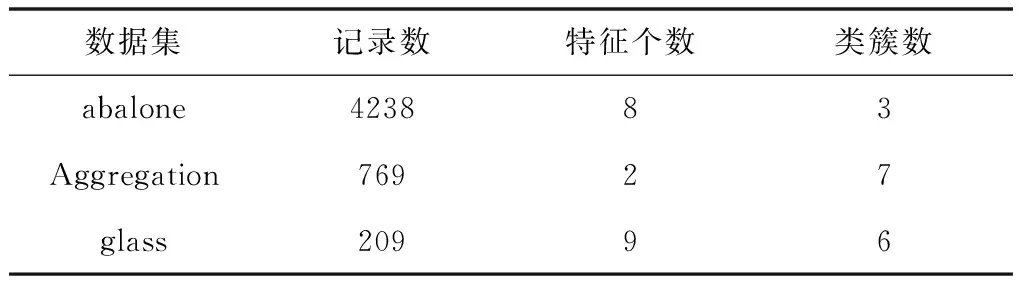
表2 数据集

针对上述三种数据集，修改数据集中每条记录的聚类中心，然后提取其中的特征另存为train.txt上传到HDFS上，随后模型读取的数据就是HDFS上的train.txt。实验结束所保存的数据也在HDFS上。

1)算法运行时间比较。本文利用执行时间衡量SMGK-means算法执行效率。图5是上述四种算法在不同数据集的执行时间，可以看到SMGK-means算法比另外三种算法减少了聚类时间。因为SMGK-means算法采用网格表示数据点与聚类质心的位置关系，降低聚类计算的次数，提升了收敛速度；同时利用spark中broadcast将每次更新的中心点广播到各个执行节点中，将作业粒度转变成节点粒度，执行节点每次从本地内存中读取聚类中心，节省执行节点间的通信开销。图6比较并行环境下不同数据集在不同数量节点上使用SMGK-means算法的聚类时间，体现出随节点worker的增加，SMGK-means算法的运行时间逐渐减少，最后趋于平缓。平缓的原因是由于worker间的通信开销抵消了并行化带来的增益。

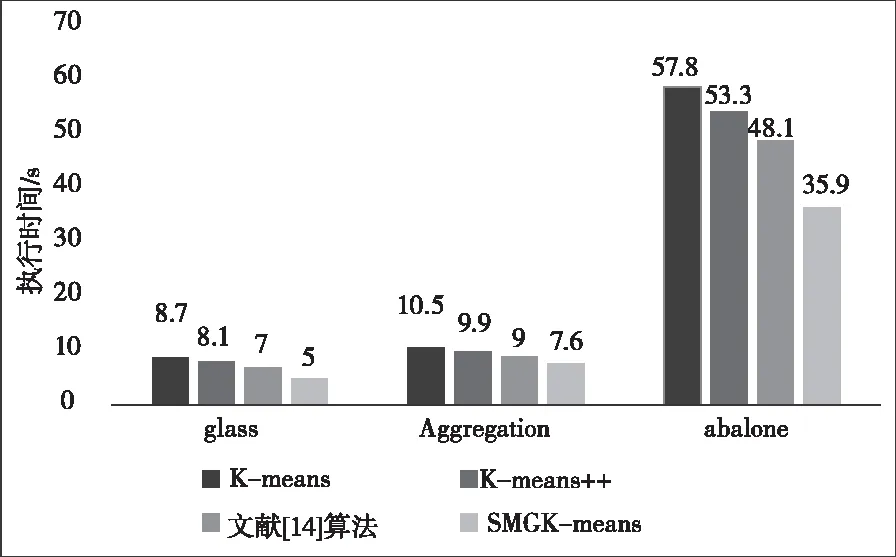
图5 4个节点下各算法的运行时间

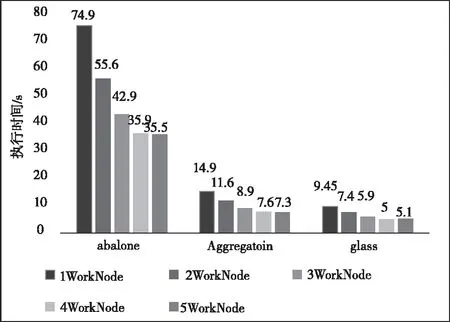
图6 不同节点个数SMGK-means算法所消耗的时间

2)准确率对比。算法准确率指类簇划分正确记录的个数与数据集中总记录个数的比值。表3给出三种不同的数据集在五个节点下，SMGK-means算法与K-means、K-means++以及文献14算法的准确率。由表3可知本文的SMGK-means算法相比于其它三种算法准确率有显著的提高。因为SMGK-means算法利用最大距离算法、网格空间结构优化了标准K-means算法，提高了全局搜索能力。

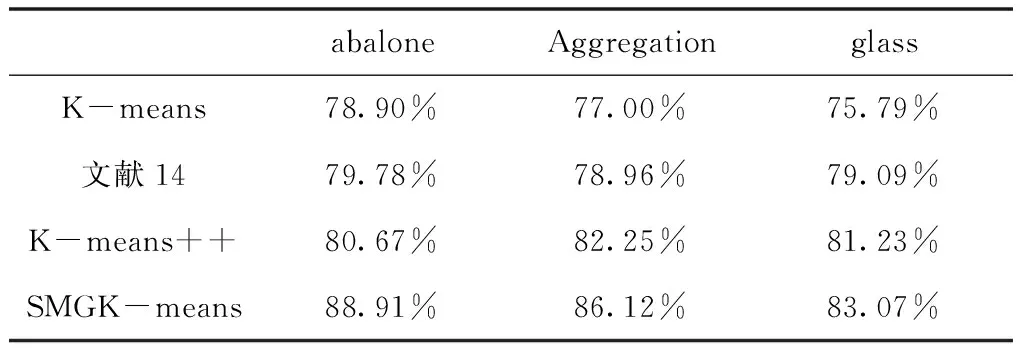
表3 SMGK-means与其它三种算法的准确率

3)加速比的对比。算法加速比[15]是衡量程序性能、并行性能的重要指标。其定义是同一个job在并行中与串行中执行时间比值的倒数，计算公式为Rate=Js/Jp，其中Js为单机下的运行时间，Jp为分布式集群下执行时间，Rate越大表示算法在单机环境下执行时间越大，在分布式集群下运行时间越小。为验证SMGK-means算法并行性能，实验依然是基于上述三种不同量级的数据集，图6给出三种不同数据集在不同节点个数下的运行时间。得到SMGK-means算法加速比如图7所示。从图7横向比较得到SMGK-means算法的加速比随执行节点个数增加而增加。但随着节点个数的增加，其加速比趋于平缓，其原因是节点之间的通信开销。纵向比较得在相同节点个数下，随记录个数的增加，其加速比也随之增大。

图7 基于SMGK-means的加速比

4)手肘法确定K值。上述1)2)3)的对比实验结果均是在K最优情况下进行的，而对于K值未知的数据集利用手肘法确定K值。先预测最优K值范围，每取K值执行一次SMGK-means算法，即可得到类簇内的数据点到其簇类中心的距离平方和SSE，并绘制K与SSE的关系图；然后利用肘部法则确定K值和对应的聚类结果。图8表示数据集alalone的K与SSE的关系图，由图8可知，随K值不断逼近真实类簇数时，SSE的下降趋势加快，而当设定的K值超过实际类簇数时，SSE下降态势会趋于缓慢。K-SSE的关系图中的拐点即为最优的K值，与表1数据集中alalone的类簇数相同。

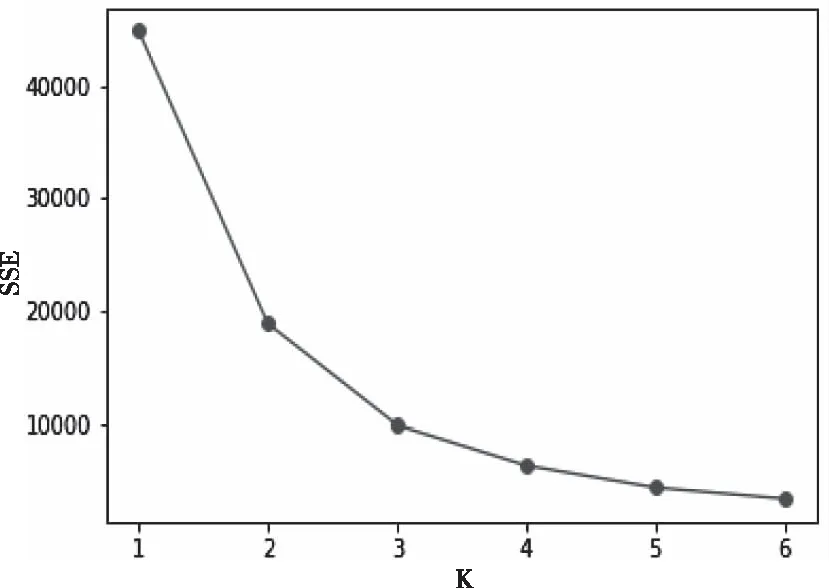
图8 K与SSE的关系图

综合1)2)3)得到，SMGK-means算法与上述三种算法相比减少了执行时间，且其准确率平均提高了6.73%；从加速比上分析SMGK-means算法具有良好的并行计算性能；而对于无法提前确定K值的数据集利用肘部法则也能得到正确的聚类簇数。故总体而言本文的SMGK-means算法相较于其它三种算法有了较大的提升。

5 结语

本文针对标准K-means算法的初始中心点选择和冗余计算等问题，提出SMGK-means算法。此算法以MSD为相似度度量标准，利用最大距离算法优化初始中心点选取，采用网格数据结构保存数据点位置关系，减少冗余计算。通过手肘法确定最优K值。实验表明SMGK-means算法显著提高了聚类的准确率，减少了执行时间，且在分布式集群下有较高的性能。在下一步研究中，笔者准备提高数据集和集群规模，以此验证SMMK-means算法的鲁棒性。