城市轨道交通列车追踪及折返运行研究
张 海,倪少权,邹葱聪
(1. 西南交通大学交通运输与物流学院,四川 成都 610031;2. 综合交通运输智能化国家地方联合工程实验室,四川 成都 610031;3. 综合交通大数据应用技术国家工程实验室,四川 成都 610031)
1 引言
随着城市轨道交通客流量不断增大,部分城市高峰时段线路运营能力已满足不了客流需求。线路运营能力通过列车追踪间隔体现。列车追踪间隔由区间追踪间隔、中间站通过间隔及折返站折返间隔组成。根据现有文献[1,3-5,7] 及城市轨道交通线路实际运营情况,折返间隔是限制城市轨道交通线路运营能力的重要制约因素。
目前对折返间隔的研究主要是利用图解法与解析法这两种方法。图解法将列车在折返过程中每一项作业所消耗的时间按作业顺序绘制在作业图上,从而找出相邻两列车的间隔时间。解析法通过分析列车折返作业过程及影响因素,建立计算折返间隔时间的数学关系式。王珮瑶[1]以几种有代表性的折返站型为例,解析了折返作业过程,得出折返间隔计算公式。李娜[2]从折返站配线角度分析了折返间隔影响因素,计算了不同折返站配线形式下的折返间隔。鲁秋子[3]利用图解法分析了安全距离长度对折返间隔的影响。张帅[4]分析了折返间隔组成时间,对折返间隔影响因素进行了定量分析。王俊锋[5]利用图解法计算站后单线折返与双线折返间隔,提出了缩短折返间隔的措施。李琼[6]解析了站前单股道折返与双股道折返技术作业过程,利用图解法进行了折返能力影响因素分析。徐意[7]通过分析列车在折返过程中需遵守的限制条件,推导出了折返间隔与折返时间及停站时间之间的相互关系。
移动闭塞模式下列车运行受到前行列车实时影响,列车之间追踪运行须满足最小追踪距离要求。既有对折返间隔的研究基于单列车,只考虑了单列车的折返运行,没有考虑多列车的追踪及折返运行情况,不能反应线路上所有列车实际运行情况,不能体现交通流细节。本文建立基于多列车的列车追踪及折返运行模型,模拟线路上所有列车追踪及折返运行情况,定量分析折返间隔与追踪间隔对线路运营能力的影响,为城市轨道交通列车时刻表编制及列车运营管理提供理论依据。
2 列车追踪及折返运行描述
图1为某城市轨道交通线路及信号配置示意图。车站1为普通车站,车站2为折返站,列车利用车站2站前折返线进行折返作业。列车从车站1下行站台停车点A出发,沿车站1与车站2站间区间BC运行,在车站2完成折返并驶离车站2上行站台,列车尾部出清计轴点N完成折返作业。
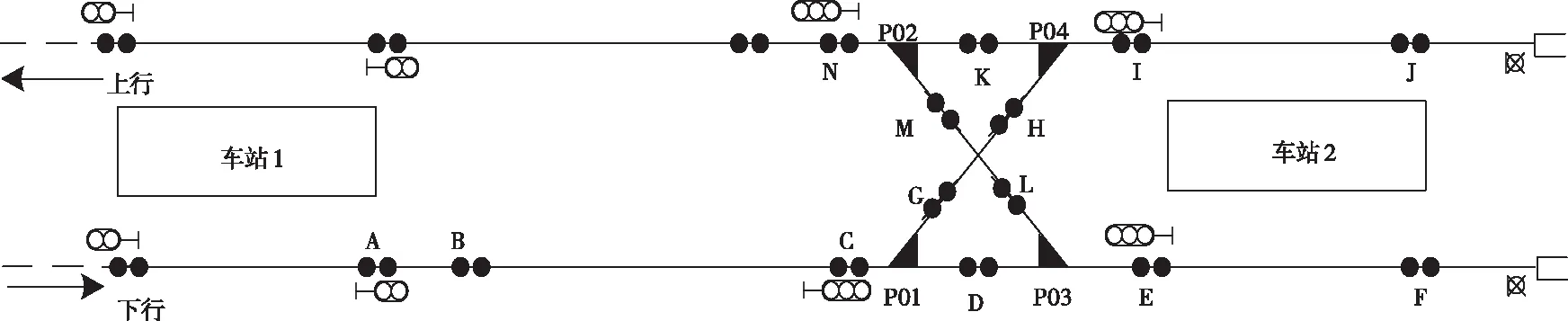
图1 轨道线路及信号配置图
2.1 列车在区间追踪运行场景
列车在追踪运行过程中,需满足移动闭塞最小追踪距离要求[8]
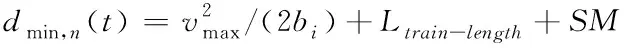
(1)
式中dmin,n(t)为移动闭塞模式下第n列车与前方列车最小追踪距离;vmax为列车最大允许运行速度;bi为列车减速度;Ltrain-length为列车长度(包含车钩);SM为安全余量,安全余量取值需综合考虑信号系统反应时间、车辆制动系统反应时间及建立有效制动力所需时间。
在移动闭塞模式下,列车速度及在线路上的位置通过无线通信系统实时传输给轨旁ATP计算机,轨旁ATP计算机根据相关列车的位置及速度信息计算出每列车的移动授权并实时传输给列车。移动授权计算原则为:若追踪列车与前方列车的实际距离小于最小追踪距离则列车减速,若追踪列车与前方列车的实际距离大于最小追踪距离则列车加速,否则列车保持速度不变。移动授权每个时间步长更新一次。
2.2 列车折返运行场景
如图1所示线路,车站2站前配置有两组交叉渡线。由于列车在进站过程中需要减速以满足站台限速要求,为提高运营效率,在实际运营过程中采用侧进(P01-P04)直出(P04-P02)的方式进行折返。只有在相关设备故障时,临时情况下采用直进(P01-P03)侧出(P03-P02)的方式进行折返。正常运营情况下列车侧进直出折返过程如下所述。
Step1:当前行列车出清计轴点N后,道岔P01、P04转向侧位。在进路C-J排列好后,列车越过信号机C,通过交叉渡线P01-P04驶入车站2上行站台,停在上行站台停车点J。
Step2:列车在车站2停站期间进行上、下客
作业,完成自动换端,排列出站进路I-N。
Step3:停站时间结束后,列车从车站2上行站台出发,待列车车尾出清计轴点N,完成折返过程。
3 列车追踪及站前折返模型
本模型将列车运行路径划分为相邻的轨道区段,在每个轨道区段内根据相应的运行规则更新列车的速度及位置信息,每个时间步长列车信息更新一次。
模型边界条件:从车站1下行站台停车点A每隔发车间隔Tdeparture-int erval发出1列车。列车从车站1出发,经过区段BC后通过交叉渡线P01-P04驶入车站2上行站台。停站时间结束后列车驶离车站2上行站台,列车尾部出清计轴点N即驶离系统。
Step1:列车在区段A-B运行。列车运行规则及约束条件如下。
1)在列车开始运行到车尾出清计轴点B的过程中,列车速度不能大于站台限速。
If{vn(t)<=vplatform}:
vn(t+Δt)=min{vn(t)+ai×Δt,vplatform}
Elsevn(t)=vplatform
(2)
式中vn(t)为t时刻第n列车的速度;vplatform为站台限速;Δt为步长;ai为列车加速度。
2)相邻列车追踪距离须满足最小追踪距离要求。若列车与前车追踪距离小于最小追踪距离则减速,若大于最小追踪距离则加速,否则速度不变。
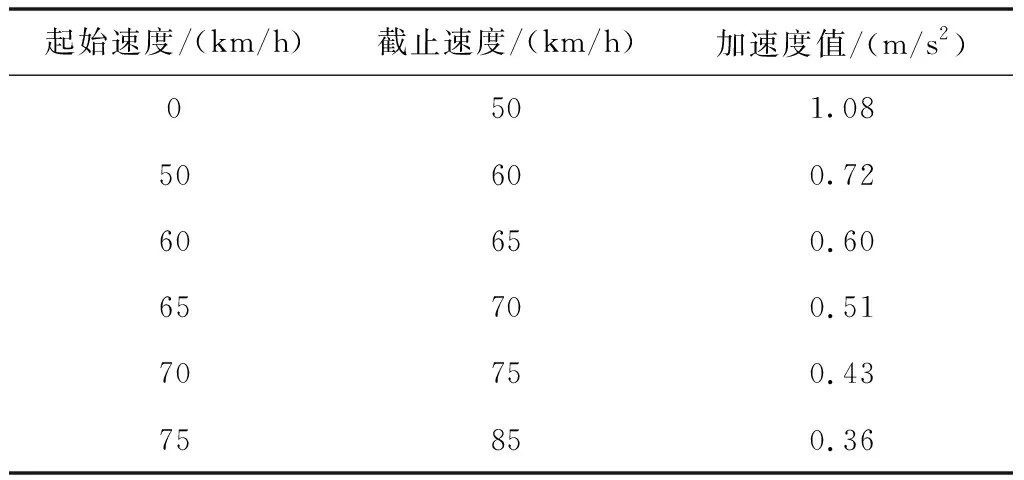
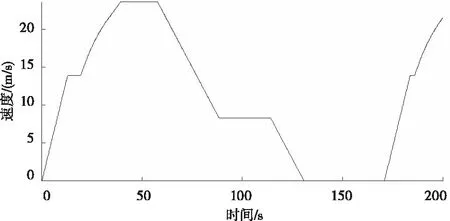
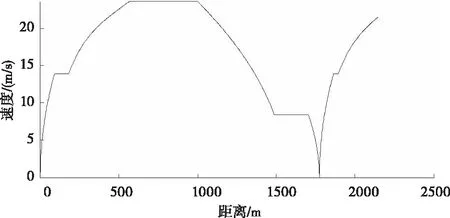
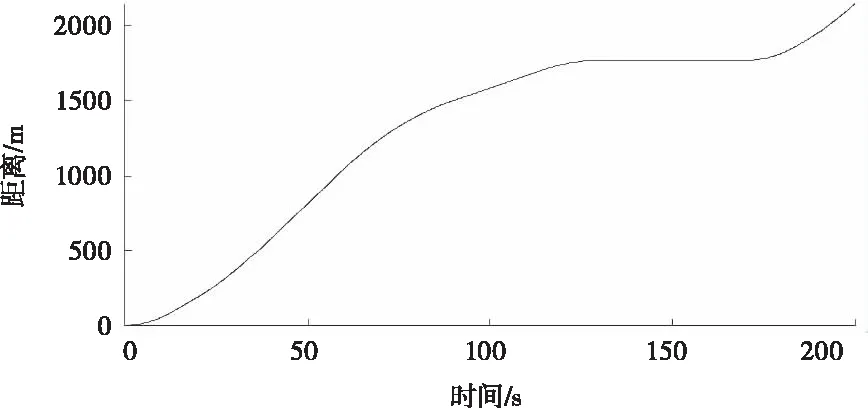
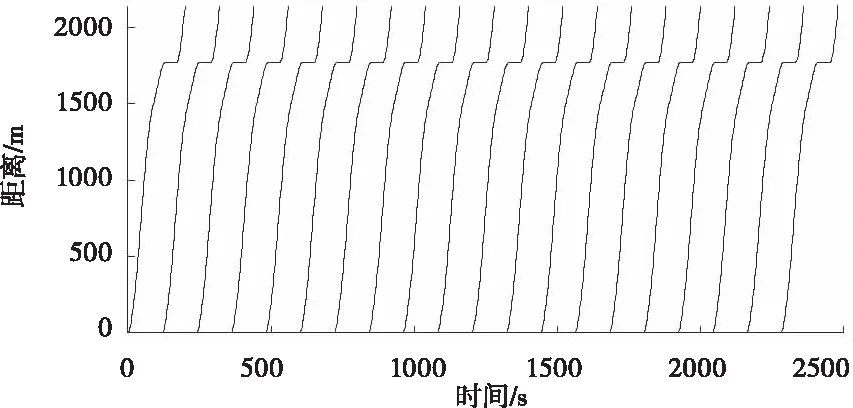
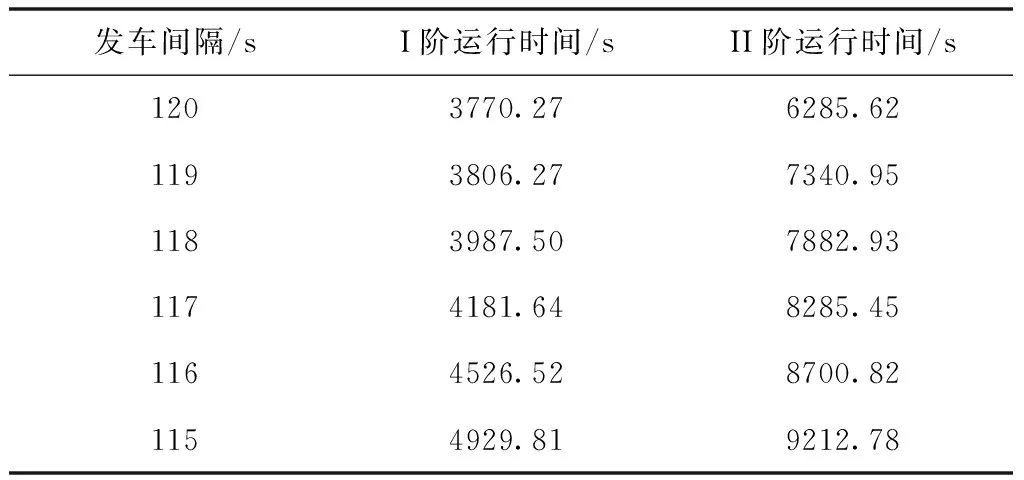
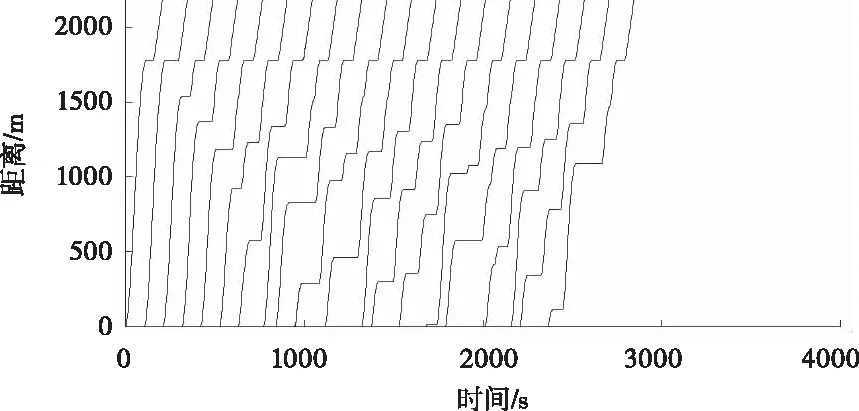
If{dn(follow)(t) vn(t+Δt)=max{vn(t)-bi×Δt,0} If{dn(follow)(t)>dmin,n(t)}: vn(t+Δt)=min{vn(t)+ai×Δt,vmax} Elsevn(t+Δt)=vn(t) (3) 式中dn(follow)(t)为t时刻第n列车与前方列车的距离;dmin,n(t)为t时刻第n列车与前方列车最小追踪距离,见式(1);bi为列车减速度;ai为列车加速度;vmax为列车最大运行速度。 Step2:列车在区段B-P01运行。列车运行规则及约束条件如下。 1)列车到达P01时速度应不大于道岔侧向限速。 If{dP01(n)(t)>dbP01(n)(t)}: vn(t+Δt)=min{vn(t)+ai×Δt,vmax} Elseif{dP01(n)(t)<=dbP01(n)(t)}: vn(t+Δt)=max{vn(t)-bi×Δt,0} (4) (5) 式中dP01(n)(t)为t时刻第n列车到前方限速点P01的距离;dbP01(n)(t)为t时刻第n列车从当前速度降到道岔限速所需的制动距离;vswitch为道岔侧向限速。 2)相邻列车追踪距离满足最小追踪距离要求,见式(3)。 3)前行列车尾部出清计轴点N后,P01、P04道岔开始转向侧位,道岔转换完成后进路C-J开放。即:后续列车必须在P01、P04道岔转换完成且进路C-J开放后才能越过信号机C;否则后续列车必须在信号机C前停下来,待进路C-J开放后才能越过信号机C继续运行。 If{dN(n)(t)>dn(follow)(t)+Δs>dC(n)(t)}: vn(t+Δt)=max{vn(t)-bi×Δt,0} (6) Δs=vn(t)×Tswitch-change (7) 式中dN(n)(t)为t时刻第n列车到前方计轴点N的距离;dC(n)(t)为t时刻第n列车到前方信号机C的距离;Tswitch-change为道岔转换时间。 Step3:列车在区段P01-J运行。列车运行规则及约束条件如下。 列车运行过程中速度不能大于道岔限速,且必须在车站2上行站台停车点J停下来。 If{dJ(n)(t)>db(n)(t)}: vn(t+Δt)=min{vn(t)+ai×Δt,vswitch} Elseif{dJ(n)(t) vn(t+Δt)=max{vn(t)-bi×Δt,0} Elsevn(t+Δt)=vn(t) (8) (9) 式中dJ(n)(t)为t时刻第n列车到停车点J的距离;db(n)(t)为t时刻第n列车从当前速度减速到0所需的制动距离。 Step4:列车停在车站2上行站台。列车运行规则及约束条件如下。 列车在车站2上行站台停站期间进行上、下客作业、完成自动换端、排列出站进路I-N。停站时间为Tdewell-time,停站期间列车速度为0。自动换端结束后列车车头位置由J变为I(IJ长度为列车长度)。 Step5:列车在区段I-K运行。列车运行规则及约束条件如下。 列车从车站2上行站台停车点I出发到车尾出清计轴点K的整个运行过程中,速度不能大于站台限速,见式(2)。 Step6:列车在区段K-N运行。列车运行规则及约束条件如下。 在列车车尾出清计轴点K到车尾出清计轴点N的运行过程中,列车加速行驶,若达到最大运行速度vmax,则以最大运行速度运行。列车车尾出清计轴点N时驶离系统。 If{vn(t)<=vmax}: vn(t+Δt)=min{vn(t)+ai×Δt,vmax} Elsevn(t)=vmax (10) 列车在上述各个轨道区段运行过程中,每隔单位步长时间运行距离更新一次。列车距离更新如式(11)所示。 xn(t+Δt)=xn(t)+vn-average(t)×Δt vn-average(t)={vn(t)+vn(t+Δt)}/2 (11) 用Matlab软件编制程序,对某城市轨道交通线路(图1所示)列车追踪及折返运行情况进行仿真。仿真所用参数采用线路及列车实际参数。轨道线路按线路实际长度取值;安全余量SM=60m;停站时间Tdewell-time=40s;道岔转换时间Tswitch-change=10s;列车最大允许速度vmax=85km/h;道岔侧向限速vswitch=30km/h;站台区域限速vplatform=50km/h;列车减速度bi=0.5m/s2;列车加速度ai取值如表1所示。 表1 列车加速度值 步长Δt=0.01s,模拟列车数为50。在Inter(R)Core(TM)i3-9100CPU3.60GHz处理器、8.00GB内存、Windows1064位操作系统的计算机上,MatlabR2019b程序运行时间为8.78s;模拟列车数为100,程序运行时间为16.87s。 程序运行过程中同步绘制出列车运行曲线。 图2为列车运行的时间-速度图,图3为列车运行的距离-速度图,图4为列车运行的时间-距离图。图2~图4勾勒出列车时空运行轨迹:列车从车站1下行站台停车点A出发,从零速开始加速行驶,直至速度达到站台限速vplatform并匀速运行一段时间。列车尾部出清站台区域后,继续加速到最大允许速度vmax并以最大允许速度匀速运行。列车在进入车站2交叉渡线前开始减速,经过交叉渡线道岔P01时速度降为道岔限速vswitch,之后维持道岔限速匀速运行一段时间。列车在进入车站2站台区域时开始减速,直至停在车站2上行站台停车点J。在车站2上行站台停站时间结束后,列车从零速开始加速出站,直至速度达到站台限速并维持站台限速匀速运行一段时间。列车尾部出清站台区域后继续加速,直至驶离系统,完成折返过程。图2~图4仿真结果与列车实际运行情况完全一致,本模型可以反应列车实际追踪及折返运行情况。 图2 时间-速度图 图3 距离-速度图 图4 时间-距离图 图5显示的是发车间隔为120s时,前20列车追踪运行的时间-距离图。从图5可以看到后续追踪列车运行不受前行列车干扰;前20列车的距离-速度图完全一致,每列车的距离-速度曲线重合,如图3所示。 图5 时间-距离图(发车间隔为120s) 缩短发车间隔,当发车间隔为119.25s时,全线所有列车刚好不受其前行列车影响,因此列车在车站2的折返间隔为119.25s。 利用传统的图解法及解析法可计算出列车在车站2的折返间隔为116s。在项目现场进行的折返间隔极限能力测试,测出列车在车站2实际折返间隔为121s:利用本模型得出的折返间隔比传统方法得出的数值更为精确,与实际折返间隔仅相差1.45%。 由上可知,节3建立的列车追踪及站前折返模型能够反应列车实际追踪运行情况,仿真精度较高,可用于城市轨道交通列车追踪及折返运行研究。 在列车实际追踪运行过程中,当列车发车间隔过小时,由于相邻列车追踪间隔须满足最小追踪距离要求,会导致后续列车被迫在区间停车。表2所示为不同发车间隔情况下,仿真得出的列车运行数据。表2中“I阶运行时间”为第30列车驶离系统的时间;“II阶运行时间”为第50列车驶离系统的时间。 表2 不同发车间隔下列车运行时间 从表2可知,当发车间隔小于折返间隔时,随着发车间隔时间不断减小,列车延迟程度不断加大。发车间隔由120s减小为115s时,前50列车累计延迟时间为2927.16s,每列车平均延迟时间为58.54s。 图6为发车间隔为105s时,前20列车的时间-距离图:从第3列车开始发生明显延迟,列车被迫在区间停车。随着发出列车数量逐渐增多,列车交通流表现出明显的延迟传播现象,且后续列车延迟时间不断增大。 图6 时间-距离图(发车间隔为105s) 基于上述列车延迟传播的交通现象,考虑到城市轨道交通列车实际追踪运行时存在偶发的人为因素干扰或设备故障的实际情况,在制定列车运行时刻表时,列车在起始站的发车间隔应大于折返间隔,且留有一定余量以应对列车故障、线路故障等突发情况。 本文建立了基于移动闭塞的城市轨道交通列车追踪及站前折返模型,模拟线路上多列车的追踪运行情况。 1)仿真结果表明该模型能够真实、准确地反应线路上列车实际追踪运行情况,可以用于列车追踪及折返运行方面的研究。 2)利用该模型得出的折返间隔与列车实际折返间隔相差1.45%,优于传统的折返间隔计算方法。 3)当发车间隔小于折返间隔时,出现列车延迟传播的交通现象,且发车间隔越小,列车延迟现象越严重。发车间隔由120s减小为115s时,每列车平均延迟时间达58.54s。因此,在制定列车运行时刻表时,起始站的发车间隔应大于折返间隔,且留有一定余量以应对突发情况。 后续需利用本文建立的模型对折返间隔影响因素进行定量分析,提出缩短折返间隔、提高运营效率的具体措施。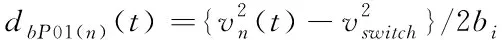
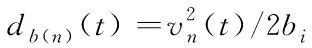
4 实例分析
4.1 仿真结果
4.2 列车延迟传播交通现象
5 结论

