带前级DC/DC的无线充电系统建模与分析

付琳琳，逄海萍

(青岛科技大学自动化与电子工程学院，山东 青岛 266100)

1 引言

磁耦合谐振式无线电能传输(magnetic-coupled resonant wireless power transmission，MCR-WPT)，具有传输距离远、效率高以及功率大等优点[1]-[2]，在无线充电领域有良好的应用前景。在无线充电过程中，需要根据电池荷电状态控制从电网侧流向电池的功率，目前功率控制的方式主要有原边逆变器的移相控制、变频控制以及前级附加DC/DC控制等。

移相控制可以方便地通过调节逆变器的移相角实现蓄电池的恒压或恒流充电[3]-[4]，但逆变输出电流会随移相角的变化发生不同程度的畸变，并且不能实现逆变器在整个充电过程中的零电压开关(zero voltage switch， ZVS)。变频控制通过调节逆变器的工作频率来调节充电电压或电流[5]-[6]，可以实现逆变器的ZVS，但工作频率偏离谐振频率，会使系统的传输效率降低。前级附加DC/DC控制是在逆变器之前添加DC/DC变换器，通过调节DC/DC变换器的占空比来获得稳定的充电电压或电流，控制精度较高，且能够实现逆变器在整个充电过程中的ZVS。相比于前两种方式，后者在整个功率调整范围内的效率是最高的[7]-[8]。

准确数学模型是进行系统分析和系统设计的基础，而对于带前级DC/DC的MCR无线充电系统，由于系统含有DC/DC变换器、高频逆变器以及高频整流器等多种非线性开关电路并且MCR电路工作在谐振状态，具有高阶次、变结构、非线性等特点，使其准确数学模型的建立变得复杂和困难。

本文首先对带前级DC/DC的MCR无线充电系统的结构及特点进行分析，然后用状态空间平均法(state space average，SSA)和广义状态空间平均法(generalized state space average，GSSA)分别对不同的非线性单元进行建模，并最终获得系统的数学模型。通过Matlab软件对系统模型进行验证，并对系统的稳定性及控制特性进行分析。

2 系统结构与动态建模

2.1 系统结构及特点

带前级DC/DC的MCR无线充电系统如图1所示。系统由DC/DC单元、MCR-WPT单元、电池负载三部分组成。其中电池负载用可变电阻负载来代替。

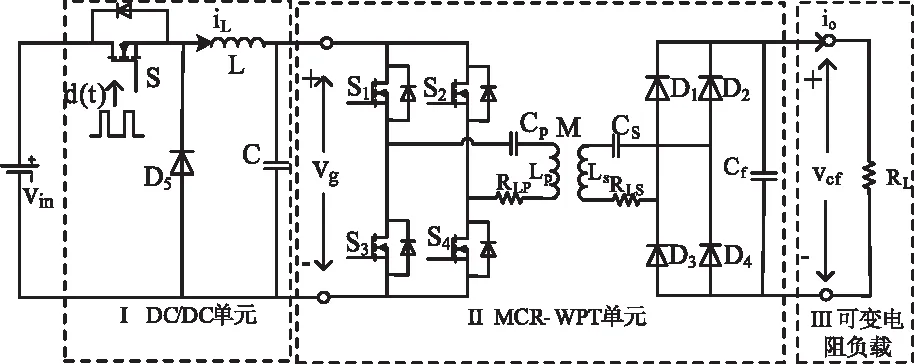
图1 带前级DC/DC的MCR无线充电系统图

设vin是工频交流通过整流得到的不可控直流电源，DC/DC单元在此采用Buck结构，通过调节开关管S的占空比改变高频逆变器直流母线电压vg，从而实现终端负载的电压和电流控制。在Buck输出端接有电容C以减小Buck开关过程对逆变器的影响，同时为逆变器提供稳定的输入电压。

MCR-WPT单元中，四个MOSFET管S1～S2构成高频逆变器，开关S1、S4与S2、S3交替导通和关断，逆变器输出正负交替的矩形波，当原边发射回路处于谐振状态时开关管可以实现ZVS通断。Lp、Cp与Ls、Cs分别构成原、副边串联补偿磁耦合谐振网络，M为发射线圈和接收线圈之间的互感系数，RLp与RLs分别这两个线圈的内阻。假设原、副边的电感电容参数一致，两侧电路以相同频率谐振，经磁场耦合完成能量传递。D1～D4构成高频整流电路，接收线圈获得的交流电经过整流及电容Cf滤波后向负载RL供电。

系统中含有Buck开关变换器和MCR-WPT串联谐振开关变换器，很难直接对其统一建模。Buck与其后级的谐振开关变换器之间接有电容C，该电容除了具有滤波稳压的作用外，还可以实现前后两类变换器之间的解耦，因此可以将两级单元分开建模。

前级Buck单元只含直流变量，电感电容的自然频率远低于其开关频率，使用SSA法建立其小信号模型[9]。MCR-WPT单元中的谐振网络会产生交流变量，SSA法不再适用。GSSA是利用有限阶的傅里叶级数之和将周期系统的状态变量近似线性化，能准确描述状态变量的暂态和稳态行为[10]-[11]，因此本文采用GSSA法对MCR-WPT单元建模。

2.2 DC/DC单元的建模

设Buck变换器中开关管S的开关周期为Ts，开关频率fs=1/Ts，S导通的占空比为d(t)，将MCR-WPT单元与电阻负载RL看作一个等效电阻R，并将R作为Buck变换器负载。Buck变换器的开关周期平均模型是非线性模型[12]，设变换器在某一稳态工作点处各变量d(t)、vin(t)、iL(t)、vC(t)及vg(t)的稳态值分别为D、Vin、IL、VC及Vg，根据状态空间平均法得到它的小信号模型

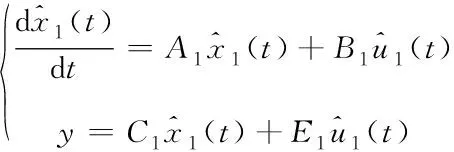
(1)

由(1)可求得Buck变换器输出电压-输入电压传递函数Gvgvin(s)和输出电压-占空比传递函数Gvgd(s)分别为

(2)

(3)

2.3 MCR-WPT单元的建模

假设MCR-WPT单元的开关均为理想开关，逆变器的开关周期为Td，开关频率fd=1/Td，且与发射回路和接收回路的固有谐振频率fc相同。将MCR-WPT单元简化为图2所示的等效电路。

图2 MCR-WPT单元的等效电路图

图2中iLp为逆变器输出电流，iLs为整流桥输入电流。对于系统中非线性原边逆变环节和副边整流环节，分别采用开关函数p(t)和s(t)表示它们的能量变换关系。在Simulink中对系统仿真可知逆变器输出电压p(t)vg与整流桥输入电压s(t)vcf的相位相差1/4个周期，即函数p(t)和s(t)的相位差为90°，则p(t)和s(t)的表达式分别为

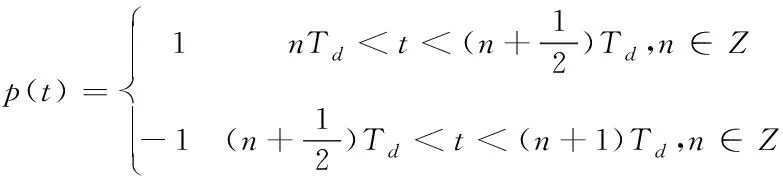
(4)

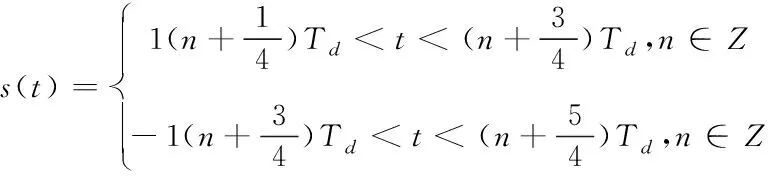
(5)

选取原边电容电压vcp，原边电感电流iLp，副边电容电压vcs，副边电感电流iLs，输出电压vcf作为状态变量，根据KCL、KVL得到时域微分方程

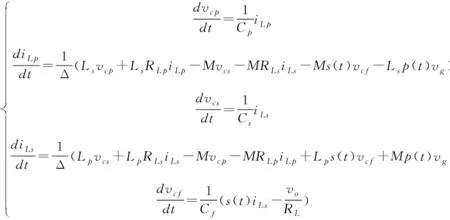
(6)

其中，△=M2-LpLs。

方程组(6)是非线性的，对其求解非常困难，在此采用GSSA方法将原始信号用共轭低阶谐波分量来近似，并利用傅里叶级数相关性质对非线性环节进行近似线性化[13]。

周期为T的连续变量x(t)傅里叶级数的指数展开形式为

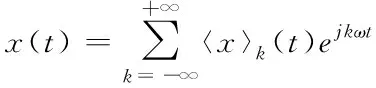
(7)

其中，ω=2π/T为x(t)基波角频率，〈x〉k为k次傅里叶系数，且

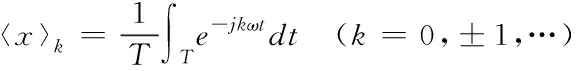
(8)

根据式(8)求得开关函数p(t)和s(t)的k阶傅里叶系数分别为

(9)

(10)

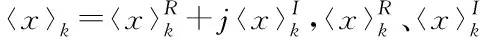
由式(11)可以得到变量x(t)的时域表达式。

状态变量vcf为直流变量，采用零次谐波分量〈vcf〉0来代表其特性；状态变量vcp、iLp、vcs、iLs为交流变量，零次谐波分量近似为零，且奇次谐波分量共轭对称，在谐振状态下，具有良好的正弦特性，因此，只考虑它们的1阶傅里叶级数〈vCP〉1、〈iLP〉1、〈vcs〉1、〈iLs〉1即可。

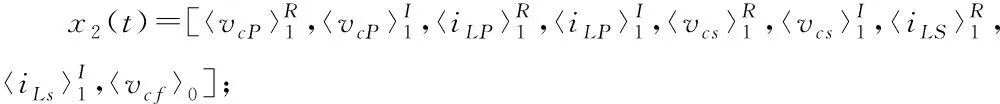
(12)

其中，

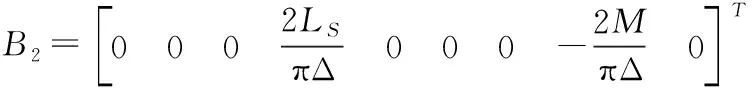
E2=[0]

可以看出，式(12)是一个9阶的线性方程，且方程的系数与单元参数相关，一般情况下，当元件选定后，原、副边的电感电容值在运行过程中变化很小，但线圈间距离或者负载值的变化会导致方程系数的改变。

由(11)可推导出MCR-WPT单元的输入电压到输出电压的传递函数：

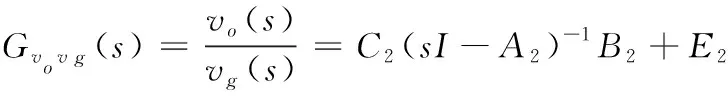
(13)

2.4 系统的数学模型

前级Buck单元的输出即为后级MCR-WPT单元的输入，即u2(t)=y1(t)，将两级单元模型串联到一起，整个系统模型框图可由图3表示：

图3 系统模型框图

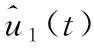
(14)

Gvod(s)=Gvovg(s)Gvgd(s)

(15)

3 模型的仿真验证与分析

3.1 仿真参数

利用Matlab软件对系统数学模型进行仿真验证，具体参数为： 输入电压vin=40V，Buck电感L=1.5mH，Buck电容C=65nF，Buck等效负载R=7.5Ω，Buck开关频率fs=100kHz，谐振频率fc=85kHz，原、副边谐振电感Lp=Ls=116.86μH，其内阻RLp=RLs=0.5Ω，谐振互感M=18μH，原、副边谐振电容Cp=Cs=30nF，滤波电容Cf=10μF，系统负载RL=20Ω。

3.2 模型的仿真验证

为验证所建系统数学模型的准确性，在Simulink下搭建系统的拓扑模型，如图4所示，并与由所建数学模型得到的变量时域运动轨迹进行对比。在数学模型(14)中，Buck单元的电感电流、输出电压以及负载输出电压为直流变量， MCR-WPT单元原、副边的谐振电压与电流为交流变量，且交流变量的运动行为相同，在模型验证只取原边电容电压进行分析。

图4 基于系统拓扑模型的仿真图

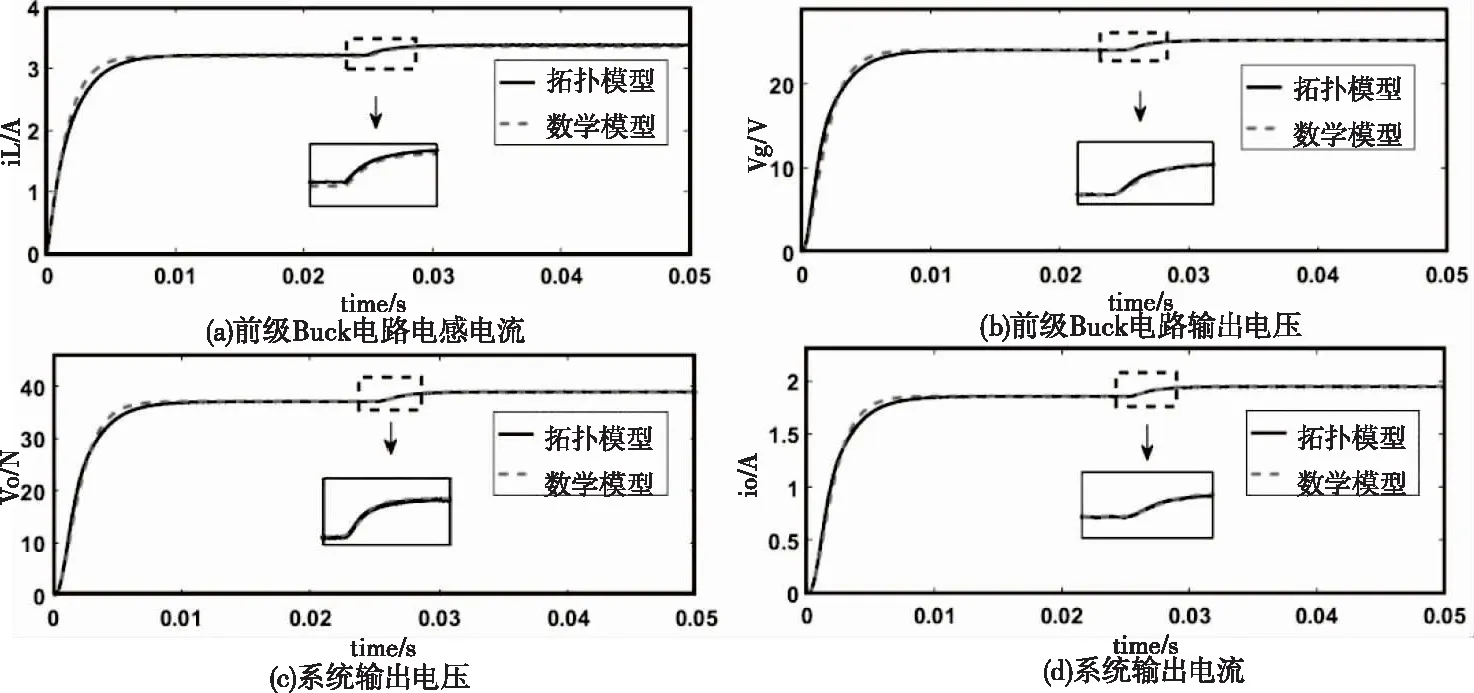
图5 控制信号及扰动作用下的直流变量波形对比图

从图5中可以看出，在阶跃信号作用下的动态过渡过程中，两种模型的响应存在相位与幅值上的微小差异，而在输入电压小信号扰动作用下两种模型的直流变量波形几乎完全一致。初始阶跃响应过程的差异一方面是由于在DC/DC单元建模时将其后级负载看作一个固定的等效电阻，然而实际上它是非线性负载；另一方面是由于DC/DC变换器的数学模型是小信号模型，且对MCR-WPT单元建模时将直流变量与交流变量分别用傅里叶级数的零阶分量和一阶分量进行了近似处理。

设系统各变量的初始条件为零，对模型(14)求解，根据式(11)得到状态变量的时域运行轨迹，同时基于Simulink拓扑模型进行仿真，得到两种模型下原边电容电压vcp的时域运动轨迹对比图，如图6所示。

从图6中可以看出，两种模型下原边电容电压vcp的时域运动轨迹几乎重合，在初始动态过渡过程中存在相位和幅值上的微小差异。在0.025秒时给输入电压加入扰动，vcp经过短暂的振荡过渡后进入稳态，并且在扰动过渡过程中及进入稳态后，两种模型下的电压波形都是吻合的。

图6 原边电容电压vcp时域运动轨迹对比图

由以上分析可以得出，对于带前级Buck控制的MCR无线充电系统所建立的数学模型与实际系统模型具有较高的吻合度。

3.3 系统稳定性的分析

基于已建立的数学模型对系统进行稳定性分析，将3.1节中的参数值代入式(15)绘制系统Bode图如图7所示。

图7 系统Bode图

原始系统为0型系统，其直流增益及低频增益约35.7dB 的水平线，系统以斜率-20dB/dec 穿越 0dB 线，相位交越频率为2.25kHz，增益裕量为16.4dB，剪切频率为778Hz，相位裕量位30.3°，系统是稳定的。

3. 4 控制特性分析

本系统通过对前级DC/DC变换器占空比的调节实现来终端负载功率的控制，下面根据所建立的数学模型对占空比-功率控制特性进行分析。

系统输出电压为直流变量，其幅值可以用〈vcf〉0表示，则系统的输出功率为

(16)

x=-A-1Bu

(17)

解得电感L的稳态电流为

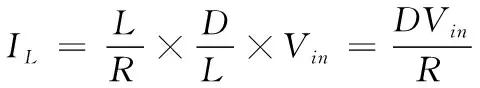
(18)

稳态输出电压为

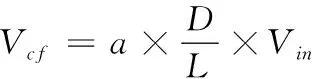
(19)

其中，a是一个与系统参数相关的值，则系统的稳态输出功率为

(20)

系统处于稳态时，输入电流Iin与电感L的电流

Iin=DIL

(21)

则系统的效率为

(22)

根据表1提供的数据，可以得到a=0.0232，由式(20)和式(22)得到不同占空比下输出功率、传输效率的特性曲线如图8所示。

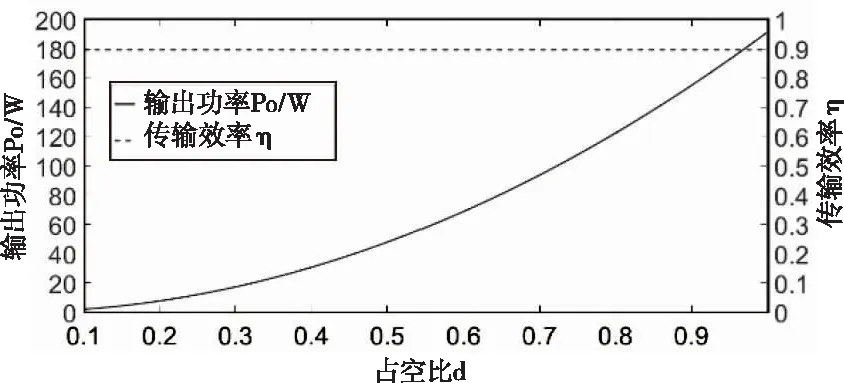
图8 输出功率和传输效率与占空比的关系曲线

从图8可以看出，通过调节DC/DC单元的占空比，能够很好地实现对输出功率的控制，并且在功率调整的同时系统的传输效率保持不变。

4 结论

本文采用SSA法和GSSA法对带前级DC/DC控制的MCR无线充电系统建立了其线性化数学模型，并基于Matlab软件对数学模型进行了验证，结果表明，所建模型与实际系统模型具有较高的吻合度。基于此模型，分析了系统稳定性及控制特性，分析结果表明，系统是稳定的，并且在不改变系统传输效率的前提下，前级DC/DC单元可以很好地实现对输出功率的控制。本文所建立的数学模型，可为系统的性能分析和控制器的设计提供可靠的依据。