用于仿真的非线性消谐电阻模型建立

董张卓，白翰林，李晓娟，宋 伟

(1. 西安石油大学电子工程学院，陕西 西安 710065；2.中煤西安设计工程有限责任公司，陕西 西安710054)

1 引言

中性点非有效接地配电网，扰动使分布式对地电容和电磁式互感器产生铁磁谐振[1]，这是配电网中常见的一种过电压异常运行状态。这种异常运行状态轻则造成停电、重则可能引起设备的损坏、引起重大事故。在电压互感器一次侧的中性点接入非线性消谐电阻器是一种得到广泛应用的消谐方式[1，2，3]，但安装非线性消谐电阻后，影响互感器的测量精度[4，5]。在对这种电磁谐振现象的仿真研究过程中，需要建立非线性电阻的仿真模型。消谐电阻所采用的非线性材料的微观特征[6]，即晶界、晶粒电阻率、以及晶粒间放电、容性效应等耦合决定决定其非线性电阻特性。

表示非线性电阻特性可用i=f(v)(简称v-i)曲线或v=f-1(i)(简称i-v)曲线，对于非线性电阻，v-i和i-v无本质区别，不失一般性，以下叙述再不需要区别v-i和i-v，统称i-v特性。为了表示消谐电阻的特性，提出一种用递推方式计算i-v曲线的方法。首先，采用和消谐电阻工作环境相一致的测试方式，得到消谐电阻加入由小到大工频正弦波电压后，测量得到其对应电压、电流有效值和功率。然后，采用递推算法计算i-v特性曲线。

假设i-v为分段线性曲线，各分段的电流和电压能用直线方程表示，在已知上一个分段末端电流值的情况下，即已知该分段前的i-v曲线情况下，通过建立的功率计算方程，求解方程能得到当前分段的末端电流值。从第一个测量点开始计算，通过递推依次得到每一个分段末端电流，最终得到非线性电阻的分段线性化i-v特性曲线。

得到离散化的i-v特性曲线数据后，通过曲线拟合得到消谐电阻的i-v解析式。

2 消谐电阻i-v特性

消谐电阻的i-v特性为非线性曲线，图1给出了一个周期正弦波加在消谐电阻上的电压、电流随时间变化以及i-v特性曲线。消谐电阻所加的正弦电压如图1(a)；消谐电阻的i-v曲线，如图1(b)所示；产生的消谐电阻电流曲线，如图1(c)所示。

从图1(a)(c)曲线可以看出，电压、电流随时间变化函数，以及i-v均为奇函数，因此，计算i-v时，可以仅计算得到其处于第一象限部分。

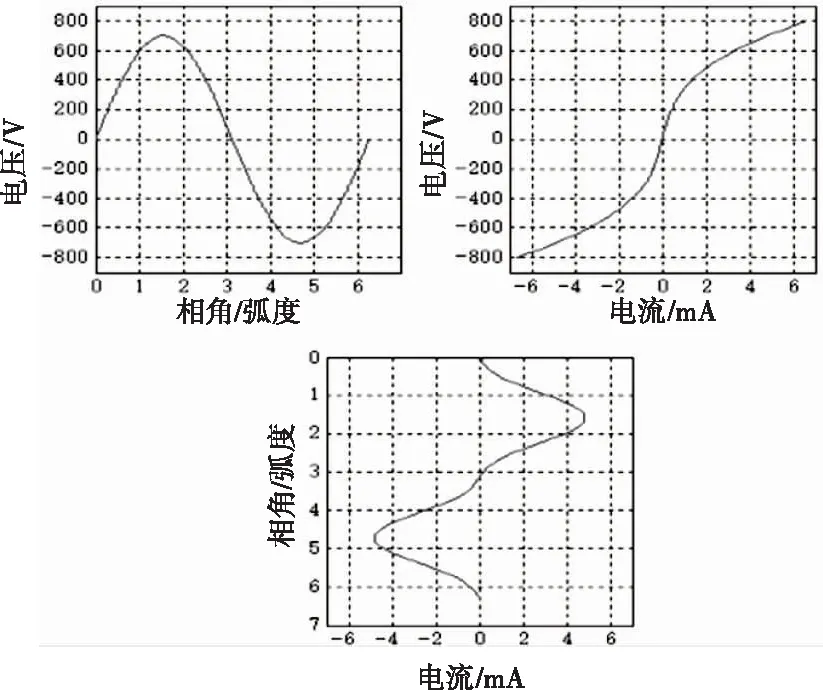
图1 消谐电阻的i-v特性和电压电流关系

消谐电阻的i-v特性用分段直线段来近似。图2给出了在消谐电阻加入1/4周期正弦波电压时，三条曲线上各个点之间的关系。图2(a)(c)曲线的相角，为用弧度表示的时间轴，其值为ωt，ω为正弦波的角频率，t为时间。在给定相角ωti情况下，通过电压曲线做水平线和电流曲线做垂直线，即可确定i-v曲线上的点。

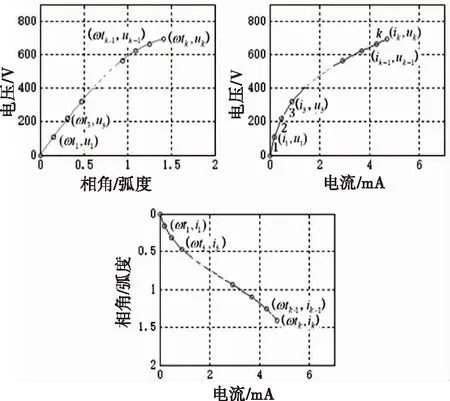
图2 1/4周期消谐电阻i-v曲线和电压、电流曲线上点的关系

3 消谐电阻i-v特性的基础数据

给非线性消谐电阻R上加入正弦电压

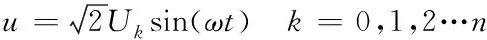
(1)

式(1)中：Uk为所加正弦电压有效值；ω为所加电压的角频率。k=0，对应于原点，即电压U0=0。

通过给非线性消谐电阻加入从小到大的n个电压uk，可以得到电流Ik、以及功率Pk的值。最终形成一组Uk，Ik，Pk，k=0，1，2，…，n。

4 i-v特性递推计算原理

i-v特性曲线上各点的电压值即为测试得到的电压有效值的峰值

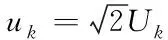
(2)

用分段线性化的方法列出计算Pk的方程，通过求解方程得到流过非线性电阻的电流峰值ik。若已算出i1，i2，…，ik-1，计算ik的值，则将i-v特性曲线上从原点到(uk，ik)点共k个线性，用分段直线方程式表示，其中第j段，j=1，2，…，k，由两点(ij-1，uj-1)，(ij，uj)决定的直线方程为

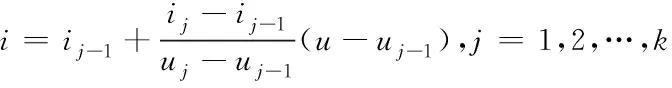
(3)

根据有功功率定义及电压电流的对称性

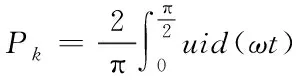
(4)

将 (1)(3)式代入(4)式得

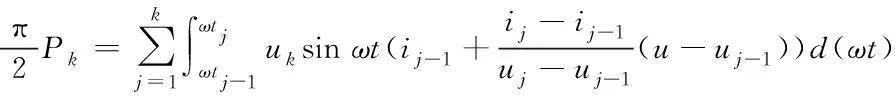
(5)

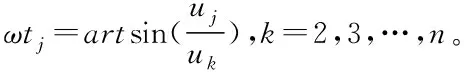
5 消谐电阻基础数据获取

在消谐电阻两端加入工频正弦电压，测量得到电流有效值和电阻消耗的功率。电路如图3所示。

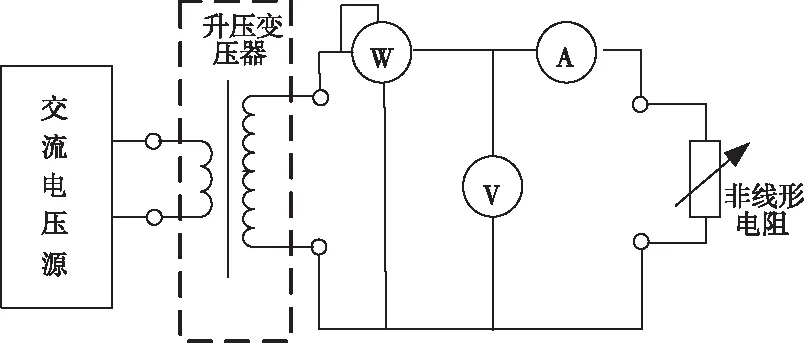
图3 非线形电阻特性测试原理图

测试时，通过升压变压器调节非线性电阻两端的电压，在特定电压点，记录电流值和功率值。

在实验室对一个RXQIII-10(D)消谐电阻进行测试。所加电压为标准的正弦波形，正弦波形由标准正弦波电源产生，功率、电压用日置PW3335测试。调节电压，测试得到电压、正弦电流值，正弦电压值范围为0～876V。测试得到的消谐电阻电压、电流、功率数据如表1所示。测试时消谐电阻典型的电压、电流波形如图4所示。

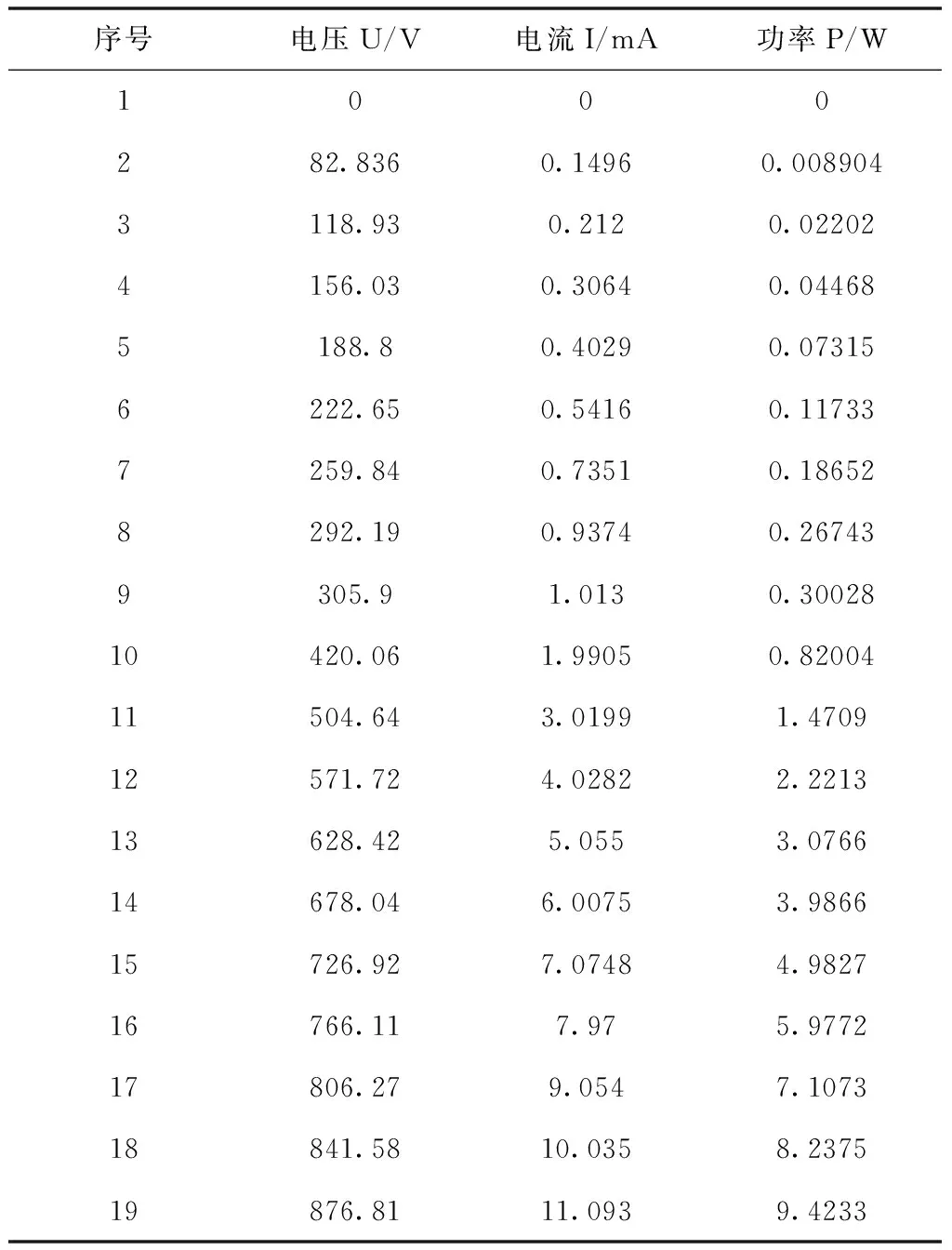
表1 消谐电阻测试数据

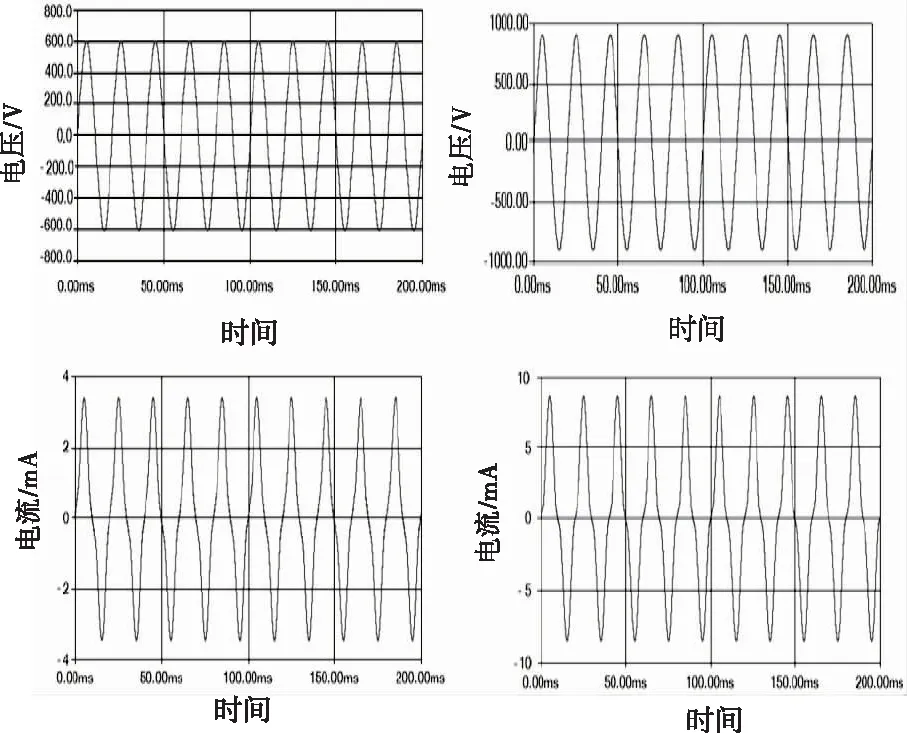
图4 消谐电阻典型电压电流波形

从图4所示的消谐电阻电压、电流随时间变化的曲线可以看出，在电压为正弦波情况下，消谐电阻的电流波形为尖顶似正弦波，这种电流波形中3次谐波占有主导地位。图5给出了当非线性电阻加载正弦电压时，其电流有效值、功率、以及非线性静态电阻和电压有效值，以及静态电阻和电流有效值的关系。

图5(a)为消谐电阻加正弦电压时，对应的非正弦电流有效值曲线。随着电压的加大，电流有效值呈现非线性变化，变化过程为单调增加，曲线斜率由小逐渐变大。图5(b)为消谐电阻功率随外加正弦电压有效值的变化曲线，和电流有效值随电压变化的情况类似，功率和电压有效值为非线性关系，且电压较低时，功率变化较小，随电压增大，功率变化随之增加，表明随电压变化，消谐电阻变小。消谐电阻功率在0～10W之间。在电压较小时，消耗功率小于平均值。

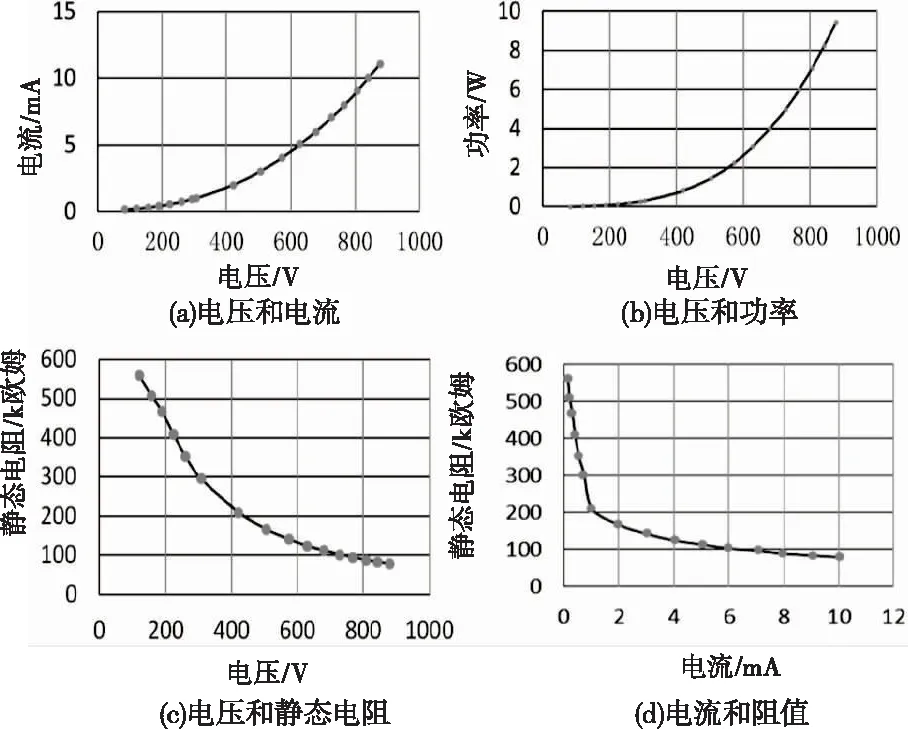
图5 消谐电阻电气参数特性曲线

图5(c)为非线性电阻阻值随电压的变化情况，随电压的增大，静态电阻在变小，电阻由550kΩ，逐渐变化到80kΩ。图5(d)给出了消谐电阻的阻值，随电流的变化规律，随电流增大，电阻值非线性减小。

6 消谐电阻的i-v特性

按照2节的计算方法，设计了如图6所示的程序流程，根据流程编制了消谐电阻i-v计算程序。计算得到的RXQIII-10(D)i-v数据如表2。根据表2绘制的i-v曲线如图7所示。

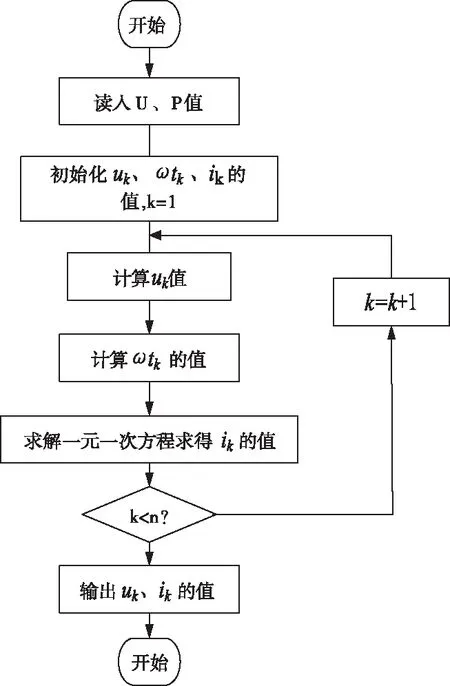
图6 程序流程图

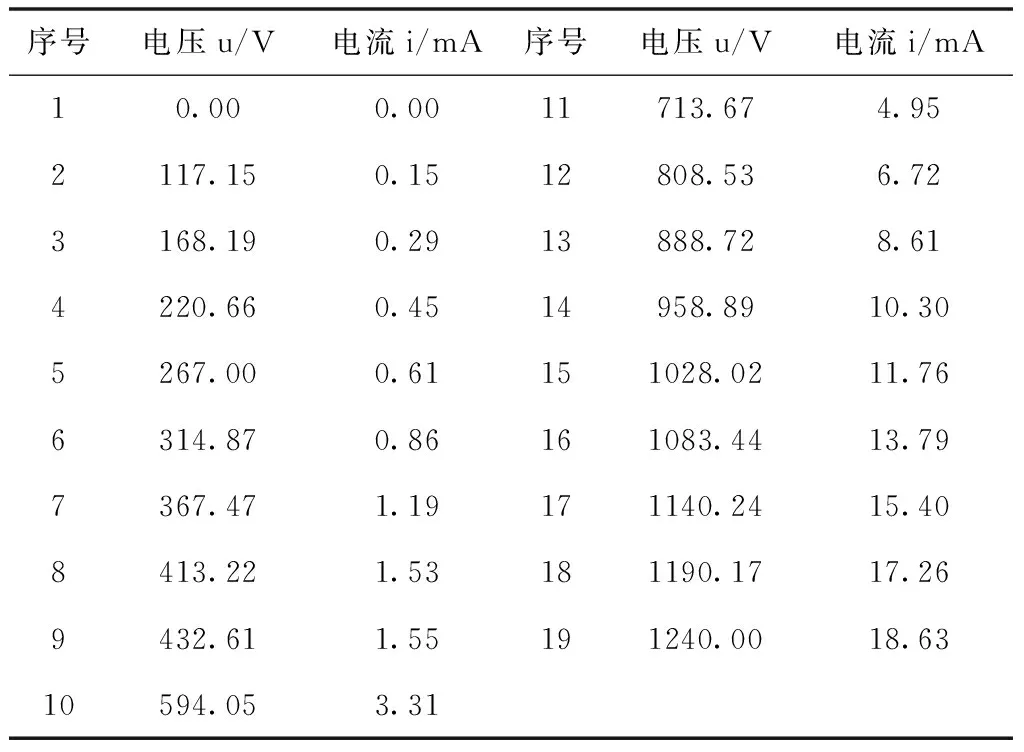
表2 RXQIII-10(D) i-v数据表

图7为消谐电阻的i-v特性曲线，从图7的消谐电阻i-v曲线可以看出，其为单调下凹曲线，随电流的增大，电压同时增大，曲线的斜率随电流的增大逐渐减小。

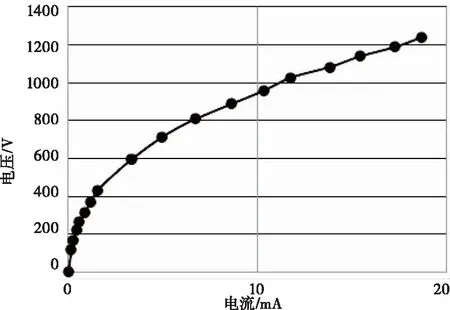
图7 消谐电阻i-v曲线

图8给出了消谐电阻的静态电阻特性，其值从80kΩ～800kΩ范围变化。

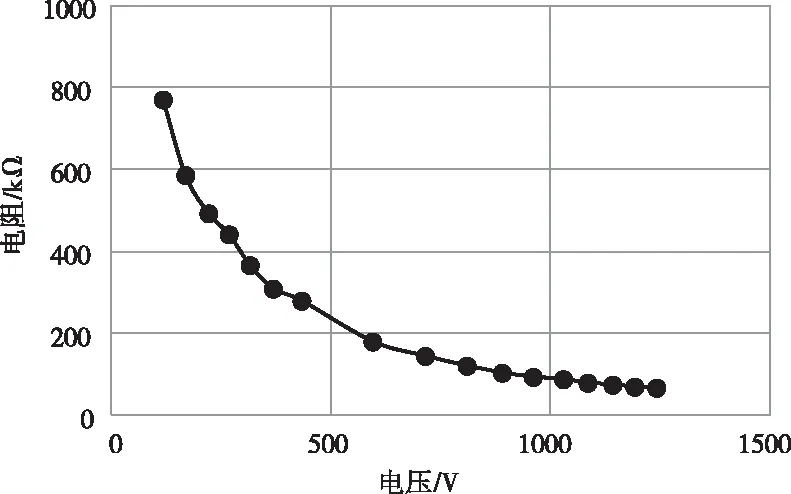
图8 消谐电阻器的静态电阻特性

7 消谐电阻仿真模型

建立非线性消谐电阻的仿真模型的关键点为非线性消谐电阻的伏-安特性函数的建立。得到i-v函数后，能方便地在Simulink中搭建仿真模型。仿真模型搭建分为数据预处理、仿真拟合、模型建立三部分。

7.1 数据预处理

由于非线性消谐电阻i-v特性为奇函数，并且i-v特性函数为经过坐标的原点的连续函数，为了避免函数在经过坐标原点的不连续性，在拟合前需要对(u，i)序列数据进行扩展，取负的方式得到奇函数的另外一半数据(-u，-i)在此基础上对数据集合按电压值进行扩展并平移处理。

1)将处于第一象限的(i，u)数据集合，按照(6)式扩展出位于第三象限的数据集合。

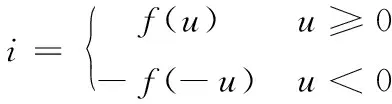
(6)

2)将u值进行平移处理，定义u′=u+umax，得到(u′，i)数据集合，其中，umax为u的最大值。

7.2 i-v的拟合

采用Simulink中的函数拟合工具，可以方便拟合出i-v函数。

7.3 仿真模型的建立

非线性消谐电阻i-v特性为v=R(i)i，电阻值为i的函数。当已知电阻R的i-v特性，通过电压v可以计算得到电流i，或反之，通过电流i可以计算得到电压v。如图9所示，在Simulink中，以电流i作为输入参数，用信号控制电流源方式来建立其仿真模型。

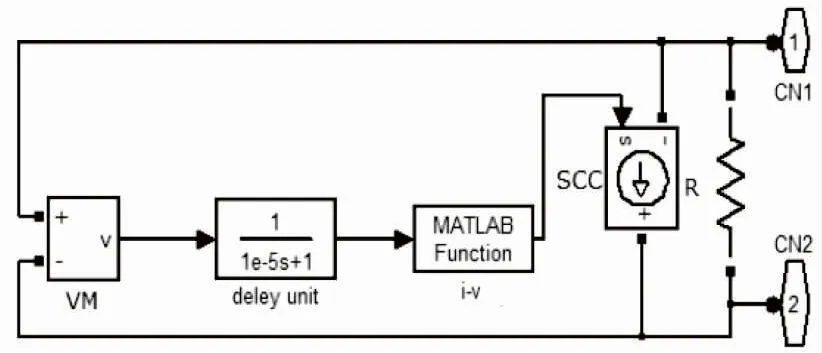
图9 非线性电阻仿真模型

8 模型验证

在Simulink7.6环境下，建立消谐电阻的仿真模型，给消谐电阻模型加载各种幅度正弦波电压，得到电流i波形。仿真波形和实际测试电压、电流波形进行对比，两者一致。

图10给出了消谐电阻输出的外加正弦电压有效值为600V时的电流波形图。

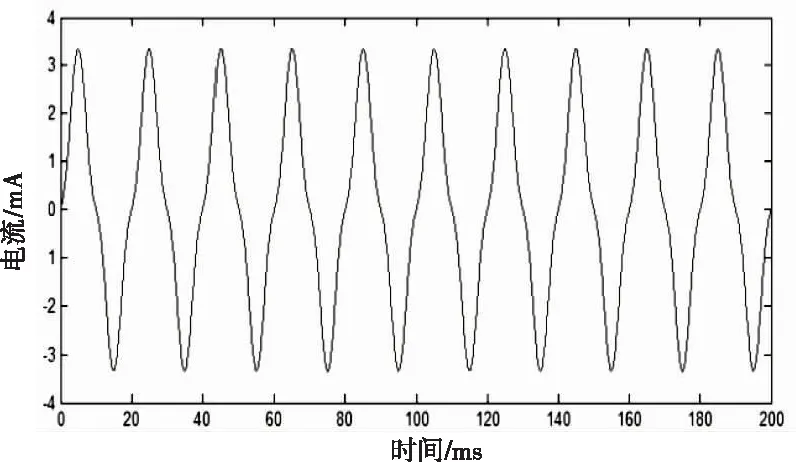
图10 外加600V正弦电压时消谐电阻电流仿真曲线

9 结论

提出的一种建立仿真用消谐电阻模型方法。首先依据测量的一组电压电流有效值、以及功率序列值，通过递推的方法得到消谐电阻i-v特性。然后通过对i-v平移方法，得到数据，以此数据进行拟合得到拟合的i-v函数。根据i-v函数建立消谐电阻的Simulink仿真模型。

1)消谐电阻i-v递推方法，能得到准确的i-v特性。

2)通过数据扩展、平移方法建立的仿真模型，能有效避免过零点不连续问题。