基于改进滑模算法的无人机抗风雨研究
袁建华,刘 宇,赵子玮,何宝林
(三峡大学,湖北 宜昌443000)
1 引言
四旋翼无人机是一种小型无人机,具有欠驱动、非线性、强耦合等特性,加之运行高度较低,易受风雨干扰,目前针对无人机抗风性模型研究很多,国内外也提出多种控制方法方案,如PID控制、反步控制、自适应控制、鲁棒控制、神经网络控制和滑模控制等。当前没有一种考虑在复杂风雨环境下的无人机模型,建立一种风雨干扰下无人机数学模型和构造可以抗风雨干扰的控制器以实现无人机可以在复杂条件下工作是目前的主要任务。
文献[1,2]提出了解耦PID四通道控制器,在未计算外部环境因素的干扰下能够完成自稳定控制,但其与无人机实际飞行环境不符;文献[3]使用的是反步法的控制方式,但要使系统稳定需设计很复杂的反馈过程才行;文献[4]采用改进饱和函数的传统滑模控制,取得了鲁棒性强、响应速度快的闭环控制系统,但饱和函数的参数选择较多,实现起来较复杂,在模拟风场扰动时将扰动作用在电机模块上难免会与实际情况存在一定误差。文献[5]采用一种终端滑模控制器,具有快速响应和消除抖振的优点,但只考虑了风场干扰,未考虑风雨情况下无人机的飞行。
本文研究内容和目的如下,建立一种风雨干扰下的无人机模型,采用新型反正切饱和函数的滑模控制算法计算各个控制律,减小滑模控制中存在的抖振问题,建立稳定的抗风雨干扰的控制器。
2 四旋翼无人机传统动力学模型
1)坐标系建立及坐标系变换
将x轴设为无人机的飞行方向,取无人机绕x轴,y轴,z轴旋转分别为横滚角,俯仰角,偏航角,表示为α,β,γ。
经过对无人机的转速的控制完成对无人机的横滚,俯仰,偏航姿态的控制[6]。建立如图1所示的地面坐标系OEXEYEZE与机身坐标系OBXBYBZB。
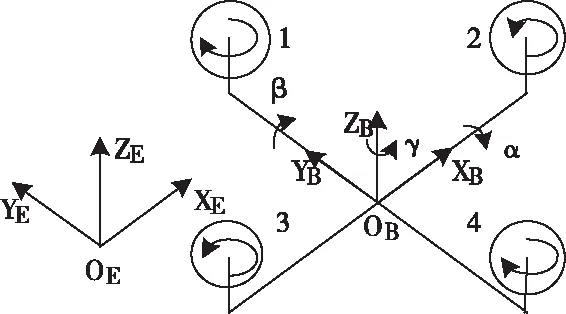
图1 地面坐标系与机体坐标系示意图
根据欧拉角定义,无人机的机体坐标系以ZB轴,YB轴,XB,轴顺序旋转可变换成地面坐标系,由机体坐标系到地面坐标系的转换矩阵为

(1)
式中;α横滚角,β俯仰角,γ偏航角
2)旋翼动力模型
四旋翼无人机升力与旋翼转速的平方是正比关系[7],旋翼的转速为ni,(i取1,2,3,4),则

(2)
式中;λ为旋翼升力系数,ni各旋翼的转速。
四旋翼无人机通过改变各个电机的转速差实现横滚、俯仰和偏航动作,建模时,将四旋翼无人机模型分解成四个独立通道U1U4,分别控制垂直升降、翻滚、俯仰和偏航,可得动力学公式
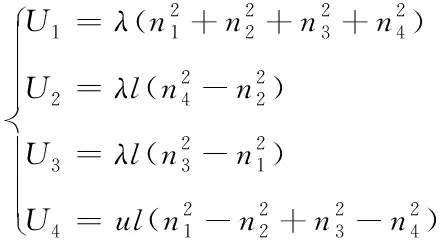
(3)
式中;l是质心到旋翼的距离;u阻力系数。
3 无人机风雨综合受力分析及模型建立
3.1 风场下四旋翼无人机受力分析及模型建立
四旋翼无人机在有风的环境中飞行时,易受其干扰,考虑到无人机和旋翼面积较小,只计算旋翼受风场干扰的影响。无人机旋翼转动时,旋翼上下面空气压强不同形成压强差为无人机提供升力[5],如图2所示.
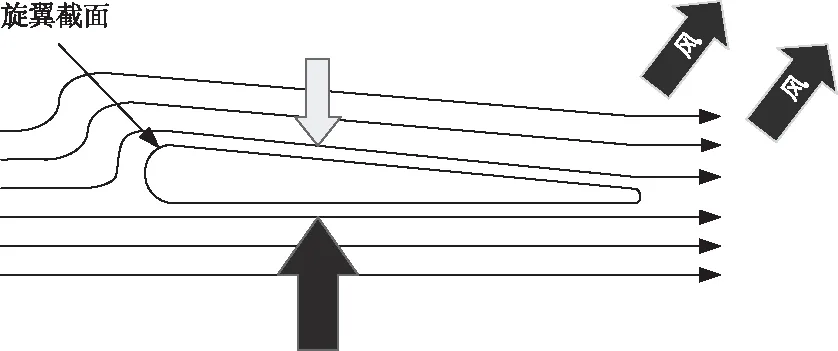
图2 风场下旋翼的来流示意图
旋翼在风场环境中,风场会影响其上下空气流速形成压强差,其产生的力的方向和升力相同,风场力公式为
Fwi=2ρAVdiVw
(4)

(5)
式中;ρ空气密度;A旋翼扫过的面积;Vw旋翼的诱导速度;Vdi风速;Fi旋翼的升力。
通过Dryden模型对紊流风场进行描述,Gauss白噪声信号通过成形滤波器转化为大气紊流信号,形成对紊流风场模型的仿真模拟,风场干扰模型如下图3所示。

图3 风场干扰模型
简化的成形滤波器的传递函数为
Gx(s)=Kx/(Txs+1)
Gy(s)=Ky/(Tys+1)
(6)
Gz(s)=Kz/(Tzs+1)


(7)
3.2 雨场下四旋翼无人机受力分析及模型建立
1)降水粒子的谱分布
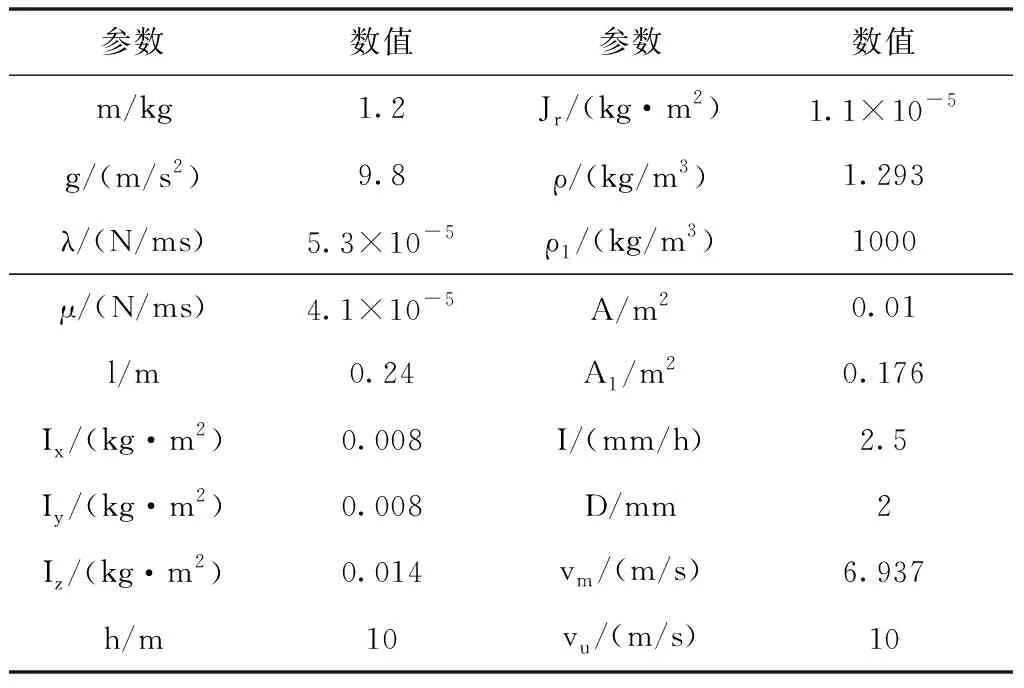
降雨时雨滴在空气中的大小,一般使用直径D0来表示。其形状在140μm 通过研究文献数据发现,雨滴谱一般服从负指数分布,最常用的是Marshall-Palmerspectrum,简称M-P 谱[8],即 n(D)=n0e-ΛD (8) 式中:n0=8×103;Λ为斜率因子,Λ=4.1I-0.21,I是雨强(mm/h);D为直径(mm)。 2)雨滴降落的末速度 雨滴从空中降落时会受到重力和空气阻力的影响,开始重力大于空气阻力,雨滴加速运动,当速度到达一定时,重力与空气阻力相等,雨滴匀速运动,此刻速度为其终末速度Vm。研究相关文献发现了不同的雨滴降落速度公式,经过比较发现文献[9]提出的公式与实测资料相近。 (9) 1.0mm (10) (11) 3)雨滴冲击力的计算 无人机在空中飞行时无人机表面会受到降雨的冲击,雨滴在撞击无人机表面时,速度在极短时间内降为零,符合动量定理[10]。设雨滴质量m,终末速度Vm,撞击时间τ,雨滴撞击无人机表面受力如图4所示。 图4 雨滴撞击时无人机受力图 由动量定理知 (12) 式中:f(t)为单个雨滴撞击力矢量;v速度矢量。 雨滴在时间τ内对无人机的撞击力F(τ)为 (13) 假设雨滴下落时为一球体,m=πρ-1d3/6,τ=d/2v则 (14) 在考虑雨滴对无人机表面的冲击力时,将单个雨滴的冲击力转化为均布面荷载(N/m2)作用在结构上 Fd=αF(τ)/(A) (15) 式中;F(τ)为单个雨滴撞击力;A为作用面积,A=πd2/4 ;τ作用时间;α为雨滴在空气中的占有率,α=πd3n(D)/6 。 将式(14)代入式(15),可得单位体积内某直径大量雨滴的冲击力 (16) 则无人机表面受力为 (17) 式中;A1为无人机表面积。 无人机在空中飞行时无人机表面受到降雨的冲击,其冲击力可分解为x轴,y轴z轴三个方向,x轴,y轴雨滴速度V可取顺风向水平风速Vx,Vy,z轴方向V取雨滴终末速度Vm,计算出无人机受力Fd如图5雨场干扰模型所示。 图5 雨场干扰模型 四旋翼无人机是一种六自由度、四输入的非线性、欠驱动的系统,具有较强的耦合性[11]。分析旋翼在风场作用下的受力分析和机身在雨场作用下的受力分析,建立无人机在风雨场扰动下的动力学模型。 (18) 式中;F为合外力,T为合外力矩,m为质量,E为三阶单位矩阵,I为转动惯量矩阵,无人机的加速度,为机轴的欧拉角加速度。 (19) 四旋翼无人机在空中飞行时,对其进行飞行受力分析。其在风雨环境下飞行时受到的合外力为无人机自身的升力和重力和外部的风雨合力,合外力矩为无人机的姿态运动产生的气动力矩,旋翼的陀螺力矩,和风雨作用产生的风雨力矩。四旋翼无人机在风雨环境下的动力学模型为 (20) (21) (22) 式中;nr=-n1+n2-n3+n4;Jr转动惯量。 四旋翼无人机控制是一种的欠驱动、非线性的系统[13-15]。针对无人机在风雨干扰情况下的飞行控制,选用一种滑模控制算法。该控制方法具有以下优点: 1) 滑模控制拥有对外界干扰不灵敏,不受外界干扰影响的特性,并且适用于非线性系统;2)可保证在有限时间内迅速到达滑模切换面,且收敛时间可进行调整; 3) 选用新型反正切饱和函数的趋近律,消除了传统饱和函数参数选择较多,实现起来较复杂的问题。 根据建立的无人机动力学模型建立一种抗风雨干扰的控制器,使无人机能够在风雨的环境中安全的飞行。通过无人机动力学公式控制器的输入控制量为U=(U1U2U3U4)T。无人机控制系统如图6所示。 图6 无人机控制系统图 s=-εsgn(s)-ks是一种传统滑模控制趋近律,其因为sgn符号函数的特性存在抖振问题,以具有平滑和有界特性的反正切函数代替开关函数可以有效减少抖振问题。 sat(s)=arctan(c0·s) (23) 式中;c0>0,且为常数。 四旋翼无人机为二阶非线性系统,对无人机的控制可分为高度控制和姿态控制。其中高度控制器的建立,设预期和实际误差为ez=zd-z,趋近律为sz=-εarctan(sz)-ksz依据高度动态方程,得出状态空间方程为下 (24) 则滑模切面为 (25) 设计滑模控制律为 (26) 式中;δ,ε,k皆大于0。 利用Lyapunov定律验证控制器的稳定性,选取Lyapunov函数 (27) =Sz·(-εarctan(sz)-ksz)<0 (28) 经过上式可得高度滑模控制器稳定。 其中姿态角以横滚角α为例,建立姿态控制器,定义eα=αd-α,趋近律为sα=-εarctan(sα)-ksα依据姿态方程得出状态方程为下 (29) 则滑模切面为 (30) 设计滑模控制律为 (31) 同理用Lyapunov定律验证姿态控制器的稳定性, (32) (33) =Sα·(-εarctan(sα)-ksα)<0 经过上式可得姿态滑模控制器稳定。 同上可得姿态角控制律 (34) (35) 使用建立的滑模控制律构造无人机控制系统中的控制器,使用建立的无人机数学模型构建无人机模块,构建的风干扰模块如上图3所示,构建的雨干扰模块如上图5所示。建立无人机在风雨干扰下的模型如图7所示。 模型中各参数设置如下表1。 表1 无人机模型参数 图7 系统仿真模型结构图 滑模控制器的参数分别设定为c0=5,δ=3,ε=4,k=3。起始高度z=0,期望高度zd=10。起始姿态为(α,β,γ)=(-π/4,-π/3,-π/2);期望姿态为(αd,βd,γd)=(0,0,0)。根据控制器仿真参数及上表无人机模型数据的设置,取仿真时间为10s,通过仿真得到如图8风场干扰仿真图,图9雨场干扰仿真图和图10无人机飞行姿态仿真图。 图8 风场干扰仿真图 图9 雨场干扰仿真图 图10 无人机飞行仿真图 由图8,图9可知无人机在空中飞行在10m时受到风雨干扰的波形,由图10可知无人机在风雨干扰下仍然能够在2s内稳定并由起始高度0m飞行到10m,由起始姿态角(-π/4,-π/3,-π/2)稳定到期望姿态(0,0,0)。 本文研究了四旋翼无人机在风雨环境下无人机受力情况和建立一种考虑风雨干扰的无人机动力模型,采用新型反正切饱和函数的滑模控制算法,建立一种抗风雨干扰的控制器。通过MATLAB仿真表明,建立了符合实际情况的风雨干扰无人机动力模型,设计的采用新型反正切饱和函数控制器具有稳定性好,收敛速度较快,和鲁棒性较强的特点。 本文研究的无人机动力模型能有效的表现出无人机在外部复杂环境干扰的情况下的飞行情况。



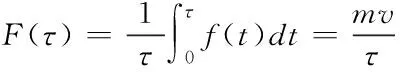



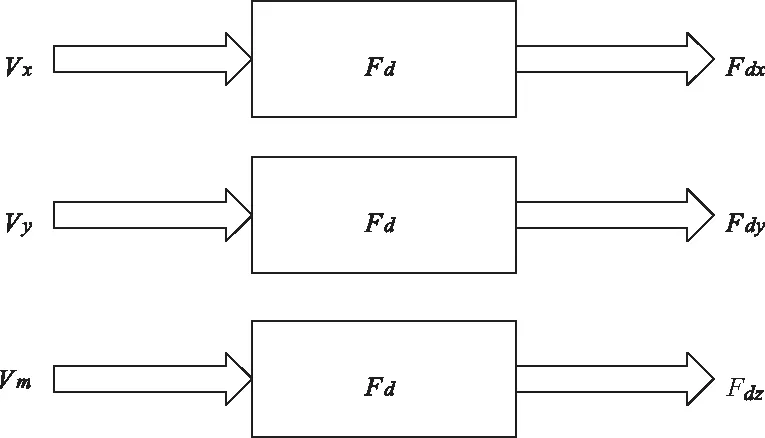
3.3 无人机综合受力分析及动力模型建立
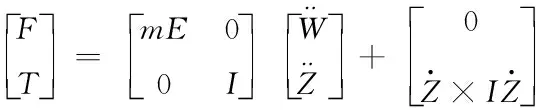




4 一种抗风雨干扰的滑模控制器建立

4.1 选用新型反正切饱和函数
4.2 滑模切换面设计





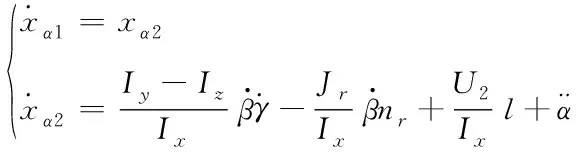






5 系统仿真与分析
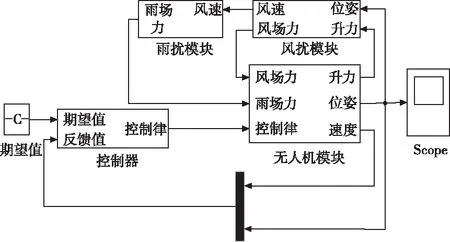

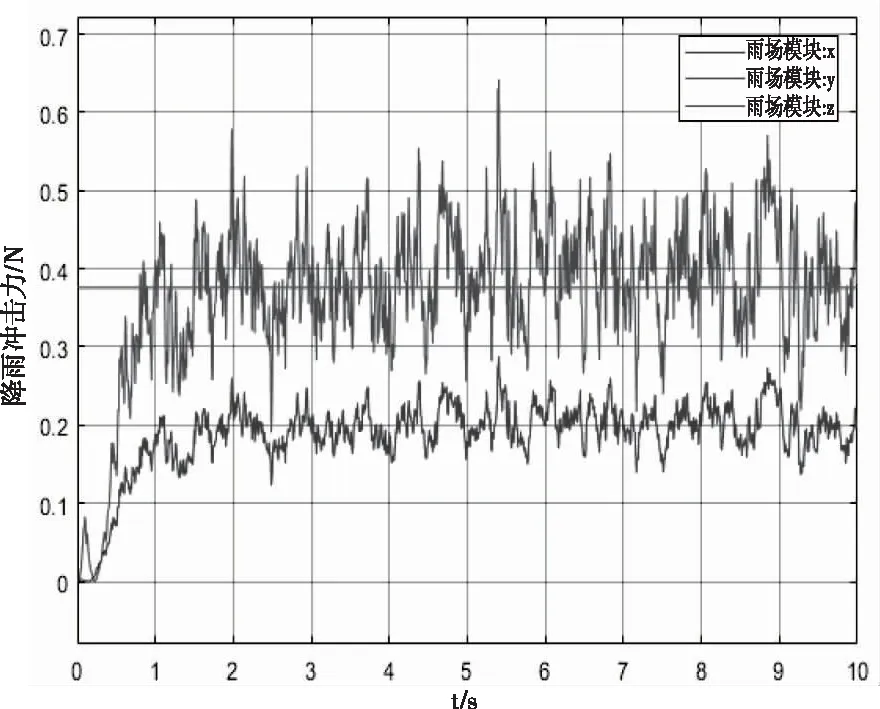

6 结论

