一道不等式证明的探究
⦿福建省莆田第六中学 李德琳
我们熟知的重要不等式结论“ex≥x+1,当且仅当x=0时等号成立”“lnx≤x-1,当且仅当x=1时等号成立”,经常巧妙设置于题中,是破解一些与不等式有关的问题比较常用的重要结论.创设数列不等式的证明问题,是高考数学中比较常见的一类综合交汇题,合理融合函数与方程、导数、数列、不等式及其证明等众多知识,实现命题的综合性、交汇性与创新性,倍受各方关注.
1 问题呈现
问题[陕西省咸阳市2022年高考模拟检测(二)数学(理科)试题·21]已知函数f(x)=lnx-kx+1.
(1)若f(x)≤0恒成立,求实数k的取值范围;
此题以含参函数所对应的不等式恒成立来巧妙创设情境,进而确定对应参数的取值范围,在此基础上构建重要不等式结论“lnx≤x-1,当且仅当x=1时等号成立”,进而通过合理代换,结合放缩处理与变形,巧妙证明对应的数列不等式.
2 问题破解
方法1:分类讨论法+裂项法1.

当k≤0时,f′(x)>0恒成立,则函数f(x)在(0,+∞)上单调递增.
因为f(1)=-k+1>0,所以f(x)≤0不恒成立.
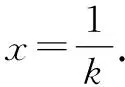

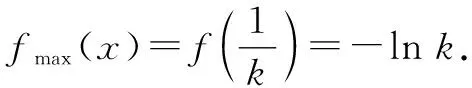

所以实数k的取值范围是[1,+∞).
(2)证明:由(1)知,当k=1时,有不等式lnx≤x-1对任意x∈(0,+∞)恒成立,当且仅当x=1时等号成立.
所以x∈(1,+∞),lnx 当n≥3时, 解后反思:解决与含参函数有关的不等式问题,可以借助参数的不同取值情况加以分类讨论;而证明不等式时,利用(1)中重要不等式结论加以转化,通过合理放缩,借助裂项求和来转化,实现对应不等式的证明与应用. 方法2:分离参数法+裂项法2. 若x∈(0,1),则g′(x)>0,函数g(x)单调递增;若x∈(1,+∞),则g′(x)<0,函数g(x)单调递减. 于是gmax(x)=g(1)=1. 结合f(x)≤0恒成立,可得k≥1. 所以实数k的取值范围是[1,+∞). (2)证明:由(1)知,当k=1时,有不等式lnx≤x-1对任意x∈(0,+∞)恒成立,当且仅当x=1时等号成立. 所以x∈(1,+∞),lnx 解后反思:解决与含参函数有关的不等式问题,通过分离参数,借助构建函数,通过确定函数的最值得以解决参数的取值范围问题,也是解决此类问题比较常见的一种技巧方法;不等式证明中的不同放缩尺度以及对应的裂项求和处理,都是解决问题的重点,关键是合理配凑与巧妙转化. 保持创新问题背景,借助不同数列不等式的给出,通过不同类型的参数代换处理,实现不同数列不等式的证明问题,拓展思维,倡导应用. 变式1已知函数f(x)=lnx-kx+1. (1)若f(x)≤0恒成立,求实数k的取值范围; 解析:(1)同原问题中的解析(1),可得k≥1,所以实数k的取值范围是[1,+∞). (2)证明:由(1)知,当k=1时,有不等式lnx≤x-1对任意x∈(0,+∞)恒成立,当且仅当x=1时等号成立. 所以x∈(1,+∞),lnx 令x=n2(n∈N*,n>1),代入lnx 变式2已知函数f(x)=lnx-kx+1. (1)若f(x)≤0恒成立,求实数k的取值范围; 解析:(1)同原问题中的解析(1),可得k≥1,所以实数k的取值范围是[1,+∞). (2)证明:由(1)知,当k=1时,有不等式lnx≤x-1对任意x∈(0,+∞)恒成立,当且仅当x=1时等号成立. 所以x∈(1,+∞),lnx 不妨令 变式3已知函数f(x)=lnx-kx+1. (1)若f(x)≤0恒成立,求实数k的取值范围; 解析:(1)同原问题中的解析(1),可得k≥1,所以实数k的取值范围是[1,+∞). (2)证明:由(1)知,当k=1时,有不等式lnx≤x-1对任意x∈(0,+∞)恒成立,当且仅当x=1时等号成立. 所以x∈(1,+∞),lnx ③ 另一方面,令x=n2(n∈N*,n>1),代入不等式lnx ④ 解后反思:根据重要不等式结论“lnx≤x-1,当且仅当x=1时等号成立”的分析与求解,再结合所要证明的数列不等式的形式,抓住数列中相关项的结构特征,合理引入参数进行代换处理,结合不等式的性质以及所要证明的不等式结构的特征,巧妙放缩与转化,从而实现数列不等式的证明与应用. (1)记忆二级结论,掌握基本方法. 重要不等式结论“ex≥x+1,当且仅当x=0时等号成立”或“lnx≤x-1,当且仅当x=1时等号成立”,是导数及其应用中比较常见的二级结论,特别在一些小题(选择题或填空题)中,结合指数式或对数式的特征结构,利用相应的二级结论合理放缩,巧妙化归转化,使问题的求解更加直接、便捷,是破解一些与不等式有关的问题比较常用的重要结论与技巧策略. (2)巧妙参数代换,合理放缩处理. 涉及此类数列不等式的证明与应用,其实质就是巧妙利用重要不等式结论“ex≥x+1,当且仅当x=0时等号成立”或“lnx≤x-1,当且仅当x=1时等号成立”,借助结论实质结合数列不等式中相关的项加以合理参数代换,对比所证明不等式的结构特征与结论,合理放缩处理,巧妙变形转化,从而实现不等式的证明.
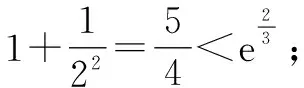



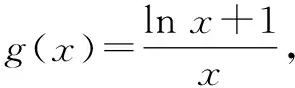




3 变式拓展

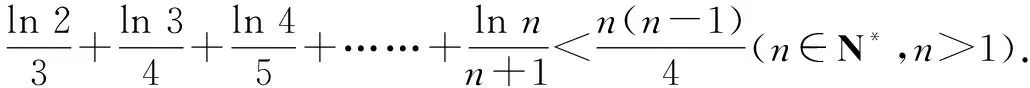






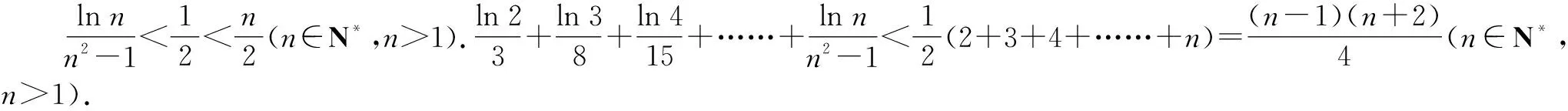
4 教学启示

