借助整体思想 打破常规思维

西华师范大学 林 芹 陈豫眉

1 引言

整体思想作为数学解题中的一个重要思想，旨在从已有问题的整体性质出发，认真观察问题的整体结构，并对其进行恰当地分析与改造，把握住问题的整体结构特征，运用“集成”的眼光，将其中的某部分看成一个整体，挖掘式子或图形间的内在联系，再对它们进行有目的、有意识地整体处理[1]，使原有式子或图形的结构更加清晰明了，容易解决.而这种以整体的眼光看待问题、解决问题的方法，贯穿于初中数学解题的多个方面.因此，笔者将结合实例围绕解题过程中蕴含的整体思想，挖掘其内含的解题策略，以期帮助学生了解更多的解题方法，培养学生的整体意识，提升学生的数学思维的敏捷性、概括性与灵活性.

2 整体思想在方程与不等式中的应用

2.1 在解方程(组)中的应用

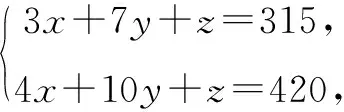
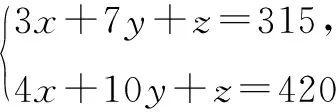
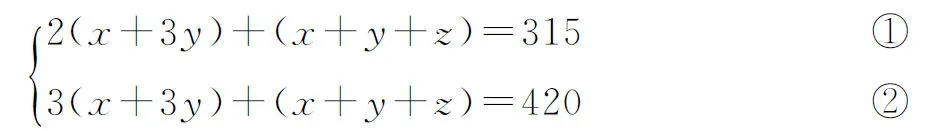
接着，运用整体思想将含有多个未知数的x+3y和x+y+z分别看成一个整体，再利用常规解法求得x+y+z的值.

从上述解方程(组)问题中不难发现，整体的实质就是一个转化过程，旨在将陌生的数学问题转化为熟悉的数学问题，将复杂的数学问题转化为简单的数学问题，使问题更加容易解决.而在解决方程或方程组的问题的过程中，利用整体思想将分式方程转化为整式方程，将高次方程转化为低次方程.不仅能够减少计算量，提升解题效率，还能够培养数学创新思维和整体意识.

2.2 在不等式(组)中的应用

例2已知1≤x-y≤2，2≤x+y≤4，求4x-2y的取值范围.

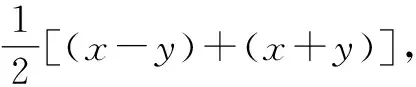
从上述不等式(组)问题中可以发现，不等式的学习是指从学生已有的等式、方程(组)中的“相等”关系到“不等”关系的过渡，是等式的延伸.因此，在求解不等式和不等式组时，我们也要大胆尝试解方程(组)时所采用的整体思想，着眼全局，把握已知与所求问题间的关联，找到快速解决问题的突破口.

3 整体思想在数与式中的应用

例3已知x2-3x-6=0，求2x2-6x+1的值.

分析:本题若用常规思路解决问题，我们需要先根据x2-3x-6=0求出具体x的值，再将x的值代入到方程2x2-6x+1中求解.但是，经观察求值式子可以发现x2-3x-6=0无法轻易因式分解，那么求未知数x的值就有一定的计算难度，需要借助一元二次方程的求根公式.很显然解题的过程变得较为繁琐，伴随着求根公式的引入，计算的难度有所增加，错误率也易增加.然而如果从式子的整体入手，认真观察式子的整体结构特征，就能够发现x2-3x恰好是2x2-6x的一半，即2x2-6x+1=2(x2-3x)+1，那么，可由x2-3x-6=0 变形得x2-3x=6，再将其整体代入到式子2(x2-3x)+1中，问题就迎刃而解了.

从上述代数式求值问题中，不难发现某些代数求值问题若拘泥于常规解法，则很难得到突破，易形成举步维艰的局势[2].但整体思想的运用，使我们快速且准确地找寻到问题突破的关键，让问题的解决变得更加简单明了.

4 整体思想在几何与图形中的应用

例4如图1所示，五边形ABCDE中，AB∥CD，∠HAB，∠GEA，∠EDF分别是∠BAE，∠AED，∠EDC的邻补角，求∠HAB+∠GEA+∠EDF的值.

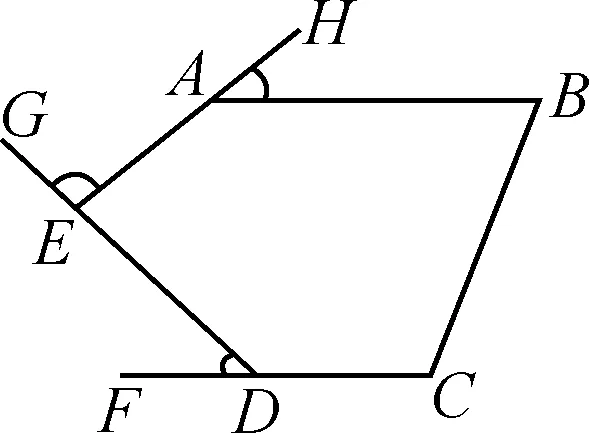
图1

分析：本题若从常规思路解决问题，需要分别求∠HAB，∠GEA，∠EDF的值，再进行求和计算.观察题干，我们可以发现单从现有条件无法分别求出三个角的具体度数.但是，倘若我们运用整体的思想，将∠HAB+∠GEA+∠EDF看成一个整体，问题便迎刃而解.首先，根据多边形内角和公式，求得五边形的内角和为540°.又因AB∥CD，可知∠B+∠C=180°.而∠HAB+∠GEA+∠EDF+∠BAE+∠AED+∠EDC=180°×3=540°，其中∠BAE+∠AED+∠EDC=540°-180°=360°，我们将∠HAB+∠GEA+∠EDF看成一个整体，因此可得∠HAB+∠GEA+∠EDF=540°-(∠BAE+∠AED+∠EDC)=180°.

由此可知，在求解某些几何与图形的问题时，不应执拗于计算出其中某部分具体的值，而应当用“集成”的眼光去看待这些图形，尝试着将部分图形看成一个整体，建立起局部与整体的联系.另辟蹊径将原本不规则的图形变成规则图形，为原本看似无关的部分建立起整体联系，力求更加快速、简单地解决问题.

5 整体思想在函数与图象中的应用

例5已知y+m与x-n成正比例(其中m，n是常数)，求证:y是x的一次函数.

分析:本题需先将y+m和x-n当作一个整体，设y+m=k(x-n)，其中k为不等于零的常数.整理，得y=kx-(kn+m).由于k≠0，并且k，-(kn+m)都为常数，故证得y是x的一次函数.

6 总结

总而言之，解题的目的在于锻炼思维与提升能力.而整体思想作为数学解题思想中的重要组成部分，在数与式子、方程与不等式、图形与几何、函数与图象等问题的解决中，都发挥着重要的作用.整体思想的理解与掌握，不仅能够帮助学生简便快捷地解决问题，还能够在整体解决问题的过程中提升创造性思维.因此，教师在教学中不仅要教会学生如何解决这类问题，更应该引导学生乐于总结，勤于反思，在解决问题的过程中能够挖掘问题中蕴含的理论精华，感受其内含的数学思想.以期学生在今后的学习过程中，能够自主地运用数学的整体思想走出困境，达到事半功倍的效果.