问题引领课堂 促进思维生长*
——以“多边形的内角和”教学为例
⦿广州开发区中学 党小磊
1 背景介绍
《义务教育数学课程标准(2022年版)》中提出:“课堂教学是全体师生共同参与、交流互动、共同成长的活动.”在教学实践中,采用问题串的方式开展课堂教学就是教师与学生的一个互动沟通与课堂反馈的方式[1].下面以“多边形的内角和”为例,展示笔者的课堂教学实践与反思,供同仁研讨.
2 教学过程
2.1 创设情境,激发探究欲望
问题1在2022年二月亚洲杯中,中国女足战胜日本队捧起了冠军奖杯,成了中国人的骄傲.大家都知道足球表面由32个多边形组成,一般是12块黑色正五边形和20块白色正六边形.请问正五边形与正六边形的内角和分别为多少?
教学说明:足球是学生非常喜欢的一项运动,也是中考体育考试选项之一.从学生最关心的问题出发,充分调动了学生探索问题的欲望.体现数学就在身边的同时,设置悬念,找到知识的生长点,可以提升本节课的有效性.中国女足堪称“铿锵玫瑰”,这是每一位中国人的光荣,由此在学生掌握数学知识的同时,也潜移默化地激起他们的爱国主义情感.
2.2 温故知新,发挥引导作用
问题2(1)三角形的内角和等于多少度?
(2)正方形、长方形的内角和各是多少度?
教学说明:本环节问题是巩固已有的相关知识,给学生小小的成功感.“三角形的内角和等于180°”,对接下来探究复杂多边形内角和的分割方法提供了方向.问题2(2)特殊四边形的内角和等于360°,有助于下面问题3(1)的猜想,并同时激励着学生积极投入到一般四边形内角和的探究中,从而在课堂教学中产生正面效应.
2.3 渐次展开,提出数学问题
问题3(1)猜一猜:任意四边形(如图1)的内角和等于多少度?

图1
(2)你有哪些方法能够证明你的猜测?你能找出几种方法?
(3)对比并观察这些分割方法有什么相同和不同?
教学说明:对于问题3,辅助线方法即连接对角线把四边形划分为两个三角形,把四边形的内角和问题转化为两个三角形的内角和,化未知为已知,这是学习数学的一种思想——转化思想,笔者借助问题串达到了教学目标.问题3(1)可由正方形、长方形这两种特殊的多边形的内角之和猜测出任意四边形的内角之和为360°.问题3(2)通过添加辅助线,只要把四边形转化为三角形,就可以求出任意四边形的内角之和,“转化”的数学思维方式已向学生全面渗透.教师在此引导学生通过多种分割四边形成三角形的方式,感受解决方式的多样化.
对于任意四边形,可以利用以下方法分割:
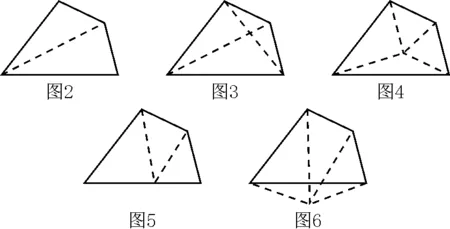
(1)连接1条对角线,可以得2个三角形,如图2,四边形的内角和为2×180°;
(2)连接两条对角线且在四边形内部交于一点,得到4个三角形,如图3,四边形的内角和为4×180°-360°;
(3)若在四边形内部任取一点,如图4,也可以得到相应的结论;
(4)也可在边上任取一个点,如图5,四边形的内角和为3×180°-180°;
(5)还可在四边形的外部取一点,如图6,四边形的内角和为3×180°-180°.
在此,教师引导学生通过不同的辅助线,合作探寻出多种方法,体现了此探索活动的多样化和开放性.问题3(3)旨在通过观察、思考、总结添加辅线的多种方式的共性与区别,促使学生体会:只要把四边形划分为已经知道内角和的图形形状,就可以求出其内角和.一般方法是:从一点开始,通过连接各顶点,将四边形分割为三角形来加以解决.但这个“一点”可以是平面内的任何一点.由此突破难点,将知识上升到思维方式,将未知转化为已有思维方式.
2.4 探索公式,深化转化思想
问题4(1)选择一个你最喜欢的上述分割方法,能否解决问题1中足球表面的正五角形、六边形各自的内角和?
(2)n边形的内角和怎样表示呢?
(3)几种推导多边形内角和的方法中,你觉得哪一种办法最佳?为什么?
(4)对于n边形的内角和,大家得到的算式可能不同,那么得到的结果能一样吗?
教学说明:问题4(1)为了使学生通过增加多边形的边数,再一次体验转化的过程,从而提高学生对转化思想的掌握程度.在正四边形的基础上,探讨边数为整数的正多边形的内角和与边数之间的联系.问题4(2)将任意多边形转化为三角形的方式,有助于锻炼学生的想象能力.而通过对多边形内角和问题的思考,则能够帮助学生总结出多边形的内角和的各种表达式,从而感知数形间的联系,进而体会从特殊到一般的逻辑推理过程.不同的方法可以得到不同的内角和公式,如(n-2)×180°,180°n-360°,180°(n-1)-180°.问题4(3)是最优化的思维,在日常生活中也往往会遇到同一个问题同时有多种处理方式的情形,因此指导学生要“三思而后行”,选择最优最有利于解决问题的方式后再行动.问题4(4)通过逆用乘法分配律进行推理,促使学生感受化归的基本思想,并通过公式的化归过程,进一步感受数形间的联系以及各种方法之间的联系.
180°n-360°=180°n-2×180°=(n-2)×180°,180°(n-1)-180°=180°(n-1)-180°×1=(n-2)×180°.
2.5 运用新知,解决实际问题
问题5(1)八边形的内角和为______.
(2)已知一种多边形的内角和为1 980°,求这种多边形的边数.
(3)已知一个多边形的每个内角均为150°,求这个多边形的边数.
教学说明:该环节引导导学生利用多边形内角和公式解决问题,使他们体会n边形内角和公式在何时能够顺向使用,何时逆向使用,即已知边数求多边形的内角和—直接使用公式,已知多边形的内角和求边数—逆向利用公式的方法.此环节笔者可以及时了解学生的学习效果,让学生经历用知识解决问题的过程.
2.6 学以致用,回归生活情境
问题6关于小亮的一种设想:2024年奥林匹克运动会将在法国举行,他认为设计一种内角和是2 024°的多边形图案将会非常有趣,你觉得小亮的设想能做到吗?
教学说明:多边形的内角和公式即为(n-2)×180°,由此可知多边形的内角之和是180°的正整数倍,显然小亮的设想不成立.通过此环节,学生进一步了解并灵活运用多边形的内角和公式,同时也感受到数学的趣味性以及数学与现实生活的密切关系.
2.7 归纳总结,形成知识体系
问题7这节课你学会了什么?这节课学习的内容对你今后的学习有何启发?
教学说明:本环节意在指导学生总结本节课程的知识内容,把新学习的主要知识点纳入新的知识体系,不断丰富自己的知识.帮助学生发现自身的进步,为进一步深入掌握新知识点形成正向迁移,也为以后的学习打下基础[2].
3 教学反思
本节教学根据多边形的内角和情境,以问题串的方式指导学生进行探究性学习,问题指向性清晰明确.课堂既围绕着某一问题进行,又生长了新的问题.从基础知识层次逐步转入能力素质层次,将整堂课程的教学环节与问题串成一线,不同环节的过渡也更加自然,从而加深了前后问题的联系,既启发了学生的深度思维,又使学生乐此不疲地投入到了课堂学习之中,有效地提高了学生的数学思维能力.
这节课的亮点就是整个课堂自始至终由问题贯穿,师生、生生互动也由始至终.学生在问题串的带动下积极、踊跃、有效地学习,整节课充满生机,实现了预定的教育任务,达到了预期效果.本节课让笔者感受颇深,也让笔者对利用问题串形式开展课堂教学有如下思考.
3.1 问题串有助于建构课堂的整体性
问题串既能较好地反映出整节课的内容,也能较完整地展示整节课的“骨架”[3].本节课从七个问题勾勒出了这节课的整体架构:问题1通过设计当下学生关心的实际情境问题,调动他们学习数学的积极性,设置悬念,引入课题;问题2在问题1的情境下,有助于激活学生现有的数学知识;问题3在问题2的基础上,从特殊到一般,提出与本节课相关的问题,引导学生对新问题进行思考与猜想,通过亲自动手探索多种途径解决问题;问题4是问题3的深入研究,增加图形的复杂性,使学生更深入地感受转化的数学思想,进一步了解转化的实质过程——将多边形转化为三角形,体会到将复杂图形转化为已有知识经验的过程,并在小组学习交流中,共同整理出复杂多边形的内角和公式及最优表达式,从而切身感受到学习的真谛;问题5灵活运用多边形的内角和公式解答问题;问题6运用教学新知探讨并解答生活中的具体问题,使学生对多边形的内角和公式有深入的认识和了解,也感受到数学的魅力和简洁美;用问题7归纳总结本节课的同时,顺势延伸学生的思维生长点,为接下来的学习做好铺垫,也把本节课的知识内容完整地整合在一起.
3.2 问题串有助于激发学生的思维生长
本节课通过精巧的问题设计,不断追问,引导学生勇于猜想、勇敢探索,引导他们继续探索、扩大视野,不断拓展思维[4].一系列问题串由浅至深、层层递进、循序激发学生的深度思考,推动了学生的思维进程,师生之间的交流互动更是体现了探究的思维过程.问题3指导学生利用现有的知识与数学思想展开思维碰撞,生生间、小组间产生思想交流的火花;问题4指导学生把问题的实质从复杂的图形中剥离开来,化繁为简;问题5为更好地挖掘学生的数学思维能力,从公式的顺向与逆向理解多方位设置练习,以化解学生在公式运用上的思想阻塞点;问题6引导学生拓展思维,直击学生的思维深处.整节课的教学重点不是放在公式的大量练习上,而是定位在多边形的内角和公式形成的探索过程,这是注重培养学生思维能力的表现,对学生的思维提升大有裨益,也有助于更好地促进学生的思维生长.

