n阶α次积分C半群的逼近

刘乔乔，赵华新

（延安大学数学与计算机科学学院，陕西延安 716000）

算子半群的逼近定理是各类算子半群研究的重要内容，近年来，对算子半群理论的研究取得了显著的成果。文献［1-4］讨论了指数有界C半群、双连续C半群以及双参数C半群的生成、逼近及紧性等相关问题；文献［5］研究了n次积分C半群的定义及相关性质；文献［6-9］研究了α次积分C半群的Trotter-Kato逼近定理和概率逼近问题，以及指数有界双连续α次积分C半群的逼近等相关问题；文献［10-11］引入了n阶α次积分C半群及其次生成元，给出了n阶α次积分C半群的定义、预解式、预解方程等相关性质，并解决了Cauchy问题；文献［12-17］研究了单参数n阶α次积分C半群的相关性质、双参数n阶α次积分C半群的定义、逼近定理等相关性质及多参数n阶α次积分C半群的预解集，将单参数n阶α次积分C半群推广到双参数n阶α次积分C半群及多参数n阶α次积分C半群。在上述研究基础之上，n阶α次积分C半群的相关性质还有一些未被研究。本文通过借助算子半群逼近的相关理论及经典算子理论的研究方法，给出n阶α次积分C半群的逼近定理并证明，从而进一步完善了n阶α次积分C半群的相关理论。

1 基本概念和引理

X为无限维的复Banach空间，B(X)是X上有界线性算子全体所成的Banach代数。T(t)∈B(X)，t≥0，D(A)为线性算子A的定义域，设n∈N，α≥0，

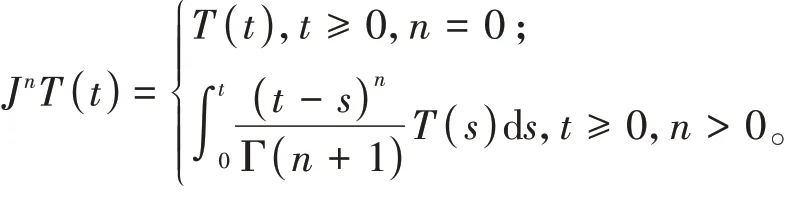
易知T(t)=0当且仅当存在n＞0，使得J n T(t)=0，t≥0。

定义1［10］设n∈N，α≥0，C∈B(X)是单射，{T(t)}t≥0⊂B(X)强连续，若存在闭线性算子A使得

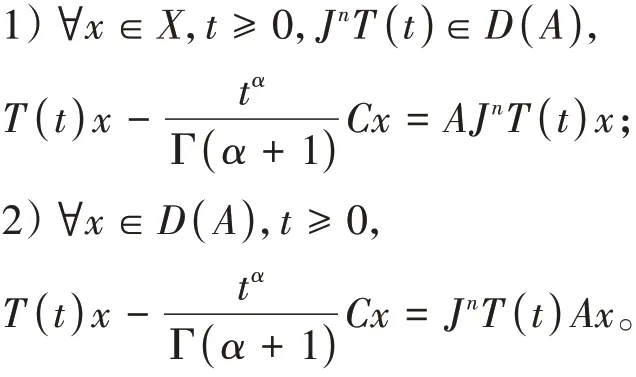
定义2［11］若R c(λ，A)=λn-1(λn-A)-1C有定义在Banach空间X上的有界逆算子，则称λ为n阶α次积分C半群的次生成元A的正则点，R c(λ，A)为A的C预解式，正则点的全体称为A的C预解集，记为ρc(A)。

引理1［11］令n∈N，α≥0，C∈B(X)是单射，A：D(A)⊂X→X为闭线性算子并满足A⊂C-1AC，{T(t)}t≥0⊂B(X)强连续并满足‖T(t)‖≤Meωt，t≥0，ω≥0，M＞0，可得下列命题等价：

1）n阶α次积分C半群{T(t)}t≥0的次生成元为A；

2）{λn|Reλ＞max{ω，0}}⊂ρc(A)，并满足下式

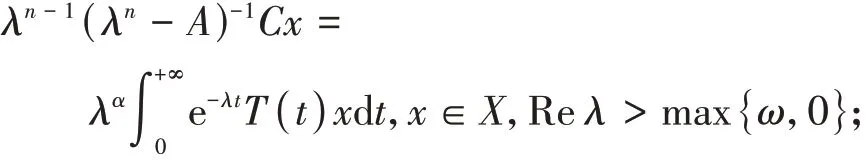
3）{λn|λ＞max{ω，0}}⊂ρc(A)，并满足下式

引理2［11］令n阶α次积分C半群{T(t)}t≥0的次生成元为A，并且{T(t)}t≥0∈Gτ(M，ω，C)，其中ω≥0，M＞0，C∈B(X)，则∀x∈X，有

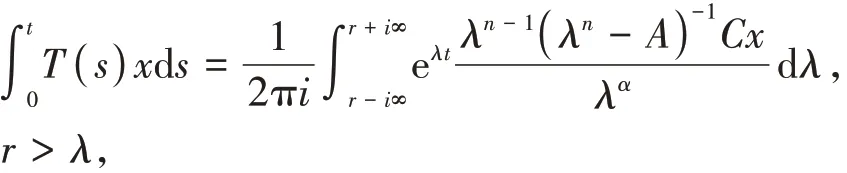
∀x∈D(A)，有

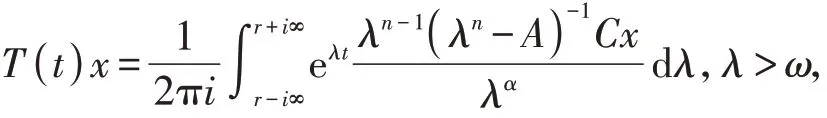
而且两式的右端积分在关于t的有限范围内是一致收敛的。

2 主要结果

定理1设A，A n∈G(M，ω)，{T(t)}t≥0，{T n(t)}t≥0分别是由A，A n次生成的n阶α次积分C半群，若∀x∈X，t≥0，T n(t)x→T(t)x(n→∞)，则有∀x∈X，Reλ＞ω，R c(λ，A n)x→R c(λ，A)x(n→∞)。

证明设∀x∈X，t≥0，

T n(t)x→T(t)x(n→∞)。

根据预解式的定义及引理1，对Reλ＞ω有

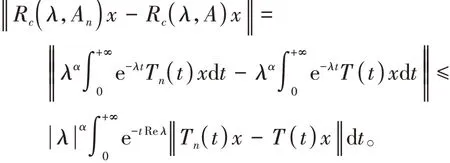
上式两边取极限得

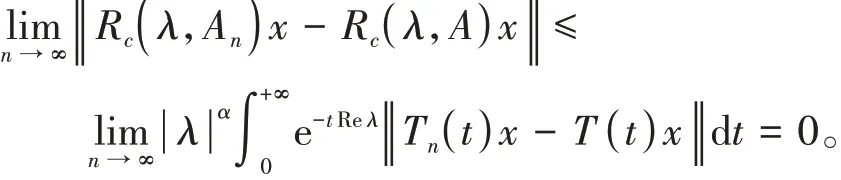
即∀x∈X，Reλ＞ω，有

R c(λ，A n)x→R c(λ，A)x(n→∞)。证毕。

定理2设A，A n∈G(M，ω)，{T(t)}t≥0，{T n(t)}t≥0分别是由A，A n次生成的n阶α次积分C半群，若∀x∈X，Reλ＞ω，R c(λ，A n)x→R c(λ，A)x(n→∞)，则有∀x∈X，t≥0，T n(t)x→T(t)x(n→∞)。

证明∀x∈X，在一固定区间t∈[0，T]上有

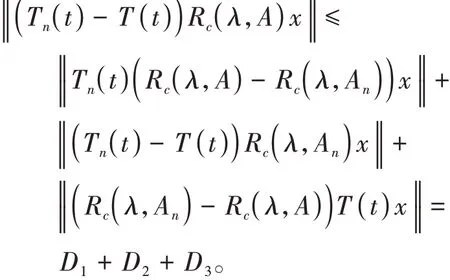
1）关于D1

由 于‖T n(t)‖≤Meωt≤MeωT，∀x∈X，Reλ＞ω，R c(λ，A n)x→R c(λ，A)x(n→∞)，有

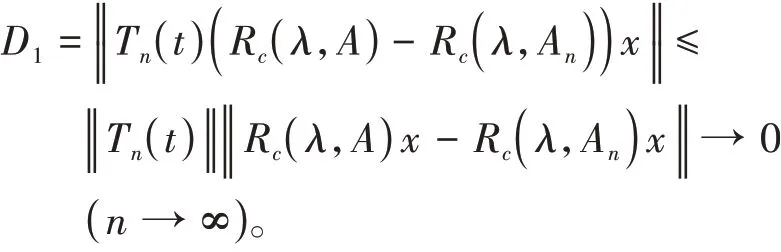
即D1→0。

2）关于D3

因为T(t)x是关于t连续的，所以T(t)x将紧集[0，T]映射成紧集，{T(t)x：0≤t≤T}是紧集。

又由于∀x∈X，R c(λ，A n)x→R c(λ，A)x(n→∞)，则对T(t)x∈{T(t)x：0≤t≤T}有

R c(λ，A n)T(t)x→R c(λ，A)T(t)x(n→∞)。

即D3→0。

3）关于D2

由引理2知

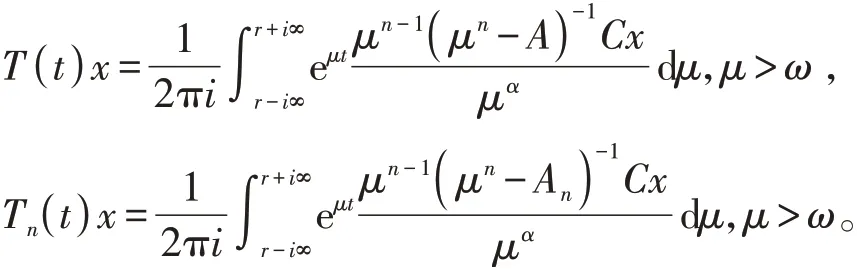
则有

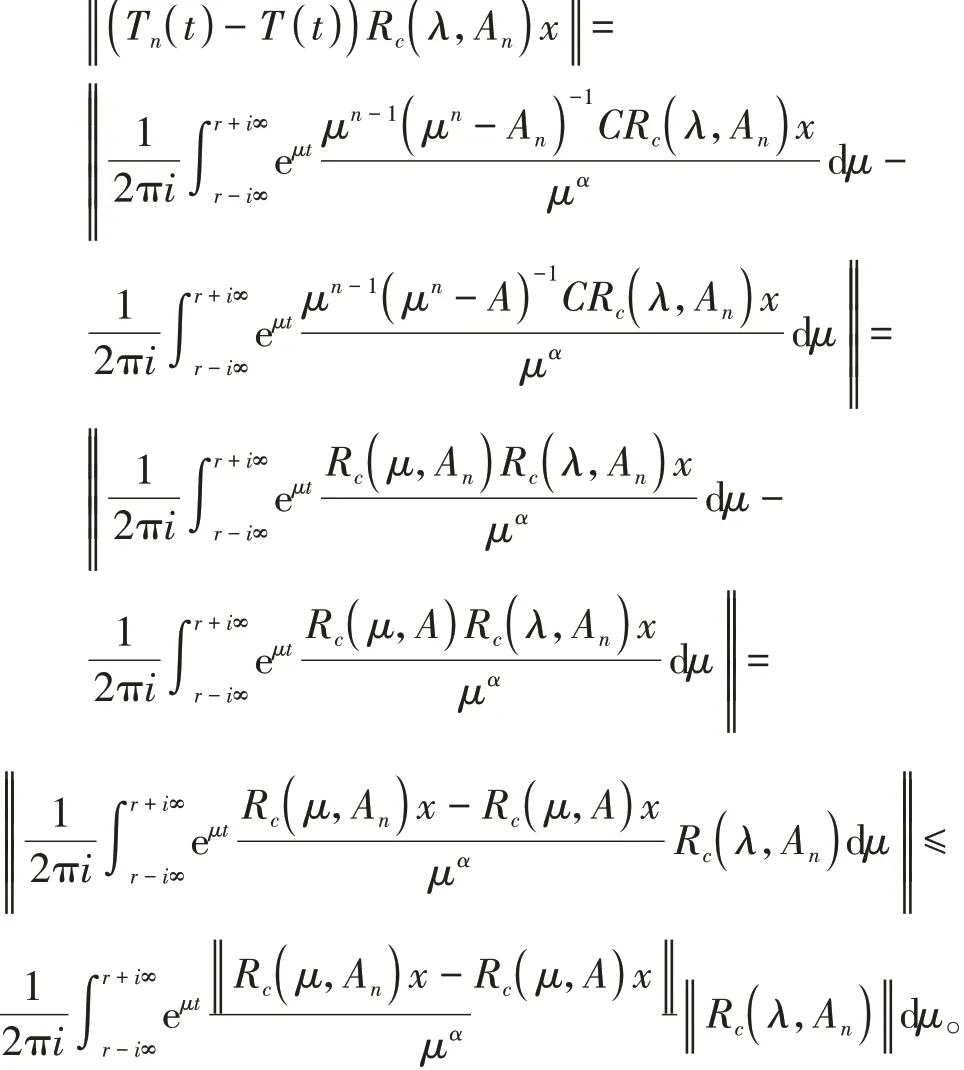
由已知条件知：当n→∞时，

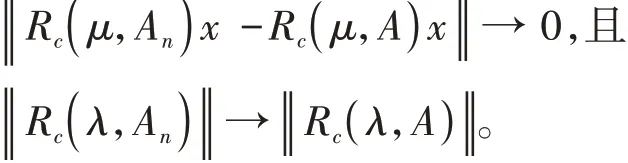
从而有

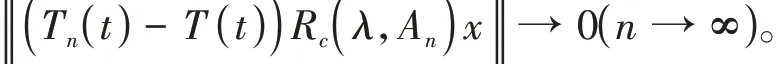
即D2→0。

从而∀x∈X，当n→∞时，

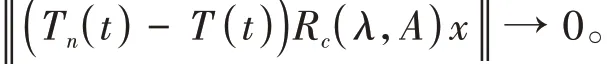
∀x∈D(A)，可以表示成x=R c(λ，A)z的形式，其中z∈X。所以∀x∈X，

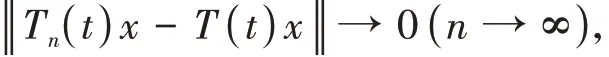
即T n(t)x→T(t)x(n→∞)。证毕。