在“说理”训练中发展小学生的推理能力——以人教版小学数学第九册“组合图形的面积”教学为例

王燕霞 吴丽红

（晋江市第三实验小学，福建 晋江 362200）

推理是数学的基本思维方式，也是人们学习和生活中经常使用的思维方式。［1］推理能力是借助推理的数学思维方式以解决问题的能力，是小学数学中的核心能力，应贯穿于整个数学学习过程中。数学说理是指运用数学语言进行逻辑表达的过程，既是推理思维物化外显的主要形式，也是促进学生推理能力进步的必然途径。［2］本文以人教版小学数学第九册“组合图形的面积”为例，谈谈在“说理”训练中培养学生推理能力的实践与思考。

一、以学习任务为依托，创设推理空间

在数学“说理”教学中，教师通过设计学习任务，引导学生积极探索，经历观察、猜测、计算、推理、验证等活动，追溯数学知识的本源，促进学生进行逻辑推理思考，为发展学生的逻辑推理素养提供脚手架。［2］例如，“组合图形的面积”一课，通过任务学习单的设计，逐步引导学生通过观察图形的特点，创设“正确计算出组合图形面积”的推理空间。

任务1：观察“L”图形（如图1），估一估它的面积大约是多少？

图1

任务2：你能想办法求出它的面积吗？

建议：画一画，把你的思考过程在图中画出来。算一算，计算组合图形的面积。

推理能力培养的前提和必要条件在于学生产生认知困惑。通过学习任务1 的设计，学生发现“L”图形和所学过的图形都不相同。而任务2 的设计，主要是让学生通过多途径获取信息、得到依据，然后展开后续的推理。在独立计算组合图形的面积时，学生会主动根据图中提供的4 个数据进行分析，与旧知识联系，将组合图形转化成已学过的基本图形进行计算。这是一种信息处理能力，是推理能力形成的基础，是推理有依据的前提。学习任务的设计，为学生讲清楚计算组合图形面积的道理，感受解题策略的多样性，渗透转化推理能力提供了真实的素材，创设了自主推理的空间。

二、以“说理”活动为渠道，习得推理方法

启发学生说理，是培养推理能力初级教学阶段最主要的手段与基本途径。［3］与推理能力密切相关的思维习惯，主要是有根有据、有条有理地思考与表达。［3］因此，教师要重视说理活动的挖掘与利用，将推理能力的培养和课堂说理活动有机结合起来，通过适当地开展说理训练，让学生观察、分析、判断，再通过推理寻找答案，感受推理作用，体验推理价值。

（一）借“直观”说理，使思维可见化

以丰富的感性材料为载体，引导学生动手操作并进行较复杂的认知活动，把数学道理隐藏其中，使学生获得对事物的具体的、感性的认识。再通过“画一画”，让学生把思考过程“显现”出来（如图2）。运用直观操作画出辅助线，能将学生内隐的想法外显出来，让思考过程可见，既减少抽象理解的困难，又促进学生知识理解内化。

图2

（二）用“交流”说理，语言表达逻辑化

课堂中生生互动交流是说理训练的最佳时机。教师可引领学生学会用有理、有据、有序的语言表达推理的过程，增强推理的逻辑性。如计算组合图形的面积时，当学生面对学习任务充分独立思考后，利用交流话题，引导学生在小组内交流。

例如，计算这个组合图形的面积（如图3），你会用哪种方法？请说一说想法。

图3

A.3×7+（6-3）×4

B.4×6+（7-4）×3

C.6×7-（7-4）×3

D.（7+4）×6÷2

在探索、交流中，教师应着力提倡学生利用关联词表达想法。如用这样的语言描述：如果把组合图形分成上下两个长方形，那么可以用方法A 解答；如果把组合图形分成左右两个长方形，那么可以用方法B解答；只要先把长方形添补完整，再去掉空白的正方形就是图形的面积；因为方法D 是梯形的面积计算公式，所以应该把组合图形转化成一个梯形……在解读各种解法的过程中，学生深入地体会到合理分割、添补的方法是求组合图形面积的重要策略。其中，方法D 对学生的思考要求更高（如图4）。教师不仅要让他们猜想“这是怎么想的”，更要引导他们验证“为什么可以这样想”，突出猜想与验证的小心求证环节，逐步建构自己能接受的数学推理方式。

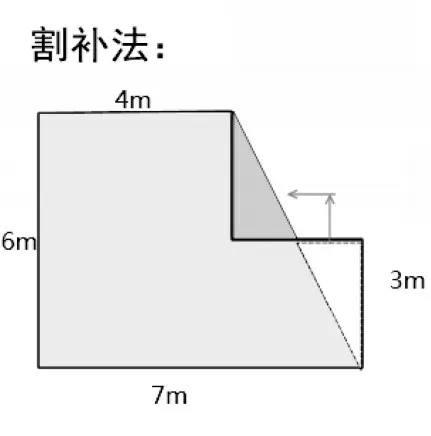
图4

三、以“说理”习题为载体，发展推理能力

（一）基础练习，积累推理经验

在数学教材中蕴含着大量的推理素材，教师要注重挖掘与利用，将推理能力的培养和四大领域有机结合起来。利用基础练习举一反三，是循序渐进提高学生推理能力的好方法。通过设计精准合理的练习题目，引领学生主动积累推理经验。

基础题：2021 年是少先队建队72 周年，淘气、笑笑和奇思准备做一面中队旗（如图5）。他们用以下3种方法，计算做一面中队旗需要多少平方厘米红布。他们的方法对吗?请说明理由。

图5

上述基础作业，旨在通过说理训练，让学生内化计算组合图形的策略，知道分割求和、添补求差、割补等方法也适用于一般的组合图形，感悟同类事物的各种特殊情形中蕴含的同一性和相似性，明白从特殊到一般的推理过程，提高归纳推理能力。

（二）变式练习，融通推理方法

除了教材现有素材外，教师还可借助教材题目，改编或创编问题，提供变式练习，适当地开展推理训练，引导学生解决生活和数学中的问题。

选做题：1.把上面的方法和下面相应的算式用线连起来，并说明理由。

①6×8-（5+8）×3÷2 ②3×5+（3+6）×3÷2

③3×8+3×3÷2 ④（5+8）×3÷2＋6×3÷2

2.两个相同的直角三角形重叠在一起（如图6），求阴影部分的面积是多少?并说一说，你是怎样想的？（单位：cm）

图6

以上两题，学生可根据自己的能力选做。此类题目，让学生的思维向深度、广度拓展，养成“观察—猜想—论证”的思维习惯。学生运用最常见的推理方法——转化，把复杂问题转化为简单问题，把未知问题转化为已知问题，同时发展演绎推理思想，提高推理能力。