高层建筑室外架空燃气立管的应力分析

白 剑

(山西省燃气规划设计研究院有限责任公司，山西 太原 030024)

在高层建筑燃气供应系统设计中，由于温差产生的管道变形是一个不容忽视的问题。尤其是当燃气立管敷设于建筑物外墙时，由于夏季室外气温高、日照时间长，不具备保温的燃气管道在长时间暴晒下，管道温度会很高。根据《城镇燃气设计规范》GB50028-2006[1]，当管道沿外墙和屋面敷设时，补偿量计算温差可取70℃。如果将管道两端固定，则热膨胀应力将会很大，超出管道的许用应力。因此，需对管道的热膨胀进行补偿。采用将管道两端固定并在中间安装吸收变形的挠性管或波纹补偿装置的方式来补偿由于温差产生的胀缩变形[2]。

1 室外架空立管的物理模型

通过室外架空立管引入户内厨房的高层建筑燃气供应系统简化模型如图1所示。OAn为室外架空立管(长臂)，AnBn为入户支管(短臂)，OAnBn管系形成一个简单的L型自然补偿结构。做如下假设：

图1 高层建筑燃气供应系统简化模型

(1)O点和Bn点为固定点。

(2)An点的热胀位移始终在纵向，无横向的位移。

(3)忽略短臂AnBn的热胀效应。

本文将分三步对该模型进行分析。

(1)已知AnBn的长度为l，计算垂直作用于自由端An点允许的最大集中力Fnmax及An点的挠度ω。

(2)已知OAn，A1A2，A2A3…An-1An的长度为L1，L2，L3…Ln，分别确定垂直作用于自由端A1，A2，A3…An点的集中力F1，F2，F3…Fn与位移量的关系ΔX1，ΔX2，ΔX3…ΔXn。

(3)由Fn≤Fnmax确定长臂最大长度Lmax。

2 模型分析

(1)AnBn为悬臂梁模型，如图2所示。

图2 悬臂梁模型

考虑短臂重力的影响，根据材料力学得出

求得

式中：F— —垂直作用于自由端A点的集中力，N；I— —管道的惯性矩m4；[σ]— —管道的许用应力，Pa；q— —管道均布荷载，即单位长度的管道重力，N/m；l— —短臂的长度，m；d0— —管道的外径，m。

由此可以得出管道的最大挠度为。

(1)

式中：E— —管材的弹性模量，Pa。

(2)OAnBn为L型管系模型，在忽略长短臂重力影响的情况下对L型管系的应力进行了理论分析，通过数值计算得出了短臂的值,并得出OAnBn管道的危险点为Bn点[3]。同时以公式(2)为基础给出了L型管系长短臂之间的关系[1]。

ΔX-ΔXF=ω。

其中

ΔX=L1-n·αΔt

。

(2)

(3)

针对本文中提到的室外架空立管模型，假设立管在第n个支管处的位移最大，其方程如下。

ΔX-ΔXF1-ΔXF2-…-ΔXFn=ω

。

(4)

将式(1)(2)(3)代入(4)中得出

(5)

其中

F=F1+F2+…+Fn。

解得

(6)

(7)

式中，F— —所有短臂支管对长臂的作用力合力，N；Fn— —垂直作用于第n个短臂支管作用力，N；Ln— —第n个短臂支管与第n-1个短臂支管之间长臂的长度，m；L1～n— —长臂从最下端固定点至第n个短臂支管之间的长度，m；Δt— —补偿量计算温差，取70℃;G— —长臂的重力，N；A— —长臂管道的横截面积，m2；n— —短臂支管的个数；l— —短臂支管的长度，m。

(3)针对室外架空立管引入户内厨房的高层建筑燃气供应系统，通过比较所计算出的作用力Fn(或支管起点垂直位移量)和允许的最大作用力Fnmax(或支管允许的最大挠度)的大小，以确定长臂设置补偿装置的位置。

3 参数影响分析

通过前文的分析，架空管道的受力分析需计算出两个力，分别为垂直作用于第n个短臂支管作用力Fn和第n个短臂支管自由端允许的最大作用力Fnmax。从公式中可以看出，影响Fn的参数主要有支管之间的间距L1、短臂的长度L2、长臂管道的外径d1及壁厚t1、短臂管道的外径d2及壁厚t2、选用温差ΔT等。一般高层住宅、入户管道之间的间距L1均为定值，多为2.9m。而影响Fnmax的参数主要为短臂的长度L2、短臂管道的外径d2及壁厚t2等。针对以上几个参数影响，本文选取不同工况进行计算分析。

3.1 Fnmax的参数影响分析

本文选取三个工况进行计算分析。

工况一：d2=27mm，t2=3mm，L2分别为0.5m，0.6m，0.7m，0.8m，0.9m和1m的情况下Fnmax的计算值。计算结果见表1。

表1 Fmax随L2的变化表

工况二：t2=3mm，L2=1m，d2分别为27mm，34mm，42mm，60mm，76mm和89mm的情况下Fnmax的计算值。计算结果见表2。

表2 Fmax随d2的变化表

工况三：L2=1m，d2=27mm，t2分别为3mm，4mm，5mm，6mm，7mm和8mm的情况下Fnmax的计算值。计算结果见表3。

表3 Fmax随t2的变化表

通过以上三种工况分析，针对悬臂梁模型、短管一端固定，另一端受力，随着短臂长度的减小，管径的增大及壁厚的增加，短管自由端所能承受的推力逐渐增大。

3.2 Fn及n的参数影响分析

本文选取七个工况进行计算分析。

工况一：L2=1m，d1=60mm，t1=4mm，d2=27mm，t2=3mm，ΔT=60℃，L1分别为2.8m，2.9m，3m，3.1m，3.2m的情况下Fn的计算值。计算结果见表4。

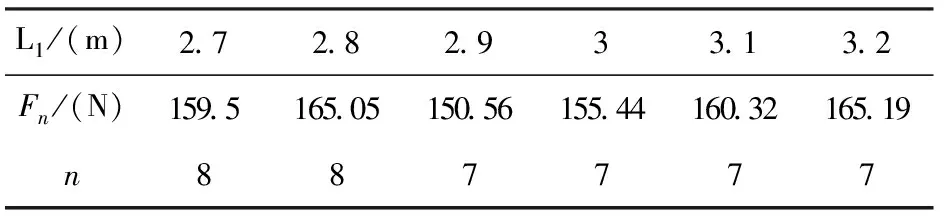
表4 Fmax及n随L1的变化表

工况二：L1=2.9m，d1=60mm，t1=4mm，d2=27mm，t2=3mm，ΔT=60℃，L2分别为0.5m，0.6m，0.7m，0.8m，0.9m和1m的情况下Fn的计算值。计算结果见表5。

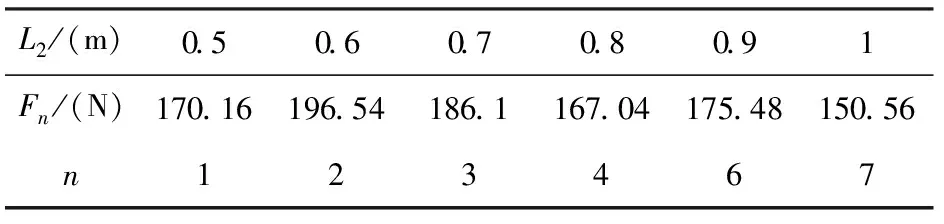
表5 Fmax及n随L2的变化表

工况三：L1=2.9m，L2=1m，t1=4mm，d2=27mm，t2=3mm，ΔT=60℃，d1分别为34mm，42mm，48mm，60mm，89mm和114mm的情况下Fn的计算值。计算结果见表6。

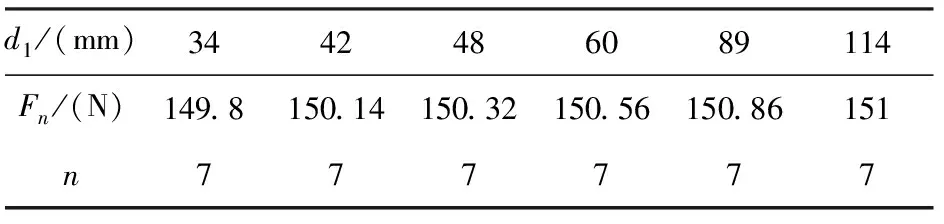
表6 Fmax及n随d1的变化表

工况四：L1=2.9m，L2=1m，d1=60mm，d2=27mm，t2=3mm，ΔT=60℃，t1分别为3mm，4mm，5mm，6mm，7mm和8mm的情况下Fn的计算值。计算结果见表7。

表7 Fmax及n随t1的变化表

工况五：L1=2.9m，L2=1m，d1=60mm，t1=4mm，t2=3mm，ΔT=60℃，d2分别为27mm，34mm，42mm，60mm，76mm和89mm的情况下Fn的计算值。计算结果见表8。

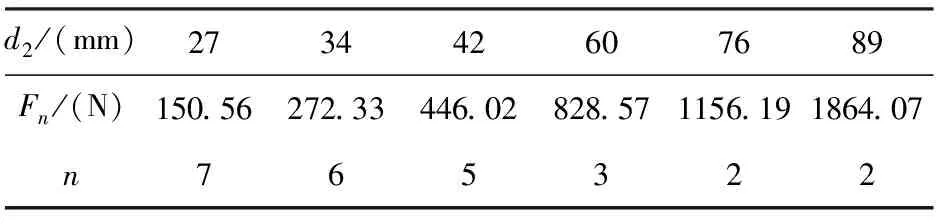
表8 Fmax及n随d2的变化表

工况六：L1=2.9m，L2=1m，d1=60mm，t1=4mm，d2=27mm，ΔT=60℃，t2分别为3mm，4mm，5mm，6mm，7mm和8mm的情况下Fn的计算值。计算结果见表9。

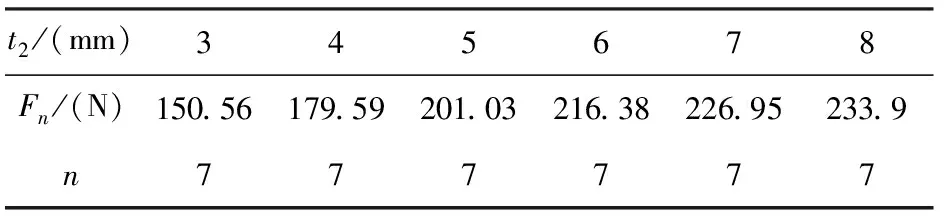
表9 Fmax及n随t2的变化表

工况七：L1=2.9m，L2=1m，d1=60mm，t1=4mm，d2=27mm，t2=3mm，ΔT分别为20℃，30℃，40℃，50℃，60℃和70℃的情况下Fn的计算值。计算结果见表10。

表10 Fmax及n随ΔT的变化表

通过以上七种工况分析，随着支管之间的间距L1、短臂管道的外径d2、选用温差ΔT的的增大，短臂的长度L2长度的减小，承受最大作用力的支管位置越靠下；随着长臂管道的外径d1及壁厚t1、短臂管道壁厚t2的增大，同一位置支管所能承受的作用力越大。

4 计算实例

对于某一高层建筑，层高为2.9m，首层支管与立管底端固定点之间的距离为2.5m，设定室外架空立管为D60×4的无缝钢管，许用应力为[σ]=130MPa，弹性模量为E=2.02×105MPa，线膨胀系数为α=1.2×10-5/K，补偿量计算温Δt=70℃，短臂采用D27×3的无缝钢管，长度l=1.2m。

经计算，垂直作用于短臂支管允许最大作用力Fnmax为143.16N，最大挠度0.023m。长臂位于第九层和第十层处垂直作用于短臂支管作用力F9和F10分别为130.88N和144.41N，支管起点的位移量分别为0.021m和0.024m。由此考虑采取相关措施，以限制第九层以上的支管起点垂直位移量，如增设补偿装置等。

5 结 语

以材料力学为基础，通过悬臂梁模型和L型管系模型，计算得出室外架空立管引入户内厨房的高层建筑燃气供应系统中F和L，l之间的关系，以此作为室外架空立管补偿装置位置确定的依据。通过分析得出，可通过增加短臂l长度和加大入户管穿墙套管尺寸的方式减少补偿装置数量。