变分回波跟踪算法在武汉汛期临近预报中的适用性

庞 晶，袁 凯，李武阶，李 明，刘佩廷

（武汉市气象局，武汉 430040）

对流天气临近预报通常是指对某一区域雷暴及其产生的灾害性天气未来0～2 h 发生、发展、演变和消亡的预报，在气象灾害防御中具有极其重要的地位。陈明轩等［1］、俞小鼎等［2］和程丛兰等［3］对强对流临近预报方法进行了详细分析和阐述，认为目前强对流天气临近预报主要有以下2 种方法，基于雷达回波的外推技术和数值天气预报技术。数值预报虽然已经在气象领域得到了广泛应用，但仍存在其自身的局限性［4］，特别是在临近预报应用方面，不仅需要复杂的物理计算过程，准确率低，而且在精细化程度方面难以满足业务需求［5，6］，因此，天气雷达仍然是对流天气临近预报的主要工具。业务上应用的临近预报方法主要是基于雷达数据的雷暴识别跟踪和自动化外推预报技术［7］，主要包括单体质心法、交叉相关法和光流法。

单体质心法由于其较大的计算量和只适用于强对流风暴的“先天性缺陷”，导致其预报准确率难以有较大幅度的提高［8］；交叉相关法没有考虑深对流系统通常伴随较强的垂直运动，因此该方法仅适用于缓慢变化的层状云降水系统，对快速增长或消散的强对流系统的预报效果并不理想［9，10］；光流法可以较为准确地得到雷暴的整体运动趋势，但对于热带降水系统尤其是台风系统，光流法没有考虑到雷达回波的旋转性，导致其预报效果不如交叉相关法，此外，其基本模型较实况仍存在不少误差，比如要求图像遵循灰度不变形假设，另外求解光流场时，也只适用于回波运动较小的情况，对于快速移动的回波误差仍然较大［11，12］。

鉴于交叉相关法和光流法外推预报中的不足，近年来，国内外众多学者基于连续时次的雷达资料，采用变分回波跟踪算法（Variational Echo Tracking method，VET）进行强天气临近预报，广泛开展了变分回波跟踪算法在临近预报预警中的应用研究。Michael等［13］利用瑞士雷达资料，分析了2005—2010年20 个夏季强降水事件，结果显示基于变分回波跟踪算法的临近降水预警，要优于欧拉算法和高分辨率的数值天气模式预报结果；吴剑坤等［6］通过对京津冀地区18 个典型对流个例定量检验发现，当雷达回波强度阈值为35 和45 dBz 时，无论是30 或60 min外推预报，变分回波跟踪算法的命中率和临界成功指数都明显高于交叉相关法，且虚警率更低，另外天气类型定量检验发现绝大多数天气类型变分回波跟踪算法外推预报效果优于交叉相关法。本研究尝试将变分回波跟踪算法引入到武汉汛期强天气的预报预警中，检验和评估该算法对武汉雷达回波的临近预报能力，可为武汉雷达回波临近预报提供参考。

1 资料

研究主要用 2021 年汛期（5 月 1 日至 9 月 30 日）武汉新一代多普勒天气雷达组合反射率因子产品，其范围覆盖湖北东部地区的以武汉雷达站为中心、边长为320 km 的正方形区域，其经、纬度分别为113.098°—115.648°E，29.247°—31.797°N，时间分辨率为6 min，空间分辨率为1 km×1 km，雷达回波数据进行了固定地物杂波和超折射回波的抑制［6］。

2 方法

2.1 变分回波跟踪算法基本原理

变分回波跟踪算法由Laroche 等［14］提出，其核心思想为采用变分技术，从连续时次雷达回波资料中反演出运动矢量场，根据反演的运动矢量场对雷达回波进行外推预报。

尽管相邻2 个时次的雷达反射率因子会随时间变化而发生变化，但在短时间内（6 min 内），这种变化可以认为非常微小，因此可以假定雷达回波的运动基本满足拉格朗日守恒，即雷达回波反射率因子在短时间内保持不变。变分回波算法的关键在于采用变分方法，通过极小化某一包含了反射率因子守恒项和平滑约束项的代价函数，得到其最优解，即最终的雷达回波运动矢量场（u，v）。采用的代价函数如下。

式中，FZ为反射率因子守恒约束项，可以用全区域所有点联系时次的反射率因子残差的平方总和代替，其求解表达式如下。

式中，ψZ为反射率因子守恒约束项的权重系数，代表了雷达资料质量，一般整个雷达区域取一个常量；u和v分别是雷达回波在X 和Y 方向上的运动速度；Z(x,y,t0) 为t0时刻的反射率因子，Z(x-uΔt,y-vΔt,t0-Δt)则为t0-Δt时刻的反射率因子。

式（1）中，FV为引入的平滑约束条件项，其作用是限制（u，v）在空间上的可变性，防止得到的（u，v）与周边差异过大，其表达式如下。

式中，ψV为平滑约束条件项的权重系数，一般为常量。

综上可知，代价函数中包含2 个控制变量（u，v），其求解转化为寻找最优的（u，v）使得该代价函数值最小，因此可以采用迭代方法求其最优解。

式中，XN为包含了控制变量（u，v）的第 N 迭代点，dN为第N 次的搜索方向，由代价函数相对于控制变量的梯度计算得到，aN为第N次的步长因子，N为迭代次数。因此，不同的步长因子和搜索方向构成了不同的迭代方法，本研究采用广泛使用的拟牛顿法（L-BFGS 法）［15］，该方法具有计算稳定、收敛快、节省计算开支等优点，特别适合求解大范围无约束优化问题。

具体计算步骤如下。①设定收敛条件，并给出控制变量（u，v）的一个初猜值；②计算代价函数以及代价函数相对于控制变量（u，v）的梯度，按照一定的方法求得搜索方向dN；③确定步长因子aN，使目标值有某种意义的下降；④应用公式（4）计算得到XN+1，如果XN+1满足收敛条件，则停止迭代，得到最优解XN+1，反之如果不收敛，则N=N+ 1，跳至第2步，直到求得最优解。

2.2 检验方法

为了客观衡量VET 算法对雷达回波的外推预报能力，引入气象领域应用较广的3 个评价指标，临界成功指数（Critical Success Index，CSI）、命中率（Probability Of Detection，POD）和 虚 警 率（False Alarm Rate，FAR）［16］，对预报结果进行量化评估，具体检验评分的计算公式如下。

式中，NAk为预报正确格点数，NBk为空报格点数，NCk为漏报格点数，k为检验雷达回波不同强度阈值，采用分阈值的检验方法（分别为20、30、40 和50 dBz），逐个像素点进行检验（表1）。

表1 雷达回波预报分级检验

3 结果与分析

3.1 整体评分

以10 dBz 为回波强度阈值，对14 326 组检验样本2 h 的平均得分（预报时间间隔为6 min）进行再平均，CSI达 0.358，POD为 0.483，FAR为 0.463。Germann 等［17］基于美国雷达组网资料分析变分回波跟踪算法的临近预报研究中得到，CSI在0.3 以上视为有效预报，因此可以看到VET 算法表现出较好的预报能力。从各种评分指标随时间的演变来看（图1），随着预报时效的延长，VET 算法的预报能力逐步下降，表现为FAR的缓慢上升以及POD、CSI的缓慢下降。从变化趋势来看，随着预报时效的延长，预报能力的降幅相对平稳，各指标均表现为48 min 以后变化趋于平稳。以CSI为例，48 min 之前变幅在7%以上，48 min 之后变幅稳定在4.8%～7.0%。

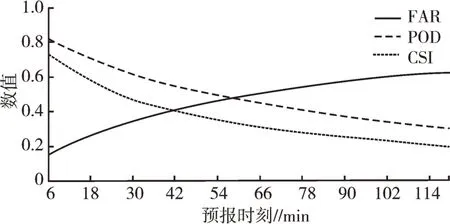
图1 14 326 组检验样本FAR、POD、CSI随时间的演变

为了客观衡量各算法对于不同强度回波的预报能力，进行了不同阈值（≥20 dBz、≥30 dBz、≥40 dBz）回波的检验评估（表2）。整体来看，随着回波强度的增加，CSI和POD都迅速降低，FAR虽然呈下降趋势，但变化幅度在3.5%以内，另外CSI和POD均在30～40 dBz 下降最快，说明其对较强回波的敏感性要强于弱回波。

3.2 不同强度降水过程和不同降水性质的检验评估

王莉萍等［18］利用 1960—2009 年 1 789 个气象观测站的逐日降水资料，统计分析了中国区域降水的时空分布特征暴雨孕灾环境的脆弱性及气象服务需求等，将中国分为4 个暴雨灾害敏感区，并基于降水影响对降水过程进行定义，分析给出了降水强度、覆盖范围、降水持续时间3 个降水过程综合强度的评估指标。参考该评估指标，按照不同降水强度和不同降水性质进行分类，将观测站点的平均降水量（RR）和中雨以上占比（PP）作为分类标准，检验样本分为3 类降水强度类型：弱降水（RR＜10）、中等强度降水（10≤RR＜25）、强降水（RR≥25），2 类降水性质类型：分散性（PP≤20%）、区域性（PP≥70%）。

3.2.1 不同强度降水过程的检验评估 分别计算不同降水强度各类检验指标（表3），可以看到，POD、FAR、CSI均表现为强降水最优，强降水较弱降水提升幅度分别为15.4%、15.5%、20.3%。

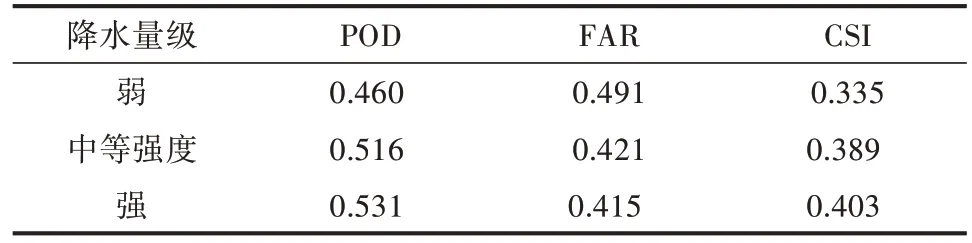
表3 不同降水强度VET 算法评分

从各评分指标随时间的演变（图2）来看，不同降水强度之间各指标值虽然表现不同，但整体趋势较为一致，都表现出FAR缓慢上升以及POD、CSI缓慢下降，同时，中等强度以上降水预报能力明显强于弱降水，而中等强度和强降水之间的差距较小，不同时效各指数差距均在5.5%以内。预报时效120 min以内，POD、FAR、CSI均表现为强降水最优，与弱降水相比，POD提升幅度为3.8%～21.6%，FAR降低幅度为11.3%～20.8%，CSI降低幅度为6.5%～30.7%。

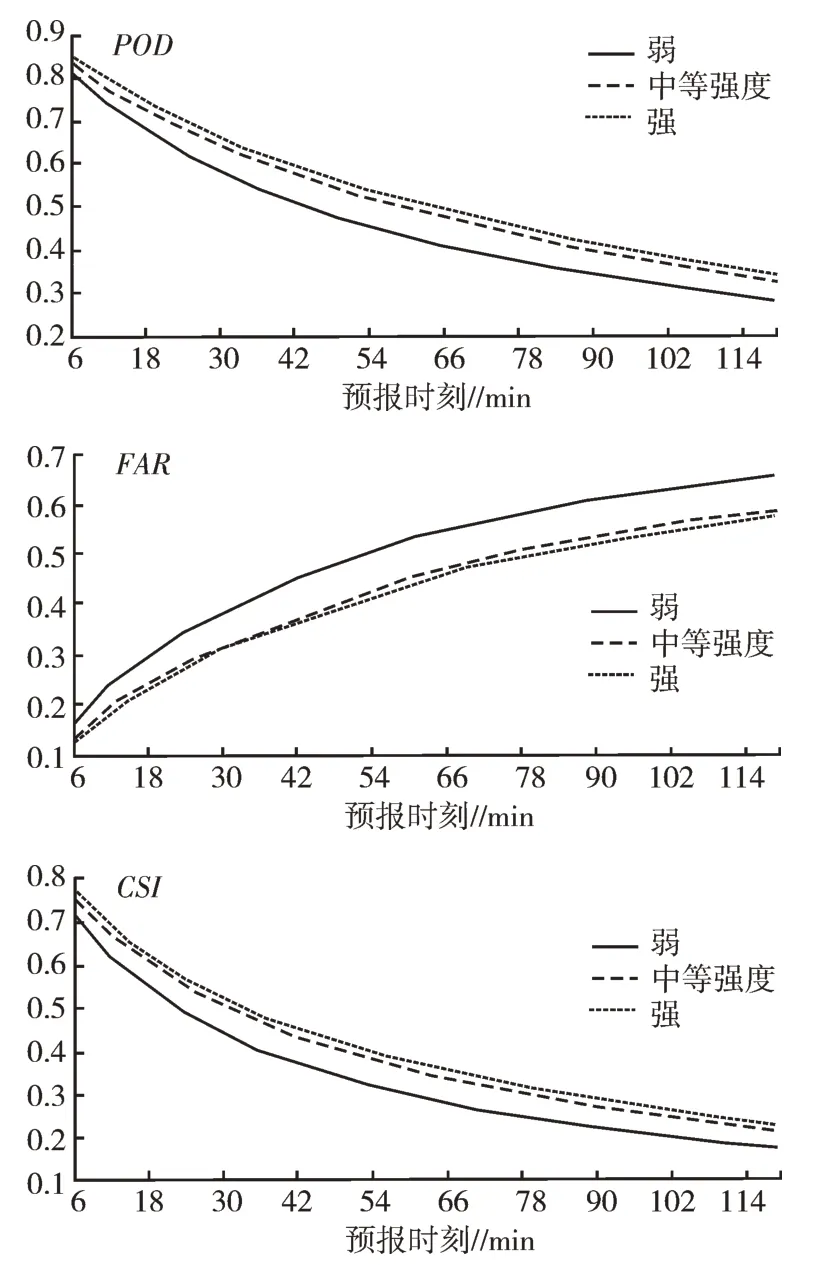
图2 不同降水强度检验样本平均的POD、FAR 和CSI时间演变

同样，进行了不同阈值回波的检验分析（表4）。整体来看，随着回波强度的增加，CSI、POD均逐渐降低，FAR表现为弱降水逐渐降低，中等强度及强降水逐渐上升。同时，不同降水强度各指标下降和上升最快的区间有一定的差异，弱降水均表现为20～30 dBz 上升/下降较快；中等强度及强降水，除中等强度FAR在20～30 dBz 上升较快外，其他指标均表现为30～40 dBz上升/下降较快。

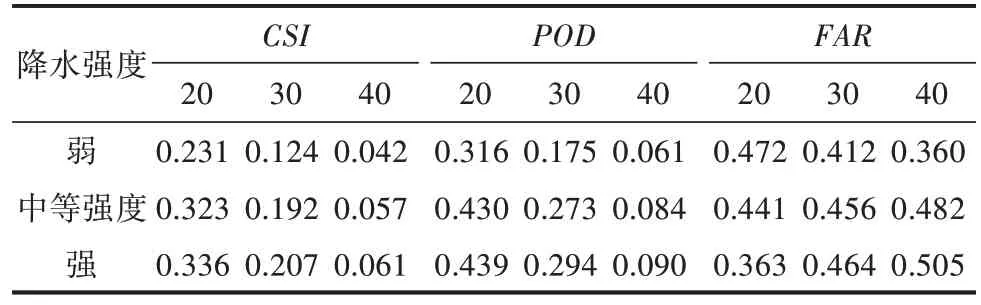
表4 不同降水强度下各阈值回波预报的平均评分

逐个指标来看，除FAR在弱降水≥30 dBz、≥40 dBz 强度上表现最优外，在各强度上（≥20 dBz、≥30 dBz、≥40 dBz）CSI、POD、FAR均表现为强降水最佳。各阈值回波预报中（除≥30 dBz、≥40 dBzFAR以外），强降水与弱降水相比，CSI提升幅度为45.7%～67.1%，POD为38.9%～68.1%，FAR为23.1%。

3.2.2 不同降水性质的检验评估 分别计算各检验指标分散性和区域性2 种降水类型（表5），可以看到与不同降水强度结果类似，POD、FAR、CSI均表现为区域性优于分散性，提高幅度分别为18.2%、18.7%、24.7%。

表5 不同降水性质VET 算法评分

从各评分指标随时间的演变来看，各指标值整体趋势与上述规律一致，都表现出FAR 的缓慢上升以及POD、CSI的缓慢下降。同时，随着时间的推移，FAR之间的差距均表现出逐渐增大的趋势。预报时效 120 min 以内，POD、FAR、CSI均表现为区域性更优，与分散性相比，POD提升幅度为4.3%～26.1%，FAR为15.2%～22.7%，CSI 为7.6%～40.9%。同样进行了不同阈值回波的检验（表6）。整体来看，随着回波强度的增加，CSI和POD都迅速降低，FAR 逐渐上升。同时，不同降水强度各指标下降和上升最快的区间有一定的差异，CSI和POD在30～40 dBz 下降最快，区域性降水FAR在 20～30 dBz 上升最快，而分散性降水在30～40 dBz下降最快。

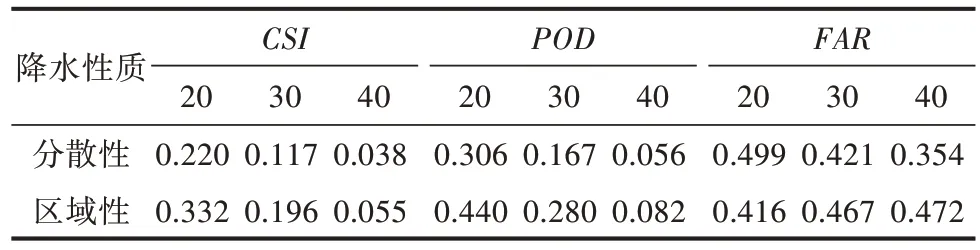
表6 不同降水性质下各阈值回波预报的平均评分

逐个指标来看，除FAR在分散性降水≥30 dBz、≥40 dBz 强度上表现最优外，在各强度上（≥20 dBz、≥30 dBz、≥40 dBz）CSI、POD、FAR均表现为区域性降水最佳。各阈值回波预报中（除≥30 dBz、≥40 dBzFAR以外），区域性较分散性提升幅度分别为45.0%～67.7%、43.8%～67.6%、16.6%。

3.3 案例分析

3.3.1 2021年5月15日7：00—9：00区域性降水 2021年5 月15 日受高空低槽和中低层切变线共同影响，武汉普降大到暴雨，局部大暴雨，全市63%的站点达到暴雨量级，最大小时雨强为58 mm，为典型的区域性强降水。7：00 雷达回波上显示（图3），武汉西北部地区有中心强度超过45 dBz 呈东北-西南走向的带状回波存在，带状回波后侧还伴随有强度稍弱的片状降水回波，从后期回波的演变来看，该带状回波缓慢东移，并略有南压，强度基本不变，但强回波范围有所减小。从VET 的预报来看，120 min 以内，对于回波东移预报较好，回波强度与实况基本吻合，强回波后侧片状回波的发展移动也有所体现，但对于回波的南压预报欠佳。

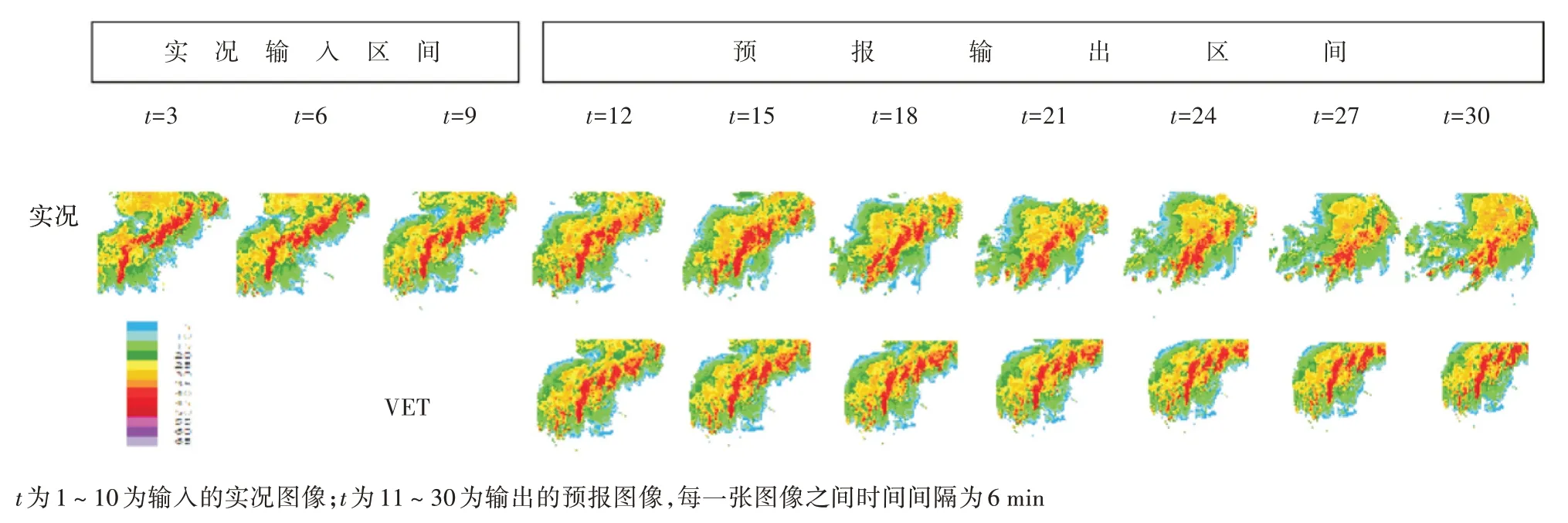
图3 2021 年 5 月 15 日 07：00—09：00 雷达实况和预报对比

3.3.2 2021年9月3日18：00-20：00分散性降水 2021年9 月3 日受低层扰动影响，傍晚至夜间武汉中部出现分散性雷阵雨，局部伴有雷暴大风，降水分布不均，全市平均雨量6 min，最大累计雨量38 min，最大小时雨强 32 min。17：00—18：00 的雷达回波上显示（图4），武汉东北部、南部各有分散性回波存在，回波强度超过50 dBz，但范围均较小，南部回波面积稍大。从回波的演变来看，预报时效内北部回波逐渐减弱消散，移动不大，南部回波自西南向东北方向移动，强度均呈减弱趋势，至19：24 多个分散回波合并后，移动变慢，强度减弱。模式算法的预报结果为对北部回波的预报范围强度均较好，南部回波的移动较实况吻合，仅范围较实况偏弱。120 min内，VET算法对该次分散性回波的发展和移动预报较好。

图4 2021 年 9 月 3 日 18：00—20：00 雷达实况和预报对比

对比分散性和区域性降水的分析结果，VET 机器学习算法不仅对回波运动有一定的把握能力，而且对回波强度的变化也有一定的预报能力，但随着预报时长的延长，预报性能均有所下降，因算法所采用的网络结构在提取空间特征的过程中不可避免的存在信息损失，预报时效越长，信息损失越明显，从而导致预报能力下降。

4 结论

1）从时间演变来看，随着预报时效的延长，VET算法的预报能力逐步下降，表现为FAR缓慢上升以及POD、CSI缓慢下降，但降幅和增幅都随时间逐渐变小，48 min 后曲线变得非常平缓，不同降水性质之间的差异却逐渐增大，且这种差异在一般强度回波时表现得更加显著。

2）随着回波强度的增加，VET 算法的预报能力降低，但其对较强回波的敏感性要强于弱回波，表现为CSI和POD在30～40 dBz下降快于 20～30 dBz。

3）不同降水强度检验来看，VET 算法对于强降水的预报能力优于弱降水；时间演变特征类似，均为强降水更优；不同阈值检验强降水提升幅度均在12%以上，表现出VET 算法对较强回波的预报能力较好。

4）不同降水性质的检验结果类似，分散性和区域性降水各指标不同阈值提升幅度在8.2%～19.7%。

5）对区域性、分散性降水案例的分析结果表明，VET 算法不仅对回波运动有一定的把握能力，而且对回波强度的变化也有一定的预报能力。但随着预报时长的延长，预报性能均有所下降，原因为算法所采用的网络结构在提取空间特征的过程中不可避免的存在信息损失，预报时效越长，信息损失得越明显，从而导致预报能力下降。