滚动转子式压缩机基频振动测试和仿真

李政 王海军

上海海立电器有限公司 上海 201206

0 引言

空调外机配管系统的振动和噪声问题一直是空调和压缩机厂家共同关注的关键问题之一。其中低频振动、噪声极易通过墙体传入室内侧，影响消费者的使用体验。季振勤等通过对空调外机钣金件结构的低频振动和异常噪声的FFT分析，确认了压缩机振动是导致室外机产生低频振动和异常噪声的主要原因[1-3]。因此，准确的预估压缩机的低频振动特性成了亟待解决的关键问题。

长期以来，对压缩机的低频振动的研究主要关注基频回转振动，即滚动转子式压缩机吸排气腔的阻力矩的周期性波动，迫使压缩机产生的往复回转运动[4]，而对压缩机的径向振动和轴向振动关注较少。压缩机回转振动是影响空调配管振动、应力的主要因素，但随着空调配管振动、应力仿真要求的不断提高，仅用回转运动描述压缩机的振动，已经不能满足仿真精度的需求。压缩机径向振动和轴向振动对配管振动、应力的影响逐步凸显。因此，精确模拟压缩机的实际运行状态，是提高空调配管振动、应力仿真准确性的必然要求。

本文以某型号压缩机为研究对象，通过对压缩机壳体表面的工作振型（ODS）测试，获得了压缩机壳体表面的径向、轴向、切向基频振动分布。并通过构建包含内部结构的压缩机模型，分区域进行简谐激励加载，实现了压缩机单体基频振动的精确仿真，并预测了不同压缩机方案的振动变化趋势，最终有效降低了压缩机各方向的基频振动值。

1 压缩机表面振动试验测试

ODS测试是工作状态下结构的两点或多点之间的相对振动。压缩机壳体表面的ODS分析方法，可以获得压缩机在常用工作条件及一定频率下的实际动态特性，可以更加形象、直观地显示压缩机的振动形态[5]。

压缩机壳体表面的工作阵型测试是根据压缩机的壳体形状，将壳体圆柱面分为上中下三层，每层间隔45°设定一个测点（排除储液器连接位置）。用壳体表面共计21个测点来表征压缩机的振动形态，压缩机的测点确定及划分如图1所示。

图1 压缩机壳体表面的ODS测点布置

压缩机运行新国标工况，测得壳体表面的基频振动特性如图2所示，其中压缩机壳体表面振动以回转切向（Y向）振动为主，同时兼有径向（X向）和轴向（Z向）的往复振动。图3是将各测点的切向、径向、轴向基频振动幅值分别提取绘制的壳体振动分布雷达图。其中，0°位置为储液器连接位置（无测点）。表1～表3为壳体各点位置沿三个方向的相位测试结果。

表1 压缩机壳体21点，切向振动相位（°）

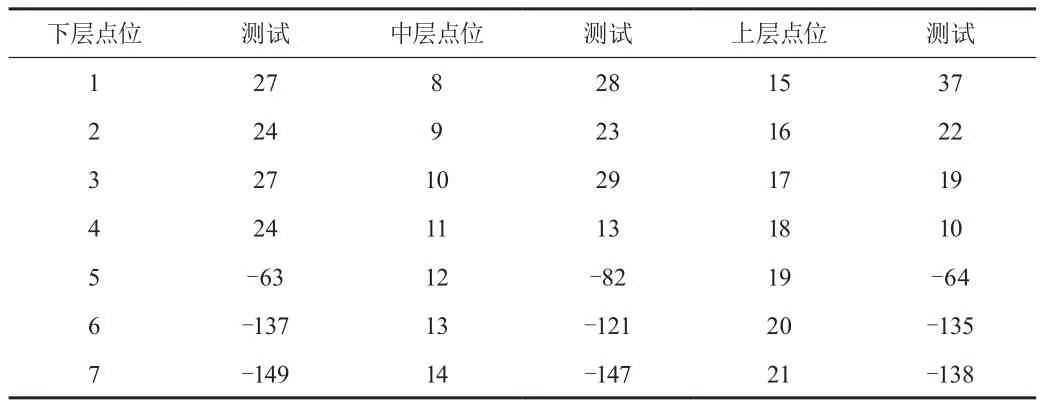
表3 压缩机壳体21点，轴向振动相位（°）

图2 压缩机壳体表面的ODS振型

图3 压缩机振动测试，不同位置的振动分布（m/s²）

由上述压缩机壳体表面不同位置切向、径向和轴向的振动分布结果可知：

（1）压缩机不同点位置的振动值各不相同。压缩机振动以回转切向振动为主，径向振动次之，轴向振动最小。

表2 压缩机壳体21点，径向振动相位（°）

（2）压缩机壳体切向振动：压缩机整体切向振动图形向背离储液器侧偏移；轴向各层沿圆周方向的振动值分布近似圆形；上、下层的切向振动圆心偏移方向相反；各点位置切向振动相位相近同时达到最大振动幅值。

（3）压缩机壳体径向振动：各层振动幅值在圆周方向呈狭长状分布；上、下两端振动幅值大，中间位置振动幅值小。

（4）压缩机壳体轴向振动：相同高度位置，沿圆周方向各点振动幅值不同；相同角度位置，沿轴线方向各点振动幅值及相位基本一致。

2 简谐激励下的强迫振动理论

压缩机运转状态下的载荷激励主要分为电机驱动力矩和气体阻力矩的周期性波动，以及运动部件的惯性力产生的周期性载荷。相对压缩机质心而言，压缩机的总载荷是连续变化的。其大小和方向都在随曲轴转角而动态变化，直接分析非常困难。但是在压缩机的某单一自由度方向上，各载荷的分量具有简谐性或周期性，该方向上的压缩机振动响应符合强迫振动理论。再利用线性系统的叠加原理，将各个分载荷的振动响应叠加，即可获得压缩机在该自由度方向上的总振动响应。

单自由度线性系统的强迫振动的运动微分方程为[6]：

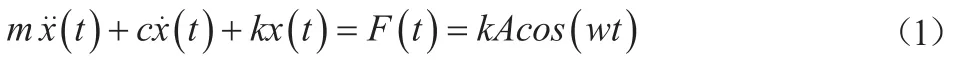
其中，F(t)为谐波激励力；A=F/k是与简谐激励力的力幅F相等的恒力作用在系统上所引起的静位移；k为系统的静刚度。

式（1）微分方程的稳态解为：

其中：X为系统响应的幅值；φ为系统响应的相位。

其中，wn为系统的固有频率；ξ为系统阻尼率。

3 压缩机振动仿真

ANSYS谐响应仿真模块主要分析结构在周期性简谐载荷作用下的动态响应，适用于压缩机基频振动的仿真模拟。压缩机基频振动谐响应计算：首先，建立准确的压缩机三维模型，如图4所示，包括压缩机内部不平衡质量部件、叶片滑动部件和泵体波动力矩承载部件。其次，对压缩机内部各周期载荷进行傅立叶分解，取基频分量作为载荷幅值。并假定压缩机轴系由某一固定点位起始旋转，建立各载荷间的相位关系，模拟压缩机内部激励载荷的作用顺序。其中，回转离心力由两个正交方向的等幅值、相位差90°的载荷组等效。最后，约束压缩机橡胶底脚支撑面，将吸排气管口的连接端做自由边界处理进行模拟仿真。压缩机振动仿真载荷如表4所示。

图4 包含内部结构的压缩机仿真模型

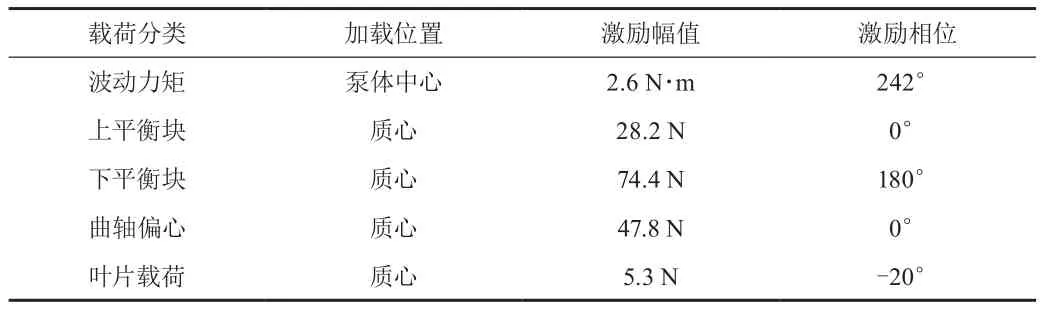
表4 压缩机振动仿真载荷

参考ODS试验壳体测试采样点分布，将壳体表面分为上、中、下三层，每层间隔45°分别提取各点的Y切向、X径向和Z轴向的振动加速度。利用各点位置的振动幅值绘制雷达图如图5所示，统计各点位置在三个方向的相位信息如表5～表7所示。

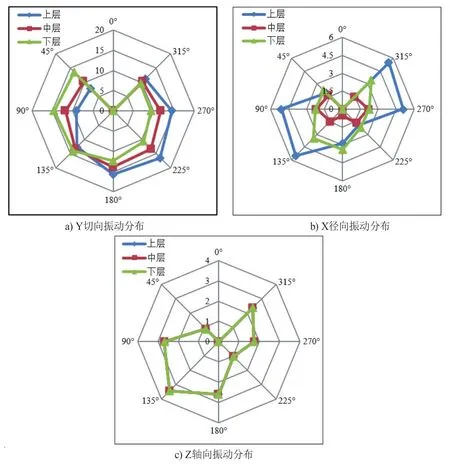
图5 压缩机振动仿真，壳体不同位置的振动分布（m/s²）

对比图3和图5壳体各点位置试验与仿真结果的振动幅值雷达图，以及表5～表7各点位置的振动相位对比可知：压缩机壳体表面振动加速度的仿真结果与试验测试结果分布相近。即压缩机的实际振动表现符合简谐激励下的强迫振动理论，利用ANSYS谐响应仿真模块可以仿真压缩机的切向、径向、轴向振动分布状态。并且仿真方法可以规避多种不必要的试验测试误差，对壳体各点位置的振动分布规律表现的更为清晰。压缩机壳体基频振动分布还有如下特性：

表5 压缩机壳体21点，切向振动的相位对比（°）

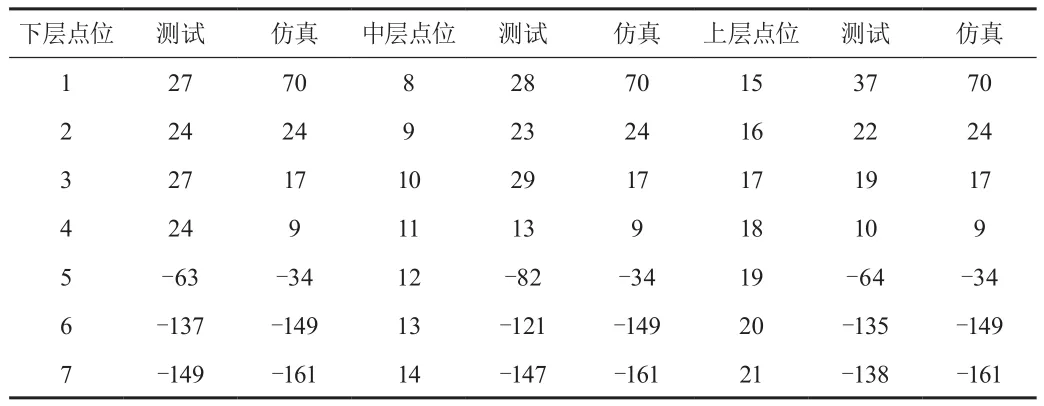
表7 压缩机壳体21点，轴向振动的相位对比（°）

（1）压缩机壳体切向振动：在轴向相同高度处，圆周方向两点间隔180°切向振动幅值相加约等于切向振动均值；

（2）压缩机壳体径向振动：在轴向相同高度处，圆周方向两点间隔180°径向振动幅值基本相同，相位相差180°；

（3）压缩机壳体轴向振动：沿圆周方向，轴向不同高度各点振动幅值与相位均一致。

4 压缩机振动改善

随着空调器厂家对低频振动要求愈加严格，某空调器厂家要求压缩机切向基频主振动小于15 m/s²。实测样机壳体表面最大切向振动幅值为18.3 m/s²，超过样机匹配的振动标准。为降低压缩机的振动值，利用上述仿真模拟方法对三种压缩机变更方案进行模拟仿真和试验测试。对比模拟仿真和试验测试结果，记录壳体表面各测点在三个方向的最大振动加速度，如图6所示。

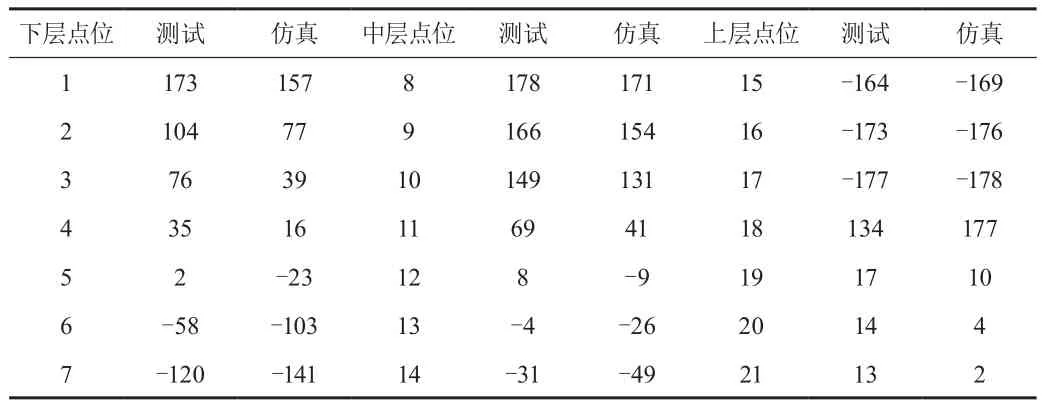
表6 压缩机壳体21点，径向振动的相位对比（°）

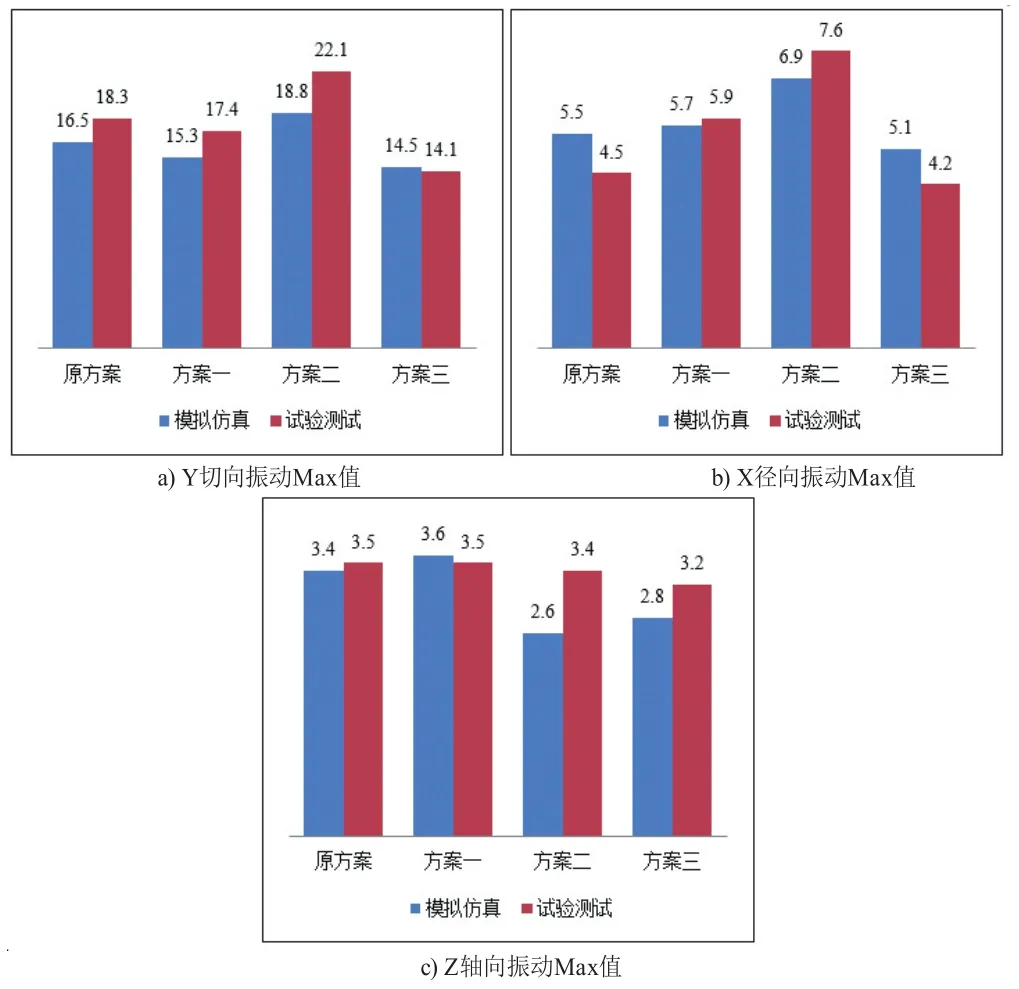
图6 压缩机振动加速度Max值对比（m/s²）

由上述压缩机壳体表面三个方向的振动加速度Max值对比可知：

（1）压缩机振动模拟仿真结果与试验测试结果变化趋势相一致，利用该仿真方法可以准确预测不同方案压缩机的振动改善效果。其中，单向振动最大偏差不大于23%，各方向平均偏差小于12%。

（2）方案一，增加了压缩机切向回转的转动惯量，压缩机切向振动幅值减小，但径向和轴向振动幅值均有增大。

（3）方案二，转子平衡百分比的变更，Y切向和X径向振动幅值均显著变差。

（4）方案三，即增加了压缩机切向回转的转动惯量，同时又调整了压缩机质心位置和回转轴线的倾斜程度。压缩机壳体表面三个方向的振动幅值均有改善，切向振动降低23%，径向振动降低6%，轴向振动降低8%，满足空调器厂家切向振动小于15 m/s²的要求。

5 结论

本文通过ODS方法测试了压缩机运行状态下的壳体振动分布规律，并利用谐响应仿真方法准确的模拟了压缩机的基频振动。根据试验测试和模拟仿真的结果表明：

（1）压缩机壳体表面不同点位置的振动值各不相同。压缩机振动以回转切向振动为主，径向振动次之，轴向振动最小。

（2）压缩机壳体切向振动：压缩机整体切向振动图形向背离储液器侧偏移；轴向各层沿圆周方向的振动值分布近似圆形；上、下层的切向振动圆心偏移方向相反；各点位置切向振动相位相近同时达到最大振动幅值。在轴向相同高度处，圆周方向两点间隔180°切向振动值相加，近似等于切向振动均值；

（3）压缩机壳体径向振动：各层振动幅值在圆周方向呈狭长状分布；上、下两端径向振动幅值大，中间位置振动幅值小；轴向相同高度位置，在圆周方向两点间隔180°时，径向振幅基本相同，相位相差180°；

（4）压缩机壳体轴向振动：相同高度位置，沿圆周方向各点振动幅值不同；相同角度位置，沿轴线方向各点振动幅值与相位均一致。

（5）压缩机振动模拟仿真结果与试验测试结果变化趋势相一致，利用该仿真方法可以准确预测不同方案压缩机的振动改善效果。其中，单方向振动最大偏差不大于23%，各方向平均偏差小于12%。

（6）增加转动惯量调整质心位置，可以有效降低压缩机三个方向的振动值。本次试验结果，压缩机壳体表面切向振动降低23%，径向振动降低6%，轴向振动降低8%。