大跨径钢筋混凝土拱桥拱肋斜拉扣挂施工扣索索力计算与优化

谌 呈

(怀化市农村公路建设办公室， 湖南 怀化 418000)

0 前言

大跨度钢筋混凝土拱桥预制拱肋采用斜拉扣挂法吊装施工时，扣索索力计算是其中的一大难点，确保预制拱肋节段在吊装过程中截面上下缘拉压应力不超标以及拱肋节段合龙后线形与一次落架成拱线形一致是斜拉扣挂法扣索索力计算控制重点。对于斜拉扣挂法合理扣索索力的计算，大量从业人员研究了许多实用方法，如零位移法、零弯矩法、力矩平衡法以及弹性-刚性支撑法等[1]，研究方向的偏重点不同导致各种方法各有利弊。本文以改进零位移法和弹性-刚性支撑法对工程实例进行扣索索力计算，通过对比扣索索力大小和预制拱肋节段各施工阶段截面上下缘最大拉压应力的大小，挑选较为合理的一组索力，同时分析两种方法利与弊。最后运用未知荷载系数法对该组索力进行优化分析，使拱肋施工阶段应力与合龙成拱后线形更加出色，从而达到预定的控制要点，满足实际施工要求。

1 计算理论

1.1 改进零位移法

零位移法基本原理为：以拱肋索扣点处的位移为零作为控制目标，通过调整索力大小，使索力与拱肋节段自重达到平衡，此时拱肋上索扣点均达到设计拱轴线的标高[2]。运用有限元计算时，通常将扣索模拟为位移为零的刚性支座，通过求解支座的X方向与Y方向的支座反力，来求解两个方向的合力作为扣索的索力。

(1)

式中：Ti为各根扣索索力；Fxi为支座处水平反力；Fyi为支座处竖直反力。

然而，零位移法计算过程中很难确保支点反力的合力方向与扣索的张拉方向一致，索力有可能出现负值[3]。因此，需对零位移法进行改进，即沿着各根扣索张拉方向逐根添加链杆约束，此约束提供的反力方向必定与设计拱肋轴线状态下的扣索力方向一致[4]。

1.2 弹性-刚性支撑法[5]

基于弹性-刚性支撑法解析法的研究思路，通过Midas软件有限元法求解扣索索力。

1)采用斜拉扣挂法安装第1段拱肋节段时，将扣索轴向刚度设定为无穷大(将刚度参数改为100000倍)来计算此时1#扣索初拉力T1，1和1#索扣点竖向位移Δ1，1，如图1所示。

2)安装第2段拱肋节段时，将1#扣索轴向刚度改为正常值，2#扣索轴向刚度增加100000倍，计算此时2#扣索初拉力T2，2、1#扣索索力增量ΔT1，2、1#索扣点竖向位移Δ1，2和2#索扣点竖向位移Δ2，2，如图2所示。

3)同样安装第3段拱肋节段时，将1#、2#扣索轴向刚度调整为正常值，3#扣索轴向刚度增加100000倍，计算此时3#扣索初拉力T3，3和1#、2#扣索索力增量ΔT1，3、ΔT2，3以及1#、2#、3#索扣点竖向位移Δ1，3、Δ2，3、Δ3，3。

4)以此类推逐段安装拱肋，计算扣索初拉力、索力增量以及扣点竖向位移，直至合龙。按此思路，得到各扣索初拉力和索力增量，合龙后的扣索最终索力为该根扣索初拉力与各个安装阶段该根扣索索力增量之和，即：

(2)

式中：Ti为第i根扣索最终索力；Ti，i为第i根扣索初拉力；ΔTi，j为第i根扣索在第j阶段的索力增量。

各拱肋节段预抬量为各个安装阶段各索扣点竖向位移之和，即：

(3)

式中： Δi为第i拱肋节段预抬量；Δi，i为安装第i拱肋节段时第i号索扣点竖向位移；Δi，j为安装第j拱肋节段时第i号索扣点竖向位移。

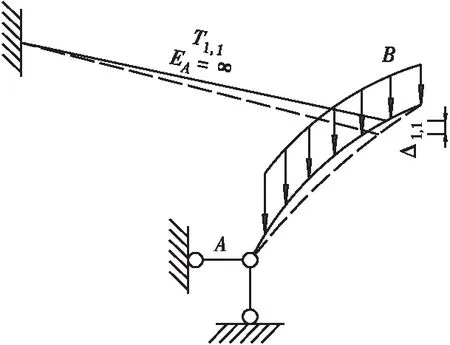
图1 第1节段安装就位示意

图2 第2节段安装就位示意

1.3 未知荷载系数法[6]

未知荷载系数法的原理是通过设置拱桥拱肋安装过程中的约束条件，求出满足约束条件的合理变量值，它的理论基础是影响矩阵法[7-8]。

大跨度钢筋混凝土拱桥斜拉扣挂法施工过程中需要控制的重点如下： ①预制拱肋节段截面拉压应力不超标(拉应力≤1.83 MPa，压应力≤22.4 MPa)；②合龙后线形基本与一次落架拱肋线形一致[9-10]。明确控制目标，可建立以下索力优化模型，优化公式如下所示。

F=Ku

(4)

式中：F为荷载产生的等效力向量；K为整理刚度矩阵；u为位移向量。

(5)

上述索力优化模型表明：在满足索扣点竖向位移和拱肋节段截面应力不超限制值的条件下，目标值为最小值时的索力为最优索力。

2 工程实例

2.1 工程概况

牛路河特大桥是一座全长430.08 m的钢筋混凝土拱桥，结构为上承式，主拱圈截面为单箱双室截面，标准截面尺寸为高360 cm，宽780 cm；主孔技术参数:净跨径195 m，净矢高39 m，净矢跨比1/5，拱轴系数1.543。主拱圈平面、立面和标准截面如图3、图4所示。

2.2 主拱圈吊装施工节段划分与工况描述

主拱圈分为42个预制节段、2个现浇段、6处湿接缝和1个合龙段，主拱圈沿中轴线对称分布，所以采用对称斜拉扣挂吊装施工，两岸相对应的拱肋节段编号一致。主拱圈采用无支架缆索吊装斜拉扣挂法施工，拱肋安装施工顺序为： ①设置临时支架，安装主拱圈两岸第1节拱箱，拱脚采用铰接形式；②安装第2节拱箱，调整标高后扣定扣索KS2；③安装第3节拱箱，调整标高后扣定扣索KS3，拆除1#节段下方临时支架；④继续安装第4、5节拱箱，调整标高后扣定对应扣索KS4、KS5；⑤安装第6节拱箱，调整标高后扣定扣索KS6，同时固结拱脚，改变结构体系；⑥继续安装剩余拱箱节段直至拆索合龙。

图3 1/2主拱拱圈分段立面与标准截面(单位： cm)

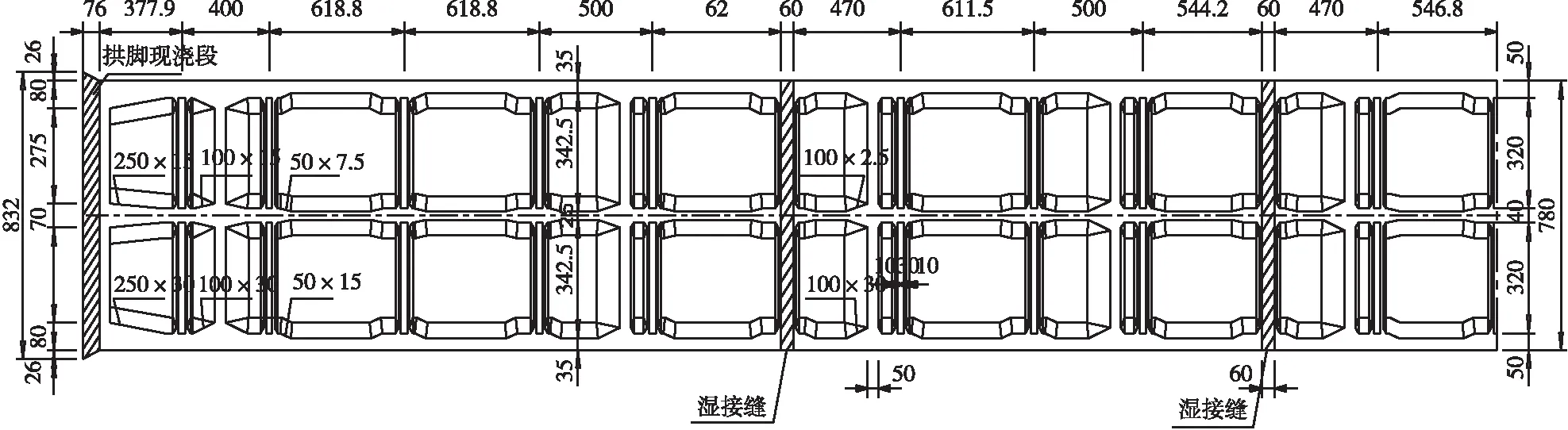
图4 部分主拱圈平面(单位： cm)

2.3 有限元模型建立

本算例采用有限元软件Midas Civil 2015进行建模分析，因为索力计算方法的不同，分别建立两种模型进行模拟计算。改进零位移法模型包含538个节点和538个单元，主拱圈采用梁单元模拟，链杆单元采用桁架单元模拟，模型考虑预拱度影响，节点边界条件根据改进零位移法原理进行设定(即约束索扣点X方向与Y方向竖向位移)。弹性-刚性支撑法模型包含558个节点和578个单元，主拱圈采用梁单元模拟(共498个梁单元)，扣索采用桁架单元模拟(共80个桁架单元)，运用等效面积进行模拟，拱脚边界条件采用先铰接后固结(根据施工顺序，在扣定KS6扣索时进行体系转换)。具体模型建立如图5、图6所示。

图5 有限元模型(改进零位移法)

图6 有限元模型(弹性-刚性支撑法)

2.4 传统扣索索力计算方法结果对比分析

采用Midas Civil 2015基于改进零位移法与弹性-刚性支撑法进行扣索索力计算，两种索力计算方法的初拉力值如表1所示。

根据表1改进零位移法与弹性-刚性支撑法计算的扣索索力计算值，将其分别代入模型进行正装分析，得出施工阶段拱圈关键截面上下缘拉、压应力值(见表2)。

表2所示的应力值，正值代表拉应力，负值代表压应力。为了便于分析两种方法下拱肋截面应力值的变化规律以及计算结果差异性，绘制两种方法下的各施工阶段截面最大拉压应力对比如图7、图8所示。

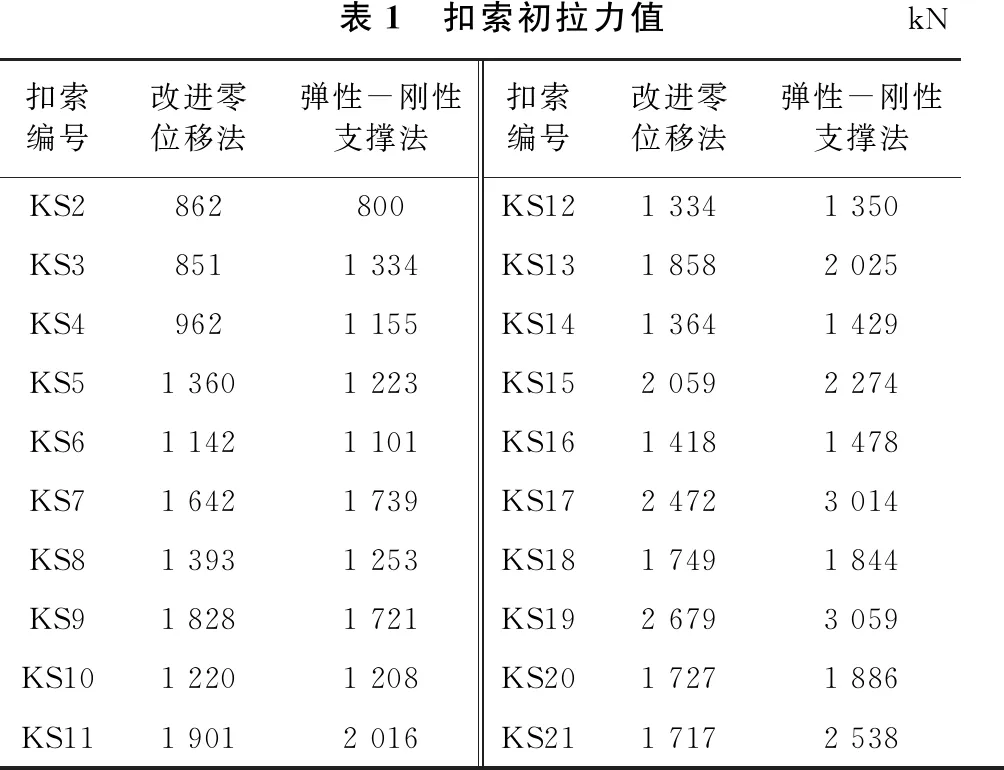
表1 扣索初拉力值kN扣索编号改进零位移法弹性-刚性支撑法扣索编号改进零位移法弹性-刚性支撑法KS2862800KS121 3341 350KS38511 334KS131 8582 025KS49621 155KS141 3641 429KS51 3601 223KS152 0592 274KS61 1421 101KS161 4181 478KS71 6421 739KS172 4723 014KS81 3931 253KS181 7491 844KS91 8281 721KS192 6793 059KS101 2201 208KS201 7271 886KS111 9012 016KS211 7172 538

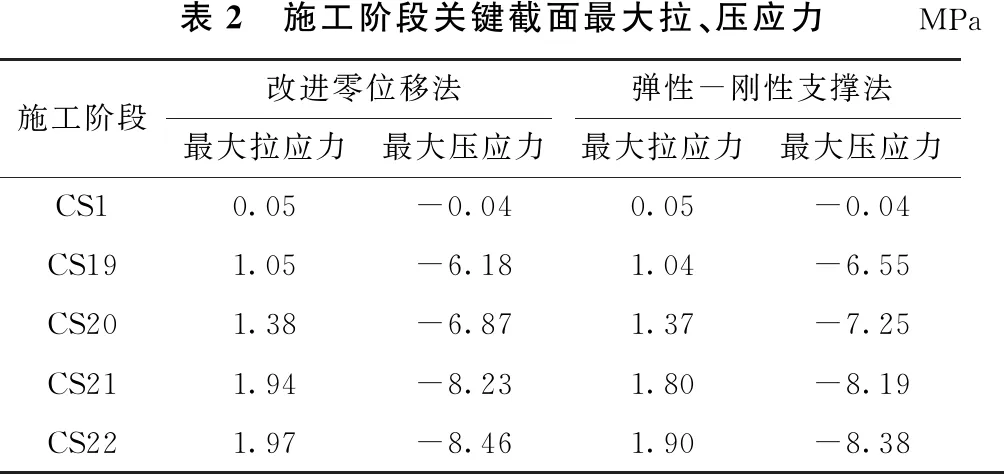
表2 施工阶段关键截面最大拉、压应力MPa施工阶段改进零位移法弹性-刚性支撑法最大拉应力最大压应力最大拉应力最大压应力CS10.05 -0.04 0.05 -0.04 CS191.05 -6.18 1.04 -6.55 CS201.38 -6.87 1.37 -7.25 CS211.94 -8.23 1.80 -8.19 CS221.97 -8.46 1.90 -8.38

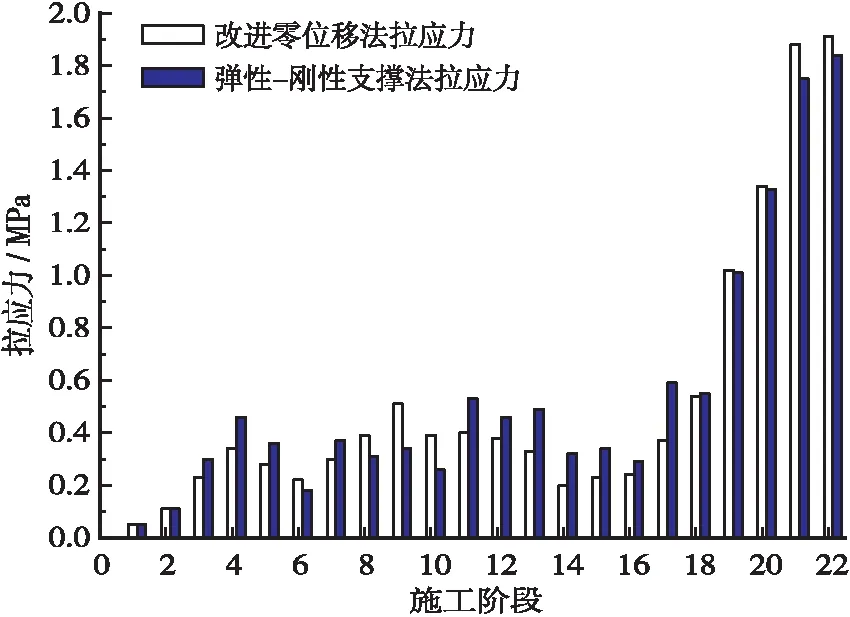
图7 各施工阶段截面最大拉应力对比

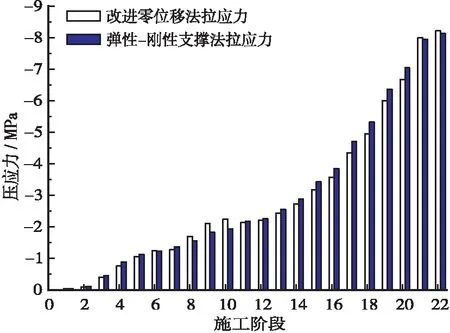
图8 各施工阶段截面最大压应力对比

根据表2以及图7、图8可知，基于改进零位移法下拱肋各施工阶段最大拉应力出现在SC22阶段，最大值为1.97 MPa，最大压应力也出现在SC22阶段，最大值为8.46 MPa；基于弹性-刚性支撑法下拱肋各施工阶段最大拉应力出现在SC22阶段，最大值为1.90 MPa，最大压应力也出现在SC22阶段，最大值为8.36 MPa。对比分析，可以得出3个结论： ①通过两种方法计算得出的应力变化趋势基本相同，且拉压应力基本相差不大；②采用弹性-刚性支撑法计算的应力结果比改进零位移法计算的应力结果表现要优秀；③主拱圈采用C50混凝土，按照规范规定的设计值，截面应力控制目标为最大拉应力≤1.83 MPa，最大压应力≤22.4 MPa，两种方法计算的施工阶段最大拉应力分别为1.97 MPa和1.90 MPa，因此不能达到预定的控制目标，需要对扣索索力进行优化。

2.5 扣索索力优化计算

运用Midas有限元软件中未知荷载系数法功能，采用基于弹性-刚性支撑法的优化方法对扣索索力进行优化分析。施工计算方法依旧采用正装分析。控制目标为：①预制拱肋节段截面拉压应力不超标(拉应力≤1.83 MPa，压应力≤22.4 MPa)；②合龙后线形基本与一次落架拱肋线形一致(扣索扣点位移不超过限定值)。具体优化结果如表3所示。

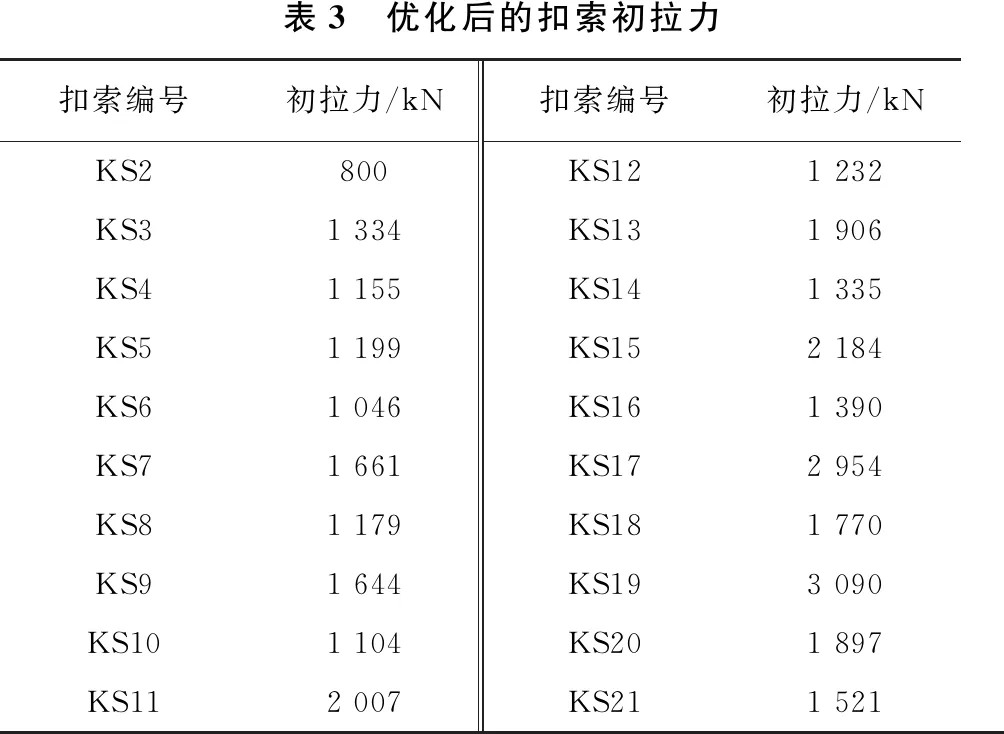
表3 优化后的扣索初拉力扣索编号初拉力/kN扣索编号初拉力/kNKS2800KS121 232KS31 334KS131 906KS41 155KS141 335KS51 199KS152 184KS61 046KS161 390KS71 661KS172 954KS81 179KS181 770KS91 644KS193 090KS101 104KS201 897KS112 007KS211 521

将优化后的扣索初拉应力代入模型中进行正装分析，得出优化后的施工阶段关键截面最大拉、压应力(见表4)。

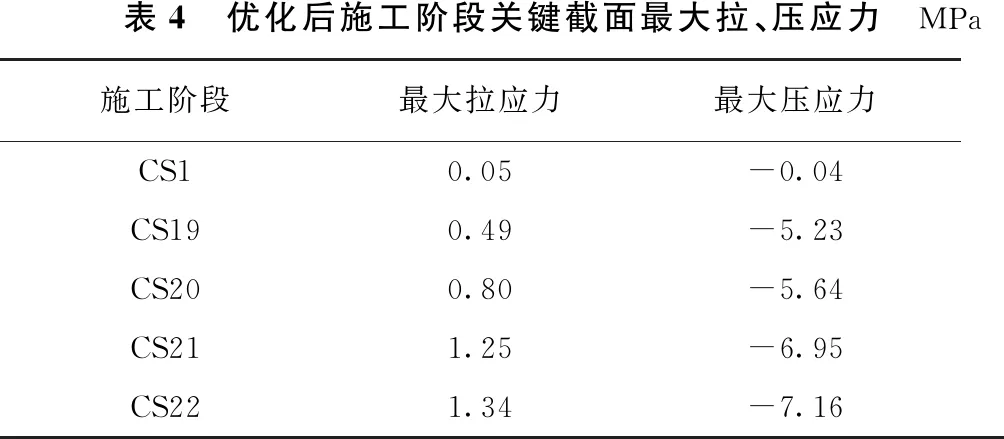
表4 优化后施工阶段关键截面最大拉、压应力MPa施工阶段最大拉应力最大压应力CS10.05-0.04CS190.49-5.23CS200.80-5.64CS211.25-6.95CS221.34-7.16

与优化前的弹性-刚性支撑法计算应力进行对比分析，见图9、图10。

图9 优化前后截面最大拉应力对比

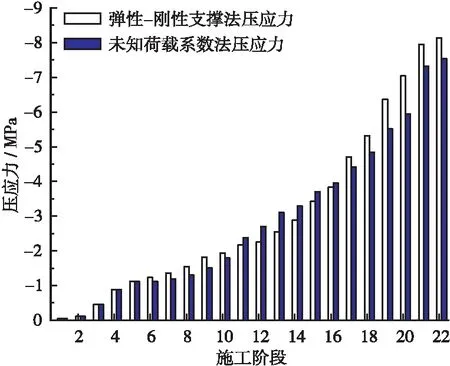
图10 优化前后截面最大压应力对比

由表4以及图9、图10可知，经过优化的各施工阶段截面上下缘最大拉压应力均得到了有效改善，关键截面的拉压应力大幅下降，其中，最大拉应力与最大压应力依旧出现在CS22施工阶段，分别为1.34 MPa(≤1.83 MPa)和7.16 MPa(≤22.4 MPa)，两者均达到预定应力控制目标，在保证安全的情况下满足施工要求。

在线形优化方面，将优化前后的扣索初拉力值代入模型正装计算，得出合龙并拆索成拱后的拱圈线形，并与一次落架成拱后的线形进行对比分析，对比情况如图11所示。

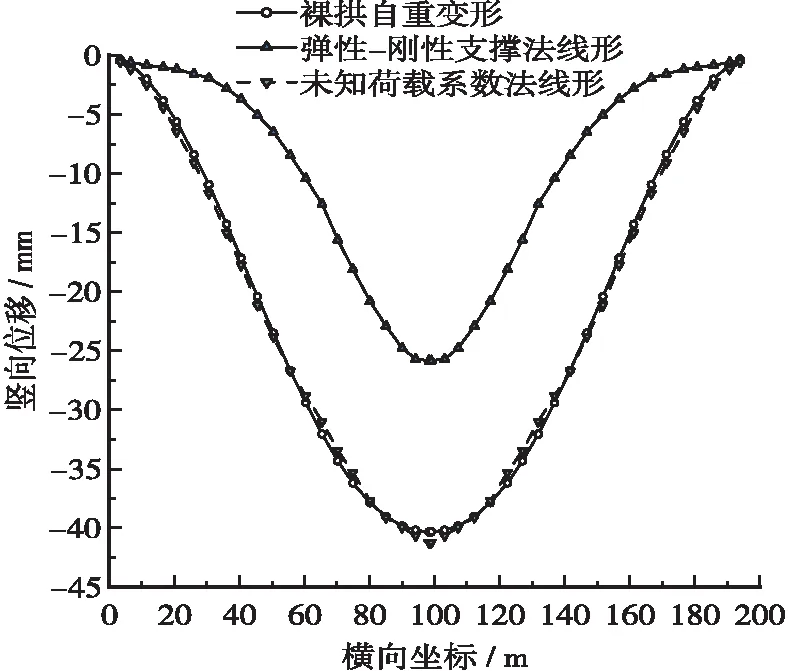
图11 优化前后与一次落架成拱后的线形对比

图11表明：弹性-刚性支撑法计算的扣索初拉力经正装分析后，不仅应力不能满足要求，而且拆索后的成拱线形与一次落架成拱后的线形也有一定偏差，最大偏差值高达21 mm，与设计要求不相符合。而采用未知荷载系数法优化后的线形基本与一次落架成拱线形相符合，最大偏差仅3 mm。因此在成拱线形方面，优化后的索力依旧满足线形控制目标。

3 结论

1) 采用改进零位移法与弹性-刚性支撑法能分别计算得出一组基本扣索初拉力值，通过模拟斜拉扣挂正装分析，这两种方法计算的索力值并不能满足大跨径钢筋混凝土拱桥施工过程中应力与线形控制要求，但对截面应力限定范围偏大的钢管混凝土拱桥来说，这两种传统的扣索索力计算方法具有一定的参考意义。

2) 经两种传统索力计算方法对比分析可知，弹性-刚性支撑法计算结果比改进零位移法更合理、更符合实际施工情况。

3) 运用未知荷载系数法优化的索力不仅能满足主拱圈截面应力控制条件，而且成拱后的线形与一次落架成拱线形相符合，该优化方法对于采用斜拉扣挂体系施工的大跨径钢筋混凝土拱桥正装施工分析具有实操意义，值得推广应用。