定制家具企业订单组批方式对板材利用率的影响

秦晓宇，徐伟,2*，詹先旭

(1. 南京林业大学家居与工业设计学院，南京 210037； 2. 南京林业大学智库林业产业发展中心， 南京 210037；3. 德华兔宝宝装饰新材股份有限公司，浙江 德清 313200)

随着制造技术与管理技术的发展及市场需求的变化与竞争的加剧，定制家具产业逐渐兴起[1]。板式定制家具产业是以大批量生产的速度和成本为客户生产个性化的多品种小批量定制家具的大规模定制产业[2-3]。板式定制家具大多采用“订单组批+按批生产+分拣集成”的揉单生产模式[4]。订单组批是按照一定的规则将一定数量的订单揉合成若干生产批次的过程[5]。按批生产要经过开料、封边、钻孔、分拣等几个重要工段[6]。开料是按照订单中工件的尺寸和花色、厚度等要求将人造板基材(或饰面人造板)裁切成符合要求的毛料的加工过程。现代板式定制家具企业开料一般使用电子开料锯，按照板材排样方案裁切[7]。

板材的利用率定义为订单中的所有工件面积之和与生产订单使用的原料板材面积之比。由于工件的尺寸及原料板材尺寸的限制，排样不能使工件完美的平面镶嵌于整个原料板材，所以开料中必定产生余料废料，板材的利用率不会达到100%。板材成本是板式家具制造企业生产成本的一个重要部分，约占生产成本的40%左右[8]。提高板材的利用率对于降低生产成本、增加企业利润有着重大的价值。

关于提高板材利用率的研究目前主要集中在两个方面：一方面是排样，直接决定了板材的利用率；另一方面是订单的组批。组批并不是随机抽取订单组成批次，而是有不同的方式，如按照主花色、订单交期、来源地址等多种方式，也有通过算法聚类订单的组批方式[9]。对于组批问题的研究目前集中在订单拣选、排序及物流路径的集成优化等方面，也有将组批与排样问题结合协同优化的研究[10-11]。

组批方式与板材利用率密切相关，本研究从统计学的角度，通过对某板式定制家具制造企业两种不同组批方式的两条生产线一段时间内板材利用率数据的统计分析，提出两种不同组批方式下影响板材利用率的主要因素；通过建立回归方程，预测板材利用率；并比较相同订单不同组批方式下板材利用率的差异，为企业综合考虑各方面成本，选择合适的组批方式提供参考。

1 数据来源与统计分析方法

1.1 数据来源

本研究使用的数据来源于A企业，A企业是一家大型板式家具制造企业。A企业使用的开料裁板设备是金田豪迈的卧式板材开料锯SAWTEQ B-300，排样优化使用CutRite V11板材开料优化软件[12]。A企业将衣柜订单分为两类，一类是零售订单，在零售线生产；另一类是样品订单，在样品线生产。

零售线订单采用按照主花色组批的方式。零售单广泛来自全国各地的加盟商，排产时以交付日期为约束，将交付日期一致的订单安排到同一天生产，导致每日生产的数量庞大的订单发货地址各不相同，花色品类也相当繁杂。为了避免批次内订单过多导致产线无法周转，首先限制批次内容纳订单数量，然后规定订单中常见的花色为主花色，识别订单中的主花色，将主花色相同的订单组为一个批次，超过规定数量的订单组到下一批次中，最后将几个订单数量过少的批次揉合为一个批次。

样品线生产的加盟商样品订单采用按照来源地址组批的方式。加盟商样品订单来单比较集中，往往一个地址就可能有10个左右订单，且每单的板块数达到200以上，故可将一地的订单自然成批。如果出现某地订单较少的情况，将两地订单合并组成一批处理。

两条产线采用不同的组批方式，影响板材利用率的主要因素也不相同，本研究连续观测采集一段时间内两条产线的利用率及相关数据，通过Excel和SPSS 25.0软件进行数据处理、统计分析及图表绘制。

1.2 统计分析方法

依据订单组批及排样优化工作的经验，不同组批方式下与板材利用率相关的因素可能有单量、板块数、花色、批次容量等。单量是指参与组批的订单数量；板块数是指参与组批的所有订单的工件总数；花色是指参与组批的所有订单的花色总数(同种花色不同厚度的工件记为不同花色)，即开料所需原料板材种类数；批次容量是指组批完成后，每个批次容纳订单的平均数量，即单量与批次数之比。本研究将单量、板块数、花色、批次容量作为预测变量，板材利用率作为因变量，通过正态性检验、相关性分析、回归分析等统计分析方法，分析预测变量与因变量之间的定性定量关系。

数据符合正态分布是相关性分析和回归分析的前提。本研究首先通过单样本Kolmogorov-Smirnova(KS)检验方法对预测变量及利用率数据进行正态性检验。KS检验的显著性，即P值，如果P>0.05，表示数据符合正态分布；否则数据不符合正态分布。确认数据符合正态分布后，可进行预测变量与利用率之间的相关性分析。

相关性分析用于分析两对或多对变量之间的相关程度，本研究采用Pearson相关分析方法评估预测变量与利用率间的相关性。Pearson相关系数为正值表示两变量间正相关，为负值表示两变量间负相关；绝对值越接近1表示变量间的相关程度越高。

回归分析是确定两种或两种以上变量间定量相关关系的一种统计学方法，可以用于预测因变量的变化[13]。逐步回归是逐一将自变量加入回归模型，直至某个变量的加入使原加入变量不显著时剔除，重复这个过程直至所有显著变量全部加入回归模型。本研究通过逐步回归的方法建立预测板材利用率的回归方程。预测变量间的强相关关系会导致共线性问题，降低回归方程预测的准确性，所以不将有强相关关系的预测变量同时投入模型。

配对样本T检验用于检验配对设计实验中成对定量数据是否有显著差异。本研究用于分析同样的订单数据采取两种不同组批方式所得的利用率是否有显著差异。通过P值判断结果显著性，若P<0.05，表示两种组批方式的利用率有显著差异；若P>0.05， 则表示两种组批方式的利用率没有显著差异。

2 两产线板材利用率数据分析

2.1 零售线板材利用率数据分析

零售线按照主花色组批，采集了66组样本数据。数据显示零售线每日平均有193个订单，总板块数达到9 758块，平均包含花色48个，每个批次平均包含订单22个，板材的平均利用率达79.20%。通过SPSS 25.0软件中的单样本KS检验功能分析数据是否符合正态分布，结果见表1。单量、板块数、花色、批次容量、利用率的P值均大于0.05，故判断单量、板块数、花色、批次容量、利用率均为正态分布数据，可进行相关性分析与回归分析。

表1 零售线数据单样本KS检验Table 1 Single sample KS test of retail production line data

应用SPSS 25.0软件的散点图功能作利用率与单量、板块数、花色、批次容量间的相关关系图(图1)，利用率与单量、板块数、批次容量呈正相关关系，与花色呈负相关关系。

图1 零售线板材利用率与预测变量相关关系Fig. 1 Scatter chart of correlation between boards utilization rate and predictor variables in retail production line

应用SPSS 25.0软件中的双变量相关功能，评估5个变量间的Pearson相关性，结果如表2所示。

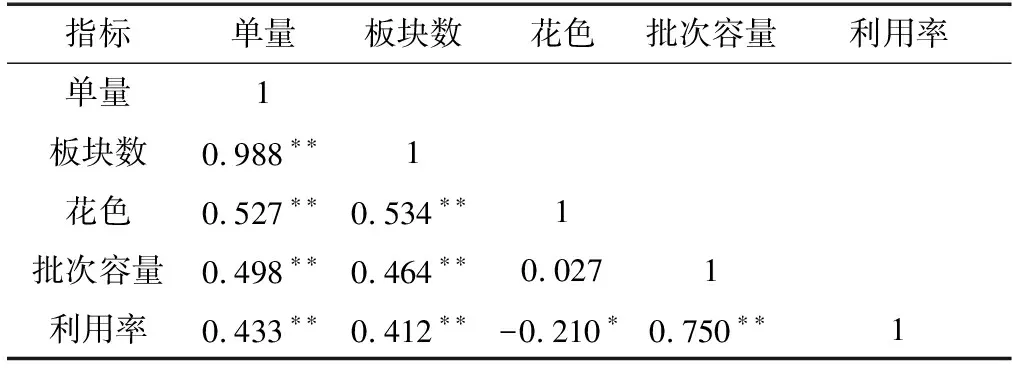
表2 零售线板材利用率与预测变量间的相关性分析Table 2 The correlation analysis between the panels’ utilization rate and the predictor variables in retail production line

利用率与单量、板块数、花色、批次容量间的相关系数分别为0.433，0.412，-0.210，0.750，且均为显著相关。单量与板块数的相关系数达到0.988，是强相关关系，为了避免共线性，在回归分析中单量与板块数不应同时加入回归方程。而单量是比板块数更直观的指标，所以在回归分析中，不加入板块数这一变量。

应用SPSS 25.0软件的线性回归功能作回归分析，选择逐步回归的方法，将利用率作为因变量，单量、花色、批次容量作为自变量，所得的结果见表3。比较调整后R2，模型1<模型2<模型3，可知模型3是最优模型。模型3的预测变量是批次容量、花色、单量，其调整后系数R2=0.664，F=43.899，P<0.001，可以显著地解释因变量利用率的变化。其中批次容量对板材利用率的影响最大，其回归系数为0.361，花色与利用率负相关，回归系数为-0.074，单量的回归系数为0.011。

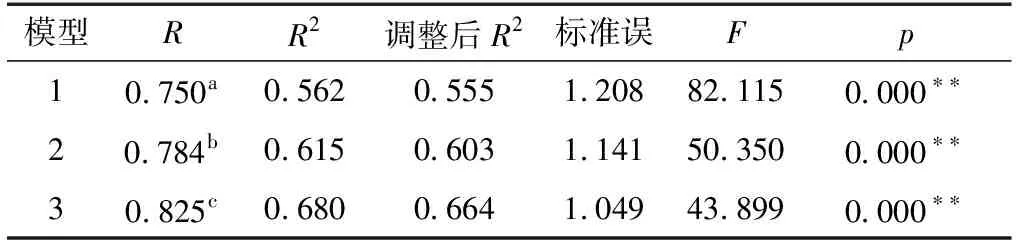
表3 零售线回归模型结果Table 3 Overview of retail production linear regression model results

故影响板材利用率的主要因素依次是批次容量(X1)、花色(X2)、单量(X3)，回归分析所得最优多元线性回归方程为Y=0.361X1-0.074X2+0.011X3+72.762。通过线性回归方程可以直观地预测板材利用率的变化。当批次容量(X1)每增加1单，其他2个变量固定在某一正常取值时，板材利用率预计提高0.361%。同理，当花色(X2)每减少1个、单量(X3)每增加1单时，板材利用率将分别提高0.074%和0.011%。在零售线的实际生产中要尽量增加批次容量和单量，并减少花色种类，以提高板材利用率。

2.2 样品线板材利用率数据分析

样品线按照来源地址组批，采集了58组样本数据。数据显示样品线每日平均有58个订单，总板块数达到4 175块，平均包含花色42个，每个批次平均包含订单13个，板材的平均利用率达72.26%。通过KS检验分析单量、板块数、花色、批次容量、利用率是否符合正态分布，结果如表4所示：花色、批次容量、利用率的P值均大于0.05，符合正态分布；单量、板块数的P值小于0.05，不符合正态分布。

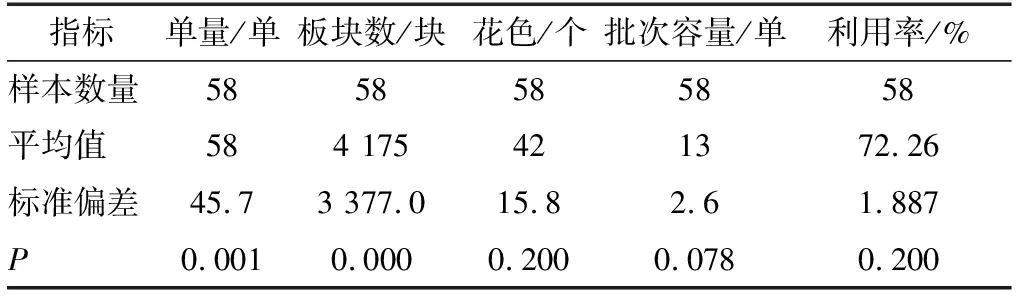
表4 样品线数据单样本KS检验Table 4 Single sample KS test of sample production line data

对数转换不会改变数据的性质和相关关系，所以对单量与板块数做自然对数转换，再次对转换后的数据做KS检验，结果如表5所示，两者的P值均大于0.05，则认为单量和板块数对数转换后符合正态分布。将对数转换后的单量、板块数记为单量*、板块数*。

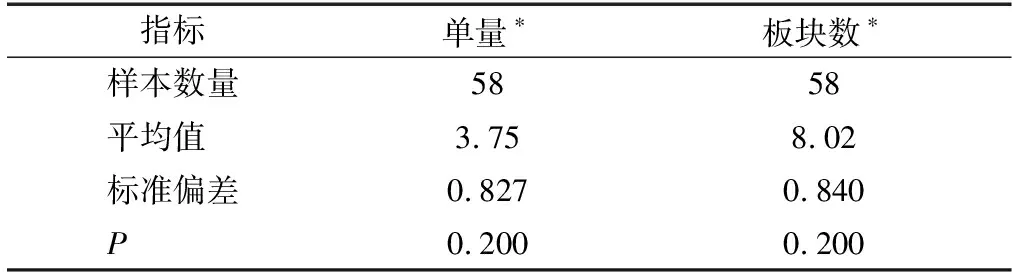
表5 样品线单量、板块数对数转换KS检验Table 5 Single sample KS test of order quantity and panel quantity by log conversion

作利用率与单量*、板块数*、花色、批次容量间的相关关系图如图2所示，利用率与4个变量均为正相关关系。

图2 样品线板材利用率与预测变量相关关系Fig. 2 Scatter chart of correlation between panels’ utilization rate and predictor variables in sample production line

计算5个变量间的Pearson相关系数，结果见表6。利用率与单量*、板块数*、花色、批次容量间的相关系数为0.595，0.621，0.441，0.330，相关性均显著。单量*与板块数*间的相关系数为0.984，单量*与花色间相关系数为0.928，均为强相关关系，导致花色和板块数对利用率的影响几乎与单量一致，而单量是比其他两者更容易获取的指标，因此在利用率回归方程中不加入这两个变量。

表6 样品线板材利用率与预测变量间的相关性分析Table 6 The correlation analysis between the panels’ utilization rate and the predictor variables in sample production line

回归分析中，单量*与批次容量作为预测变量，利用率作为因变量，得到回归模型如表7所示，批次容量在逐步回归中被去除。所得模型的自变量是单量*，因变量是利用率。调整后R2=0.342，F=30.652，P<0.001，表示此回归方程可以显著预测因变量利用率的变化。所以回归分析所得的回归方程为Y=1.356lnX+67.163(X=单量)。从回归方程可知，按来源地址组批方式下，对板材利用率影响最大的因素是单量，单量增加，板材利用率随之提高。

表7 样品线板材利用率回归分析Table 7 Regression analysis of utilization rate of sample production line

2.3 按主花色组批与按来源地址组批数据对比分析

为了直观地比较两种组批方式的板材利用率是否有差异，选取样品线4组订单数据，分别按照两种组批方式排样优化，所得的板材利用率数据如表8所示。按来源地址组批的板材利用率平均值为73.93%，按主花色组批的板材利用率平均值为79.78%。

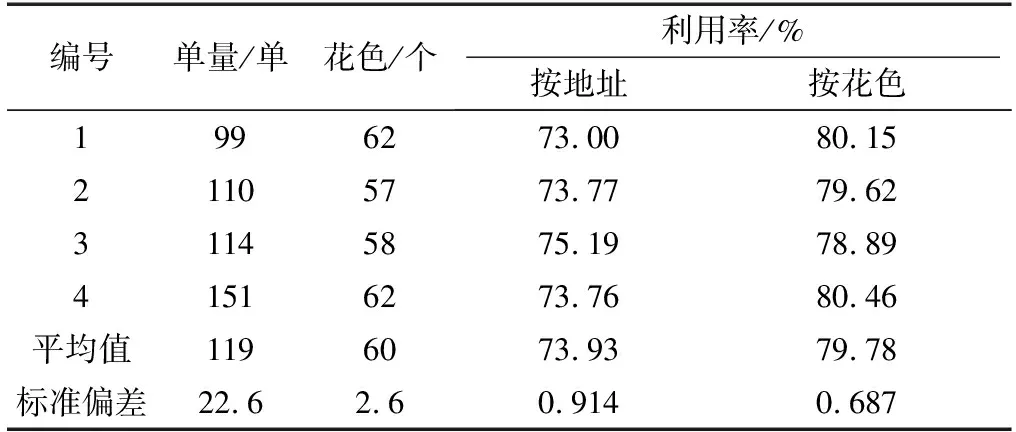
表8 两种组批方式数据统计Table 8 Data statistics of two group batch rules

由于两组数据是相同订单采用不同组批方式所得，所以使用配对样本T检验分析是否有显著差异，计算可知，标准偏差为1.531，t=-7.64，P=0.005<0.01，表示按来源地址组批与按主花色组批的板材利用率有极显著差异，且按主花色组批的板材利用率显著高于按来源地址组批。

虽然对于样品订单，按主花色组批的板材利用率高于按来源地址组批，但是在实际生产中，样品订单生产齐套后还有齐户组装(某来源地址所有订单生产齐套后，一同组装以检验整体效果)的工序。按来源地址组批，则在批次生产完成后自然齐户，可直接组装；按主花色组批，则需要在所有批次生产完成后，再进行齐户组装，不仅延长了生产周期，而且增加了齐户工序的人力成本。两种组批方式在生产管理与成本方面的优势与劣势见表9。在选择组批方式时须结合订单特点及企业自身的条件，综合评估两种组批方式的成本和管理难度，选择合适的方式。还可以通过板材利用率回归模型进一步创建组批方式的综合成本模型纳入大规模定制家具ERP平台中，有助于提升企业的数字化管理水平，更加便利企业管理人员决策[14-15]。

表9 按主花色与按来源地址组批优劣势对比Table 9 Advantages and disadvantages of the batch rules by main color or by order source address

3 结 论

板式定制家具生产过程中，组批方式对板材利用率有着重要的影响。不同组批方式的板材利用率受不同因素的制约。本研究通过相关分析、回归分析、T检验等统计学方法对A企业两条不同组批方式产线利用率数据进行分析，得出以下结论：

1)零售订单采用按主花色组批方式，利用率回归方程Y=0.361X1-0.074X2+0.011X3+72.762(X1=批次容量，X2=花色，X3=单量)，可以通过增加批次容量、减少花色、增加单量，在一定范围内提升板材利用率。

2)样品订单采用按来源地址组批方式，利用率回归方程为Y=1.356lnX+67.163(X=单量)，板材利用率随单量增加而提升。

3)连续采集一段时间的样品订单数据，分别按照两种组批方式组批排样，通过配对T检验的方法比较两种组批方式板材利用率的差异。结果显示按主花色组批利用率显著高于按来源地址组批。

4)通过回归方程可以大致预测板材利用率，进而预测板材成本，但企业须综合考量各方面因素，比较不同组批方式的优劣，或采用组合的方法，获得最优的组批方式。