基于熵和波形特征的木材损伤断裂过程声发射信号处理

张美林，李俊萩，张晴晖，何鑫，蓝增全，李明

(西南林业大学大数据与智能工程学院，昆明 650224)

木材是一种具有多孔、层状结构的天然复合材料，当其局部发生形变和断裂时，能量以应力波的形式释放出来，从而产生大量的声发射(acoustic emission，简称AE)信号。木材的损伤或破坏方式非常复杂，但从细观结构变化行为来看，木材内部的损伤大致可分为胞壁屈曲与塌溃、胞壁界面损伤与层裂、微裂隙损伤区的形成与扩展、胞壁断裂等几种基本形式，而每一种损伤或断裂在其生成发展中都会有明显的声发射特征[1]。因而，通过对木材在加载状态下的AE信号进行分析和研究，从而推断出其内部的状态变化，并反演破坏过程，对木材内部损伤的研究，以及实时监测和评估具有重要意义。

现代声发射技术的开端在20世纪50年代初的德国[2]，我国直到80年代初AE技术开始应用于工程实际当中[3]。Reiterer等[4]采用劈裂试验和AE监测相结合的方法，研究软木和硬木Ⅰ型断裂内应力变化和断裂过程。孙建平等[5]研究山杨在动态载荷下AE信号的演变过程，通过AE信号的幅值与能量等参数分析研究不同受力阶段木材的AE信号特征。邵卓平等[6]以无缺陷和含裂纹试件为研究对象，在弯曲破坏的条件下研究材料内部微结构演化的AE特性，并用AE事件数、振铃计数、持续时间以及Felicity比等特征参数对几种损伤类型进行辨识。郭晓磊等[7]利用参数分析法研究木材损伤断裂过程中AE信号特征。Lamy等[8]通过力-位移曲线分析、声发射测量和数字图像采集3种实验方法的比较，研究了单调加载下花旗松的破坏过程。Friedrich等[9]探讨了从AE信号的实验记录中计算出的几个指标，以及它们在描述结构破坏过程中的效率，并将其敏感性与声发射分析中通常使用的其他经典参数进行了比较。董红平等[10]、鞠双等[11]通过信号瞬时频率研究AE事件发生数或频谱等特性。

上述研究证明了木材损坏过程中AE信号的幅值、累计能量、振铃总计数、瞬时频率、频谱等常规参量均能够在一定程度上对木材损坏过程进行反映。不过，由于环境噪音的干扰，信号采集系统的设备不同，不同树种、含水率等状态的改变均可能导致相应参数发生变换，从而导致误判。因此，研究并寻找更加敏感和准确的信号特征，同时剔除无用的干扰信息，不仅有助于提高判断的准确性，同时能够提高木材损伤状态预警的实时性。

相关研究表明，木材在受力发生断裂的过程中，激发生成的AE信号具有不确定性、复杂性、非平稳以及非线性等特点。而目前通过信号的不确定性和波形特征来对木材损伤状态下的AE信号进行分析的相关研究较少。由于信号的熵值能够对信号的复杂程度、紊乱程度进行表征，信号的峰值因子、脉冲因子、裕度因子、波形因子等时域特征参数能够敏感地反映出波形的变化。因而，本研究通过采集木材在弯曲损伤过程中的AE信号，利用经验模式分解算法(empirical mode decomposition，EMD)对干扰进行抑制。同时，分析并挖掘木材损伤和断裂状态与信号特征的对应关系。

1 AE信号处理与特征计算

由于EMD算法充分考虑了信号本身的局部尺度特征，使得每个分解分量自然地表示原信号的一种尺度特征，非常适合非线性、非平稳信号的分析处理。因此，本研究首先采用EMD算法对AE信号进行分解，对各个分量信号进行分析处理，保留携带了更多木材断裂信息的分量，去除干扰分量，然后再重构AE信号。最后，再对重构后信号的熵值、峰值因子、脉冲因子、裕度因子、波形因子等特征值进行计算与分析。

1.1 EMD原理与信号重构机制

EMD的基本原理是把一段离散数据信号分解为不同频率的本征模函数(intrinsic mode function, IMF)，以及一个频率接近为0的残余分量。它是由美国学者Huang等[12]于1998年首次提出的，其可以表示为：

(1)

式中：X为原始信号；Ci为IMF；r为残余分量。

在信号处理中，瞬时频率是信号最重要的特性，它是时间的单调函数，在给定的时刻只有唯一频率值，瞬时频率把信号截至为“窄带”，直观上，瞬时频率为相位的微分。峭度反映波形分布特性的数值统计量，当信号存在较多冲击成分时，峭度值明显增大。当木材因受外力内壁发生变化时，能量以应力波的形式释放出来，表现为AE信号，峭度值越大说明信号中冲击成分所占的比重越多。而有效AE信号往往包含于冲击成分较多的信号中，其中峭度值较大的IMF分量中冲击成分较为明显，携带了更多的木材断裂信息。一段信号经EMD分解，根据式(2)[13]计算各IMF分量的峭度，其中Ti为第i个IMF分量峭度。

(2)

由于现有研究表明木材AE信号主要分布在50～200 kHz范围内，并且，木材损坏过程中，AE信号具有较大能量，以及较多的冲击成分。因此，本研究综合考虑各分量的能量、瞬时频率，以及能反映信号冲击成分多少的峭度值，从多个分量中确定并选择有效分量，再对信号进行重构。

1.2 熵函数的意义

熵在信息论中是十分重要的一个概念，它从平均意义上表征了随机对象的总体信息不确定度。对于一个离散随机变量X，将其概率空间设为：

(3)

其中概率p满足：

则整个概率空间的平均不确定性即信息熵定义为：

(4)

在解决实际问题中，为了避免事件ai出现的概率趋于0时不收敛的情况，岳嘉颖等[14]在研究中提出了指数熵的概念，设事件ai的概率为p(ai)，则其包含的信息总量定义为：

ΔI[p(ai)]=e1-p(ai)

(5)

则整个概率空间的指数熵H定义为：

(6)

信息熵和指数熵的概念都是用于描述信息源的冗余度，一段信号越是有序，信息熵就越低；反之，一段信号越是混乱，信息熵就越高。

1.3 信号的波形特征参数

峰值因子、脉冲因子、裕度因子、波形因子等时域特征参数能够敏感地反映出波形的变化，常被做为异常波形检测的特征参数。设某离散信号序列X=(x1,x2,…,xn)，n为信号长度，各波形特征参数的计算如下。

峰值因子XC是信号峰值差(Xpeak)与均方根值(Xrms)的比值，代表峰值在波形中的极端程度。表达式为：

(7)

脉冲因子XI是信号峰值差(Xpeak)与整流平均值(Xarv)的比值。表达式为：

(8)

裕度因子XL是信号峰值差(Xpeak)与方根幅值(Xr)的比值。均方根的公式是信号平方和的平均值的算术平方根，方根幅值是算术平方根的平均值的平方。表达式为：

(9)

波形因子XS是均方根值(Xrms)与整流平均值(Xarv)的比值，及脉冲因子和峰值因子的比值。表达式为：

(10)

综合来说，峰值因子、脉冲因子和裕度因子的物理意义是相似的，都是用来检测信号中有无冲击的指标及波形平缓程度的。波形因子是脉冲因子和峰值因子的比值，其也间接代表了一段信号的极点波动情况。

2 试验设计

2.1 试验样木及设备

选用表面无缺陷且气干状态下含水率稳定在11%左右的榉木(Makino)为实验材料，试件尺寸为800 mm(长)×60 mm(宽)×30 mm(厚)。本研究实验设备为NI USB-6366高速采集卡、LabVIEW软件搭建3通道AE信号采集系统、UTM5105型万能力学试验机(最大试验力为100 kN，功率为1.5 kW，可实现全曲线的绘制)、SR150N单端谐振式AE传感器(信号带宽为22～200 kHz)，同时配备了增益为40 dB前置放大器，每个通道的最高采样频率为2 MHz，放大器的输出电压范围为±5 V。

2.2 试验过程

本研究采用三点弯曲实验激发生成AE信号。通过UTM5105型万能力学试验机对试件进行横向加压，跨距为200 mm，并以1 mm/min的速度对试件匀速加载，整个加压时间持续370 s。在压头两侧分别布置3个AE传感器，每2个传感器的距离设定为300 mm，实验结构图如图1所示。并且在传感器上涂抹硅胶作为耦合剂，保证采集信号更准确。

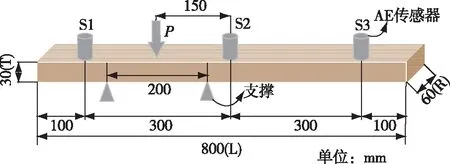
图1 实验设置Fig. 1 Experimental setting

试件表面加压产生的AE信号由传感器SR150N转换为电信号，经前置放大器对信号进行放大，然后使用NI USB-6366数据采集卡采集并转换为数字信号存储在计算机中。数据采集过程是在基于LabVIEW软件搭建数据采集系统的控制下实现的。本研究将数据采集卡的采样频率设置为500 kHz，根据香农采样定理，理论上可以辨识0～250 kHz范围内的AE信号。

3 结果与分析

图2 时间-载荷曲线Fig. 2 Time-load curve

3.1 原始数据分析

为了分析应力与AE信号发生的关系，利用力学试验机绘制了相应的时间-载荷曲线(图2)。从图2可以看出，载荷的变化大致可以分为3个阶段。在一开始时，载荷随着时间线性增加，并在204 s左右达到最大值。宏观上，样木也就在该时刻发生了明显的断裂。随后，在很短的时间内，载荷曲线出现一个陡峭的下降。再之后，载荷曲线以近似于指数曲线的趋势逐渐下降。

采集获取的原始AE信号见图3，根据采样频率和持续时间计算可知，共有1.85×108个采样点。通过观察分析图2和图3，根据波形的幅值或能量，从木材细观结构损伤形变行为来看，可将其大致分为3个阶段：0～110 s，基本没有AE事件，此阶段木材处于弹性变形时期，其内部没有明显损伤产生，其产生的形变为可恢复变形；>110～204 s，有较多幅值较小的AE事件，此阶段木材处于弹塑性阶段，载荷不断增加，试件内部有微小的断裂，木材被加压变形，内部部分结构发生不可恢复性形变；204 s之后，AE事件频度明显增多，且幅值较大，此阶段处于塑性阶段，木材发生宏观断裂，随着荷载的增加，不可恢复程度显著增大，直至试件完全断裂。从图3可以看出，试件载荷达到204 s之前已有较多的AE事件，可以推断出木材内部已经产生了微裂。因此，AE信号能够比宏观形变更加敏感地反映出木材内部损伤状态的变化。

图3 原始AE信号Fig. 3 Original AE signals

不过，仅通过AE信号时域波形的幅度或能量还无法准确判断和分析不同断裂时期AE信号的特征。例如，当采集系统的放大倍数较小或噪音较大时，很难根据幅值或能量将110 s之前和之后的数据区分开来。并且，通过比较图2与图3中204 s之后的曲线，很难直接从AE信号中判断出载荷下降的趋势。因此，本研究尝试研究波形的复杂程度以及波形的形状与木材内部损坏状态的关系。

3.2 AE信号的EMD分解和重构

按照前述的信号预处理方法，首先对原始AE信号进行EMD分解。其中，5×104个采样数据经分解后各IMF分量所对应的时域信号见图4。从图4可以看出，信号能量主要集中在前5个IMF分量中。根据分解得到的各IMF分量信号计算出的峭度值和瞬时频率均值见图5。由图形及计算结果分析可知：AE信号经EMD分解后，前2个IMF分量归一化峭度值最大，峭度值大的IMF分量包含更多的AE信号，且信号频率从IMF1到IMF10逐层降低，高频信号主要集中在前4个IMF分量中。因此，综合考虑信号能量、信号的峭度和瞬时频率选择前4个IMF分量作为主IMF分量对AE信号进行重构。

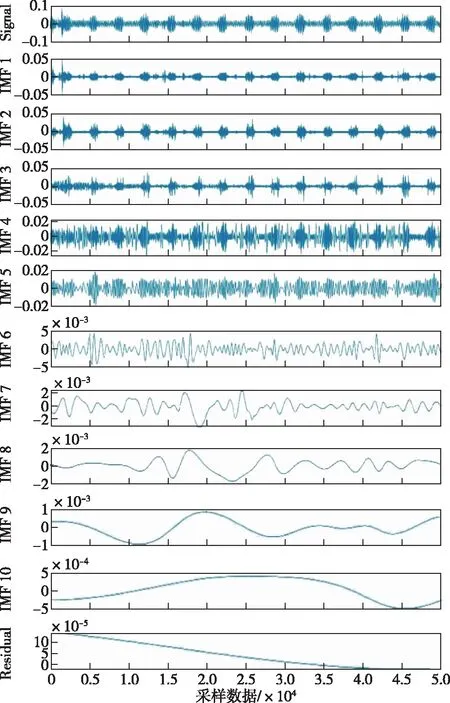
图4 声发射信号EMD分解Fig. 4 Acoustic emission signal EMD decomposition

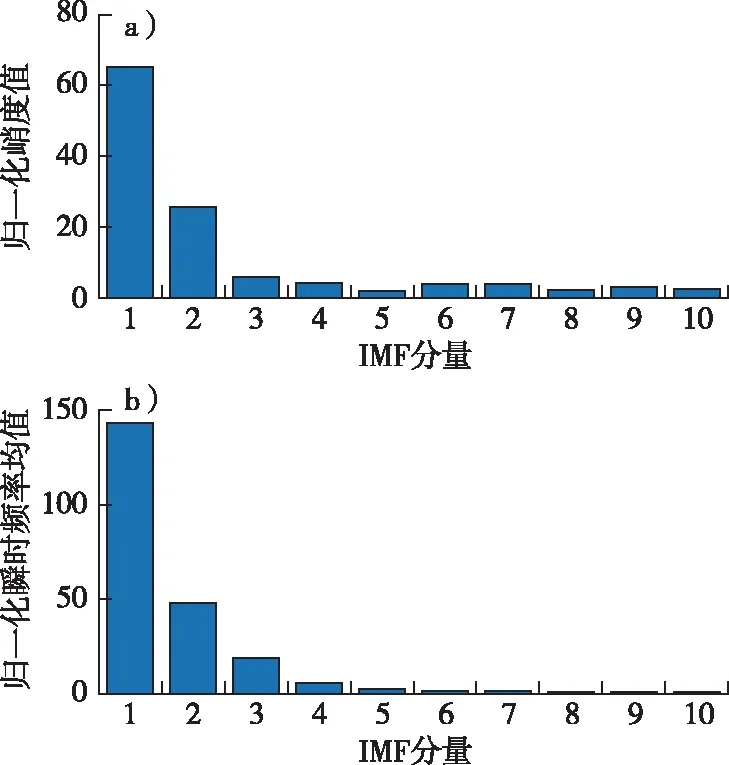
图5 归一化峭度值/瞬时频率Fig. 5 Normalized kurtosis value/instantaneous frequency

3.3 特征分析

为了解木材整个试验过程应力状态及损伤程度，将经EMD分解重构后的AE信号进行特征值提取，并观察整个试验过程AE信号特征的变化。为了能够实时处理数据，在考虑采样率的基础上，将0.01 s的数据作为一个子集，分别计算重构后信号的熵值(信息熵和指数熵)以及波形特征参数(峰值因子、脉冲因子、裕度因子、波形因子)，再结合损伤过程中微观结构变化进行分析。

3.3.1 熵值特征分析

熵值曲线见图6，可以看出信息熵与指数熵的绝对值的波形基本相似，在后续描述中，直接使用熵来代表信息熵和指数熵的绝对值。根据图6中熵值曲线的包络，很容易将其大致分为0～100 s，>100～150 s，>150～200 s，>200～370 s 4个阶段，再结合已有的研究成果[1,6-7]，可知：

第1阶段(0～100 s)，由于信号均是杂乱无序的噪音信号，因此熵的均值是4个阶段中最大的。偶有几个熵值的突变，对应于少量的AE事件的发生。因此，这一阶段与因木材胞壁屈曲与塌溃而产生的少量AE事件的情况相吻合，称此类信号为屈曲AE信号。

第2阶段(>100～150 s)，熵均值较第1阶段有一定的减小，且有较多的熵值突变。说明此阶段有较多的AE事件发生，且信号幅度值的分布较为集中。这与因木材胞壁界面损伤与层裂而产生的平稳且幅值较小的AE信号，木材发生形变的情况相吻合，称此类信号为形变AE信号。

第3阶段(>150～200 s)，熵的均值在整个过程中最小，且有较多熵值突变，但波动较小。表明此阶段有较密集的AE事件发生，且信号的幅值差值最小。这与木材发生微裂时的情况相吻合。这时，因木材微裂隙损伤区的形成与扩展产生相对第2阶段混乱且能量更高的AE信号，称此类信号为微裂AE信号。

第4阶段(>200～370 s)，熵均值低于第1阶段，与第2阶段接近，熵值的突变较多，且波动较大。说明此阶段产生大量混乱AE信号，且信号幅值波动最大。这与因木材胞壁断裂而产生的大量高幅值AE信号，木材发生断裂的状态相吻合，称此类信号为断裂AE信号。

综上所述，与直接采用AE信号的幅度相比较，通过熵值能够更加敏感地与微观结构变化相对应，从而判断出木材的损伤状态。特别是第2～3阶段的差异，可作为木材断裂的前兆。不过，也发现，很难通过熵值图中第4阶段的曲线观察到载荷曲线(图2)所示的逐渐下降的变化。

图6 重构AE信号的熵值Fig. 6 Entropy value of reconstructed AE signal

3.3.2 波形特征分析

重构信号的脉冲因子、裕度因子、峰值因子、波形因子曲线图见图7。从图7可以看出，这4种特征都较好地反映了AE事件发生导致的信号突变。不过，相较于熵值，它们后几个阶段的区分度并不明显。其中，脉冲因子、裕度因子和峰值因子能体现出第1阶段与其他阶段的差异，总体上其特征值均值都是第1阶段<第2阶段<第3阶段<第4阶段。波形因子只能够体现出前3阶段与第4阶段的差异，不过波形因子第4阶段的包络较好地体现了逐渐下降的趋势。

比较图6中信息熵和指数熵的数值分布，从微观上可以看出信息熵在每类AE信号数据分布更明显。同时，比较图7中脉冲因子、裕度因子、峰值因子、波形因子的数值分布，微观上裕度因子更明显地区分每类AE信号的差异。

图7 重构AE信号的波形特征Fig. 7 The waveform features of the reconstructed AE signals

3.4 重构前后特征值比较

通过上述分析已经得到信息熵和裕度因子，从微观上更明显地区分木材损伤断裂过程中各类AE信号的差异。为了进一步比较信息熵和裕度因子哪个更能直观地反映试件损伤过程中信号的特征变化，同时比较经EMD重构前后AE信号的差异，根据不同类别的AE信号，从中抽取6段5×104个采样数据，分别在55，125，185，204，245和315 s，得到重构前后AE信号的信息熵和裕度因子数据，如表1所示。

从表1中的数据可知：

1)比较重构前后信息熵和裕度因子的变化，重构后AE信号的熵值比原始信号低，裕度因子比原始信号高。同时，比较55和125 s的数据，重构后信息熵的差值提高了1.24倍，裕度因子差值提高了1.02倍；比较125和185 s的数据，重构后信息熵的差值提高了1.69倍，裕度因子差值提高了1.01倍。说明经过EMD分解重构后的特征值能更好地区分不同损伤时期AE信号的差异。

2)分析重构后55，125和185 s的信息熵和裕度因子，在55和125 s中，信息熵差值为1.61倍，裕度因子差值为1.06倍；在125和185 s中，信息熵差值为5.98倍，裕度因子差值为3.99倍。因此，相比于裕度因子，信息熵能更明显地反映出不同AE信号的差异。

3)从木材细观结构损伤变化行为来看，在屈曲期，产生少量AE信号，使得信号在某些时间点波动较大，此阶段熵值最高，裕度因子最低；在形变期，AE信号少量增加，使得总体信号波动较小，熵值降低，裕度因子增加；在微裂期，木材临近断裂，内部产生大量幅值较小且密集的AE信号，此阶段信号相对平稳，熵值最低；在断裂期，观察后3段采样数据(204，245和315 s)，其熵值大小都低于55 s(屈曲AE信号)且介于125 s(形变AE信号)和185 s(断裂AE信号)之间，熵值上下波动较大，裕度因子均大于其他3个阶段，说明断裂AE信号比其他3类信号混乱且持续时间长。

表1 重构前后各特征值比较Table 1 Comparison of features before and after reconstruction

4 结 论

本研究表明通过能够反映信号复杂程度的熵值以及波形特征(脉冲因子、裕度因子、峰值因子、波形因子)，可以将木材受力激发出的AE信号分为4个类别，分别是屈曲AE信号、形变AE信号、微裂AE信号和断裂AE信号，并与木材微观结构变化的4种形式(胞壁屈曲与塌溃、胞壁界面损伤与层裂、微裂隙损伤区的形成与扩展和胞壁断裂)相对应。相比较波形特征，AE信号的信号熵值能够更加敏感地反映出木材的内部损伤状态的变化。不过，波形特征能够较好地反映出木材断裂后载荷逐渐较小的趋势。另外，本研究提出的基于EMD的AE信号预处理方法和信号重构机制，能够提高上述特征对不同损伤状态的区分度。

联合使用熵值特征与波形特征，将提高通过AE信号对木材内部损伤状态判断的精度。本研究可以应用于木质建筑、家具、古建筑、音乐设备等木质材料内部损伤的实时监测、评估和无损检测等方面。未来可以通过机器学习算法，自动分类识别不同类型的AE信号特征及其变化规律，进一步研究木材损伤过程弹性能的释放和扩散规律，建立基于能量的木材损伤预测模型。