两相混合式步进电机全速范围无位置传感器速度控制

王春雷， 曹东兴

(1.河北工业大学 机械工程学院，天津 300130；2.天津铁道职业技术学院，天津 300240)

0 引 言

步进电机具有制造成本低，可靠性高和开环控制能力等优势，在工业和各类消费电子领域得到了广泛的应用，如纺织机械，机械臂，扫描仪和3D打印机等[1-3]。

通常，步进电机工作在开环模式，即转子位置和速度分别由脉冲数量和频率控制，运行中不需提供转速和位置信息给控制器。因此，速度曲线在开环控制中扮演着重要角色并得到广泛关注。文献[4]提出了一种用于实时生成速度曲线的算法，可以运行在低端微控制器上，且不限制步进电机从停止状态启动。文献[5]调查了不同加减速曲线的特性及实现，表明相比于常数型和指数型，使用抛物线型速度曲线的步进电机具有较小的位置跟踪误差。

随着电力电子技术和现代控制理论的发展，闭环已广泛应用于步进电机速度和位置控制。文献[6]使用具有良好位置跟踪和负载扰动抑制能力的两自由度比例积分(proportional integral，PI)控制器来调节转速。文献[7]设计了一种适用于开关磁阻电机且易于实现的增益调度PI速度控制器。近年来，人工神经网络迅速发展并已成功应用于电机控制。文献[8]中提出了一种自适应电流控制器，通过使用神经网络来最大程度地减小电流误差，提高了定位精确度。文献[9]提出了一种基于人工神经网络的低速阻尼控制器以消除低速时的非线性干扰，由于其具有学习能力，具有很强的自适应能力。

闭环控制应用中，磁场定向控制(field-oriented control, FOC)广泛应用于步进电机的位置和速度控制[10]。FOC使用机械传感器(如光电编码器)测量的转子位置信息来实现派克及逆派克变换。但机械传感器对高温和高振动等恶劣环境敏感，此外，安装在转轴上的机械传感器会增加电机成本和体积。为克服这些问题，无位置传感器控制被提出并广泛应用于永磁同步电机[11-12]。大多数无传感器控制可分为高频信号注入法和反电动势法。高频注入法与模型无关，适用于零速和低速区，而反电动势方法是模型相关的，适用于中高速区域。

本文研究在全速范围内实现步进电机无位置传感器的速度控制方案，采用混合开闭环控制，提高电机能效。低速时采用微步提高定位精确度，提出全步、半步和微步的定子绕组参考电流调制方程。在中高速，通过滑模观测器(sliding mode observer, SMO)估计的转子速度和位置来实现FOC，提出在每个控制周期内无需使用高计算量的派克及逆派克变换的参考电流调制方案，减少微处理器计算量，可以运行在低端微控制器。

1 两相混合式步进电机的数学模型

简化的两相双极性混合式步进电机模型包括一个永磁转子和两个相隔90°的定子绕组。忽略负载扰动，其状态方程[13-14]表示为：

(1)

式中：ua，ub和ia，ib分别表示定子绕组a和b的电压和电流；B是粘滞摩擦系数；J是转子转动惯量；Km是电机转矩常数；R是定子绕组的电阻；L是定子绕组的电感；ω是转子机械(角)速度；θe=Nrθ是转子电角度；Nr是转子齿数；θ是转子机械(角)位置。

为了消除状态方程(1)中的非线性项，定义电压和电流的派克变换[13]分别为：

(2)

(3)

式中：ud、uq、id和iq分别表示直轴电压、交轴电压、直轴电流和交轴电流。对状态方程(1)进行派克变换并整理可得：

(4)

一般情况下，瞬时转矩τ由电磁转矩和磁阻转矩组成[15]。其中电磁转矩由绕组电流和磁通量相互作用产生的转矩与定位转矩τd组成，由于定位转矩不会显著影响电磁转矩，可忽略不计。磁阻转矩τr取决于两个轴之间的磁阻变化，通过控制id=0将其置零。基于上述假设，瞬时转矩简化为

τ=Kmiq。

(5)

2 无位置传感器速度控制设计

2.1 传统无传感器速度控制

传统无传感器速度控制由一个级联控制器和一个滑模观测器组成，如图1所示。级联控制器由内部电流环和外部速度调节环构成，内、外控制环分别用来调节绕组电流和控制电机转速。滑模观测器估计转子位置和速度，估计的转速提供给外部速度环以实现速度闭环，估计的转子位置提供给内部派克及逆派克变换来实现FOC。

图1 传统无传感器速度控制框图

通过状态方程(1)，得到固定坐标系a-b下的电流微分方程：

(6)

式中ea和eb分别是定子绕组a和b的反电动势，分别为：

(7)

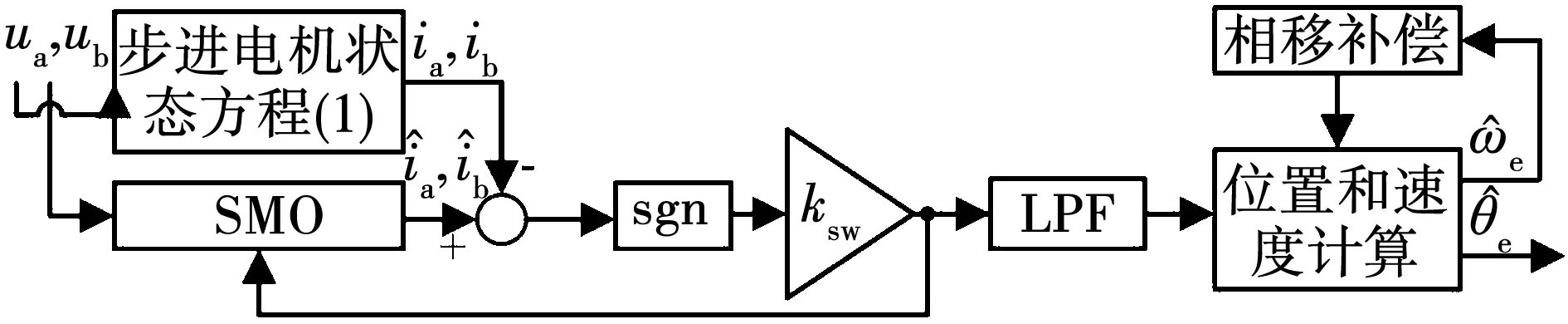
图2 基于滑模观测器的转子位置和速度估计器框图

根据滑模变结构理论和电流微分方程(6)，构造电流观测器：

(8)

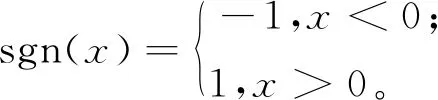
(9)

为验证滑模观测器的稳定性，定义李雅普诺夫(Lyapunov)函数

(10)

式中s是电流误差向量，为

(11)

(12)

将Lyapunov函数对时间求导

(13)

式(12)代入式(13)并展开

(14)

ksw>max(|ea|,|eb|)，

(15)

就可以确保滑模运动存在和全局范围内的渐近稳定性。

当系统轨迹到达滑动表面时，有

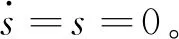
(16)

根据等效控制原理，式(16)代入式(12)：

(17)

反电动势中包含高次谐波，需先滤除高次谐波：

(18)

式中ωc是低通滤波器的截止频率。使用反正切函数计算转子电角度和电转速分别为：

(19)

最后，设计相移补偿模块来补偿由低通滤波器引起的相位延迟来提高估计数值的准确度。

2.2 新无位置传感器速度控制

传统无传感器速度控制中，每个控制周期内都需要使用派克和逆派克变换来完成电压和电流在静止a-b和旋转d-q坐标下的变换。其中：派克变换将a-b坐标下定义的绕组电流ia和ib转换为d-q坐标下的电流id和iq，而逆派克变换将d-q坐标下的电压ud和uq转换为a-b坐标下的电压ua和ub。派克和逆派克变换中包含着大量高计算量的三角函数运算，因此，这些坐标变换操作消耗了大量处理器运算资源。

为此提出一种适用于步进电机且可以运行在低端微控制器上的新型无传感器速度控制方案，如图3所示。新方案使用PI控制器依据参考电流对绕组电流进行调节，其中参考电流由所提电流变换方程提供。值得注意的是，所有状态量都定义在固定a-b坐标下的，不再使用派克和逆派克变换将电压和电流在a-b和d-q坐标间转换，显著减轻微控制器计算量。

图3 新无传感器速度控制框图

首先，通过外部速度PI的输出iq调制a-b坐标下的参考电流iaref和ibref，其次，利用两个具有相同结构的PI控制器根据参考iaref和ibref分别调节电流ia和ib。所提电流变化方程定义为：

(20)

式中τ是由外部PI速度控制器调制的瞬时恒转矩。为实现瞬时恒转矩控制，设id=0，文献[14-15]报告了类似的结果。

使用PI控制器调节两电平脉宽调制器(two-level pulse width modulation，two-level PWM)的占空比来调节绕组电流，因此，具有很高的动态性能。忽略电流动态性：

(21)

对绕组电流ia和ib进行派克变换：

(22)

可见，即使没有使用派克变换，所提方案输出恒转矩。对d-q坐标下的电流向量[idiq]T应用逆派克变换，其中id=0且iq=τ/Km，得到a-b坐标下定子绕组的参考电流分别如下：

(23)

可见，获得的参考电流和使用传统坐标变换得到的结果一致。

图2中使用的滑模观测器可以直接用于该无传感器速度控制结构中。符号函数实现简单，但其不连续性会引起抖振。为减少抖振，用连续的S形函数(Sigmoid)代替不连续的符号函数，S函数定义如下

(24)

式中α为正整数，用来确定曲线的形状。

符号函数替换为S函数后，滑模观测器稳定条件可以通过构造李雅普诺夫函数并利用李雅普诺夫稳定性定理获得，最终得到与使用符号函数一致的结果[10，16]。即ksw>max(|ea|,|eb|)，则滑模运动存在且全局范围内渐近稳定。

2.3 微步原理与开闭环控制切换策略

在中高速范围内，使用滑模观测器估计的转子位置和速度信息实现了速度闭环。闭环改善了步进电机的扭矩-速度特性。此外，由于步进电机以最佳方式驱动[2]，提高了能源效率。由于基于反电动势实现的无传感器速度控制的局限性，在低速范围驱动器需切换到开环模式运行。开环模式下，可以通过全步、半步和微步驱动步进电机，采用全步和半步驱动，参考电流调制方案简单，但定位精确度低且扭矩脉动大。

开环控制通常选用较大幅值的参考电流来产生足够大的扭矩以避免失步。微步的关键是控制电流按照正弦规律变化。提出的统一了全步、半步和微步的参考电流调制方程为：

(25)

式中：N表示微步分辨率N=1,2,4,…32…；m表示参考电流序列索引m=0,1,2,…,(4N-1)；IR表示参考电流幅值；iaref和ibref分别是绕组a和b的阶梯参考电流序列。当N=1时步进电机工作在全步模式，该模式下每次只给两个定子绕组之一供电，转子一次只移动一个整步。相应地，N=2步进电机工作在半步模式，步进电机每次移动半个步距角。可见，通过增大N来减少步进角就可以改善步进电机的定位精确度。

在全速范围内，控制器采用混合开闭环控制策略来驱动步进电机。因此，运行过程中控制器需要根据参考速度适时调整控制策略。当步进电机需要从静止状态加速到参考速度时，首先判断参考速度所处速度区域，然后选用相应的策略。当参考速度处于低速区(小于300 r/min)，控制器按照梯形速度曲线规律使用微步驱动电机到参考速度。相应的，当参考速度位于中高速区，控制器首先采用微步并按照梯形速度曲线规律驱动电机，当加速到参考速度且稳定后，切换到基于滑模观测器的闭环模式。减速模式采用了类似策略，不在赘述。

3 实验验证

实验装置包含一个两相双极性混合式步进电机，一个连接到电机转轴上用来测量转子速度和位置的2 500线光电编码器，一个直流开关电源和一个电机驱动器，如图4所示。表1和表2分别列举了步进电机和控制器的关键参数。实现了无传感器速度控制的驱动器具有适应性强、高效和高可靠性的特点，已应用于一个带有康复模块的智能轮项目中[1]。智能轮椅上共安装了13个不同型号的步进电机，例如，两个大功率电机安装在机架上用于驱动轮椅的平地行使；另外两个步进电机安装在前腿机构中用于前腿姿态的调整。因此，设计满足不同使用场景及高可靠性的电机驱动器是亟待解决的问题。

图4 实验装置

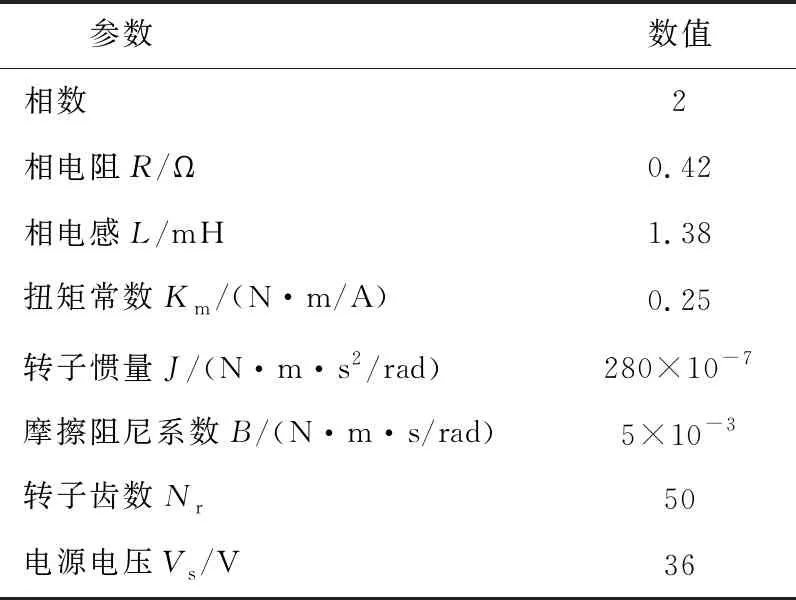
表1 步进电机参数

表2 控制器参数

驱动器由主控制器芯片，两个H桥电路，定子电流采样电路和故障诊断电路组成，如图5所示。主控芯片使用了德州仪器的TMS320F28035，它由一个高效的32位定点CPU，一个增强的脉冲宽度调制器(ePWM)模块，一个增强的正交编码器脉冲(eQEP)模块，一个12位的模数转换器和一个JTAG接口组成。H桥由绝缘栅双极晶体管(insulated gate bipolar transistor, IGBT)实现，为步进电机提供电流。通过测量安装在H桥下桥臂IGBT和电源地之间的旁路电阻的电压来计算定子绕组的实际电流。通过实时测量电源电压、电源电压的变化及定子绕组电流，控制器可以保护驱动系统免受过电流，过电压和欠电压等造成的损坏。当异常发生时，控制器瞬时复位ePWM的输出EPWM1A，EPWM1B，EPWM2A和EPWM2B，H桥工作在续流模式，即电流仅流经下桥臂IGBT和定子绕组。由于没有电源驱动，电流衰减为零，实现了过电流等保护。

图5 步进电机驱动器框图

图6为速度跟踪实验，空载模式下，参考速度按照300～400～500 r/min的规律变化。由于使用较大的控制器增益来保证高动态性，速度脉动存在，稳态时，速度跟踪误差为零，如图6(a)所示。参考速度每0.1 s调整一次，当参考速度调整时，跟踪误差存在，约0.1 ms后减小为零。图6(b)～图6(d)报告了参考速度分别为300，400和500 r/min时，在前半个速度控制周期，测量和估计的转子电角度。此外，表示转子电角度的锯齿波的频率在0～0.1，0.1～0.2和0.2～0.3 s分别为250，333.3和416.7 Hz。相应地，参考速度为5，6.7和8.3 r/min。可见，转子的电转速为机械转速的50倍，符合该混合式步进电机转子有50个齿的事实。

图6 参考速度按照300～400～500 r/min的规律变化时，转子速度及位置响应

图7为电机绕组电流调制实验，报告了空载模式下，参考速度按照300～400～500 r/min的规律变化时，电流在静止及同步坐标下的响应。对ia和ib应用派克变换，得到d-q坐标下的电流id和iq，如图7(a)所示，可见，直轴电流id近似于零，而交轴电流iq正比于转速。图7(b)～图7(d)展示了每前半个速度控制周期内直轴电流ia和ib的响应，它们按正弦规律变化且振幅正比于转速，频率分别为250、333.3和416.7 Hz，与相应转速一致。

图7 参考速度按照300～400～500 r/min的规律变化时同步d-q及固定a-b坐标下的电流响应

4 结 论

研究了一种在全速范围内实现混合式步进电机无位置传感器速度调节方案。在中高速，基于滑模观测器的无位置传感器实现了步进电机的速度闭环。在每个控制周期，定子绕组参考电流的调整都是在固定a-b坐标下进行的，不需要使用计算量大的派克及逆派克变换。控制算法以20 kHz的频率运行时，相比于传统的基于坐标变换算法，可减少9.6%的计算时长。低速时，采用微步技术驱动步进电机，提高了开环定位精确度，克服了利用反电动势估算转子位置信息时对于速度要求的限制。通过低速采用微步和中高速采用基于滑模观测器的无传感器速度控制的混合控制策略，使步进电机在全速范围内运行于无传感器模式，提高了步进电机的能效。空载且转速分别为300、400和500 r/min，与仅使用微步开环(IR=4 A，N=8)相比，使用基于滑模观测器的无传感器速度控制策略可节省81、78.5、76%的能耗。

由于转子多齿结构的限制，混合式步进电机的最高转速低于其他永磁电机。在于算法未补偿反电动势，当转速高于900 r/min时，电流的跟踪能力会显著降低。未来工作中，将引入弱磁技术以提高电机的最高转速并改善其扭矩-速度特性。