基于HSS的三相VSC频率耦合导纳建模与谐波特性分析
朱婷, 胡海涛, 陶海东
(西南交通大学 电气工程学院,四川 成都 611756)
0 引 言
近年来,随着分布式发电系统、储能及微电网的广泛应用,电力电子变流器在电网中的数量大幅提升[0-3]。由于电力电子设备的非线性特性,并网时可能会引起从几赫兹到千赫兹以上的宽频带振荡事件,同时会向电网注入大量谐波,导致电能质量下降[4-6]。另外,随着变流器数目的不断增加,不同变流器间或变流器与电网间的谐波交互作用愈加复杂,从而对电网的稳定运行提出了新的挑战[7]。
在电力电子变流器中,交流侧阻抗通过开关调制与直流侧阻抗产生频率耦合,因此谐波交互现象主要出现在变流器中[8-9]。建立能够分析谐波交互问题的电力电子变流器模型,是目前的研究热点。表1给出了变流器不同建模方法的比较。小信号平均法是线性时不变(linear time-invariant,LTI)的单输入单输出(single-input single-output, SISO)模型[10],只能用于低频区域控制器设计及稳定性分析;基于谐波线性化的描述函数法提高了在高频区域的建模精确度,但依旧是SISO模型,不能分析多个串联或并联变流器在高频段的交互作用[11-12];谐波状态空间(harmonic state-space,HSS)模型是一种基于周期轨迹线性化和线性时间周期(linear time-period,LTP)理论的多输入多输出(multiple-input multiple-output,MIMO)模型,它既适用于分析单变流器,也适用于分析多变流器系统。

表1 不同建模方法的比较
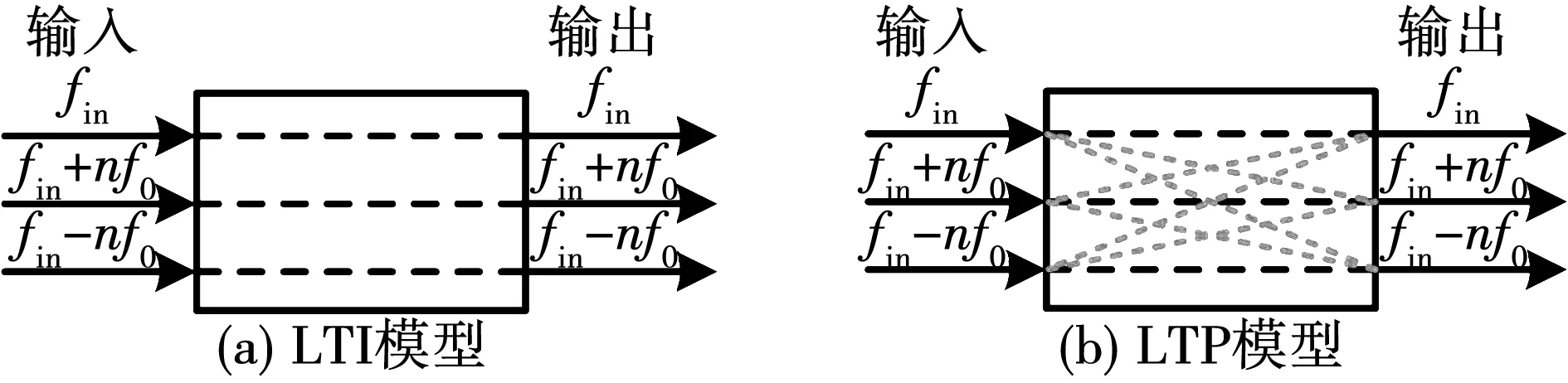
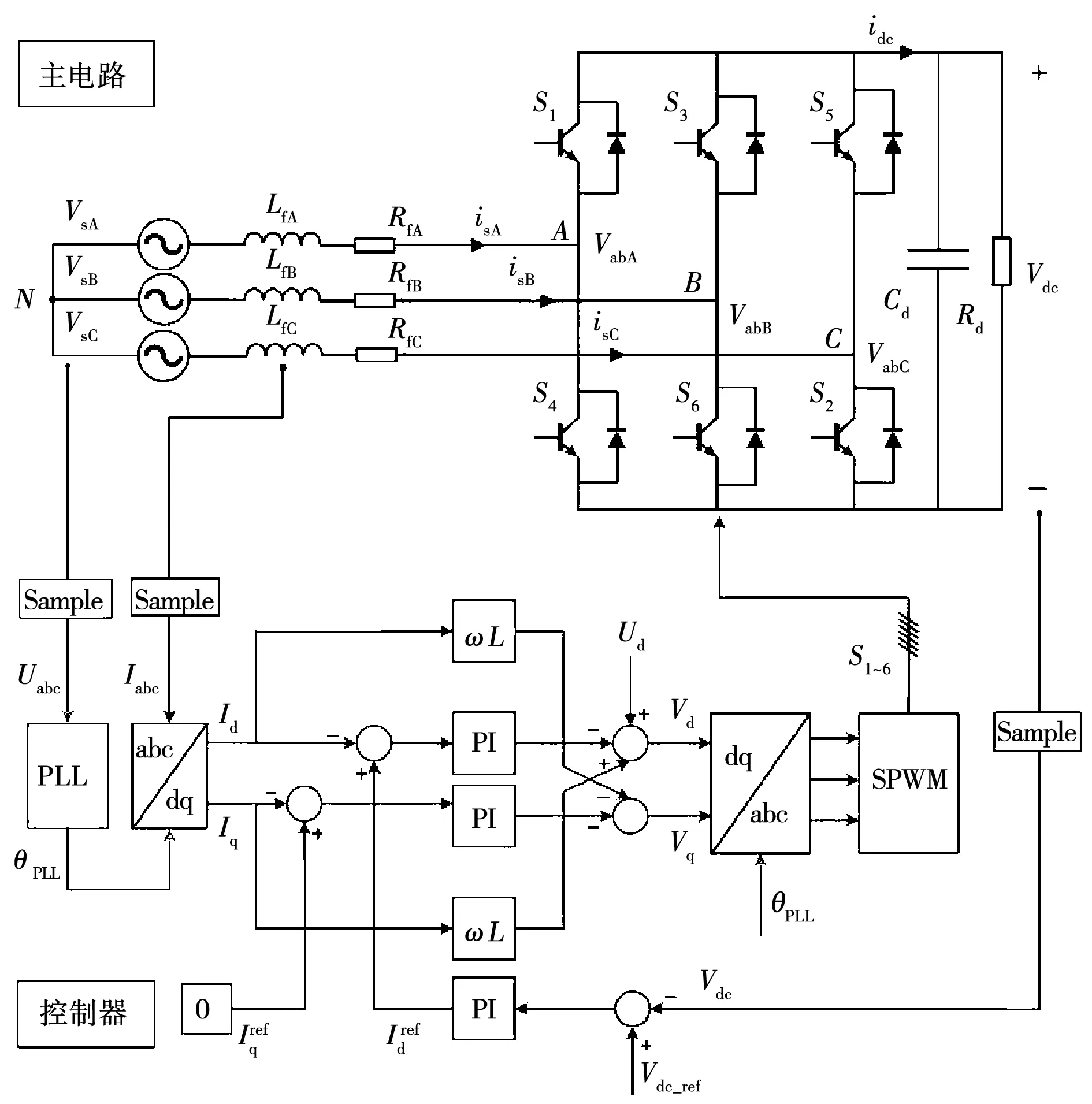
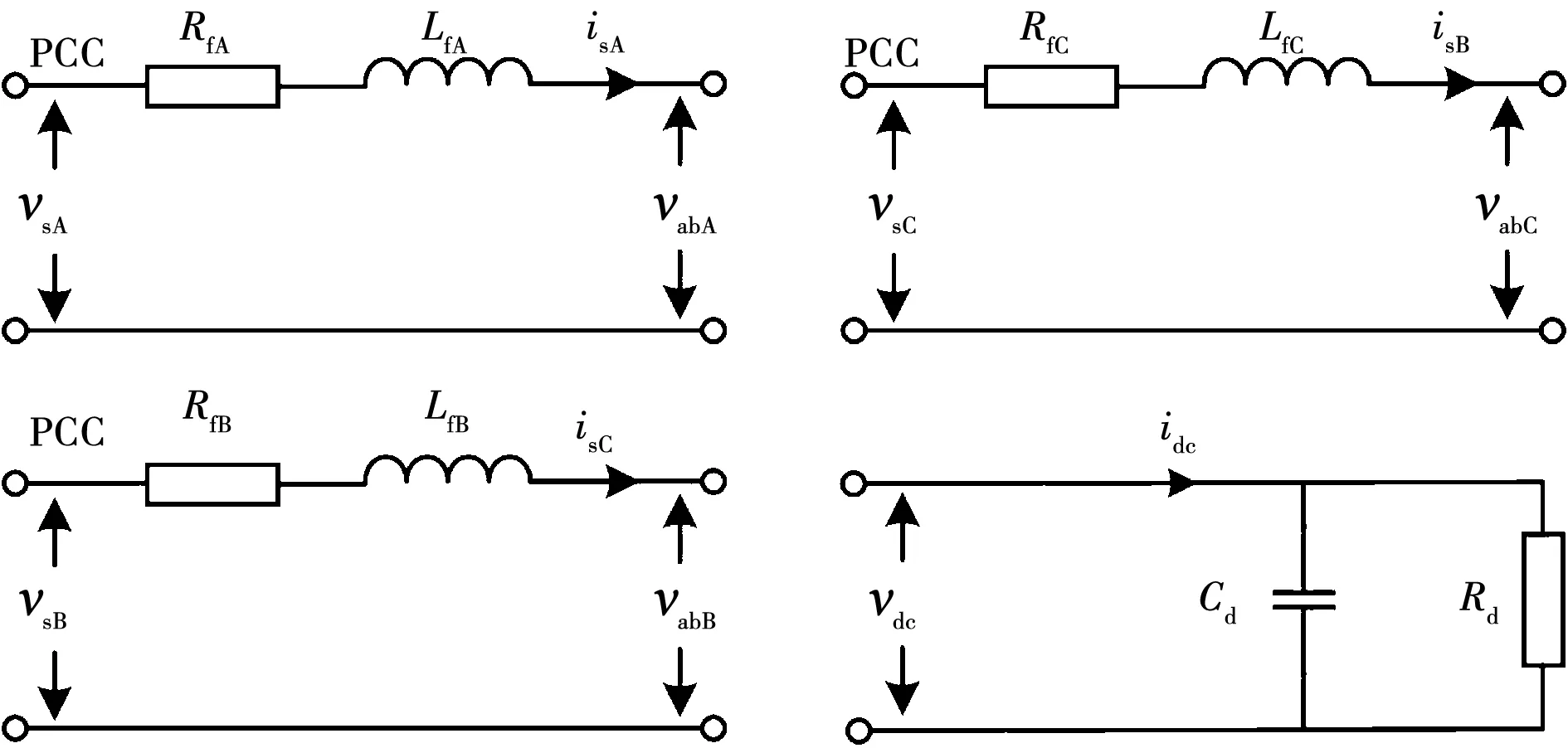
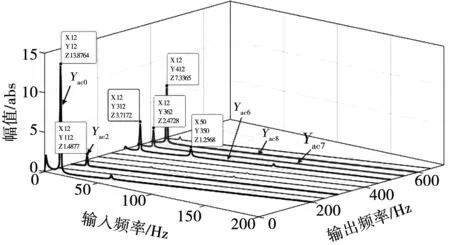
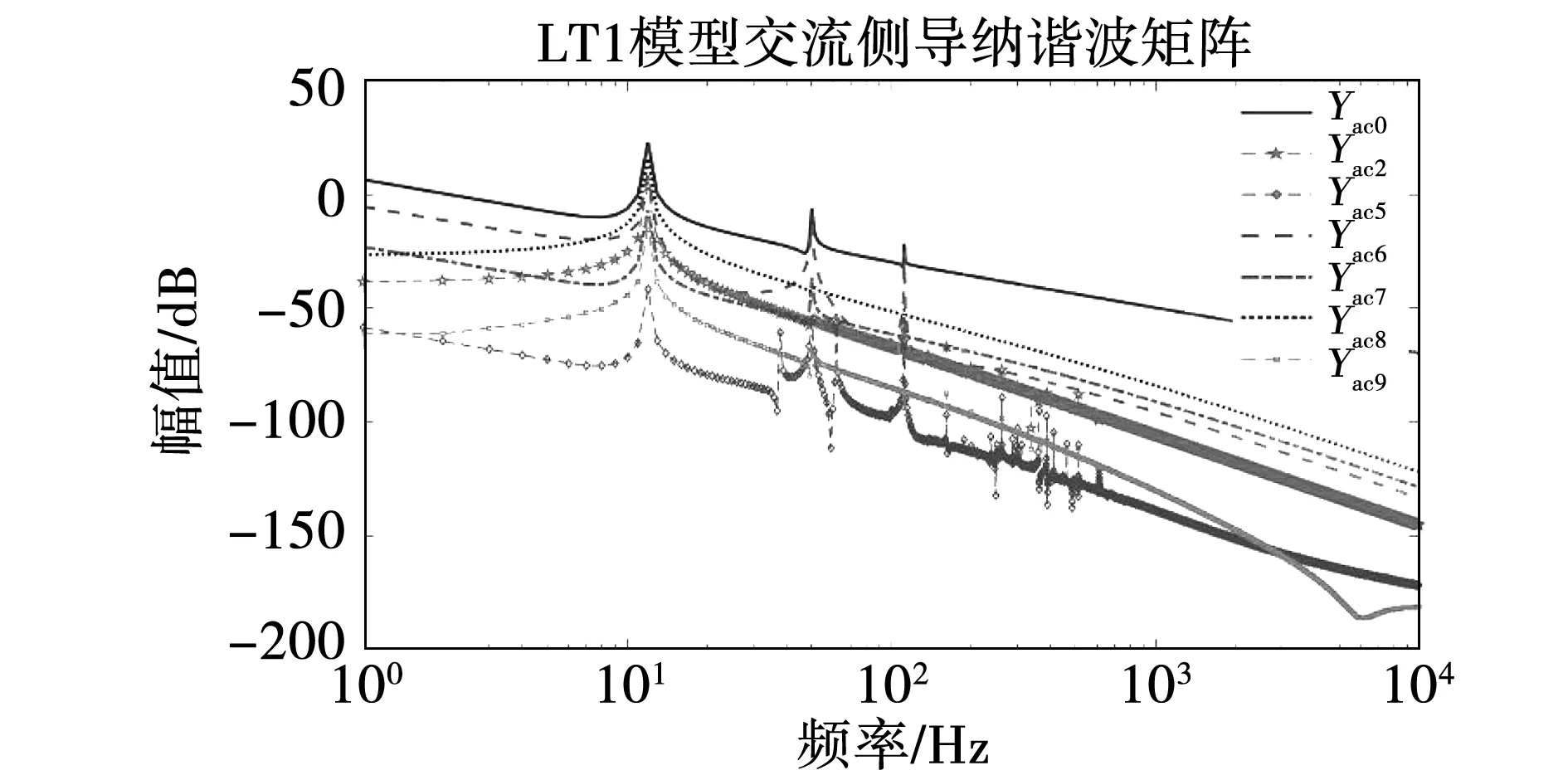
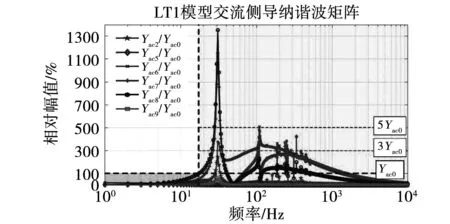
其中:低频(f≤2f0)、中频(2f0 早在1991年Werely基于LTP理论,在线性时间周期信号中加入指数调制周期信号(exponentially modulated periodic signals,EMPS),并结合谐波平衡原理,首次提出HSS模型的概念[13]。Geoffrey N.Love利用HSS法对Buck-Boost电力电子变流器建立了线性化模型,指出可以用HSS模型对动态小信号进行建模及稳定性分析[14]。王雄飞教授团队利用HSS模型对变流器进行谐波分析,指出电力电子元件的开关过程不仅会带来特征谐波,还会带来无限数量的边带谐波[15]。岳小龙博士验证了Buck变换器的MIMO特性,即输入信号与输出响应的关系,不仅是从扰动频率到扰动频率,还包含从扰动频率到耦合频率的情况[8]。但由于交流变换器开关调制的占空比不再是一个恒定的常数,因此调制过程的建模比直流变换器复杂很多。为考虑交流调制过程及开关元件产生的边频影响,王跃教授团队对MMC变流器建立HSS模型,揭示了变流器内部谐波交互的机理[16];已有学者分别建立了电压型控制变换器的多频模型和HSS模型[18]。然而,上述文献大多仅考虑电流内环进行建模,对既含电压外环又含电流内环的双闭环结构研究较少。 本文利用基于LTP理论的HSS建模方法对含复杂双闭环控制的三相两电平电压源型变流器进行建模和分析。创新之处在于对三相电压源型变流器(voltage source converter,VSC)建立了完整且通用的HSS模型,并明确给出频率耦合导纳矩阵的计算方法,分析和讨论耦合导纳在不同频段对变流器输出谐波的影响。首先简要介绍了LTP理论及HSS建模步骤,并对三相VSC建立了HSS模型;其次对比分析所推导的HSS模型与传统LTI模型在谐波交互现象中的区别,揭示谐波的频率耦合现象;最后,将谐波传递函数(harmonic transfer function,HTF)矩阵的稳态响应与Simulink仿真以及RT-LAB实时仿真结果进行比较,验证模型的准确性。 本节将介绍HSS方法的一般建模原理,为后续三相VSC系统的HSS模型建立奠定理论基础。在LTI模型中,电路被简化为线性时不变系统,状态空间模型中的系数为不随时间变化的常量。然而,在LTP模型中系数A(t)、B(t)、C(t)、D(t)为周期时变量,即 (1) 任何周期信号x(t)都可以由傅里叶级数表示为 (2) 式中:ω1为基波角频率;Xk为k次傅里叶系数。 为探究系统的动态特性,向Laplace变换的核函数e-st引入周期扩展,可以得到EMPS,即 (3) 式中的每个分量都以基频的整数倍进行指数调制。定义Z为z(t)的各次傅里叶系数组成的向量,Z=[Z-h…Z-2,Z-1,Z0,Z1,Z2…Zh]T;H(t)为谐波指数向量,H(t)=[e-jhω1…e-jω11ejω1…ejhω1]。则式(3)可以表示为 z(t)=estH(t)Z。 (4) 将式(4)得到的EMPS代入式(1),整理变换即可得到: (5) 矩阵AT如式(6)所示,下标“T”表示Toeplitz矩阵,子矩阵Ah表示仅保留系数矩阵的前h次傅里叶系数所构成的矩阵。式中的Q为H(t)求导后的系数矩阵,Q=diag(-jhω1I…-jω1IZMjω1I…jhω1I),I和ZM为与矩阵Ah阶数相同的单位矩阵和零矩阵。其中状态变量X=[X-h…X-2,X-1,X0,X1,X2…Xh]T,变量U和Y具有相同形式。 (6) 通过推导式(5)可以得到谐波传递函数(HTF): H(s)=CT[sI-(AT-Q)]-1BT+DT。 (7) LTP模型的H(s)是一个双边无限矩阵,矩阵中各元素表示将输入信号的各次谐波映射至输出信号各频次谐波的传递函数。如图1所示,在传统LTI模型中仅有相同频率输入/输出变量的传递关系,不同频次谐波间不存在耦合关系;而LTP模型的时变特性会导致输入频率与基频的整数倍谐波间发生频率耦合现象,即fout=fin±nf0。 图1 两种传递关系的对比 如式(8)所示,LTP系统的HTF矩阵结构可以很好的说明耦合现象。以考虑的谐波次数h=2为例,当输入信号为U0时,由于HTF矩阵中含有非主对角线元素H±1、H±2,因此输出信号中不仅含有与输入频率相同的Y0,还存在耦合频率分量Y±1、Y±2。 (8) 其中Y±1、Y±2分别为输出信号中频率为fin±f0和fin±2f0的傅里叶系数。 当系统达到稳态时,满足条件sX=0。由式(5)可解得任意谐波输入情况下系统的稳态解为 X=-(AT-Q)-1BTU。 (9) 综上,由于HSS模型是在频域中推导建立的,因此模型中所有变量都以频域信息表示,可以通过傅里叶反变换转换至时域[15],即 x(t)=P(t)X。 (10) 式中: 三相并网变流器的框图如图2所示,HSS建模主要包括主电路和控制器两部分。 图2 三相VSC系统框图 主电路交流侧电感(LfA、LfB、LfC)串联电阻(RfA、RfB、RfC)通过三相桥连接到直流侧。直流侧由电容(Cd)并联电阻(Rd)构成电压源型变流器。其次,控制器采用双闭环结构,包括电压外环控制和电流内环控制。 图3为主电路简化框图,根据交直流电路关系,由基尔霍夫电压电流定律,可以得到主电路的小信号线性化模型,如下 图3 主电路简化框图 (11) (12) 式中:vsA、vsB、vsC为交流侧三相电压;isA、isB、isC为交流侧三相电流;vabA、vabB、vabC为开关桥的单相输入电压;vdc和idc分别为直流侧的电压和电流;Cd和Rd分别为直流侧电容和负载电阻;(Δ)表示小信号扰动量。 三相开关桥在任意时刻,同一个桥臂的上下两个开关只能有一个导通,定义开关函数状态为 (13) 式中:“1”表示上桥臂导通,下桥臂关断;“0”表示下桥臂导通,上桥臂关断。 为了在建模过程中包含开关网络的瞬态特性,需要在给定的运行状态下对开关网络进行线性化,微扰线性化后开关桥的数学模型如下: (14) Δidc(t)=isA0(t)ΔswA(t)+ΔisA(t)swA0(t)+ isB0(t)ΔswB(t)+ΔisB(t)swB0(t)+ isC0(t)ΔswC(t)+ΔisC(t)swC0(t)。 (15) 微扰线性化法的本质是在稳态运行工作点处对模型进行一阶幂级数展开[19]。式中的下标“0”表示系统的稳态值,可通过计算或者从仿真结果中得到。 因此,选择主电路输入变量及状态变量依次为ut(t)=[ΔvsA(t),ΔvsB(t),ΔvsC(t),ΔswA(t),ΔswB(t),ΔswC(t)]T,xt(t)=[ΔisA(t),ΔisB(t),ΔisC(t),Δvdc(t)]T,推导得到三相VSC主电路的状态空间模型: (16) 首先通过仿真获取开关函数(swA0(t)、swB0(t)、swC0(t)),交流侧电流(isA0(t)、isB0(t)、isC0(t))和直流电压(vdc0(t))的时域稳态值;再经过傅里叶变换转换至频域。然后根据第一节介绍的HSS建模方法,将A、B矩阵重新组织成如式(6)所示的Toeplitz矩阵形式At、Bt,得到主电路部分的HSS模型 (17) 式中:状态向量Xt=[ΔIsA,ΔIsB,ΔIsC,ΔVdc]T;输入信号Ut=[ΔVsA,ΔVsB,ΔVsC,ΔSWA,ΔSWB,ΔSWC]T。系数进而可以推导主电路的HTF矩阵 Ht=-(At-Q)-1Bt。 (18) 图4 控制器框图 (19) (20) (21) ΔSW=Tdq-abc[ΔVd+ΔIqω0L- (22) 式中Tdq-abc为dq轴变换至abc轴的坐标变换矩阵,有 Tdq-abc= (23) 正余弦函数cosθ和sinθ被重新组织成Toeplitz矩阵的形式,整理可得出控制器部分的HSS模型如下: (24) Yc=CcXc+DcUc。 (25) 式中:控制器状态变量Xc=[ΔX1d,ΔX3d,ΔX3q]T;输出变量Yc=[ΔSWA,ΔSWB,ΔSWC]T;输入变量Uc=[ΔVdc,ΔIsA,ΔIsB,ΔIsC,ΔVsA,ΔVsB,ΔVsC]T;同理可得控制器的HTF矩阵 Hc=-Cc(Ac-N)-1Bc+Dc。 (26) 系统的整体结构框图如图5所示。 图5 系统结构框图 图示中Hc、Ht分别代表控制器和主电路的HTF矩阵,矩阵阶数由谐波次数h决定。图中每个黑色的小方块都代表一个具有Toeplitz形式的(2h+1)阶方阵。根据图5的输入输出结构,结合主电路和控制器两部分的HTF矩阵,推导三相VSC系统的谐波传递函数矩阵为 (27) HVSC即三相VSC系统的谐波传递函数矩阵。为方便讨论,改写为 (28) 式中Yac_A、Yac_B、Yac_C分别为交流侧A、B、C三相的输出导纳矩阵。由于三相对称,本文重点对交流侧A相输出导纳矩阵Yac_A进行分析。 通过实现上述模型,得到三相VSC系统的谐波传递函数矩阵HVSC,系统参数如表2所示。 表2 三相VSC系统参数 首先,绘制交流侧A相谐波输出导纳矩阵Yac_A中各分量的Bode图,与LTI模型进行对比。其次,讨论了h的取值对HSS模型准确性的影响。最后建立仿真模型,给出HSS模型和Simulink仿真模型的时域波形对比结果,验证HSS模型的准确性。 在MIMO模型中,HTF矩阵的频率响应特性通常由三维Bode图表示,x轴表示输入频率(fin),y轴表示输出频率(fout),z轴为相应的响应增益。图6所示为交流侧A相输出导纳谐波矩阵Yac_A的三维Bode图。由图可知,输出响应中不仅含有输入频率的谐波分量,还包含与基频f0的整数倍耦合产生的谐波分量。本文仅对基频的正整数倍耦合产生的谐波分量进行分析,即fout=fin+nf0,图6也验证了三相VSC系统的MIMO特性。 图6 矩阵Yac_A三维波特图(h=9) 图中Yac0(s)是Yac_A矩阵中的主对角线元素,即LTI分量;其余的为非主对角线元素,即耦合分量。Yac0表示当n=0,即输出频率等于输入频率(fout=fin)的幅值曲线,Yac4则表示输入输出频率满足fout=fin+4f0时的幅值曲线。由图可知,耦合分量Yac2、Yac6、Yac7、Yac8在一些对应的输入频率时,会出现较大的数值,从而导致输出信号中包含许多高频耦合分量。此时,Yac_A矩阵为非对角占优矩阵。这种现象说明了将耦合频率分量考虑至建模过程中的必要性。 本文所建立的HSS模型,可以任意设定所含谐波次数h的大小。当h值越大,模型中包含的耦合分量越多,阶数越高,模型就越准确。HSS模型中交流侧A相输出谐波导纳矩阵为 Yac_A(s)= (29) Yac_A是一个具有Toeplitz矩阵形式的2h+1阶方阵,如式(29)所示(h=2)。矩阵中主对角线元素Yac0为LTI分量,非主对角线元素Yac1、Yac_1、Yac2、Yac_2为耦合频率分量。 图7所示为HSS模型交流侧导纳矩阵Yac_A中各分量的Bode图。在低频范围内,LTI分量Yac0的幅值高于其他耦合分量(Yac2、Yac5、Yac6、Yac7、Yac8、Yac9),因此可以忽略频率耦合带来的影响;但随着频率上升,在中高频范围内耦合产生的Yac6、Yac7、Yac8分量逐渐大于主对角线分量Yac0,导致其不再占据主导。为比较HSS模型与传统LTI模型的区别,在Simulink中搭建了三相VSC系统的LTI模型,其中三相变流器的开关桥式电路选择平均模式。图8为LTI模型谐波导纳矩阵Yac_A中各分量的Bode图;从图中可以看出,与HSS模型的不同点在于主对角线分量Yac0在全频域范围内始终为主导频率分量。为能更加直观的看到,HSS模型中耦合分量对模型的影响程度,绘制了其较LTI分量的相对幅值图,如图9所示。由图可知,在中高频范围内,耦合分量Yac6的绝对值大小超过LTI分量的3倍;Yac7、Yac8甚至高于5倍LTI分量。因此在这些频率范围内,耦合分量的影响较大。 图7 HSS模型交流侧导纳谐波矩阵 图8 LTI模型交流侧导纳谐波矩阵 图9 HSS模型中耦合分量的相对幅值图 综上分析可得以下结论:由开关动态产生的部分耦合分量在中高频率范围内,数值会上升到与主频率相近,甚至远超主频率,从而取代了LTI分量的主导位置。而传统LTI模型由于在建模过程中忽略了开关动态,导致耦合项在全频域范围内数值很小。但在实际工程应用中,不可能完全忽略开关动态的影响。因此直接忽略耦合项的LTI模型,不能准确描述三相VSC系统中出现的所有谐波分量。而本文提出的HSS模型,在建模过程中可包含所有频率耦合分量,提高了模型的准确性。 根据式(29)中的HTF模型,通过式(10)将HSS模型的谐波频率响应转换至时域,可以得到三相VSC系统HSS模型中交流侧A相电流(iac_A)和直流侧电压(udc)的稳态时域响应。并在Simulink中搭建仿真模型。首先对HSS模型选取不同的模型阶数h,讨论了h的取值对模型准确性的影响。当h=1时,Toeplitz矩阵中只包含LTI分量,HSS时域波形与传统LTI模型结果一致。随着h值增加,HTF矩阵阶数越高,能包含更多的频率耦合项,HSS模型的计算值就越接近仿真值,模型越准确。但h取值过高,会导致模型过于复杂,使得计算速度大幅下降,因此对于h值的选取需折衷考虑。如图10所示为Simulink仿真、h=20时的HSS模型以及LTI模型的对比结果。由图可知,HSS模型的计算值与Simulink仿真的时域波形基本吻合,而传统的LTI模型却不能准确描述出三相VSC系统的高频特性。 图10 时域验证 为进一步验证本文提出HSS模型的准确性,在RT-LAB平台中搭建图2的三相VSC系统,并利用OP5700仿真机进行实时仿真,仿真参数如表2所示。实时仿真结果如图11所示,其与计算值保持一致,验证了HSS模型的准确性。 图11 RT-LAB实时仿真结果 本文采用基于LTP理论的HSS方法对三相电压源型变流器建立数学模型,推导出能描述输入输出频率耦合关系的谐波传递函数矩阵。对比了LTI模型和HSS模型在分析谐波特性及其耦合机理时的区别。具体结论如下: 1)在低频范围内,HSS模型和LTI模型一致,HTF矩阵的非主对角线元素都低于主对角线元素。此时,输入输出谐波间的耦合作用影响较小,可以忽略。 2)随着分析频率升高,由于开关动态的影响,部分非主对角线元素会取代主对角线元素成为主导,此时若仍忽略非主对角线上耦合分量的影响可能会使得分析结果不准确。而在LTI模型中,由于忽略了开关动态,非主对角线上的耦合分量被衰减得很小,这也是其在高频特性分析中精确度不足的原因。 因此,较传统的LTI模型,本文所建HSS模型同时考虑了LTI 分量和所有耦合频率分量,从而具备更高的模型精确度。提供了一种分析变流器频率耦合及谐波特性的有效工具,所提模型可应用于分析由频率耦合生成的不期望谐波所引起的谐波谐振及谐波不稳定现象。基于本文已有的工作,后续将开展的研究是:对电力电子并网系统进行谐波分析及稳定性评估。1 HSS建模概述

2 三相VSC的HSS建模方法
2.1 主电路建模
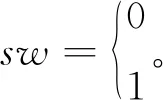
2.2 控制器建模
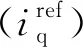

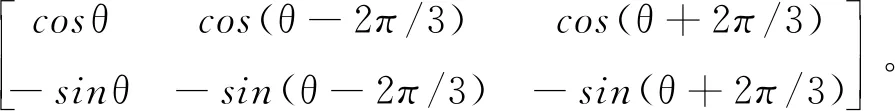
2.3 三相VSC系统的谐波传递函数矩阵

3 仿真分析

3.1 频率耦合导纳分析
3.2 HSS模型与LTI模型的比较

3.3 时域验证


4 结 论

