基于粒子群优化最小二乘支持向量机的铁路客运量预测

王喜燕，刘亚琳

(郑州铁路职业技术学院,河南 郑州 451460)

铁路客运量预测属于非线性系统问题。对于非线性建模问题，首先把非线性问题线性化后再进行处理，方法很多，比如神经网络、支持向量机(SVM)等。文献[1]将神经网络用在铁路客运市场时间序列预测中是为了防止神经网络容易陷入局部最优问题，文献[2]提出基于遗传算法的神经网络铁路客运量优化预测，提高了收敛性。针对神经网络易陷入局部极小值和精度不高的缺点，文献[3]提出用支持向量机的方法来预测铁路客运量。但是，支持向量机采用的是网格搜索的方法来优化正则化参数γ和核参数σ，耗时较长。因此，本研究提出基于粒子群优化最小二乘支持向量机的铁路客运量预测。

最小二乘支持向量机在支持向量机的基础上，改变了损失函数，以误差的二范数来表示，原有的不等式约束用等式约束来代替，由此将二次规划问题转化为线性方程组求解，降低了计算复杂性、加快了求解速度，也提高了收敛速度。由于网格搜索速度较慢，本研究采用粒子群来优化正则化参数γ和核参数σ，经仿真验证比较，不仅提高了预测精度，而且收敛速度也比较快。

1 最小二乘支持向量机

最小二乘支持向量机最早是由Suykens提出的，是标准SVM的一种扩展，LS-SVM比标准SVM待选参数少，其基本原理如下：

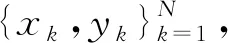
y(x)=ωT·φ(x)+b

(1-1)

从而非线性函数转化为高维特征空间的线性函数。根据结构风险最小化原则，优化问题转化为

(1-2)

S.t.yk=ωTφ(xk)+b+ek,k=1,…,N

其对偶问题的函数

(1-3)

其中，αk是Lagrange乘子。最优解的条件给出如下：

求解方程组，待求量w,b也转化为求αk,b。(1-4)式可以转化成如下的线性方程组：

(1-5)

其中：y=[y1;…；yN],1=[1;…；1];α=[α1;…；αN];Ωkl=φ(xk)Tφ(xl)=K(xk,xl);k,l=1,…,N=0。

(1-6)

最终得到LS-SVM模型为

(1-7)

αk,b是方程组的解，K(x,xk)是核函数，满足Mercer条件，核函数有如下几种形式：

(1)线性核函数K(x,xk)=xT·xk；

(2)多项式核函数K(x,xk)=(xTxk+1)d；

(3)径向基核函数K(x,xk)=exp(-γ‖x-xk‖2/2σ2)；

(4)Sigmoid函数K(x,xk)=tanh(s(x·xk+c))。

一般情况下，RBF是比较常用的核函数，本研究也是基于此函数的。核函数中正则化参数γ和核参数σ的最优参数选择是非常困难的，选择不好，影响泛化性能和准确度。所以，选择好的优化算法来优化正则化参数γ和核宽度σ参数是非常重要的。

2 粒子群

粒子群优化算法是由 Eberhart 博士和 Kennedy 博士于1995年提出的一种基于群智能进化的计算技术。算法初始化为一群随机粒子，通过迭代搜索到最优解。在迭代过程中，粒子通过跟踪个体极值和全局极值更新自身的速度和在下一轮迭代中的位置。找到和后，粒子的飞行速度和新的位置根据它们来决定。

粒子群优化算法根据如下公式更新粒子速度和位置：

(2-1)

(2-2)

式中，w为惯性权重因子，取值范围选作[0.5，1]；c1和c2是学习因子，取值范围选作[1，2]；r1和r2是0和1之间的随机数；i= 1 , 2 , …, m,m是该群体中粒子的总数；d表示一个d维的空间；k为当前迭代次数。

在粒子群的所有参数中，w的选择很重要，较大的w全局搜索能力较好，而较小的w则局部搜索能力较强。所以，在优化过程中，w应在前期有较强的全局搜索能力，后期有较强的局部搜索能力。经验公式

(2-3)

中，t是迭代次数，Tmax是最大迭代次数。

3 基于PSO的LS-SVM建模预测方法分析

用PSO优化LS-SVM得到最佳的参数γ和σ，选择均方误差作为适应度函数。具体算法步骤如下：

(1)初始化PSO参数以及LS-SVM中正则化参数γ和核参数σ；

(2)计算适应度并且判断是否最小，是就更新位置和速度，否就继续优化；

(3)确定最佳LS-SVM中正则化参数γ和核参数σ，再一次训练；

(4)最后用得到的最优γ和σ预测。

4 铁路客运量建模与预测

4.1 数据的分析和处理

根据中国统计数据年鉴可以看出，新中国成立以来铁路客运量经历了1998—2000年1次下跌，以1995—2013年的铁路客运量历史数据作为训练集，2014—2018年的客运量作为测试集，所选数据中包括了1998—2000年的突变情况，如表1所示。

表1 1995年至2018年铁路客运量统计表

首先为了效果更好，进行数据归一化处理；其次为了提高建模精确度，把1995—2013年的训练数据构造成三输入一输出的形式，测试数据也按此形式处理。处理完以后的数据如表2和表3所示。

表2 处理后的训练数据

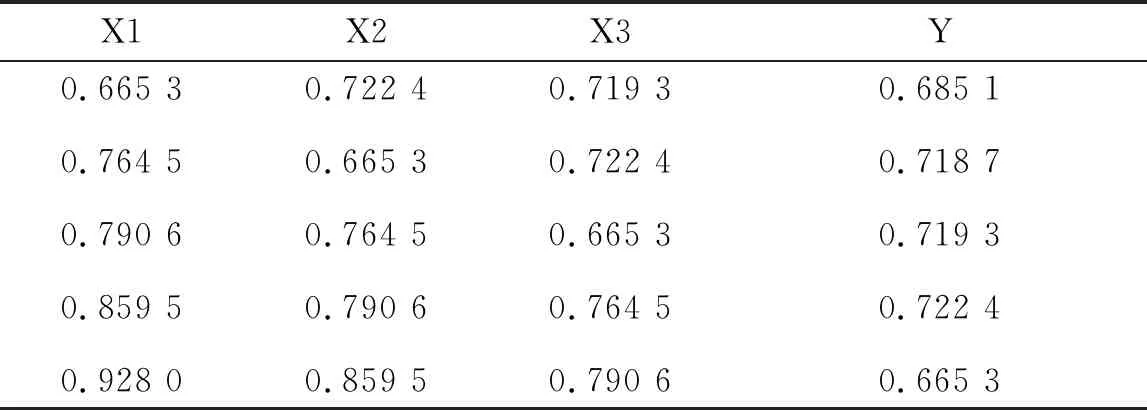
表3 处理后的测试数据

4.2 仿真的结果和分析

用PSO优化LS-SVM的算法仿真上面的数据，对训练数据建模预测得出的结果如图1，可以看出，训练数据的预测效果非常好。

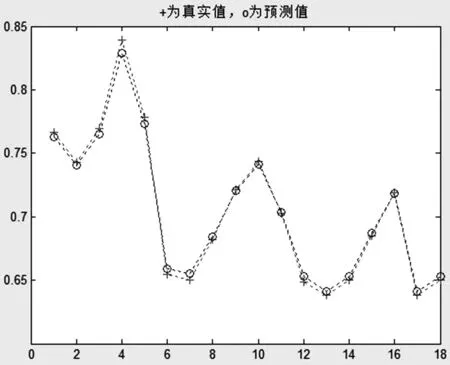
图1 训练数据预测图

再由训练得到的模型预测2014—2018年的测试数据，得到结果如图2。可以看出，在未来1—2年内预测的效果还可以，越往后预测效果越差，说明随时间推移铁路客运量发生了突变，现有的模型也就不适合新的数据。但是，在未来1—2年短时间内此预测的效果还是令人满意的。由图3也可以看出，未来4年的预测相对误差度都差不多不到1%。由此可见，此方法预测效果很好。

图2 测试数据预测图

图3 相对误差图

基于PSO的LS-SVM算法铁路客运量预测相对误差为1%左右，比神经网络的17%左右效果好；基于PSO的LS-SVM算法铁路客运量预测的网格搜索速度为0.456 891 S，LS-SVM为0.800 559 S,粒子群的方法较快。

5 结论

本研究采用PSO优化LS-SVM的参数方法预测铁路客运量，与神经网络和LS-SVM的预测效果进行比较看出，此算法收敛速度快、精确度高、相对误差比较小，对铁路客运相关行业有非常好的指导意义。