基于支持向量法的风电场概率聚类等值方法
常方圆,郑 良,丁 伟
(国际小水电中心,浙江 杭州 310002)
随着全球能源转型升级,可再生能源的作用愈发凸显,在各类可再生能源中,风电是除水电以外发展最迅速的可再生能源之一,近年来随着风电产业的逐步成熟,能够精确表示大型风电场的等值模型研究愈发重要。大型风电场的详细模型包含数十台甚至上百台风力发电机,会增加系统的数学模型规格并且增长仿真时间,用合理的等值方法对各个部件的数学模型进行简化,简化后的等值模型也可以保持较高的精确度。在风电场模型等值方面已有诸多方法,马少康等[1]利用元件连接法的思路建立各个分立元件模型,通过连接构建风电场模型;夏安俊等[4]提出了一种风电场内输入风速不同的多台机组单机等值建模方法,得到风电场等值模型;蒙晓航等[6]提出应用同调等值法对风电场进行简化;耿琳[8]提出基于特征分析的风电场建模;MUHAMMAD ALI等[9]提出由一个单机风电机聚合模型代替整个风力发电场;朱乾龙等[10]提出采用风电机组的转速向量作为分群指标进行分组的方法;任智君等[13]采用改进动态聚类算法进行机群划分,进而基于风电场参数对等值机模型的参数进行聚合辨识。上述文献中采取了不同的建模等值方法,可以在实际仿真中减少一定的计算工作量,减少暂态稳定性分析过程中的仿真时间,使风电场的第一近似值、风电场的性能评估和风电场对电力系统性能的影响变快,但相应地会增加实际应用的难度。当风速或者风向改变时,等值风机的序列和参数也会发生相应的变化,尤其当忽略尾流效应或假定风电场每一点的风力情况都相同时,搭建的仿真模型会过高或者过低地表征风电场的功率输出。
笔者使用了基于支持向量法的风电场概率聚类等值方法,该方法使风电机的等值数量和响应参数可以在风电场建模中重复使用,可用于任意排列的风电场,并且考虑到了因尾流效应[14]及地理位置特性影响引起的风速变化[15],在模型建立的过程中除了风力机和风电场拓扑结构中的电气和机械参数,唯一需要考虑的因素就是建模点的风力参数,如风速和风向。
1 理论背景
1.1 支持向量聚类法
支持向量聚类法(support vector clustering,SVC)是在支持向量机的基础上发展而来的一种聚类方法,针对处理大规模数据速度缓慢的缺点,提出了一种改进的分块支持向量聚类算法[16-18]。SVC算法的目标是分配多维数据组的功能,获得准确且非重叠的簇。每台风机的风速模型作为支持向量聚类算法的输入参数,建立明显非重叠时相的群集。每台风机的有效风速为注入风电场的风速,对于每个目标风速,通过运行支持向量聚类法来形成集群。支持向量概率聚类法根据风力分布情况以及流入风速的大小对风电机组进行概率聚类并分组,通过分析该点风力情况来确定表征风电场的等值风机的台数。
1.2 尾流效应模型
风力带动发电机转子转动时,一部分动能会在转子风速下降时变成更大的湍流,形成尾流。尾流效应的影响不仅取决于风速和风向,也同时取决于动叶片的特性以及风机间的距离,风电场的排列方式对于风速相近的风机有较大影响。详细的尾流效应模型分为单一的、局部的和多重的尾流。本文中尾流效应模型用于在不同风速和风向条件下,确定单台风机处的风速,忽略受风机背后形成的尾流效应影响产生的湍流[19]。
用Jensen模型计算单一尾流产生时,风机处的风速为
(1)
式中:v1为距风力机χ0处的风速,m/s;m为大气稳定度常数;γ0为风力机转子的半径,m;Ct为推力系数;μ为自然风速,m/s。Jensen实验证明m值对于陆地应用为0.075,离岸应用为0.04。
局部尾流产生时,第台风机处的风速为
(2)
式中:β为受尾流效应影响的转子面积与总的转子面积的比例加权系数;k为上风向风力机数;μ为输入k的初始风速,m/s;υps,Tk为k在第j台风机处产生的尾流影响。
多重尾流产生时,计算方法为
(3)
式中:v2为当风机受到同一列的两个上风向风机影响时的风速,m/s。
2 风电场等值模型
应用支持向量概率聚类法建立基于风力分布的聚合模型,当风速和风向变化时,概率模型可以为聚合模型群组提供唯一的风电场表示方法,而不是每一次都需要改变降阶模型的次数。
风电机聚合通过支持向量聚类法来实现,通过预测风速和风向来获得数据,通过尾流效应仿真来计算每台风机处的风速,依据风速和风向分布建立风电机群集。文中选取的算例为国内A地区一个包含9台双馈风力发电机的13.5 MW小型风电场,在不同的风速和浆距角调节情况下,每台双馈感应发电机的额定功率为1.5 MW,风速为4~25 m/s,额定风速为15 m/s。风电场分布均匀,相邻风电机间的距离是100 m(图1)。
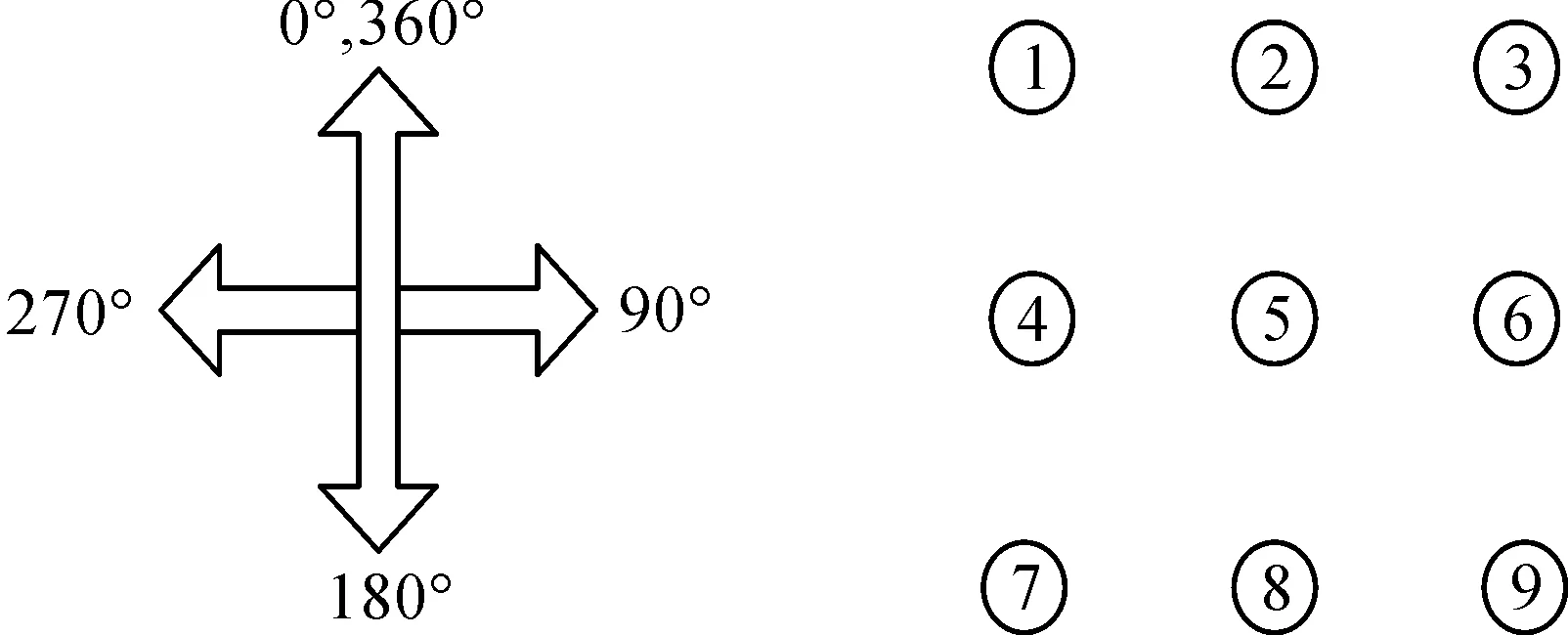
图1 9台双馈风机风电场分布图
2.1 风机聚类分析
表1是在给定风向下,输入风速为15 m/s的风机分群情况,风电机组根据风电场中单台风机接收到的风速分群,比如群组1代表风机接受到较低风速,群组3代表受接到较高风速。群组1中的风机在群组2和群组3的尾流效应影响之下,而群组2只受到群组3的尾流影响。

表1 设定风速=15m/s,不同风向情况的风机分群
应用基于聚类法的等值模型来实现静态或者动态仿真时,需要根据风速和风向不断的变化来重新调整模型参数,因为这会影响集群的数量和集群内风电机的数量。当采用概率聚类法时,这样频繁的参数调整是可以避免的,通过把集群分组,找出一个最合适的群组,可以在较长一段时期内的大部分风力条件下有效工作。风速或风向的变化会影响到风力机聚类的方式,也会影响群组的数量和群组出现的概率,尤其是两种影响聚类结果的特性。
1) 恒定风速,风向变化
由于尾流效应影响,风向的改变影响风电场内风速的变化,继而影响风力机的聚合方式,以及整个风电场的表示方式。
2) 恒定风向,风速变化
当输入风向恒定时,随着风速的增大,表示风电场所需的集群数目减少,当风速高于额定风速时,风电场可等值为一台风力机。
2.2 聚类分组的形成
假设分组方式有几种,分别为X1,X2,X3……为了确定组X的概率,首先应该确定选择该组时风速和风向的概率。例如,当风速为4.5 m/s和6 m/s,风向为100°~120°时,X的概率计算为
(4)
式中:PWS为此时风速概率,PWD为风向概率。
式(4)适用于当风向恒定、风速变化时组X概率的计算,当出现不同的风速和风向组合,如WS=4 m/s,WD为100°~120°;WS=6 m/s,WD为120°~140°,此时,X的概率计算为
(5)
图2和图3分别为笔者算例所采用国内某风电场某年度内实测风力情况的风电场风速、风向概率分布图。
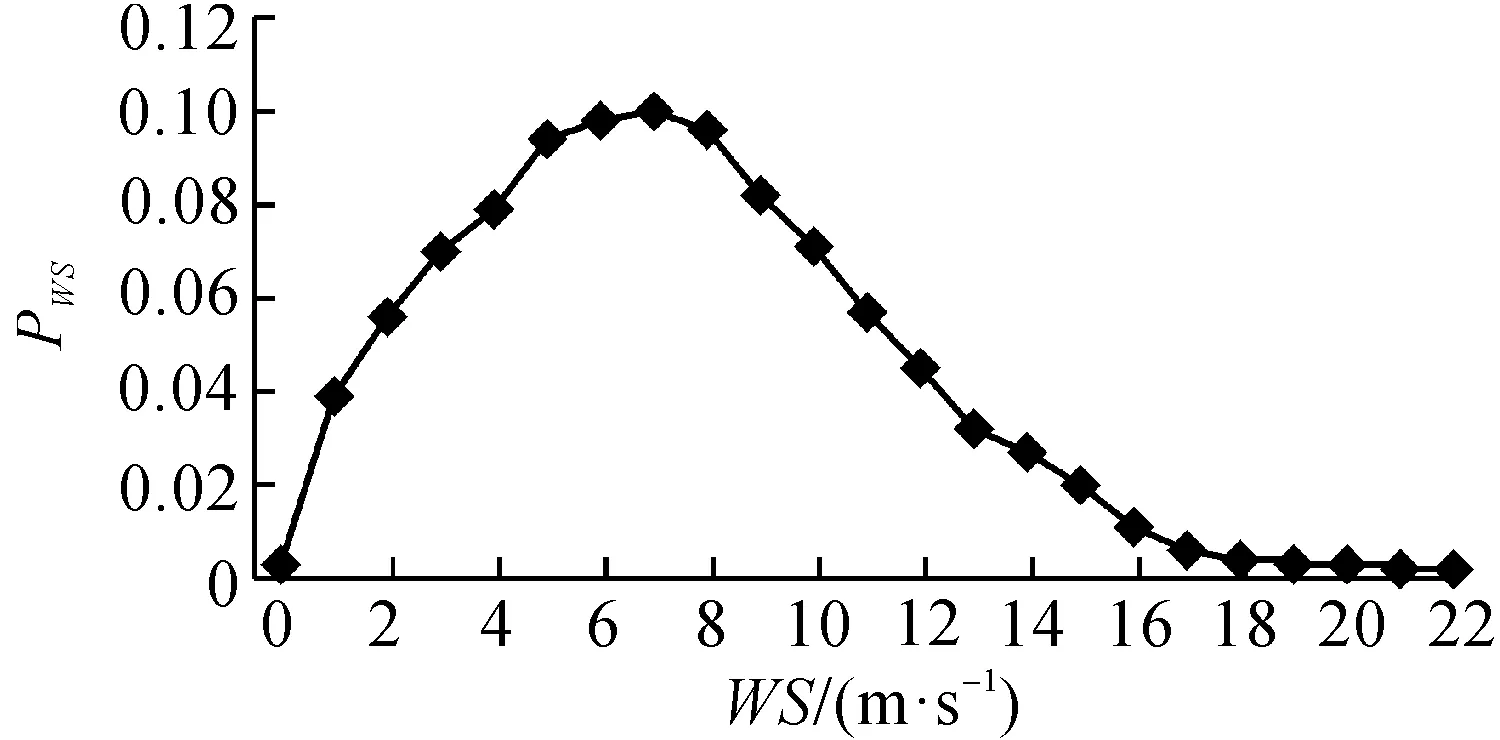
图2 A地区某年度风速概率分布图
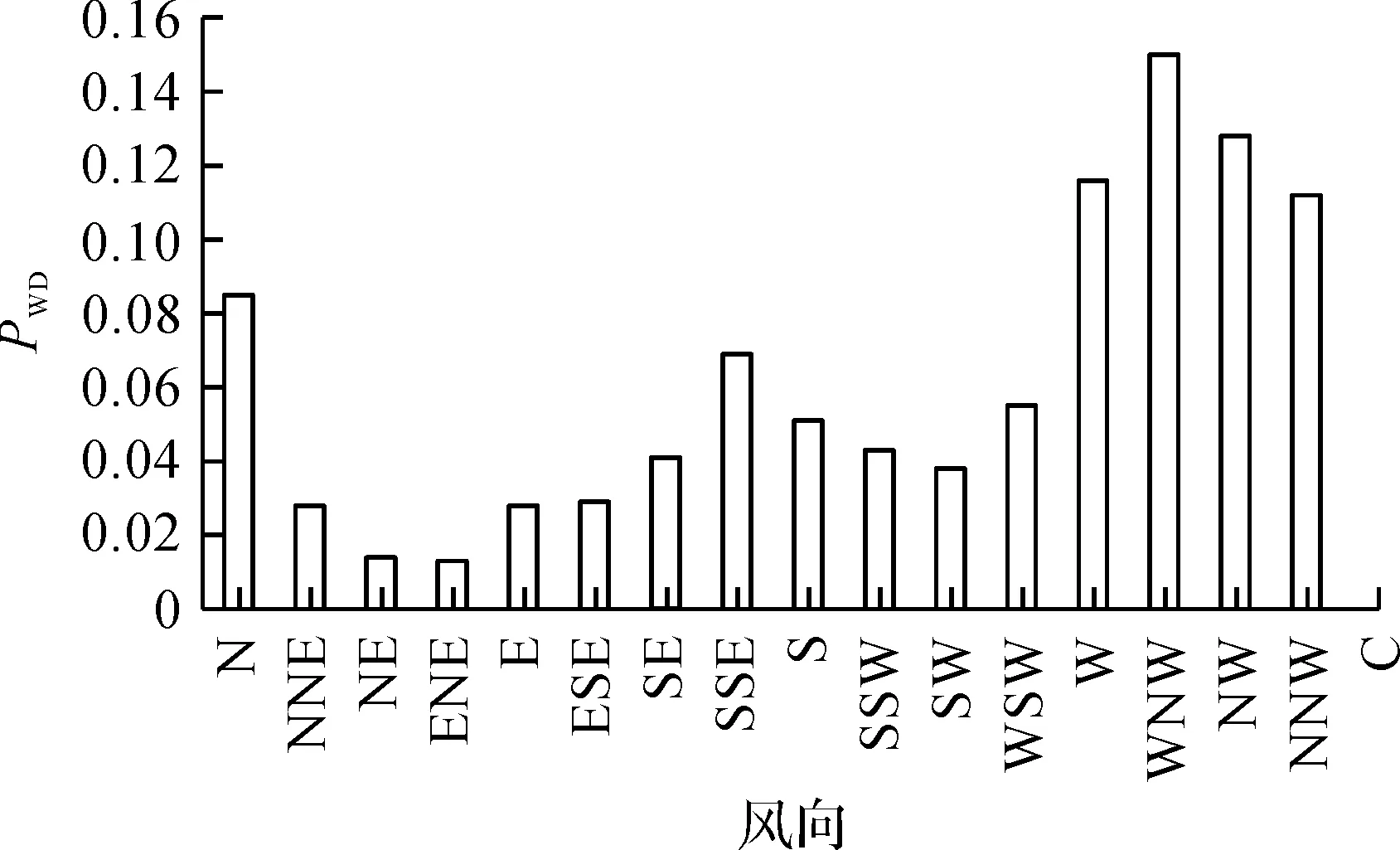
图3 A地区某年度风向概率分布图
结合图2,3的风速、风向概率数据,代入式(4,5)可以计算出一年内任一组的概率,表征风电场的组数目随着方向间隔和该地区风力特性的变化而变化。计算结果如表2所示,选取概率较高的三组作比对,其中分组X1概率高于其他组,所以本算例中用组X1来表示等值风电场。

表2 聚合风电场的最大可能组
3 仿真及动态响应分析
设定仿真条件为:详细风电场模型为9台单机容量1.5 MW的双馈型风力发电机组成的13.5 MW风电场,根据表2中的计算结果,风电场可以用两台风力发电机等值,即等值为1台3 MW和1台10.5 MW的风机。
详细风电场模型和等值风电场模型均通过图4所示方式接入电网,风机端口电压为575 V,风场出口接25 kV,风电场电压通过25/120 kV变压器升压为120 kV,公共耦合节点(PCC)处的电压为1 pu(标幺值),并将120 kV以上电压等级的系统等值为等值电源与等值阻抗。
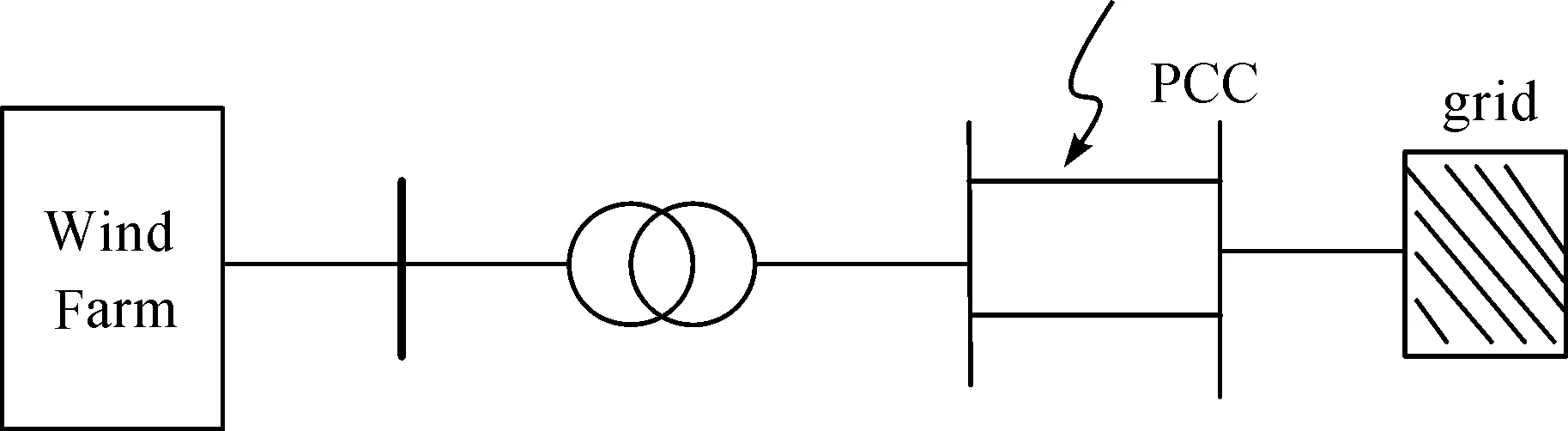
图4 风电场接入电网示意图
设定风场额定风速为15 m/s,风向为ESE(东南东),在连接风电场和PCC的输电线上设计一个100 ms的可自我恢复扰动,开始时间为0.03 s。对比等值聚合模型和详细模型的有功功率和无功功率响应,结果如图5所示。

图5 等值模型和详细风电场模型有功功率和无功功率响应对比
图5中实线部分为风电场详细模型有功、无功曲线,虚线部分为聚类等值风电场有功、无功曲线。从仿真结果可以看出,当输入风电场的风速较低,尾流效应影响较大,风电场中各风机处的风速完全不同,不同的运行点产生的功率也不相同;当风速在额定风速附近时,尾流效应的作用较弱,聚类等值风电场和详细风电场模型并网点有功、无功功率波形非常接近。所以,用基于概率聚类法得出的2台等值机模型表征的风电场可以代替9台详细风电机模型表示的风电场,证明了概率聚类等值方法的有效性。
4 结 论
笔者以支持向量法和尾流效应为理论基础,介绍并验证了基于支持向量聚类法的风电场概率聚类等值方法,该方法用风速测定、风电场排列以及设备电气参数等来确定风电场最大可能性模型,简化的聚合模型很大程度上减少了仿真时间,该等值方法中2组聚类等值风力机模型表示的风电场与9台详细风机模型的仿真结果非常接近。这种方法使得风电机的等值数量和响应参数可以在风电场建模中重复使用,不受风电场任意排列方式的限制,同时没有忽略由风电场尾流效应以及地理位置特性影响引起的风速变化。该方法亦可作为搭建风电并网物理/数字混合仿真实验平台的等值建模方式,是研究风电并网混合仿真系统的风电场建模仿真基础。

