激振力阶次对整体叶盘振动影响分析
卞天天, 杨铮鑫, 党鹏飞
(沈阳化工大学 机械动力工程学院, 辽宁 沈阳 110142)
随着石油化工、能源动力及航空航天等领域的飞速发展,叶片-轮盘结构的设计和研制逐渐受到了更多的关注[1].整体叶盘系统在实际工作过程中受力十分复杂,叶轮转子作为对气体做功的主要部件,长期高强度工作,一方面受到整体叶盘在高速旋转状态下的离心力作用,另一方面受到多种气流扰动下的气流激振力作用[2].因此,在多种复杂工况条件下,整体叶盘由于刚性较低,叶片容易产生共振和颤振,这不仅影响叶轮机械的正常工作,甚至还会造成严重的工程事故[3].
为了有效避免整体叶盘损坏产生机械故障,对整体叶盘在工作中的振动响应特性分析已经成为了研究热点,并取得了很多重要成果.
近年来,许多国内外学者采用不同的研究方法,对整体叶盘的振动展开深入探讨.Kaneko[4]等利用模态叠加法,求解了整体叶盘系统的运动方程,并对其进行数值积分求解,使得整体叶盘振动特性分析更加明确.徐自力等[5-6]利用有限元分析法,建立三维有限元模型,研究了整体叶盘中叶片固有频率和振型在不同状态下的特点.Zhou[7]等利用有限元方法建立了叶片拉筋结构的转子系统模型,对其结构振动特性展开研究.Lim等利用弹簧质量块建立分组拉筋结构叶盘模型,分析了具有分组拉筋结构叶盘的振动特征[8-9].
若将整体叶盘振动响应特性分析研究方向仅停留在叶盘结构上的改变与比较,而忽略激振力对整体叶盘振动响应特性的影响,势必会造成整体叶盘的振动在动力学分析上的缺失和不充分性.因此,也有许多学者对整体叶盘在不同条件激振力下的振动特性展开研究.
田少杰[10]等采用模态叠加原理,基于叶片模态气动阻尼比和气动激振力,分析了整体叶盘系统叶片振动响应特性,并建立了气流激励下的叶片振动响应分析方法.辛建强[11]等通过有限元法和MATLAB软件对整体叶盘响应特性进行分析与处理,对失谐流体激励下的整体叶盘响应特性展开研究.敬彤等提出一种高效的瞬态强迫响应分析方法,模拟旋转的整体叶盘经过流场时叶片表面上的气动载荷,对复杂时变激励下的整体叶盘瞬态响应进行分析[12].
本文基于集中质量整体叶盘物理模型,模拟不同激振力条件下整体叶盘的振动响应变化,研究激振力阶次对整体叶盘振动响应的影响规律.
1 整体叶盘模型及运动方程
建立循环对称结构集中质量整体叶盘物理模型.r假定为此刚性叶盘的半径,N个叶片为固定于叶盘上的集中质量梁,cbj、kbj、mbj是第j个叶片(j=1,2,3,…,N)的黏性阻尼、刚度和质量.所有叶片的质量和黏性阻尼均相等.图1模型中叶片自身阻尼、质量、刚度分别为cb、mb、kb;叶盘间阻尼、叶片间耦合刚度和叶片间阻尼分别为cd、kc、cc.

图1 整体叶盘集中质量模型Fig.1 Lumped mass model of blisk
第j个叶片固有频率为
(1)
设叶片自身固有频率为
(2)
在不考虑非线性因素,同时阻尼cc=0的情况下,第j个整体叶盘的振动方程为
(3)
式中:xj是第j个叶片的位移;Rj为整体叶盘第j个叶片的耦合强度;ωc为等效耦合频率;ωb、Fj、ξ分别是谐调叶片的自振频率、作用在第j个叶片上的激振力和叶片间阻尼比.

循环对称结构在N个叶片条件下的整体叶盘振动方程可用矩阵形式表示为
(4)
在整体叶盘工作过程中,由于其旋转和非旋转部件会受到气流扰动的影响,通常将该扰动模拟为激振力,以和谐形式加载于叶片上,因此作用在叶片上的激振力可假定为
FT=Feiωt{1,eiΦ2,…,eiΦj,…,eiΦN}.
(5)
式中
(6)
式中:Φj为第j个叶片上外力的相角;ω为激振力频率;C为激振力的阶次.
式中
XT={x1,x2,…,xj,…,xN},
(7)
在循环对称的整体叶盘中,刚度举矩阵Kj通常由无损叶片广义刚度kj和耦合广义刚度kc组合而成,即Kj=kj+kc.
对于循环对称的整体叶盘,所有叶片的质量、阻尼、刚度均相等,即x0≡xN,x1≡xN+1,m1≡mj≡mN.因此,(4)式可进一步转化为以下矩阵形式:
(8)
式中
假设整体叶盘的位移为
X=xeiωt.
(9)
式(9)带入式(8)可得
(10)
从式(1)至式(10),通过集中质量整体叶盘物理模型建立了谐调整体叶盘的响应方程.
2 整体叶盘数值模拟
为研究整体叶盘在不同激振力阶次下的响应特性的响应规律,对整体叶盘进行数字模拟.整体叶盘在不同激振力阶次下的响应特性模拟流程如图2所示.

图2 整体叶盘数值模拟流程Fig.2 Numerical simulation flow of blisk
基于上述的叶盘模型,选定基准叶片数N=20,耦合强度R=0.2,激振力阶次C=2,叶盘间阻尼比ξ=0.01.采用MATLAB编程并进行模拟计算,得到不同激振力阶次下的叶片力的分布,以及整体叶盘的响应特性.
按照上述所设参数,根据图2所示的流程进行模拟.通过假定的叶片数量、阻尼比、耦合强度等参数,输入已编好的方程算法,模拟整体叶盘各叶片所受的不同激振力形式下相对振幅(如图3所示).处理各叶片的激振力数据,模拟整体叶盘系统响应特性曲线(见图4).
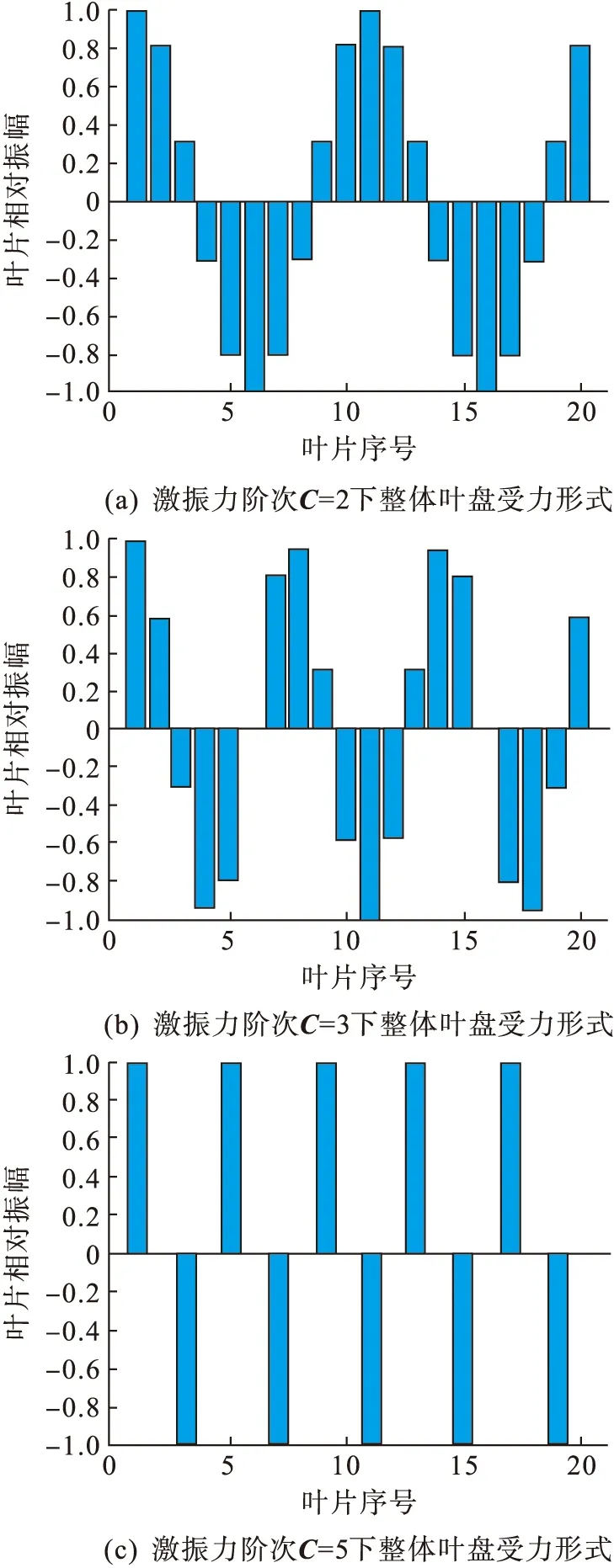
图3 各叶片所受不同激振力形式下的相对振幅Fig.3 Relative amplitude of each blade under different excitation force forms
3 不同激振力阶次C对整体叶盘幅频特性的影响
在质量失谐的整体叶盘条件下,与非一体化整体加工的叶片-轮盘结构相比,整体叶盘中的叶片和轮盘间的耦合关系较强,因此,在对轮盘和叶片的振动响应特性分析时,应将其作为一个整体结构进行分析.当系统的耦合强度发生改变,取C=2、C=3、C=5,而其他参数为基准值时,得到的系统的响应幅频特性如图4所示.
通过图4可以发现整体叶盘在激振力阶次改变的过程中,共振区域没有较大的改变,系统共振发生区域的宽度始终维持在500~700之间,在整体叶盘激振力从低阶次向高阶次过渡的过程中,整体叶盘的共振频率较为稳定.比较不同激振力阶次C下的整体叶盘响应特性可以发现,在系统激振力从低阶次向高阶次过渡的过程中,整体叶盘平均振幅从141.3下降到100.8,最后下降至77.6.

图4 不同激振力阶次C下的响应特性Fig.4 Response characteristics under different excitation force orders C
4 结 论
对整体叶盘不同参数的响应特性进行分析,得到以下结论:
(1) 对于谐调结构整体叶盘系统,激振力阶次对系统共振频率的影响非常小,共振发生区域的宽度没有发生变化,共振频率较为稳定.
(2) 通过比较不同激振力阶次下的响应特性曲线,激振力阶次由低阶向高阶的过程中,系统的振幅逐渐降低,减弱了整体叶盘的振动效果.
(3) 不同激振力阶次下的激振力施加方式和条件是不同的.在设计和制造整体叶盘时,应充分考虑激振力模拟的气流扰动对叶轮机械的影响,指导设计人员采取相应的措施,有效提高整体叶盘的使用寿命.

