线上求解法最优近似格式的探讨及应用
刘 阳, 李 凌
(沈阳化工大学 信息工程学院, 辽宁 沈阳 110142)
现代科学研究过程中,研究人员常常将研究对象抽象成数学模型,进而通过数学建模预测研究对象的变化趋势.在建立模型和仿真的过程中常常需要建立数学方程并进行求解,但在比较复杂的系统中,所建立模型的数学方程经常以偏微分方程的形式出现.求解偏微分方程时常常难以得到精确的解析解,所以想对此类系统进行全面的数值分析就需要对偏微分方程进行离散化,化为常见易解的常微分方程形式再求解.线上求解法(method of line,MOL)是一种常用的求解偏微分方程的方法[1-2],该方法是将一个自变量当成连续变量,再用有限差分法或正交配置法离散剩余的自变量[3],从而将偏微分方程转变为常微分方程组,将问题转化为求解常微分方程组.
在化工过程动态分析[4]中,基于MATLAB的线上求解法思想有着广泛应用.危凤等[5]将线上求解法与MATLAB工具相结合,解决了色谱分离动力学模型的求解与仿真,快速准确地模拟了色谱分离的过程;危凤、沈波等[6]还将基于MATLAB的线上求解法应用于奥美拉唑对映体的色谱模拟分离上,对模拟移动床色谱分离技术制备手性药物化工过程的建模仿真做出了较好优化;在乙烯环氧化反应工业领域,石向成等[7]运用线上求解法思想,建立了该反应的固定床列管反应器数学模型,对乙烯环氧化反应的工艺条件做出了分析;邓家璧等[8]在模拟移动床分离过程的模型预测控制方法研究里,结合线上求解法思想与MATLAB系统辨识工具箱,设计了一个预测控制器对模拟移动床进行控制,取得了较好效果.
本文在介绍线上求解法原理的基础上,通过使用MATLAB软件求解工具箱,对一维Burgers方程进行仿真实验,结合仿真图像曲线分析线上求解法的最优近似格式,并应用于苯加氢管式固定床反应器的化工反应工程仿真建模,验证了该方法的可靠性.
1 线上求解法
线上求解法的求解大致分为两个步骤:(1)对方程中的偏微分项进行离散; (2)在离散后的方程上对时间变量进行积分求解[1].
1.1 偏微分项的离散
偏微分方程
xt=f(t,z,x,xz,xzz),z∈D,t>0.
(1)
边界条件
a(t,z,x,xz)=0,z∈D,t>0.
(2)
初始条件
x(t=0,z)=x0(z),z∈D∪S,t=0.
(3)
其中:t为时间且t≥0;z为空间域D中的位置变量;S为空间域D的边界域;xt为对时间变量的一阶偏微分项;xz为对空间位置变量的一阶偏微分项;xzz为对空间位置变量的二阶偏微分项.
对一阶偏微分项xz先选取空间网格点zi(i=1,2,…,n),再用泰勒级数进行展开,则一阶偏微分项的三点中心近似格式为
Δz=zi-zi-1.
(4)
一阶偏微分项的五点偏心逆风近似格式为
10xzi+3xzi+1)/12Δz+ο(Δz4).
(5)
二阶偏微分项的五点中心近似格式为
32xzi+1-2xzi+2)/12Δz2+ο(Δz4).
(6)
在应用MATLAB软件求解工具箱时可以将式(4)~式(6)用矩阵形式表示.
1.2 时间变量的积分求解
通过采用几种格式近似一阶偏微分项和二阶偏微分项后,可以通过MATLAB软件求解工具箱中的ODE求解器进行求解[3],常见调用格式有ode45、ode23、ode15s等.
2 基于MATLAB的仿真实验
MATLAB现已在工业和学术界广泛使用,仅需要较少的编程专业知识便可获得可靠的仿真实验结果[9],这为MOL工具箱的开发提供了非常方便的基础.针对线上求解法在求解偏微分方程时对一阶偏微分项和二阶偏微分项的离散效果,笔者选取了一维Burgers方程作为模型,分别采用几种不同的离散近似格式,在MATLAB软件下编写程序调用ODE/DAE求解器,输出仿真图像,结合图像进行分析探寻并验证离散效果最佳的格式.
2.1 一维Burgers方程
一维Burgers方程,即为简化的动量平衡方程,如式(7)所示,该方程同时包含了对流项与扩散项.
(7)
式中:x为速度;μ为介质黏度.虽然方程是非线性的,但是存在已知的解析解,可用于评估近似后的数值解,其解析解为
x(t,z)={0.1exp[-0.05(z-0.5+
4.95t)/μ]+0.5exp[-0.25(z-0.5+
0.75t)/μ]+exp[-0.5(z-
0.375)/μ]}/{exp[-0.05(z-0.5+
4.95t)/μ]+exp[-0.25(z-0.5+
0.75t)/μ]+exp[-0.5(z-0.375)/μ]}.
(8)
2.2 仿真分析
在MATLAB软件工具下编写程序进行仿真实验,再根据所得图像进行分析.其中μ=0.001;t=0,0.1,0.2,…,1,单位为min;网格数n=201;解析解输出图用虚线显示,线上求解法近似格式用实线显示.先对式(7)中的二阶偏微分项采用五点中心格式进行离散近似,再对一阶偏微分项分别进行五点偏心逆风格式近似、两点逆风格式近似、三点逆风格式近似和七点中心格式近似,所得图像分别如图1~图4所示.
图1中实线与虚线的贴合度十分完美,即数值解与解析解非常接近,表明五点偏心逆风格式对一阶偏微分项有非常好的离散效果.图2中显示一阶偏微分项由两点逆风格式近似后陡区域附近表现出波动现象(即解不稳定),不适合求解对流为主的问题.采用三点逆风格式近似一阶偏微分项的图像如图3所示.与解析解相比较,三点逆风格式近似对非物理振荡有比较好的抑制作用,但是陡区域不能完全贴合解析解,有一定误差,且在陡区的中部和后区的底部有一定振荡.最后观察图4,七点中心格式近似后的图像前中后部的陡区和底线与解析解都贴合较好,但是陡区的顶部都存在振荡,且在中后部的振荡幅度和频率更为明显.

图1 五点偏心逆风格式近似一阶偏微分项与解析解对比Fig.1 Contrast of five-point biased upwind approximate first-order partial differential terms and analytical solu tions
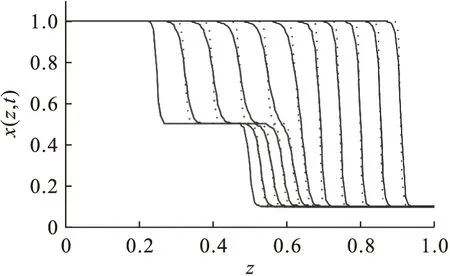
图2 两点逆风格式近似一阶偏微分项与解析解对比Fig.2 Contrast of two-point upwind approximate first-order partial differential terms and analytical solutions
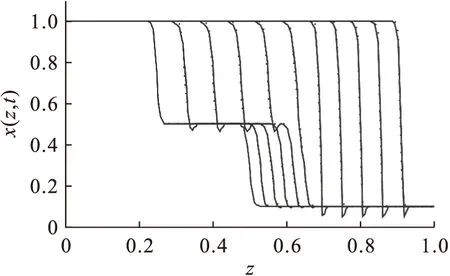
图3 三点逆风格式近似一阶偏微分项与解析解对比Fig.3 Contrast of three-point upwind approximate first-order partial differential terms and analytical solutions
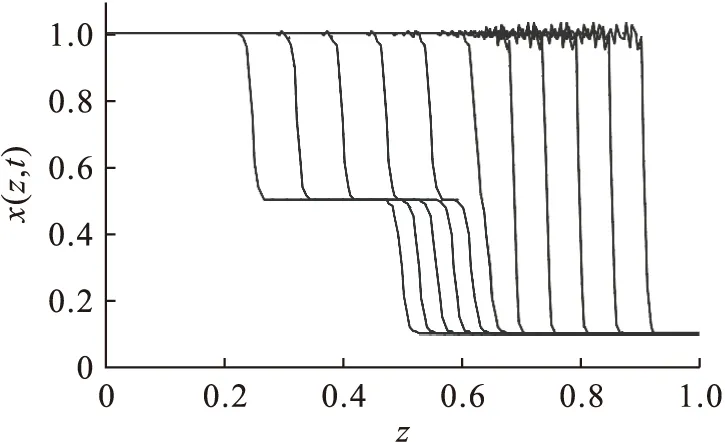
图4 七点中心格式近似一阶偏微分项与解析解对比Fig.4 Contrast of seven-point centered approximate first-order partial differential terms and analytical solutions
对式(7)中的一阶偏微分项给定五点偏心逆风格式进行离散近似,再对二阶偏微分项分别进行五点中心格式近似、两点逆风格式近似、三点逆风格式近似,其中五点中心格式近似后图像仍为图1,其余两种格式所得图像分别如图5、图6所示.
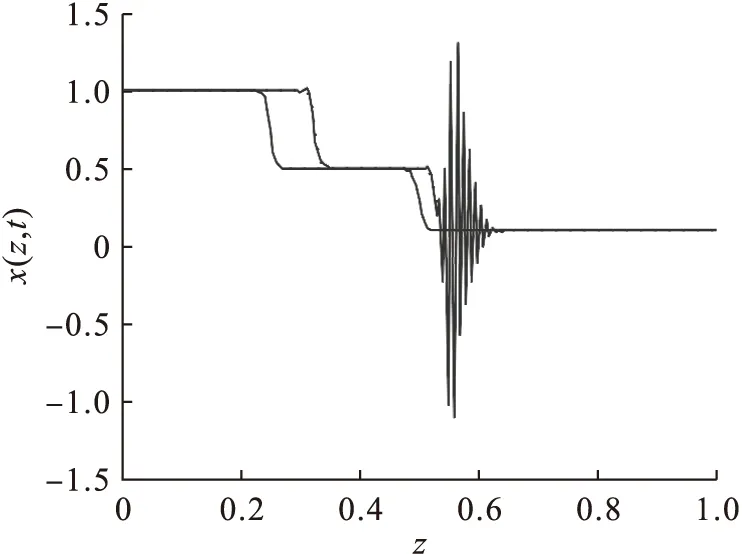
图5 两点逆风格式近似二阶偏微分项与解析解对比Fig.5 Contrast of two-point upwind approximate second-orderpartial differential terms and analytical solutions

图6 三点逆风格式近似二阶偏微分项与解析解对比Fig.6 Contrast of three-point upwind approximate second-order partial differential terms and analytical solutions
结合图像可以看出:将两点逆风格式用于近似二阶微分项所得的方程曲线与解析解相差很大,仅有陡区部分贴合,图像中部产生了巨大的振荡;三点逆风格式方法近似二阶偏微分项后的图像产生了非常大的偏差,从图6中已看不到解析解的图像.故可推测说明带有逆风格式的近似方法不适用于近似二阶微分项.
综上,在给定条件下通过对比几种近似一维Burgers方程偏微分项的方法,其中采用五点偏心逆风格式近似一阶偏微分项、五点中心格式近似二阶偏微分项后的曲线与解析解的曲线总体贴合度最好,误差最小.进而可以将其推广到其他领域,在对方程的偏微分项进行近似的时候,采取此种格式能取得更理想的效果.
3 MOL在化工过程中的应用
化工过程常常用偏微分方程组形式来表示,方程除了时间变量还存在空间自变量,此时若要对反应过程进行动态分析,方程组求解则要应用到MOL思想.其中苯加氢的三区管式固定床反应器的动力学方程组则是一个典型的偏微分方程组,该模型包括苯和噻吩的物料平衡方程、能量平衡方程以及考虑催化剂失活的方程,形式如式(9)~式(12)所示.
(9)
(10)
(11)
(12)
式中:DT为噻吩扩散系数;cT为噻吩的浓度;DB为苯扩散系数;cB为苯浓度;λeff为床导热性系数;R为反应器内半径;v为气体速度;ΔH为焓变;ρc为催化剂系数;ε为床空隙分数;ρG为气体密度;α为壁传热系数;rT为噻吩吸附率;rB为加氢率;T为温度.
根据以上结论验证该动力学模型,以五点偏心逆风格式近似方程一阶偏微分项,五点中心格式近似方程二阶偏微分项,所得反应器内部的温度分布曲线如图7所示.将图7作为标准图像.
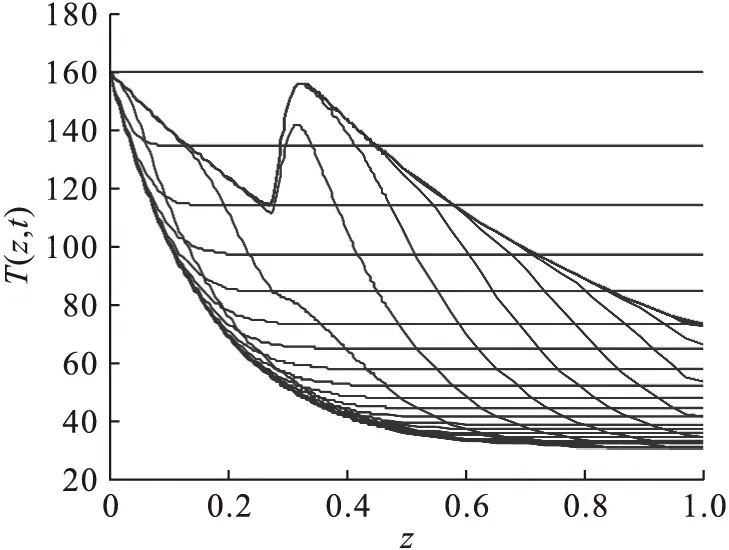
图7 标准格式近似图Fig.7 Standard format approximation
先保持用五点中心格式近似二阶微分项,对一阶微分项采用七点中心格式近似,所得反应器内部的温度分布图像如图8所示.与标准图像对比可以看出图8与标准图像有很大偏差.由于巨大振荡导致图像中后部偏离标准图像特别大,产生了误差.再将一阶偏微分项用五点偏心逆风格式近似,对二阶微分项则采用三点逆风格式近似,所得反应器内部的温度分布图像如图9所示.
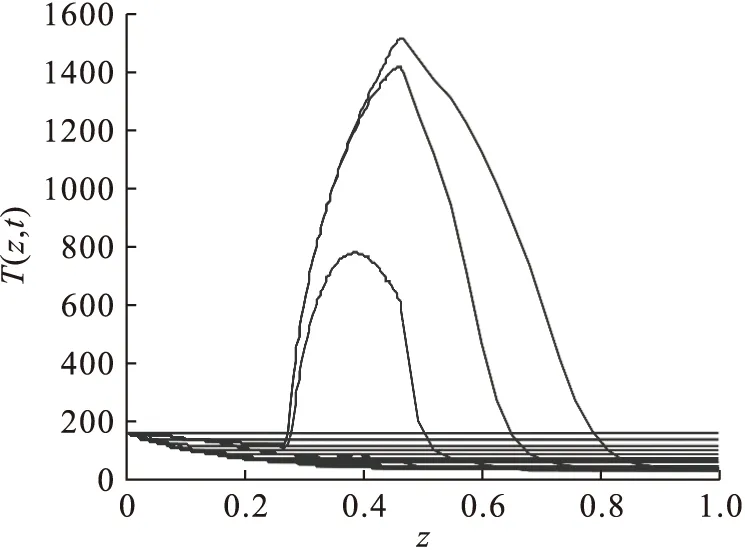
图8 七点中心格式近似一阶偏微分项Fig.8 Seven-point centered approximate first-order partial differential term
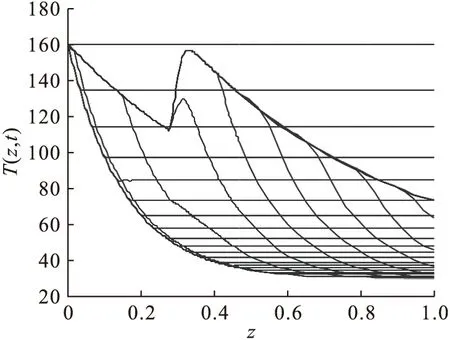
图9 三点逆风格式近似二阶偏微分项Fig.9 Three-point upwind approximate second-order partial differential term
与标准图像对比分析可知偏心逆风格式近似二阶偏微分项后图像曲线单薄,且上部陡区振荡明显,中部下凹曲线与标准图像相比误差也较大.
4 结 论
通过运用线上求解法思想,在给定条件下对比几种近似一维Burgers方程偏微分项的方法,得知以五点偏心逆风格式近似一阶偏微分项、五点中心格式近似二阶偏微分项所得曲线具有最理想的效果,并采用苯加氢管式固定床反应器这一典型化工过程进行仿真研究,验证了此推论的可靠性.

