无胶结粗粒土结构强度及量化指标分析

王 洋， 魏玉峰， 黄 鑫， 贺琮栖， 梁 彭

(成都理工大学 地质灾害防治与地质环境保护国家重点实验室， 四川 成都 610059)

1 研究背景

土体结构是指土体内各个组分在空间上的存在形式，是影响土体力学参数及属性的重要因素[1]，土体结构性研究在学科领域中一直是极其重要的研究方向。在粗粒土结构特性最新研究方面，郭万里等[2]总结了国内外粗粒土在现阶段的研究进展，并结合现有研究对粗粒土有关问题及研究方向提出了建议与展望。Li等[3]利用计算机断层扫描技术获得了三轴土石混合体试样中砾石的形状和位置，基于计算机断层图像，通过图像二值化、去噪和界面检测等数字图像处理技术，重建了三轴试样的典型纵剖面，建立了土体与砾石界面的线框模型。李海洋[4]利用CT技术对钙质砂的三维形状和孔隙进行了描述和量化，量化的指标包括孔隙率、扁平率、凹凸度、孔隙分维、伸长率和球度。在结构性指标描述方面，主要采用球度、光滑度、规则系数等指标描述颗粒形状[5]；以颗粒大小、形态、咬合、搭接等指标描述粗粒土排列特征[6-7]；根据接触面积、孔隙比变化、碰撞破碎等因素分析颗粒接触特征[8]。

土体结构性研究的最终目的就是要评价结构性对宏观力学性质的影响。卫振海等[9]通过对已有的土体模型进行分析,利用随机均匀网状颗粒链，得到了类似于剑桥强度模型的帽子模型；沈珠江[10-11]考虑结构性的数学力学模型在细粒土方面取得了丰硕成果，建立了破损力学模型和二元介质模型；王占军等[12]建立了考虑塑性流动方向和荷载方向的弹塑性本构模型；李吴刚等[13]通过结构性因子表征土的结构性，并利用修正剑桥模型建立了考虑土结构性的本构模型。在土颗粒形态指标对抗剪强度的影响方面，李远征等[14]利用室内直剪试验得出粗粒土黏聚力和内摩擦角与颗粒球度在一定范围呈现反比关系的结论。王勇[15]探究了黄土的结构性与抗剪强度之间的关系。而无胶结粗粒土方面鲜有类似的研究成果。

以上对于结构性的定量描述主要依据统计学、数学和物理学等方面的基本原理进行指标间关联影响的分析。针对一般粗粒土的研究还处于起步阶段。刘汉龙等[16]在综述文章的展望中提出，“粗粒土初始结构性”是土力学未来需要深入研究的内容；王光进等[17]认为土体初始结构是一个困难但值得深入研究的科学问题；魏玉峰等[18]通过试验对比了粗粒土原位状态与扰动状态的强度，揭示了粗粒土初始结构对土体抗剪强度的强弱具有直接的影响。当土体在受荷载作用进行剪切时，其内部结构的变化可分为两个阶段：第1阶段，荷载施加初期，初始结构并未破坏，在抵抗荷载过程中发挥着结构强度，结构的变化主要表现为初始结构的自适应调整；第2阶段，当荷载达到或超过土体原有的结构强度时，初始结构破坏，颗粒发生位移或错动，形成新的结构并最终趋于稳定。其中第1阶段在剪切过程中所抵抗的剪应力称为土体的初始结构强度。因而粗粒土强度的初始结构效应对抗剪强度的影响研究是极其重要的方向。

本文通过可视化直剪仪研究土体宏观抗剪强度中第1阶段所抵抗的剪应力数值，即初始结构所抵抗的剪应力数值。并从粗粒土颗粒形态，颗粒排列以及接触关系等指标进行量化分析。研究粗粒土初始结构的变化前后其各个量值指标的变化情况。采用层次分析法(analytical hierarchy process, AHP)以及熵权法来分析这3层指标对粗粒土抗剪强度的初始结构强度的影响强弱。揭示了粗粒土剪切过程中各个指标对粗粒土强度的初始结构效应的影响强弱以及初始结构的临界量值大小。

2 无胶结粗粒土初始结构强度探究

2.1 粗粒土结构强度分析

上述中当土体在受荷载作用进行剪切时，其内部结构的变化可分为两个阶段，其中第1阶段所抵抗的剪应力称为土体强度的结构临界强度，当剪应力小于临界强度时，颗粒之间随着剪应力的增加逐渐紧密，空隙率减小，发生剪缩现象；当剪应力大于临界强度时，随着剪应力的继续增加，颗粒将会发生明显的偏转及错动，颗粒的初始结构发生变化，形成新的结构并趋于稳定，直至颗粒失稳破碎。

将颗粒抗剪强度的初始结构变化点定义为颗粒整体出现明显错动及个别颗粒出现破碎或偏移的临界点。该临界点对应的剪应力值为粗粒土抗剪强度的初始结构效应临界量值，即粗粒土抗剪强度的临界强度。为了定性表达抗剪临界强度，通过大量可视化直剪试验来观测粗粒土初始结构变化点的形态。在剪切过程中只要出现颗粒连接破坏，即颗粒破碎或者偏转，则颗粒达到其临界强度。但是考虑到有些颗粒的连接变形在变形很大时，颗粒连接并没有发生破坏或偏转，但是其变形量发生了很大变化，因此这时以颗粒连接变形发生明显变化作为其抗剪强度临界限值(如图1所示)。

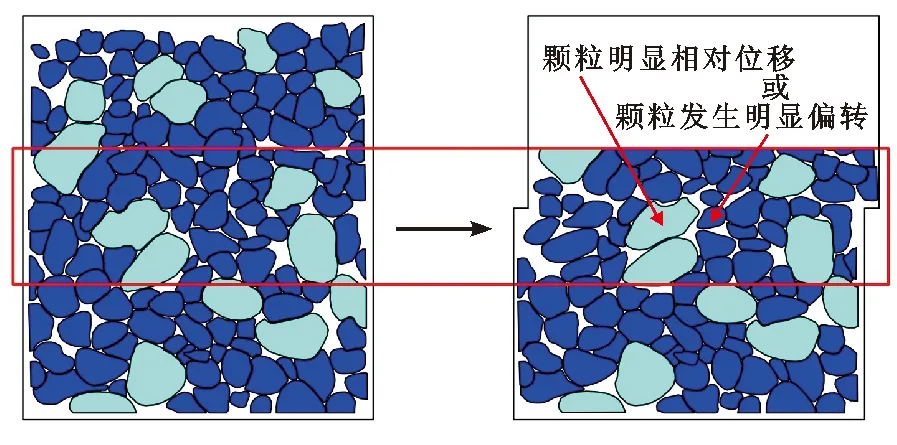
图1 土体颗粒初始结构变动点示意图

2.2 试验设计及结果

为了研究土体初始结构抵抗剪应力的临界值的影响因素，文章采用中型直剪试验仪，对剪切盒加以改装，设计出可视化的剪切盒。并使用数码相机在剪切过程中对土体的初始结构变化进行有效的实时观测，中型直剪仪结构如图2所示。

图2 中型直剪仪结构示意图

为将结构强度进行量化，提前通过试验发现，颗粒相对位移达到出现残余强度变形量的15%时，符合上述定义中的颗粒连接变形发生变化。后续实验将此量值作为颗粒初始结构变化点。为了更好地观察其剪切过程中结构的变化，防止因试验数据过少带来的误差，试验选取直径范围在10～40 mm的粗骨料，不同配比颗粒分别在不同正应力的情况下共进行32组试验，并通过标准筛对颗粒进行区分。为了使试验结果具有对比性，排除正应力的影响以及试验的偶然误差，其配比情况如表1所示。

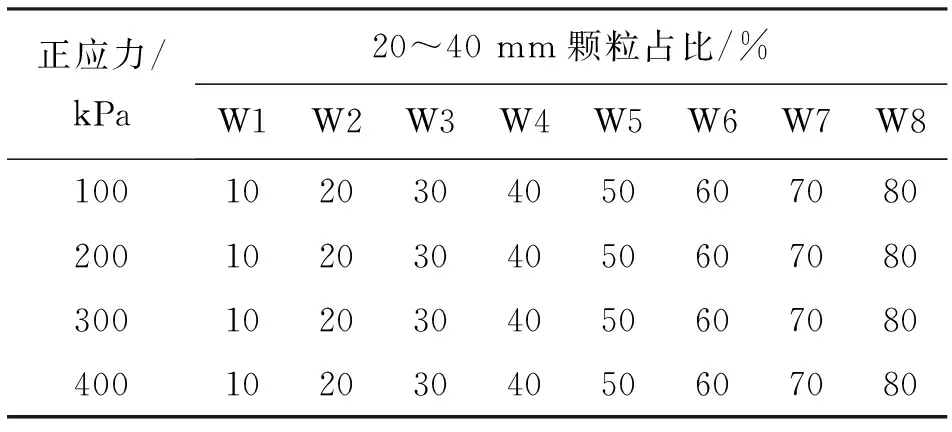
表1 试验土体颗粒配比情况

注：配比颗粒除20～40 mm外均为10～20 mm；W1～ W8为组次编号。

使配置好的粗粒土分别在100，200，300，400 kPa的正应力下进行剪切，在试验过程中通过可视化装置观察粗粒土的剪切过程，在试验结束后反复观察录像机并结合试验数据中的应变突变点，得到粗粒土抗剪强度的初始结构临界量值的范围。通过记录的试验数据绘制其应力-应变曲线图，并标出初始结构变化点。不同正应力下各组次颗粒配比土体的应力-应变曲线如图3所示。

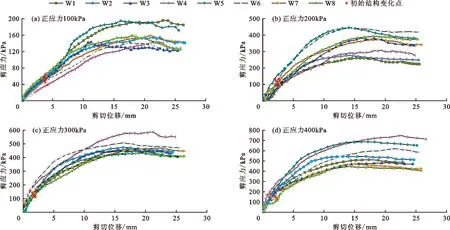
图3 不同正应力下各组次颗粒配比土体的应力-应变曲线

根据不同正应力下不同配比的颗粒在试验过程中的数据及其应力-应变曲线，将各个试验组次的峰值强度、结构临界强度及其临界强度占比情况汇总于表2。

分析图3和表2可知，当20～40 mm颗粒占比较大时，随着正应力的逐级递增，土体的峰值应力近乎均匀增加；当20～40 mm颗粒占比较小且当正应力增加至300 kPa时，大颗粒之间的接触增强，峰值应力迅速增大，骨架效应明显提升。整体上来看，当20～40 mm颗粒占比较大时，粗粒土的峰值抗剪强度较大，其结构强度也相应增大。结合32组试验综合求得颗粒结构临界强度占其峰值抗剪强度的31.09%，即颗粒结构所抵抗的剪应力约占整体抗剪强度的1/3，这对于初始结构所抵抗的剪应力值大小的影响因素探究是十分有意义的。该临界值对于粗粒土垫层地基以及高土石坝中用粗粒土填筑具有指导意义。例如在饱和黄土地基上修建高层建筑工程时，常采用粗粒土垫层进行地基处理，在一些粗粒土垫层的路基中，颗粒主要受剪应力的影响，而当剪应力超过其临界强度时，个别颗粒会发生偏转错动，其上部结构会发生开裂以及不均匀沉降。

表2 初始结构抗剪强度临界值及其占比

3 土体颗粒特征的量化分析

为探究颗粒本身形态、样貌，颗粒排列，颗粒接触这些颗粒内在因素对颗粒结构强度的影响权重大小，本文对这些内在因素进行量化，并通过统计学方法对各个量化指标进行分析。

3.1 颗粒特征量化指标

3.1.1 颗粒形态 土体颗粒形态的差异是粗粒土初始结构的量化分析中一个重要的影响因素。关于颗粒形态的表征指标中，本文以粗糙度[19]、棱角度[20-21]以及整体轮廓系数[20]3项指标来描述颗粒形态，其计算原理如图4所示。

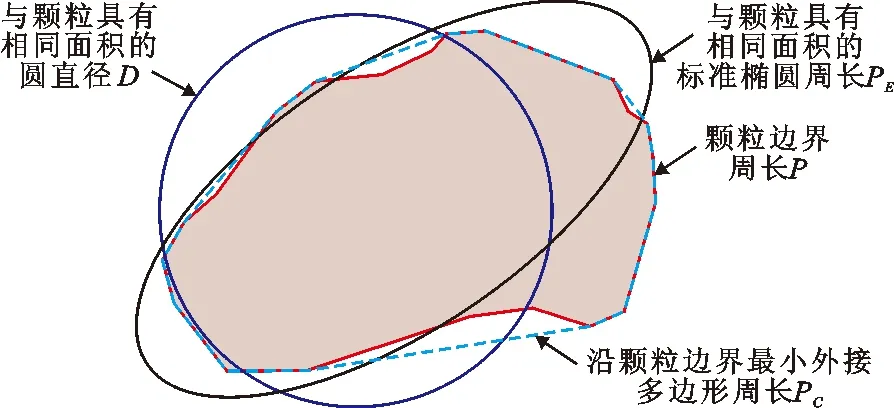
图4 颗粒形态各量化指标计算原理示意图

粗糙度r反映了颗粒表面微纹理结构、不规则性以及边界曲线起伏的变化程度等。其公式表达为：

(1)

式中：P为颗粒边界上连续像素的距离之和，即周长；PC为沿颗粒边界的最小外接多边形周长。

棱角度Ag定义为颗粒最小外接多边形周长PC与等效面积椭圆周长PE之比。棱角度重点在于描述颗粒表面棱角的突出度或磨圆程度，其公式表达为：

(2)

式中：Ag越接近于1，则其表面越圆滑，棱角越不明显。数值越大时则反之。

整体轮廓系数α定义为等效面积圆周长与颗粒自身周长之比。在面积一定的情况下，整体形状越偏离圆形，则α值越小，该系数描述了轮廓全局面貌。公式表达为：

(3)

式中：D为与颗粒具有相同面积的圆直径；P为颗粒边界上连续像素的距离之和。

参考相关研究结果[22-23]，本文颗粒形态的量化分析通过3个层次的3项指标来表征。该3项指标具有很好的区分度，作为主要参数来表征粗粒土抗剪强度的初始结构效应是合理的。

3.1.2 颗粒排列 颗粒排列对粗粒土力学特性具有重要影响。由于粗粒土多为单粒结构，互相之间粘结性较小。因此选择用颗粒的定向性来对颗粒排列进行表述。单粒粗颗粒土一般具有明显的长短轴方向，长轴即为颗粒间距离最远的两点的连线。而颗粒长轴与坐标轴横向的夹角为主定向角，如图5所示。

图5 颗粒长轴定向性示意图

定向角每10°为一个区间，共18个区间。此方法可统计出颗粒排列的方向，用以研究颗粒体系的定向分布情况。为了更好地反映颗粒单元体排列的这种定向性[24]，在现代信息系统中引入概率熵这一指标，即：

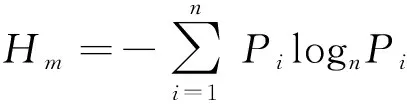
(4)

式中：Hm为颗粒单元体排列的概率熵；Pi为颗粒在某一方位区间中呈现的概率；n为颗粒排列方向的方位区数，n=18。

显而易见，Hm的取值在[0,1]区间，Hm反映了颗粒的定向性，其值越大表明颗粒的定向性越差，反之越好。因此选用概率熵来表征颗粒排列的有序性是合理的。

3.1.3 颗粒接触关系 由于粗粒土内部组成颗粒的尺寸不一，颗粒表面特征具有复杂的多样性。其粒间接触方式主要有以下3种：点接触，即颗粒之间以“点-点”的形式相互接触；面接触，即颗粒之间以“面-面”的形式相互接触；凹凸接触，即颗粒之间以“凹凸衔接”的形式相互接触。3种接触方式如图6所示。

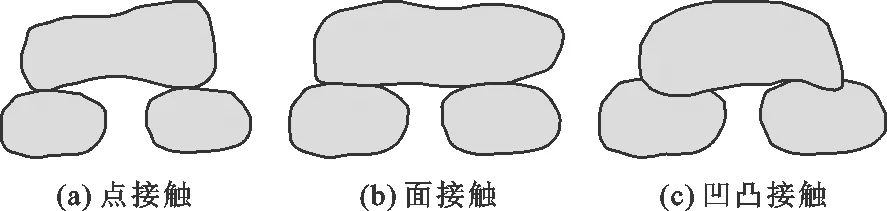
图6 3种颗粒接触方式示意图

颗粒接触关系采用配位数Cn这一量化指标进行描述，该指标即为平均接触颗粒数目，是对颗粒粒径、级配、孔隙比等参数的综合量化指标，反映了粗粒土的接触形式及密实程度。

(5)

式中：Nd为颗粒总数目；nc(d)为d颗粒的接触数目。

3.2 初始结构前后颗粒量化指标变化及分析

为了确定无胶结粗粒土的各量化指标对其初始结构临界剪应力值的影响权重，通过图像处理技术(如图7所示)提取颗粒结构状况，对各个量化指标进行计算。

图7 无胶结粗颗粒图像处理平面示意图

通过将处理后的颗粒图像平面图导入Image-pro plus软件，计算出颗粒面积、周长、等效椭圆周长、外界多边形周长以及定向角等所需的参数，并以平面颗粒的各量化参数代替整体颗粒相应的参数值。

将32组试验经过Image-pro plus软件计算后再进行整合计算，为消除不同正应力对各个指标权重的影响，将不同正应力同一颗粒级配的试验组别定为同组，对各个指标取其平均值进行分析，共分为8组(Y1～Y8)。各组次颗粒的各初始平均量化指标如表3所示。

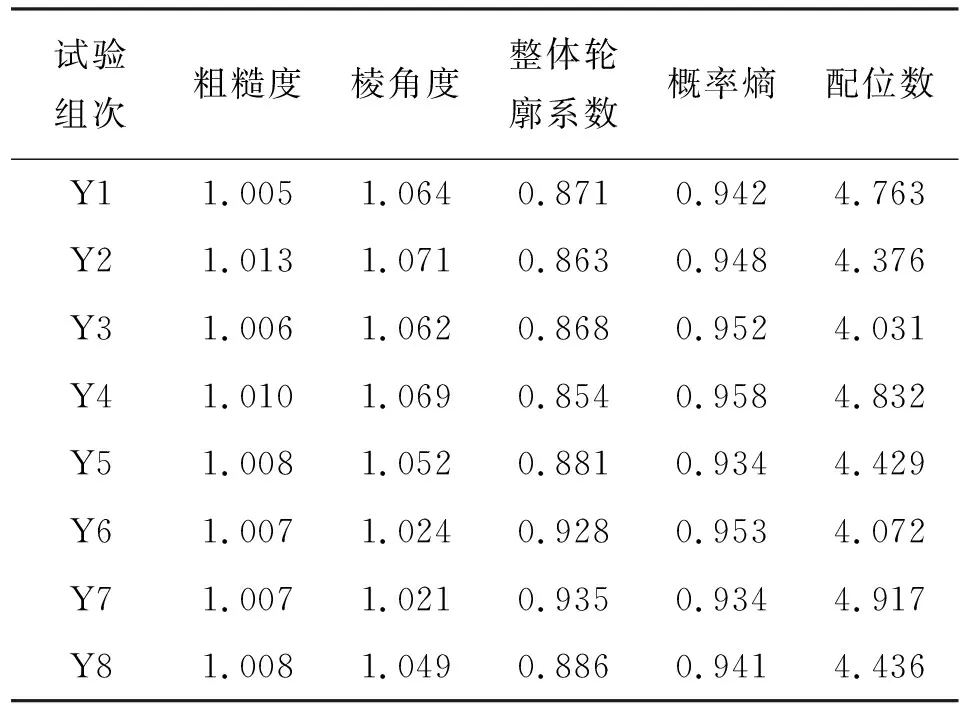
表3 初始结构变化点前各试验组次颗粒量化指标汇总

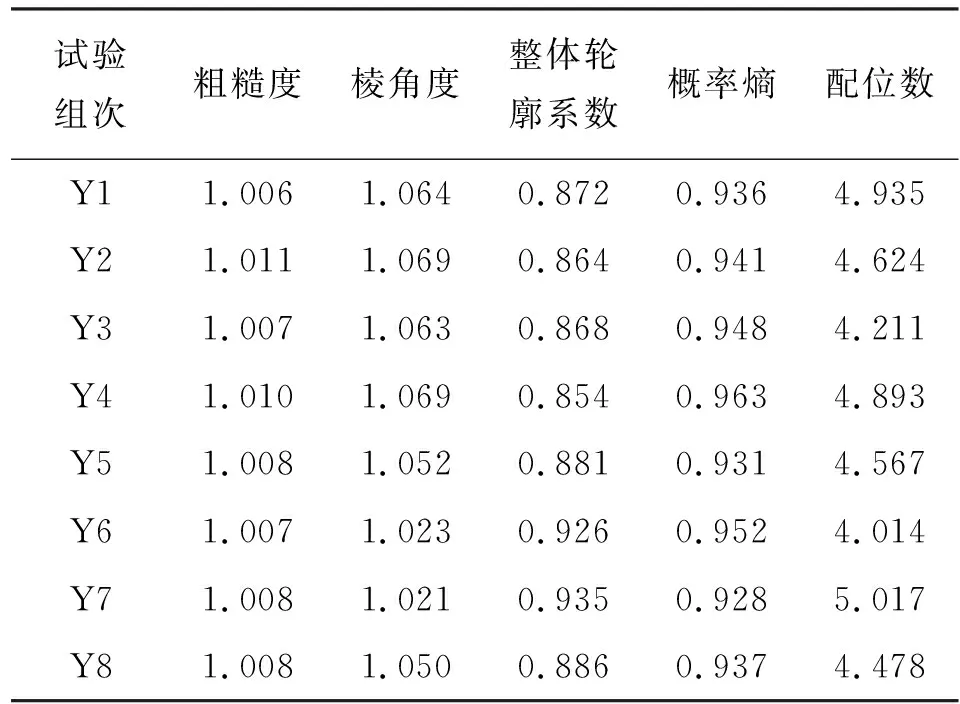
当颗粒在剪切过程中经过初始结构变化点时，通过图像处理技术(图8所示)提取各个颗粒指标，32组试验按上文分组，计算8组试验各指标的平均值，结果如表4所示。

图8 初始结构变化点后图像处理平面示意图表4 初始结构变化点后各试验组次颗粒量化指标汇总

试验组次粗糙度棱角度整体轮廓系数概率熵配位数Y11.0061.0640.8720.9364.935Y21.0111.0690.8640.9414.624Y31.0071.0630.8680.9484.211Y41.0101.0690.8540.9634.893Y51.0081.0520.8810.9314.567Y61.0071.0230.9260.9524.014Y71.0081.0210.9350.9285.017Y81.0081.0500.8860.9374.478

通过对比分析表3和4中初始结构变化点前后颗粒各个量化指标的变化发现，在初始结构变化点之后，颗粒接触关系变化最为显著，除Y6组次之外的其他组次颗粒配位数均呈现增加的趋势。这是由于颗粒初始结构变化之后颗粒重新排列，颗粒之间接触得更加紧密，导致颗粒配位数增加。而颗粒排列中的概率熵除Y4组次之外的其他组次在初始结构变化后总体呈现减小的趋势，这是因为在剪切的作用下，剪切带附近的大多数颗粒的长轴处于水平位置，与之前颗粒排列相比定向性更加统一，致使概率熵总体呈现减小的趋势。而颗粒量化指标中的粗糙度、棱角度、整体轮廓系数是基于颗粒本身形态的指标，在较低正应力下初始结构变化后大部分颗粒并没有破碎，颗粒形态几乎没有发生变化，因此颗粒形态指标没有呈现规律性的变化趋势，与颗粒初始状态的形态指标几乎无异。但在高压下剪切带附近颗粒发生破碎，颗粒形态指标将会发生变化，其中由于破碎颗粒棱角较为突出，故棱角度的变化最大。

颗粒排列以及颗粒接触关系是影响初始结构变化的主要指标，在剪切带附近的颗粒经过初始结构变化之后，颗粒排列及接触关系变化程度最大。在个别组次试验中颗粒形态指标也存在变化，这主要是因为剪切带附近的颗粒产生翻转和位移，导致颗粒在对外的可视化平面中发生变化，而本试验中采用平面颗粒结构代替整体颗粒结构，故颗粒形态指标发生了微弱的变化。

4 基于AHP-熵权法的量化指标权重研究

4.1 量化指标分析方法

由于各个量化指标之间是相关联的，用控制变量的试验研究方法控制粗粒土各量化指标难以实现。因此为了更好地确定粗粒土各量化指标对初始结构临界剪应力量值的影响强弱，本文采取层次分析法(AHP)和熵权法共同来确定各因素的权重。

4.1.1 层次分析法(AHP) 层次分析法是将n个因素排列成一个n阶矩阵，将各个因素的重要性进行比较的一种方法[25]。影响粗粒土初始结构抗剪强度变化的因素共5个。用集合表示为：U={u1,u2,u3,u4,u5}，其中u1为颗粒粗糙度、u2为颗粒棱角度、u3为整体轮廓系数、u4为颗粒排列量化指标中的概率熵、u5为颗粒接触关系量化指标中的配位数。

通过1-9比率标度法利用以上5种因素构造判断矩阵，通过将每2种因素进行相互比较，得出以下判断矩阵：

对判断矩阵特征根及特征向量进行计算如下。

①计算判断矩阵每行元素的乘积Wi：

(6)

则W1=0.083，W2=0.083，W3=6，W4=0.333，W5=72。

②计算Wi的5次方根Mi：

(7)

则M1=0.608，M2=0.608，M3=1.431，M4=0.803,M5=2.352。

(8)

则特征向量A为：

A=(0.105,0.105,0.247,0.138,0.405)T

则最大特征根为：

(9)

④一致性检验计算：

问云梦，看见我的书了吗？云梦说没看见啊。再问丈母娘，看见我的书了吗？老人说，是书皮上印一把生锈的大铁刀的那本吗？呼伦心里咣当一声，暗叫，坏菜了！

(10)

查随机性指标CR数值表可知，当n=5时，CR=1.12，则：

上式表明判断矩阵的一致性达到要求，因此特征向量A的各个分量可以作为相应评价因素的权重系数即A=(0.105,0.105,0.247,0.138,0.045)T。

4.1.2 熵权法 熵权法是将指标变异程度作为依据，确定各个指标权重。将试验颗粒量化指标数据(表3)根据下式进行数据标准化。

(11)

其中Xi={x1,x2,…,x8}对应的每个指标的8组数据。标准化后的值为Y1,Y2,…,Y5(表5)。

由信息熵的定义，将表5中标准化后的数据根据公式(12)得出信息熵。

(12)

得出信息熵后通过公式(13)计算各指标的权重，计算结果列于表6。

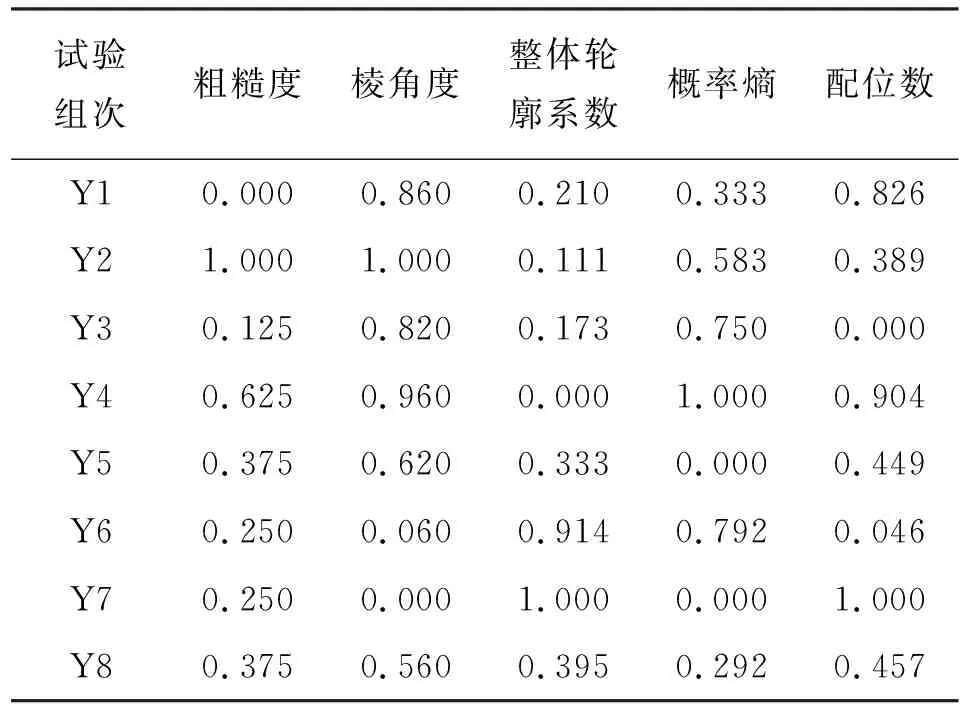
表5 量化指标标准化结果

(13)

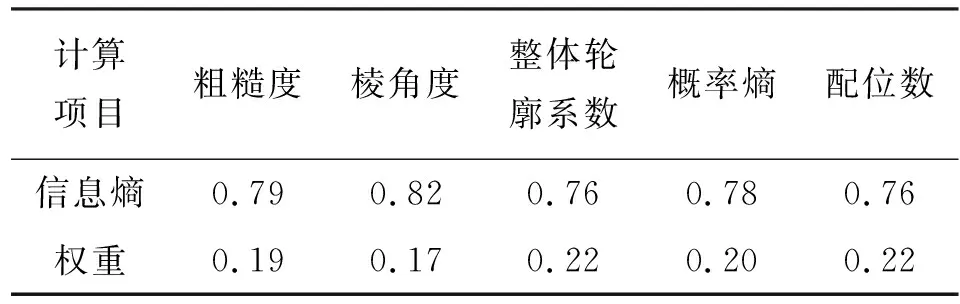
表6 量化指标信息熵及权重

(14)

式中：Vi为层次分析法确定的权重；Yi为熵权法确定的权重。

将两种方法确定的权重结果代入公式(14)得出最终权重系数，即粗粒土各量化指标对初始结构临界剪应力量值的影响权重依次为(0.095 5，0.085 5，0.260 2，0.132 2，0.426 6)，即粗糙度、棱角度、整体轮廓系数、概率熵和配位数对颗粒结构强度的权重分别为9.55%、8.55%、26.02%、13.22%和42.66%。

4.2 量化指标权重分析

由上述权重计算结果可知，配位数对颗粒抗剪强度的初始结构临界剪应力值的影响最大，其权重达到了42.66%。配位数所对应的是颗粒接触关系，在颗粒抵抗剪应力的过程中，颗粒接触关系发挥了比较重要的作用，如图6所示的3种颗粒接触方式，当颗粒之间为凹凸接触时对抵抗剪应力的贡献最大，而当颗粒之间为点接触时对抵抗剪应力的贡献较小，故接触关系是抵抗剪应力的一个重要指标。与其他量化指标相比，颗粒接触关系对抵抗剪应力的影响最大，是符合实际的。在工程上利用强夯法处理粗粒土地基，其目的也是使粗粒土孔隙比降低，接触更加紧密，以此来提高粗粒土的抗剪强度。其次是整体轮廓系数和概率熵指标，整体轮廓系数从整体上描述了轮廓形貌特征，其权重系数为26.02%。概率熵则对应着颗粒排列的有序性，其权重系数为13.22%。

由于各个指标之间是相关联的。因此选用了AHP-熵权法对各个量化指标的权重进行研究。该方法得到的权重系数结果揭示了颗粒特征指标对颗粒抵抗剪应力的贡献强弱。在采用粗粒土垫层时为了使垫层有更高的承载能力和抗剪能力，可以选用级配良好的粗粒土并使颗粒接触方式更多的为凹凸型接触，同时选用整体轮廓系数较好的颗粒，可以使粗粒土的初始结构强度更加稳定。

5 讨 论

本文研究内容与王光进等[17]研究的粗粒土初始架构不同，本文详细阐述了粗粒土结构强度的定义以及粗粒土量化指标对结构强度的影响，对于构建真实的粗粒土初始结构模型提供了思路。同时魏玉峰等[18]的研究中通过试验对比，提出了粗粒土结构性对抗剪强度具有一定影响的结论。基于此，本文着重研究粗粒土结构强度的占比，根据可视化直剪仪试验结果，确定了粗粒土初始结构所抵抗的剪应力约为峰值抗剪强度的1/3，并对粗粒土常见的量化指标进行分析，通过统计学方法分析各个量化指标对结构强度的影响权重。

由于可视化直剪仪的局限性，只能用一个平面结构来代替颗粒内部整体的结构变化情况，对粗粒土结构量化指标的分析也只限于用观测到的二维平面代替，其颗粒内部变化情况还需进一步验证。在今后的研究中可以利用CT扫描技术及X射线计算机技术构建三维模型，对粗粒土结构性问题进行研究，分析剪切过程中颗粒内部的变化情况，构建完整的粗粒土初始结构模型。

6 结 论

本文依托可视化中型直剪试验对粗粒土初始结构临界值进行分析研究，分析了颗粒在剪切过程中的结构强度及其结构强度与峰值强度的比值，并对颗粒特征进行量化指标分析，通过层次分析法及熵权法对各量化指标对初始结构临界剪应力量值的影响权重进行计算，得到以下结论：

(1)对无胶结粗颗粒进行直剪时，颗粒结构强度占其峰值抗剪强度的31.09%，即颗粒结构所抵抗的剪应力约占整体抗剪强度的1/3。

(2)当颗粒在剪切经过结构临界强度即初始结构变化点时，通过各量化指标变化发现，颗粒的排列及接触特征变化最大，颗粒的形态几乎不发生改变。

(3)采用AHP-熵权法对颗粒形态、颗粒排列以及颗粒接触关系的各个量化指标进行分析计算，得出了各个量化指标对初始结构临界剪应力量值的影响权重。结果表明，颗粒接触关系对初始结构临界剪应力量值的影响最大，其权重占比为42.66%；其次为颗粒形态指标中的整体轮廓系数，其占比为26.02%。