多变量综合干旱指数在渭河流域的应用

朱悦璐, 张 阳

(南昌工程学院 水利与生态工程学院， 江西 南昌 330099)

1 研究背景

IPCC(International Panel on Climate Change)第五次报告指出[1]，随着二氧化碳排放量的增加，温室效应急剧加速，全球陆地干旱面积迅速扩大。据美国新泽西理工学院2021年9月最新公布研究结果显示[2]，过去20年间，在CO2排放、温室效应、区域干旱耦合作用下，地球的光度、反照率下降，反射至太空的可见光减少，导致地球吸收了更多的能量，从而进一步加剧了气候变化和全球变暖、变干的趋势。在这一背景下，我国干旱事件问题，尤其是西部地区黄土高原干旱易发区的干旱事件时空演变问题，成为近年来一个研究热点[3]。

干旱指数是研究干旱事件的有力工具，众多学者据此已有大量研究，王荣江等[4]基于SPI、SPEI、MCI等干旱指数，评价了四川省1987-2010年的干旱变化过程。甘肃农业大学资源与环境学院利用标准化降水蒸散发指数，结合干旱发生频率对黄土高原未来干旱事件进行预测，预测结果表明，在该地区，夏季干旱风险大于其他季节[5]。曲美慧等[6]基于连续无效降水指数对作物生长季干旱以及季节性干旱进行了识别，其结果与试验吻合。

上述研究成果已十分丰富，可以针对某一类型干旱作出诊断，但由于水文、气象、农业部门对干旱事件关注的侧重不同，导致各指数定义不同、划分方法不一，因此在很多情况下上述单变量干旱指数并不通用，亦不能相互比较[7]。事实上，即便针对一场特定的干旱事件，不同指数的评价结果也会存在显著差异。以最为常见的标准化降水指数(standardized precipitation index,SPI)和Palmer干旱指数(palmer drought severity index,PDSI)为例，SPI指数用Gamma分布来修正真实降雨的偏态分布，但同一地区，用于PDSI指数计算的土壤湿度往往不遵循这一分布，这必然导致二者对于同一干旱事件的判定结果不一致。因此，构建一种可用于不同时空尺度的综合干旱指数，成为研究者新的关注方向。在实际应用中，构建综合干旱指数的核心之一在于各单变量指数所占权重如何估算。已有很多学者对其方法做出初步尝试，包括组合权重法[8]、经验赋权法[9](例如某指数在某流域历史上多次判断效果较好，则该指数权重较高)、主成分分析法[10]、统计回归权重法[11]等。大量工程实践表明，这些方法在一定程度上能区分各指数权重，但由于选择上带有主观因素和偶然因素，对构建综合干旱指数的稳定性影响较大。

为解决上述问题，本研究以实测降雨、径流数据为基础，选择4种在研究领域广泛应用的单变量干旱指数，通过熵权法、模糊评价法、经验法三重赋权，构建可用于描述气象干旱和水文干旱的综合干旱指数MHDI(meteorological and hydrological drought index)，并利用该指数，在我国西部地区典型流域——渭河流域进行应用，分别在渭河流域的5个子流域上讨论年代际、年际、年内等不同尺度的干旱变化规律，并对未来一段时间内流域的干旱趋势进行预测。该研究方案既避免了单一指数无法识别干旱事件全貌的问题，又减少了传统综合干旱指数在赋权上的不确定性，可作为我国西部地区干旱风险评价的一种补充。

2 数据来源与研究方法

2.1 区域概况及数据

渭河流域地处我国西部，是黄河一级支流，其地理坐标为东经106°18′～110°37′，北纬33°42′～37°20′，流域覆盖陕西、甘肃、宁夏3个省(区)，具有西北地区典型流域特征，各类干旱事件频发。泾河为渭河第一大支流、北洛河为渭河第二大支流，本研究将渭河流域分为渭河上游、渭河中游、渭河下游、泾河流域、北洛河流域共5个子流域，各子流域水系及水文站、气象站分布如图1所示。研究所用数据为图1所示的各站点1960-2010年的水文、气象实测资料。

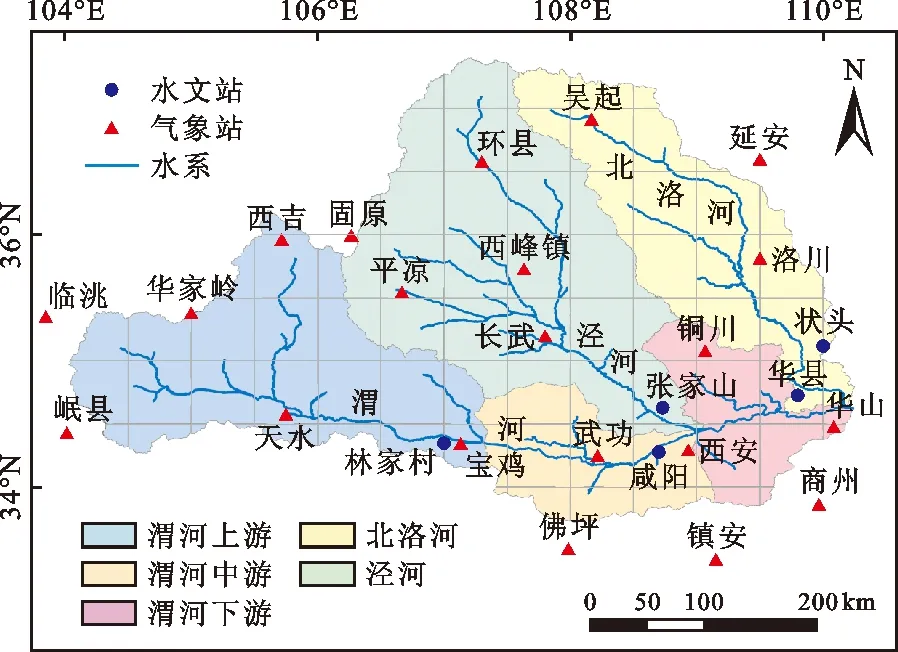
图1 渭河各子流域水系及水文站、气象站分布

2.2 研究方法

2.2.1 熵权法计算单变量指数权重 熵权法的核心为[12]：当某项指标值的差异性越大，则该指标在综合评价中所起的作用越大，反之该指标的作用越小。本研究选取降水距平百分率[13]、标准化降水指数SPI[14]、河道来水量距平百分率[15]、修正Palmer干旱指数PDSI[16]等4种常见干旱指数作为构建综合干旱指数的基础，按照传统干旱等级分类方法，将干旱状态划分为无旱、轻旱、中旱、重旱、特旱5个等级，如表1所示。

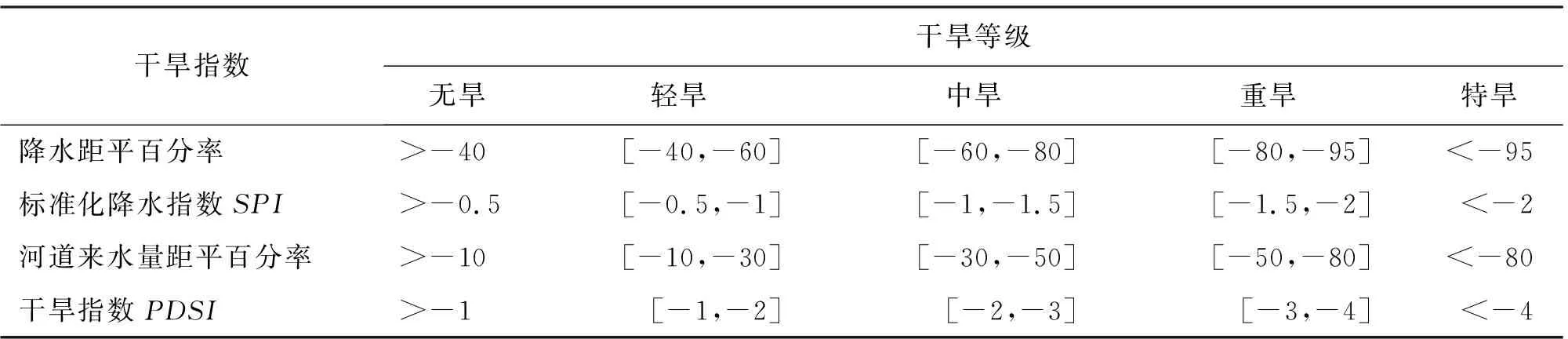
表1 干旱等级划分

根据表1，设干旱评价指标m=4，干旱评价等级n=5，则有原始矩阵X=(xij)m×n，矩阵中的元素xij以雷江群等[17]采用的“干旱等级区间-矩阵”转换方法生成，该方法认为矩阵第1列和最后1列分别对应表1中无旱和特旱所在列数据，其余各元素为各对应区间的均值，因而得出原始矩阵如下：

原始矩阵构建完毕后，采用以下步骤对各指标赋予权重。

(1)原始数据标准化。采用规范化方法[18]将原始矩阵X=(xij)m×n标准化，如式(1)所示；标准化后矩阵中每一个元素均为无量纲常数，该做法可消除不同干旱指数由于评判标准不同而不能相互比较的问题。

(1)

式中：rij为第j个评价对象在第i个评价指标上的标准值，且rij∈[0,1]。

rij的具体计算方法为：

rij=[xij-minj(xij)]/[maxj(xij)-minj(xij)]

(2)

式中：maxj(xij)、minj(xij)分别为原始矩阵第j列中的最大、最小值。

(2) 定义熵。在有m个评价指标，n个评价对象的评估问题中，第i个指标的熵定义为：

(3)

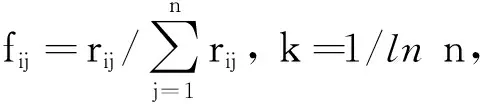
(3) 定义熵权。当定义了第i个指标的熵之后，第i个指标的熵权定义为：

(4)

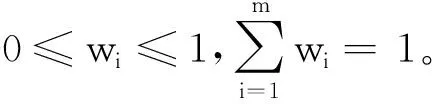
通过上述步骤(1)～(3)计算出各干旱指数权重，如表2所示。

表2 各干旱指数权重

2.2.2 模糊评价法计算隶属度权重 干旱指数对干旱等级的隶属程度即隶属度矩阵，也是该指标权重的一种形式。本研究采用模糊综合评价法[19-20]，结合实际算例简要介绍这一问题。应用文献[13]～[16]中传统单变量干旱指数计算方法，计算出2000年9月渭河流域中游降水距平百分率、SPI值、河道来水量距平百分率、PDSI值分别为-83.4、-1.7、-67.0、-3.3。以降水距平百分率计算结果-83.4为例，该值落在原始矩阵X对应的[-70，-87.5] 指标区间内。此时，按照文献[17]所用方法，降水距平百分率在x12、x13元素上对于干旱等级的隶属度为：

此时，原始矩阵第1行其余的3个元素，即x11、x14、x15均为0，则降水距平百分率对应的隶属度向量为α1=[0，0.235,0.765,0,0]。应用同样方法，计算其他3个干旱指数的隶属度向量，并构建隶属度矩阵K为：

将隶属度矩阵K与表2各指数权重按文献[21]中介绍的模糊综合法规则进行运算，求得权重隶属度矩阵W如下：

记权重隶属度矩阵每列之和为R=[0,0.059 6,0.631,0.107,0.201]，则矩阵R可综合反映各因素对不同干旱程度的影响。

2.2.3 经验赋权法计算MHDI设无旱、轻旱、中旱、重旱、特旱权重Bi分别为0、0.5、1、1.5、2(该权重为干旱等级本身的权重，与上文讨论的各干旱指数权重不是同一概念)，则最终2000年9月渭河流域中游综合干旱指数MHDI可表示为：

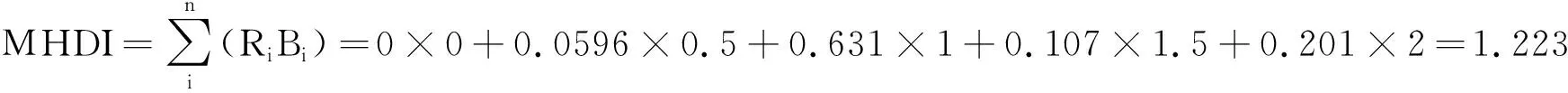
本研究以均值标准差法，并参考区域干旱等级标准[22]将MHDI值划分为5个等级，如表3所示，则上述算例中渭河中游2000年9月MHDI=1.223，属于严重干旱。

表3 综合干旱指标等级划分

重复上述熵权法、模糊评价法及经验法3个赋权步骤，即可求得研究流域及其各子流域月、季、年等不同尺度下的综合干旱指数MHDI。

3 结果与分析

3.1综合干旱指数验证

(1)年尺度下全流域典型干旱年份验证。为验证综合干旱指数MHDI的可靠性，本研究计算了1961-2010年渭河全流域年平均综合干旱指数(如图2所示)，并选取该历史时期渭河流域典型干旱年份1986、1995和1997年进行对比分析。

图2 1961-2010年渭河全流域年平均综合干旱指数变化趋势

由图2可以看出，1986、1995、1997 这3个年份的MHDI值分别为1.51、1.58、1.52，根据表3的综合干旱指数等级划分，上述3个年份可判定为极端干旱，该结论与历史资料相吻合，这表明本研究构建的MHDI指数在全流域年尺度上有较好的适用性，可以描述典型干旱事件。

(2)月尺度下子流域极端干旱事件验证。以1997年5月下旬至9月上旬陕西省高温干旱，尤其是关中地区严重高温干旱事件为例[23]，分别计算月尺度下渭河流域中游4种单变量干旱指数和综合干旱指数MHDI，计算结果及干旱事件识别效果如表4所示。

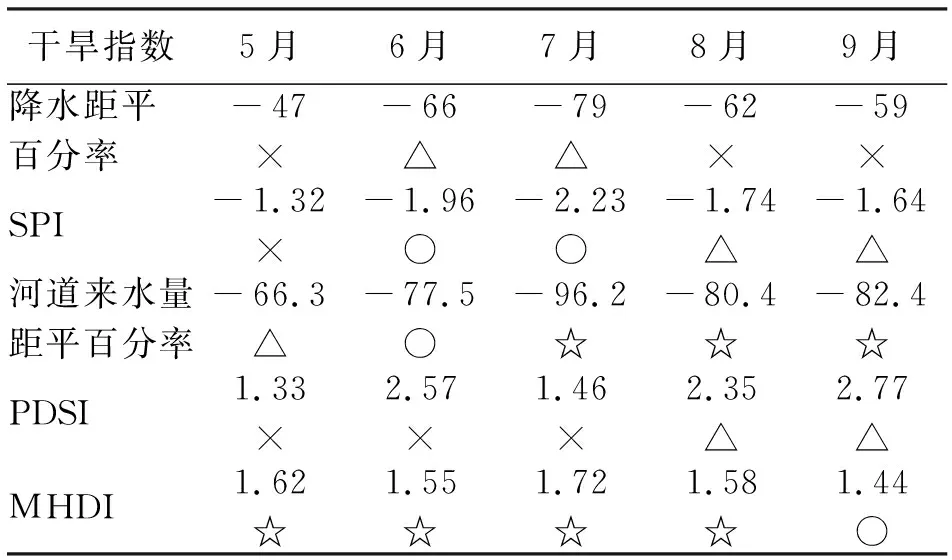
表4 1997年5-9月渭河流域中游各干旱指数计算值及

注：表中“☆”“○”“△”“×”依次表示识别效果为优、良、中、差。

由表4计算结果对照表1和表3干旱指数区间等级表可以明显看出，针对1997年陕西省及关中地区连续5个月的极端干旱，各单一干旱指数均不能完整识别该次事件，在单变量干旱指数中，识别效果最好的是河道来水量距平百分率，该指数与水文干旱关系最为密切，因此效果较好，而基于本文构建的综合干旱指数MHDI，除了9月份干旱末期判断效果稍差外，其余月份均较好地识别出了干旱事件。因此MHDI指数亦适用于描述极端干旱事件。

3.2研究区年代际干旱演化规律

计算1960-2010年研究区各子流域月MHDI值，并统计其间各子流域严重干旱和极端干旱发生的次数，统计结果如图3所示。

由图3可以看出，研究区各子流域干旱变化趋势在1960-2000年间整体上呈现波动上升趋势，20世纪90年代的MHDI均值达到最大，各子流域严重干旱、极端干旱平均出现次数达到40次，这表明在年代际尺度上，20世纪60-90年代流域有逐渐变干的趋势； 2000-2010年流域干旱程度恢复到70年代水平，表明流域干旱程度在21世纪初有所缓解。

图3 1960-2010年各年代研究区各子流域严重干旱和极端干旱发生的次数统计

3.3 研究区年际干旱演化规律

本研究采用M-K(Mann-Kendall)法[24]计算各子流域1960-2010年综合干旱指数MHDI年平均值的变化趋势，M-K检验法的计算过程及判断标准见参考文献[24]。各子流域年际干旱变化趋势计算结果如表5所示。

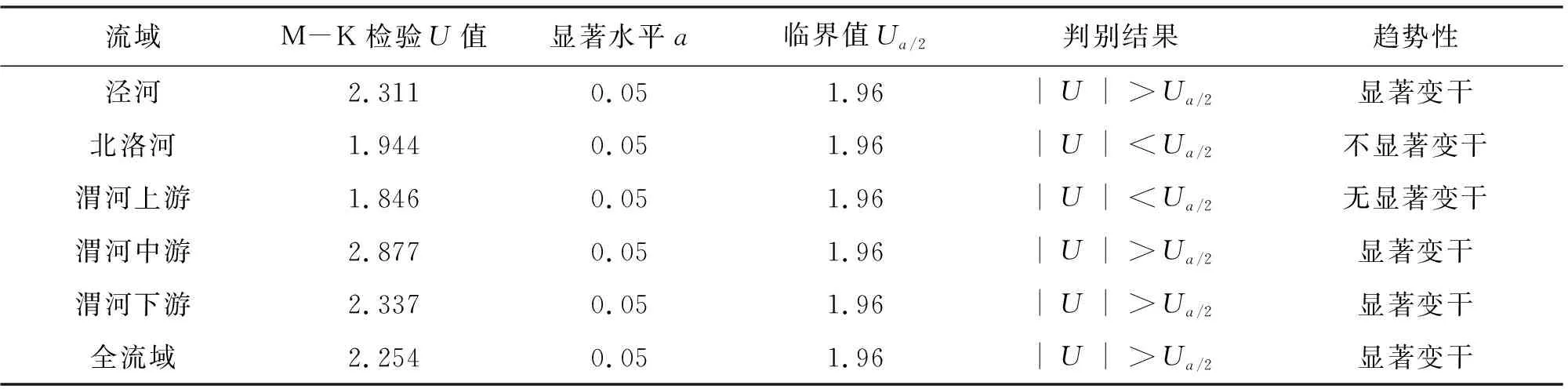
表5 1960-2010年研究区各子流域年际干旱变化趋势

由表5可知，在研究区5个子流域中，除渭河上游MHDI特征值U=1.846<1.96之外，其余4个子流域的特征值均大于或接近临界值 1.96(其中北洛河M-K检验U值为1.944，考虑到假设检验中，显著性水平为事先设定，因此当计算结果与临界值十分接近时，只要稍微放宽判定条件，也可认为有变干趋势[25])，流域在年际尺度上有明显变干趋势。其中渭河中游M-K检验U值达到2.877，变干趋势最为严重。

3.4 研究区年内干旱演化规律

(1)季尺度干旱变化。应用相同方法计算研究区年内综合干旱指数MHDI的M-K特征值U，本研究将年内尺度按春、夏、秋、冬4个季节划分，绘制流域各季节干旱趋势图，如图4所示。

从图4的中季节尺度来看，春、秋两季综合干旱指数M-K特征值U整体上均大于1.96，流域有明显变干趋势；夏、冬两季流域M-K特征值U均未超过临界值，表明流域未发生干旱，因此可以认为，年内尺度上，春、秋两季对干旱事件的发生起到主导作用。由图4还可以看出，春、秋两季干旱严重程度在空间尺度上有所不同，春季以渭河下游最旱，而秋季以渭河中游和泾河流域较为严重，这一认识可为流域季节性农业生产提供一定参考依据。

图4 研究区年内季尺度干旱趋势

(2)月尺度干旱变化。利用M-K法分别计算渭河全流域和各子流域年内月尺度MHDI的变化趋势特征值，结果如图5所示。

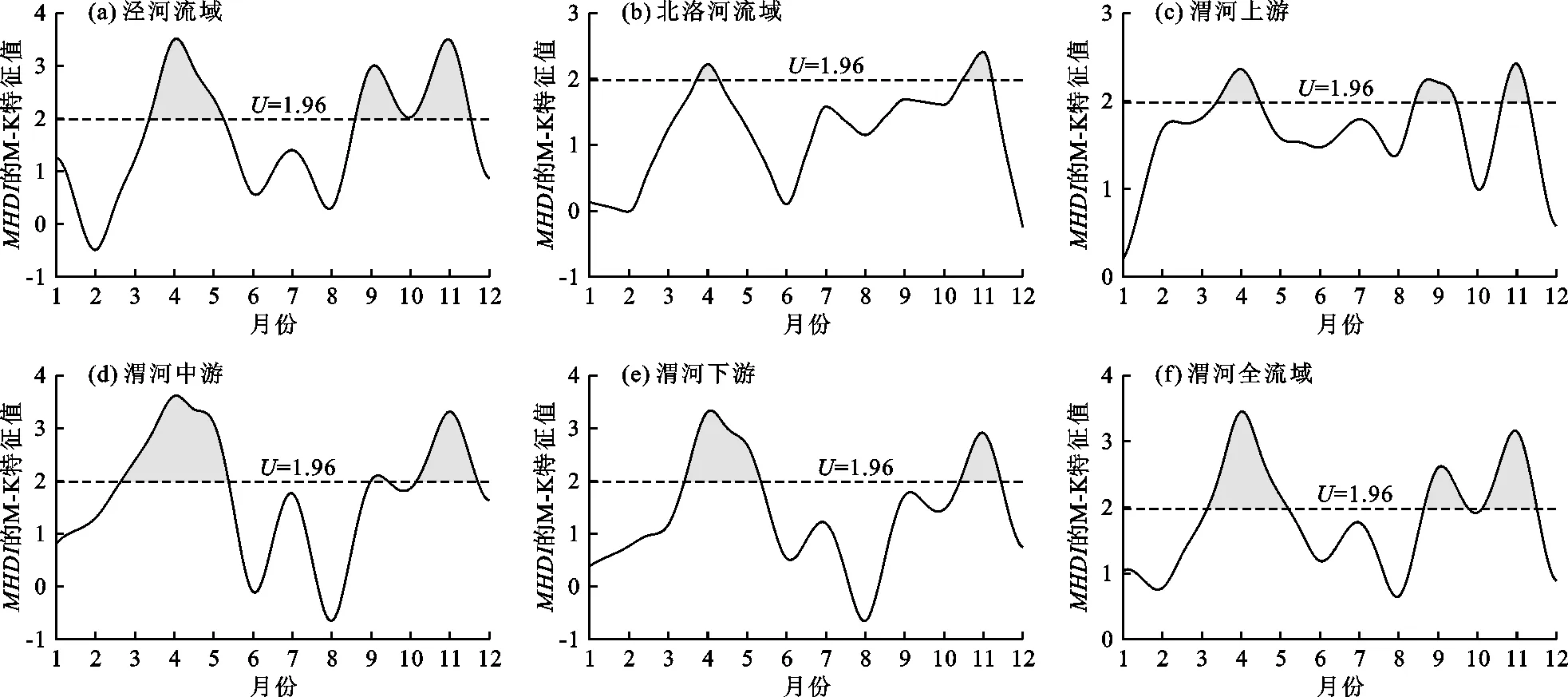
图5 研究区年内月尺度干旱趋势

图5表明，月尺度中，4和11月各子流域MHDI的M-K特征值达到顶峰，流域变干趋势最为显著，是流域干旱事件的主要来源，该结论与季尺度干旱事件来源相互吻合，因此可以认为，流域干旱频发的春、秋两季中，以4和11月对干旱事件贡献最大。在工农业生产中，上述两月应该重点关注。

3.5 研究区现阶段干旱风险评价

上述分析表明，渭河流域在年际和年内尺度上有变干的趋势，而在更长的年代际尺度上流域变干呈现波动上升趋势，MHDI值在20世纪90年代达到顶点后，自2000-2010年开始有所缓解，该缓解趋势在未来是否持续，是当地的农业生产、气象水文条件评估的重要依据，本研究采用R/S分析方案(rescaled range analysis)[26]，利用各子流域2000-2010年MHDI值计算对应的Hurst系数，判断下一个年代际(2010-2020年)流域的干旱状态。R/S分析方案是判断序列一致性的有效手段，具体原理和计算方法见参考文献[26]。各子流域Hurst系数值如图6所示。

由图6可以看出，研究区各子流域Hurst系数均小于0.5，这表明在2010-2020年，流域干旱趋势与过去临近一段时间保持一致，即干旱状态有所缓解。从空间尺度来看，渭河上游的Hurst系数最小，干旱最先从该子流域缓解，其余干旱缓解顺序为北洛河流域→渭河中游→渭河下游→泾河流域。黎云云[27]的研究成果表明，在更大的尺度上，黄河流域(包括渭河流域)未来30年内(2021-2050年)将不容易发生长历时(3个月以上)的气象干旱事件，该结论与本文预测结论相互印证。

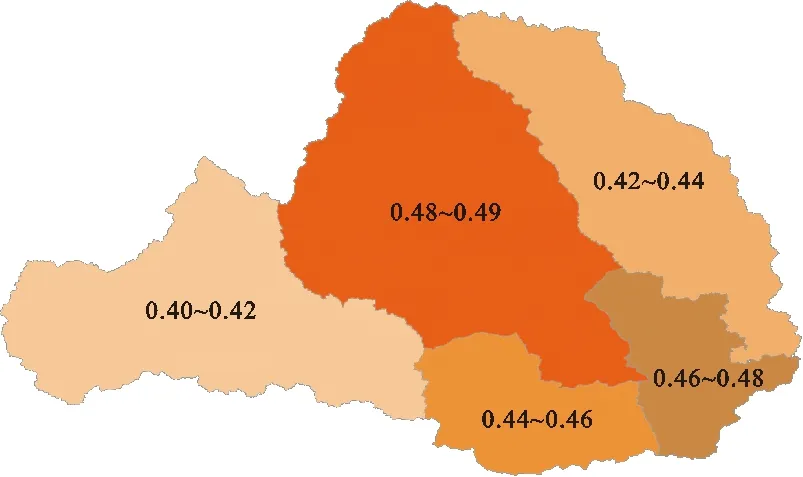
图6 2010-2020年研究区各子流域Hurst系数空间分布

将各子流域MHDI值的Hurst系数用克里金法插值到渭河全流域中，如图7所示。由图7可以明显看出，在未来一定时期，泾河流域、渭河中游、渭河下游三者交汇处(区域1)的Hurst指数最大，其次为渭河下游出口处(区域2)。这表明即便在未来干旱有所缓解的趋势下，上述两个区域仍需持续关注。通过进一步分析可知，区域1所覆盖范围包括西安及其周边地区，区域2覆盖范围包括临潼区和华县。西安是我国西部地区核心枢纽，也是西北五省主要的特大城市之一，截至2020年底，常驻人口超过1 000万人，因此较慢的旱情缓解对城市工业生产、人民生活、城市供水、供电分配均会造成一定影响。因此，这一现象应在未来一段时期加以重视。

图7 渭河全流域Hurst系数空间插值分布

4 讨 论

本文将数学方法与干旱风险分析研究相结合，对传统单变量干旱指数进行赋权构建了综合干旱指数MHDI，通过流域年尺度下典型干旱事件和月尺度下极端干旱事件的验证，综合干旱指数MHDI可用于流域时空干旱风险分析。但仍有以下两个问题需要进一步讨论。

(1)本文选择的4种单变量指数，是否为分析渭河流域干旱事件的最佳指数、是否在全流域范围内对不同干旱类型通用，限于篇幅并未对此做定量研究。但根据经验来看，并不乐观。因此如何根据不同流域、不同干旱类型选择合适的单变量干旱指数作为计算基础，仍是未来研究的关键所在。事实上，该问题一直以来也是传统干旱研究领域的一个热点问题。

(2)显然，由第1点讨论内容可知，由不同的单变量干旱指数应用本文方案构建的综合干旱指数在识别流域各时空尺度下干旱事件的能力方面也有所不同，因此下一阶段的研究，可向建立多目标综合干旱指数数据库的方向探索，以期更加丰富干旱研究的有力工具。这项工作属于“地球气候的物理建模”范畴，可用于量化气候系统及预测全球变暖(变干)趋势，这也是2021年诺贝尔物理学奖获得者Syukuro Manabe和Klaus Hasselmann目前仍在进行的主线工作[28]。

5 结 论

以降水距平百分率、标准化降水指数SPI、河道来水量距平百分率、修正Palmer干旱指数PDSI等4种常用指数构建综合干旱指数MHDI，典型干旱事件和极端干旱事件检验结果表明，MHDI指数在研究流域具有良好的适用性。本文主要结论如下：

(1)1960-2010年渭河流域年代际干旱呈现波动上升趋势，在20世纪90年代严重干旱、极端干旱频次达到最大，各子流域平均出现了40次，2000-2010年旱情有所缓解。

(2)渭河流域年际干旱有整体变干趋势，M-K检验结果表明，泾河流域、渭河下游和渭河中游对全流域变干起主要贡献，北洛河流域起不显著贡献，渭河上游对流域变干无影响。

(3)渭河流域季尺度干旱状态呈现春秋干旱、夏冬缓解的趋势，其中春季以渭河下游最旱，秋季以渭河中游、泾河流域最旱；月尺度上表现为4和11月旱情最为严重，该结论与季尺度旱情在时间关系上相互对应。

(4)2010-2020年渭河流域各子流域MHDI值的Hurst系数检验结果表明，全流域旱情将持续得到缓解，流域旱情缓解顺序为渭河上游、北洛河流域、渭河中游、渭河下游、泾河流域；但西安地区旱情缓解较慢，应予以持续关注。