基于ARMA-GMDH的水利工程变形预测模型

李莉贞， 曾志全， 黄 勇， 杨 杰， 宋锦焘

(1.西安理工大学 水利水电学院， 陕西 西安 710048； 2.西北旱区生态水利工程国家重点实验室，陕西 西安 710048； 3.中国电建集团华东勘测设计研究院有限公司， 浙江 杭州 311122)

1 研究背景

目前我国共修建水利工程10万余座，这些工程在防洪、灌溉以及发电等方面发挥着重要的作用，产生了巨大的社会经济效益与环境效益[1]。但随着工程运行时间的增加，其安全问题也愈发严重。水利工程安全监测是对其变形、渗流、应力应变等效应量进行全面的观测，是分析水利工程运行性态、评价水利工程结构安全的有效手段之一。

水利工程变形预测是水利工程安全监测领域一个重要的研究方向，通过构建水利工程变形与水位、温度等影响因素间的非线性关系，定量评价其安全性态。针对水利工程变形预测问题，相关学者已经利用时间序列法、灰色理论、人工神经网络、贝叶斯等方法进行了深入的研究，取得了丰富的成果。例如李明军等[2]针对传统粒子群算法搜索时间长的缺点，调整学习因子，提出了改进的ELM-IPSO模型；陈诗怡等[3]针对传统模型中预报因子的选择问题，采用Copula函数结合随机森林理论，提出了Copula-RF模型。Li等[4]提出了一种大坝变形监测模型，融合了主成分分析、模糊均值和高斯过程回归等方法。Chen等[5]针对拱坝的变形，提出了一种目标叠加法，侧重于监测数据的空间相关性。Chen等[6]对向量机进行了改进，引入了蚂蚁狮子算法对其进行优化，可以用来预测混凝土大坝的变形。Qu等[7]提出了基于粗糙集和长短时记忆的预测模型，可以对大坝的单测点和多测点进行预测，并提出了一种新的预测模型评价体系。谢全敏等[8]利用薄壳理论对隧道围岩进行了变形预测。郭延辉等[9]构建了GM(1,1)模型，对溢洪道边坡变形进行了预测。

目前提出的变形预测模型，大部分都是将变形信号作为一个整体，通过引入人工智能算法及相关组合模型对荷载集与荷载效应集的关系进行学习并预测，而未充分考虑水利工程变形信号的内部特征，且变形影响因素复杂，水位分量、温度分量以及时效分量中既有线性成分又有非线性成分。因此，将线性分析模型与非线性分析模型相结合，对变形的预测分析具有较好的研究意义。

数据分组处理方法(group method of data handling, GMDH)已经被广泛应用于经济、军事、人口等领域，显示出其研究非线性问题的有效性，但是此方法很少应用于水利工程数据分析领域。GMDH属于自组织的系统建模方法，能够利用不完全的归纳算法实现最优复杂度模型的自动选取。与一般的人工智能算法相比，GMDH建模所需要的训练样本较少，不需要提前设定模型。但是GMDH建模过程是一个基于样本划分的有原则性的操作过程。自回归移动平均模型算法(auto regressive moving average, ARMA)是时间序列模型的一种，善于处理分析线性信号。通过将收集的数据按时间先后顺序排成一组序列，基于一种回归预测方法，可以预测出将来任意时间的变化。所以，引入ARMA算法，可以对GMDH算法无法处理的线性信号进行分析。

本文提出一种基于ARMA和GMDH模型的水利工程变形组合预测方法，先用ARMA算法对变形数据进行分析，得到线性成分的预测结果，再依据GMDH算法对剩余的非线性残差序列进行分析，得到非线性成分的预测结果。将两组结果合并即为组合预测方法的预测结果。组合模型发挥了两者各自的优势，可以实现水利工程变形的高精度预测。

2 算法介绍

2.1 GMDH算法

GMDH算法是乌克兰人Ivaknenko A.G.提出的。GMDH以参考函数构成的初始模型为基础，模仿生物的遗传、变异、选择、进化的方式，输入的数据通过两两交叉重组的方式产生新的中间模型集合，依据一定的准则，选择最优的中间模型并保留，再令其两两结合，不断地重复上述方式，直至产生一个最佳模型[10-13]。

GMDH算法的优点在于它能够依据输入和输出的原始数据构建一个模型，不需要设定函数关系式。其网络结构是随机的，在训练的过程中不断进行自我优化，具有神经网络的结构，在结构上具有自组织的特点，因此模型的拟合精度高于其他模型。

GMDH算法的基本建模步骤如下：

(1)将建模数据的N个样本数据分为两部分，训练集A(NA个数据)和检测集B(NB个数据)，N=NA+NB。训练样本用来产生模型，检测样本用来对产生的模型进行检验。一般情况下，假设有N个样本数据，选取2/3的样本数据作为训练样本，剩下的1/3样本作为检测样本[14]。训练集A用于训练模型的生成，检测集B用于检验中间模型。

(2)各层的输入变量两两交叉重组产生下一层的中间模型。一般采用Kolmogorov-Gabor(K-G)多项式作为传递函数产生中间模型：

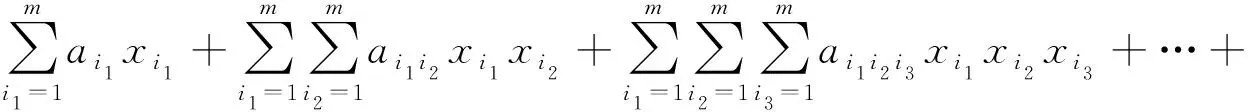
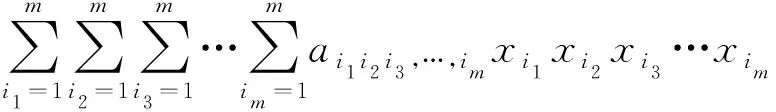
(1)

式中：xi(i=1,2,…,m)为输入变量；a为参数。

(5)每一层均重复步骤(2)～(4)，直到生成唯一的模型，停止GMDH网络的扩展构建，得到最终的GMDH网络。

GMDH算法的网络结构示意图如图1所示：

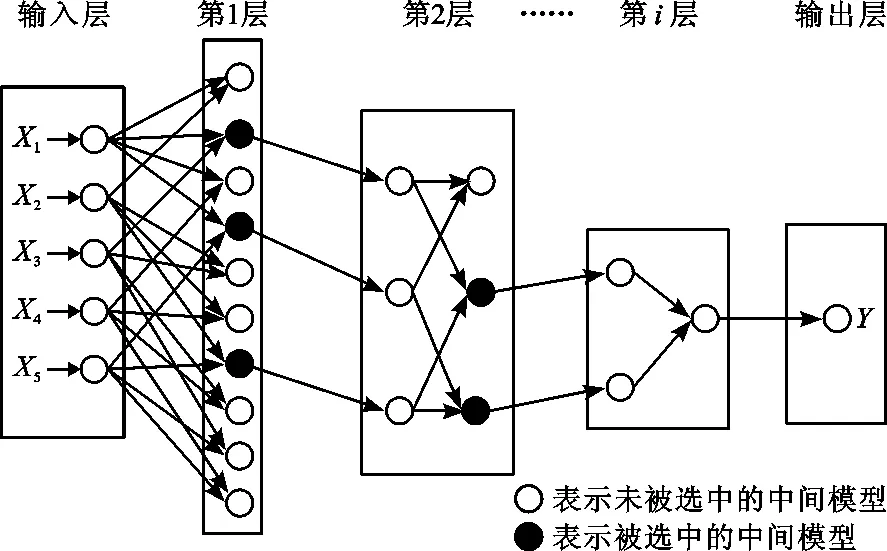
图1 GMDH算法的网络结构示意图

2.2 ARMA模型

时间序列是指数据按照时间的先后顺序而形成的一个动态数列。ARMA(p,q)模型是研究时间序列的一个重要方法，是由自回归模型(auto regressive，AR)与移动平均模型(moving average，MA)为基础组合而成的[15]。

ARMA模型的基本原理是：将一组数据看成是一个序列，用已知的数学模型刻画此序列。模型和序列匹配成功后，就可以根据已知的数据对其进行预测[16-17]。其数学公式为：

yt=φ1yt-1+φ2yt-2+…+φpyt-p+εt-θ1εt-1-

θ2εt-2-…-θqεt-q

(2)

式中：yt为一个平稳的时间序列;p为自回归模型的阶数；φi(i=1，2，…，p)为模型的待定系数;εt为误差;q为滑动平均模型的阶数;θj(j=1，2，…，q)为模型的待定系数[18]。

ARMA模型主要分为3种类型，分别是AR(p)模型、MA(q)模型以及ARMA(p，q)模型。需要根据时间序列的自相关系数和偏自相关系数选择模型类别。自相关系数计算的是时间序列之间在不同时期之间的相关性；一时间序列中假设点xi+1与前p个点是线性相关的，偏自相关系数计算的是点xi与点xi-p的相关性。AR(p)模型的特点为该序列的偏自相关系数在p阶后为0，称之为p阶截尾；MA(q)模型的特点为该序列的自相关系数在q阶后为0，称之为q阶截尾；ARMA(p，q)模型的特点是该序列的自相关系数q和偏自相关系数p均表现出拖尾性。ARMA模型的识别方法归纳于表1。

表1 ARMA模型识别方法

2.3 ARMA-GMDH组合预测模型

GMDH算法能够依据输入和输出的原始数据构建一个模型，只需要数据和准则，不需要人为设定函数关系式。但是GMDH算法擅长预测的是非线性信号，不能准确反映出预测数据中的线性成分情况。因此引入ARMA模型可以有效地预测出数据中的线性信号。将水利工程变形位移构成的时间序列看成是由线性信号和非线性信号两部分组成的。分别发挥ARMA模型和GMDH模型对线性模型和非线性模型处理的优势，将二者组合构建ARMA-GMDH预测模型，实现对水利工程变形的预测[19]。利用组合模型进行预测的操作步骤如下：

(1)采集一段时间水利工程原始的变形位移监测数据，构成历史位移时间序列。

(2)首先对已有的时间序列数据进行平稳性检验，若数据符合平稳性要求，则得出位移监测数据的自相关系数和偏自相关系数；若数据不符合平稳性要求，则对数据先进行取对数的操作，然后再进行平稳性检验[20]。

(3)根据数据的自相关系数和偏自相关系数得到ARMA模型。利用ARMA模型进行数据预测，得到线性部分预测结果序列L1；

(4)将上一步得到的预测结果序列L1与水利工程原始的变形位移监测数据相减，得到残差序列N；

(5)将非线性残差序列N作为GMDH模型的数据输入。将输入数据分为训练样本和测试样本，利用GMDH网络对输入数据进行训练，得到非线性部分预测结果L2；

(6)将线性部分预测结果L1和非线性部分预测结果L2组合，得到最终预测结果Y=L1+L2。

综上所述，ARMA-GMDH算法的流程如图2所示。

3 工程实例

实例分析选取水利工程中典型的水电站大坝作为研究对象。某水电站位于福建省周宁县境内，是福建省穆阳溪梯级的二级电站。该大坝变形监测包括坝顶水平位移、垂直位移等项目。大坝的测点(EX1～EX9)布置如图3所示，选取其中的EX1测点2016年6月2日至2017年7月6日的400个样本数据进行训练和预测。该测点的水平位移过程线以及相应的上游水位过程线如图4所示。

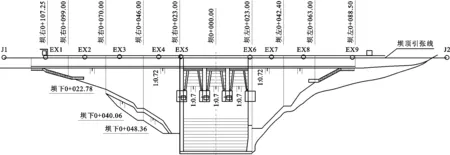
图3 实例工程大坝的测点布置图

首先对已有的400个数据进行平稳性检验，由图4可以看出，水平位移量是非平稳的。可以通过取对数的方式将位移量转化为线性趋势。ARMA模型需要确定p与q的值，可以利用自相关系数和偏自相关系数这两个统计量来确定ARMA(p,q)模型中的阶数[21]。

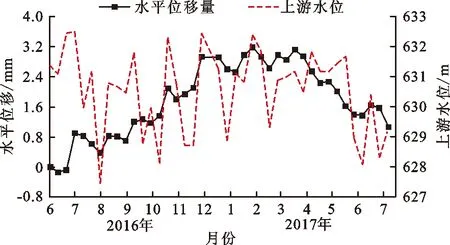
图4 EX1测点的水平位移过程线以及相应的上游水位过程线

图5为EX1测点水平位移量的自相关和偏自相关系数随滞后阶数衰减过程。由图5可以看出，自相关系数不是从某一阶突然跳变为0，而是逐渐衰减趋于0，表现出拖尾现象；偏自相关系数在1阶之后开始衰减，并迅速趋于0，所以该时间序列采取的模型为AR(1)。利用AR(1)模型对数据样本进行预测，得到的线性部分预测结果如图6所示。

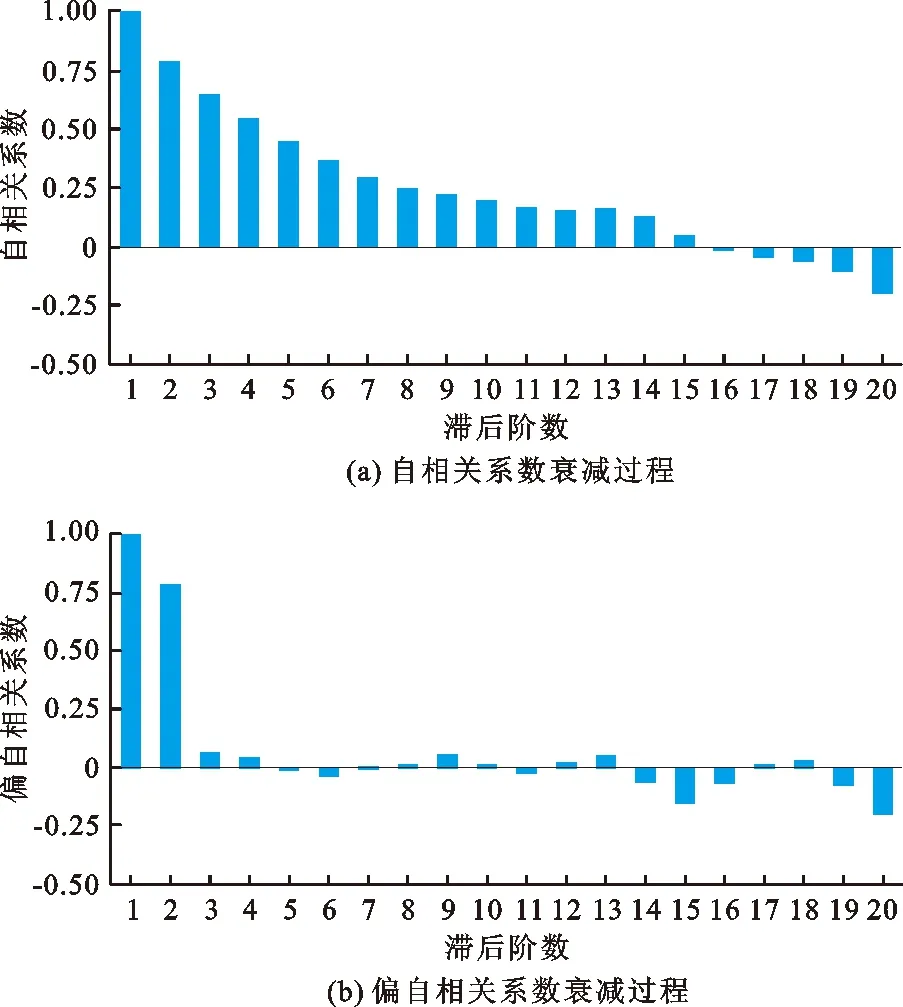
图5 EX1测点水平位移量的自相关和偏自相关系数随滞后阶数衰减过程

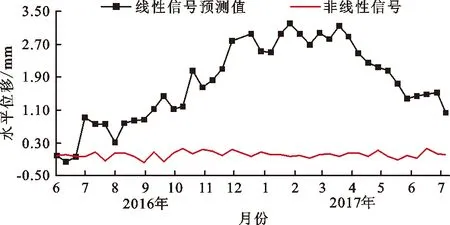
图6 AR(1)模型对数据样本线性部分预测结果

再将预测结果与大坝变形监测数据相减得到非线性残差序列，将其作为GMDH模型的输入数据，分为训练样本和检验样本，并选取了影响大坝水平位移的因素指标，如表2所示。

表2 大坝水平位移的影响因素指标

将前390个样本数据用于模型的训练，后10组数据作为模型的检验，得到非线性部分的预测结果。组合模型的预测结果即线性部分预测结果和非线性部分预测结果的整合，组合模型的预测误差如表3所示。

表3 ARMA-GMDH组合模型预测误差

为了对比分析ARMA-GMDH变形预测模型的预测精度，本文引入偏最小二乘回归PLSR(partial least squares regression)算法、BP(back propagtion)算法和GMDH算法分别建立预测模型，其中PLSR是经典的统计回归模型，BP算法是常用的人工智能算法，GMDH算法可以对比单一模型与组合模型的预测效果。采用的4种算法均由基于MATLAB2020的自带程序实现，图7为BP算法的相关参数及PLSR算法自变量系数直方图。

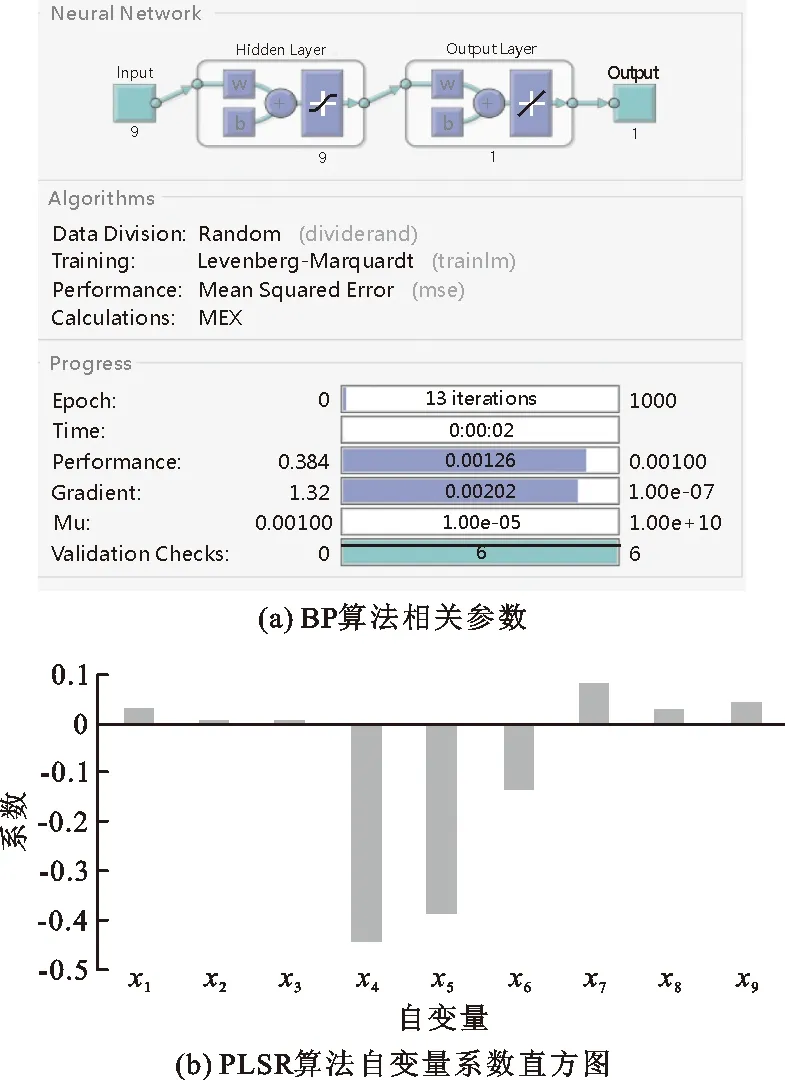
图7 BP算法的相关参数及PLSR算法自变量系数直方图

利用4种算法对相同的400个数据进行训练和预测，图8为4种算法的预测结果对比图，图9为4种算法的绝对误差对比图。

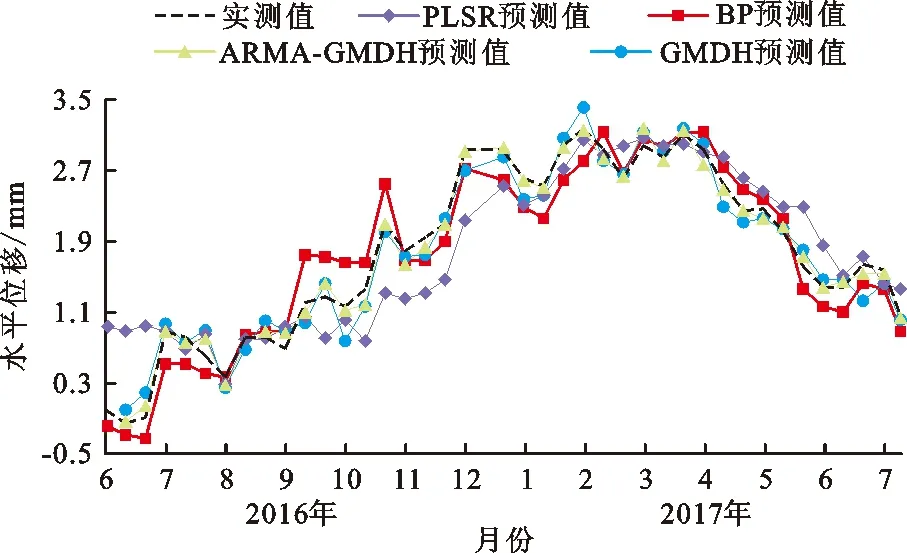
图8 4种不同算法的预测结果对比图

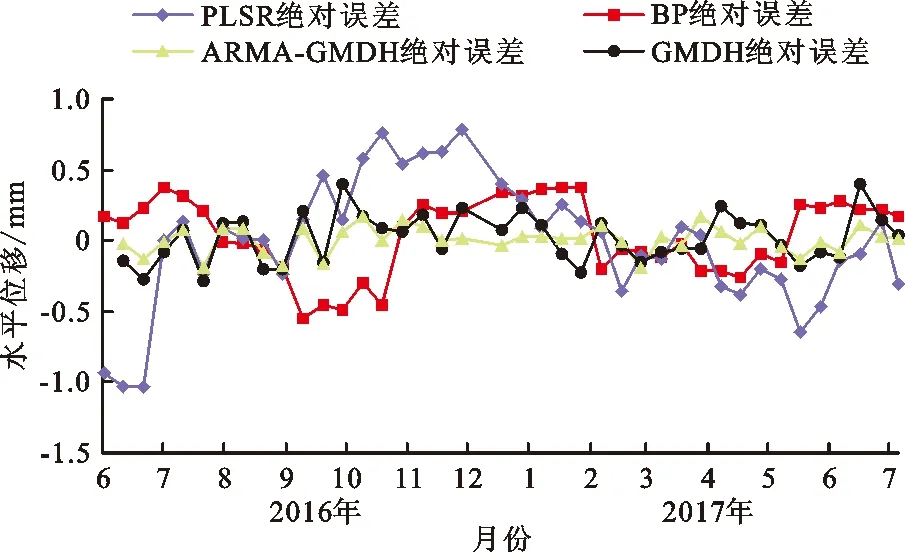
图9 4种不同算法的绝对误差对比图

为了验证ARMA-GMDH组合模型的预测性能，将其分别与基于PLSR模型、基于BP模型和基于GMDH模型的大坝位移预测模型进行对比，采用平均绝对误差(mean absolute error,MAE)、平均相对误差(mean relative error,MRE)、均方根误差(root mean square error,RMSE)和耗时4个评价指标来进行评价，4个模型的评价指标计算结果如表4所示。

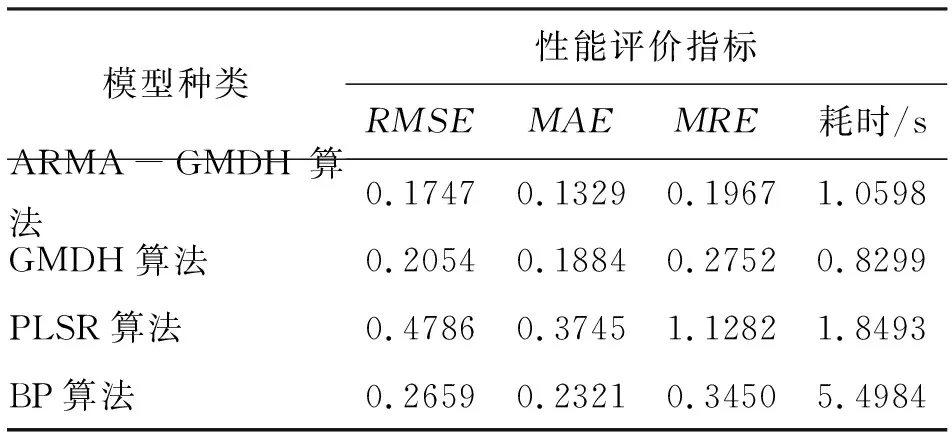
表4 4种算法预测指标结果对比

(3)

(4)

(5)

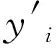
由表4可知：ARMA-GMDH算法预测结果的均方根误差和平均相对误差值分别为0.174 7和0.196 7；GMDH算法预测结果的均方根误差和平均相对误差值分别为0.205 4和0.275 2；PLSR算法预测结果的均方根误差和平均相对误差值分别为0.478 6和1.128 2；BP算法预测结果的均方根误差和平均相对误差值分别为0.265 9和0.345 0。4种算法中，BP算法耗时最久，为5.498 4 s；GMDH算法耗时最短，为0.829 9 s；ARMA-GMDH算法耗时为1.059 8 s，比单一的GMDH算法耗时略长。但由于ARMA-GMDH算法的均方根误差和平均相对误差都远远小于PLSR算法、BP算法和GMDH算法，且组合模型算法预测值的变化趋势都与实测值的趋势更为接近，可以忽略掉ARMA-GMDH组合模型的耗时略久。因此，所建立的基于ARMA-GMDH的大坝位移监测模型是切实可行的。

4 结 论

将擅长处理线性信号的ARMA模型和对非线性信号处理有优势的GMDH模型引入水利工程预测模型领域，建立了基于ARMA-GMDH的组合预测模型。结合工程实例进行了应用分析，得到了以下结论：

(1)与传统的PLSR算法和BP算法相比，GMDH算法的预测精度具有明显的优势。而ARMA-GMDH算法相较于GMDH算法，因为加入了善于处理线性信号的ARMA算法，弥补了GMDH算法的不足之处，具有较强的预测优势。

(2)提出的ARMA-GMDH水利工程变形预测模型能够较好地反映大坝位移的变化，对短期内大坝的位移预测具有一定优势，可以应用于大坝的监测系统，为大坝的位移预测提供参考。

(3)将善于处理线性与非线性信号的ARMA-GMDH预测模型引入水利工程领域，可以丰富水利工程的变形预测理论，对水利工程健康状态预测评估具有一定的工程指导意义。该预测模型不仅可以用于水利工程领域，还可以拓展运用于土木工程等其他领域的非线性信号预测，因此后续可以进一步开展基于ARMA-GMDH模型的土木工程结构变形预测研究。