电容式微机械超声换能器振膜设计与声学辐射研究*
高鹏飞, 何常德, 张彦军, 张文栋, 张国军
(中北大学 省部共建动态测试技术国家重点实验室,山西 太原 030051)
0 引 言
随着微机电系统(micro-electro-machanical system,MEMS)和集成电路(IC)工艺的快速发展,电容式微机械超声换能器(capacitive micromachined ultrasonic transducer,CMUT)因其宽频带[1~3]、可批量制造[4]、易于制造二维阵列[5~7]、易与IC集成[8]和高机电转换效率[9]等优势[1~9],已成为一种重要的新型超声换能器,在医学成像[10,11]、无损检测[12~14]、距离测量[15]等方面具有广泛的应用前景[10~15]。CMUT的设计对其性能指标至关重要,性能指标包括塌陷电压、谐振频率、灵敏度、声学辐射等[16~20]。
本文研究了CMUT设计的振膜材料、尺寸与声学辐射的关系。以经典薄板理论构成了CMUT建模的基础,分析了不同振膜设计的频率、振型,并根据瑞利—索末菲衍射公式计算相应的声学辐射。此研究比活塞辐射近似计算CMUT声场提高了准确性。此研究得到精确的CMUT声学辐射,对研究CMUT阵列的自辐射阻抗和相互辐射阻抗具有借鉴意义,可用于选择膜的几何形状和布局进行辐射阻抗的优化[21,22]。
1 CMUT建模与理论推导
1.1 CMUT振膜振动分析
CMUT结构包括上电极、下电极、振动薄膜、绝缘层、硅衬底以及真空腔,如图1所示。对上下电极施加电压可使>振膜振动发射超声波,下面首先运用薄板振动理论对振膜的振动进行研究,得到振膜的谐振频率与振型分布。

图1 CMUT换能器结构
由薄板振动理论可知,CMUT振膜属于边缘固支的圆形薄板结构。CMUT在真空或空气中的基频可用式(1)表示;基频即为一阶谐振频率,此频率对应的振动用式(2)表示
(1)
式中h为振膜厚度,a为振膜半径,E为杨氏模量,ρ为材料密度,σ为泊松比。由式(1)可知,CMUT的基频与振膜材料有关,且振膜厚度与频率呈正比,振膜半径的平方与频率呈反比
(2)
式中A为系数,基频的频率系数αa=3.196,r为圆上一点到圆心的距离,J0为零阶贝塞尔函数,I0为零阶虚宗量贝塞尔函数。由式(2)知,挠度w与r和时间t有关。
1.2 CMUT声学辐射
对于单个CMUT计算振膜向半空间辐射情况,根据瑞利—索末菲衍射公式(式(3))可以得到声场中任意一点的声压,圆形平板振动各参数如图2所示。式(3)如下
(3)

图2 振膜辐射所需参数示意
对于R≫a的区域声波到达观察点的振幅差别很小,振幅部分的h近似用R来代替,这里进行了远场近似,相位部分由图2得出式(4)
h2=r2+R2-2rRcos(r,)
(4)
式(4)取近似表示为
h≈R-rcos(r,)
(5)
将式(5)代入式(3)后,声压表示为
(6)
由式(2)得CMUT基频下的振速为

sin(2πft)
(7)
将式(7)振幅项代入式(6),并且利用贝塞尔函数的性质式(8)、式(9),解得CMUT辐射的声压如式(10)所示,指向性如式(11)所示
(8)
(9)
(10)
D(θ)=|D1+D2|
(11)
其中,D1,D2分别为式(12)、式(13)

3.196J0(kasinθ)J1(3.196)]
(12)

J1(kasinθ)+3.196J0(kasinθ)I1(3.196)]
(13)
式中 J1为一阶贝塞尔函数,I1为一阶虚宗量贝塞尔函数。从声压公式(10)看出,CMUT辐射声压与距离呈反比,与振膜半径的平方呈正比。不同的振膜材料、尺寸会产生不同的ka值与不同的声场分布,可视化结果可以由下文仿真看出。
2 仿真计算
2.1 CMUT振膜特性仿真
首先对不同振膜材料、尺寸的基频进行研究。CMUT振膜材料包括:硅(Si)、氮化硅(Si3N4)、磷化铟(InP)、氧化锌(ZnO)和多晶硅(Poly-Si),不同材料的参数见表1所示。

表1 不同材料的参数
以多晶硅材料制作CMUT薄膜为例,当CMUT薄膜半径a=30~100 μm,薄膜厚度h为1,2,3 μm时,根据式(1),可以获得CMUT薄膜的振动频率随薄膜半径和薄膜厚度的变化情况,如图3(a)所示,振膜越厚,频率越大。当以膜厚为2 μm,半径30~100 μm,计算不同材料的一阶频率(如图3(b)所示),可以看到,当半径增大时,谐振频率迅速减小,当减小到一定程度时,频率变化趋于平缓。

图3 不同振膜设计的基频
对于圆形振膜在基频下的振型分布可由式(2)得出,式(2)振幅项只与位置有关,振膜的振幅分布如图4所示,可以看到,一阶振型是沿中轴线对称的,振膜中心振动最大,边缘为零。
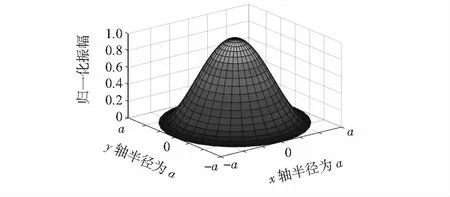
图4 CMUT一阶模态
2.2 声学辐射仿真
在对振膜基频与模态仿真基础上进行CMUT声学仿真。由式(10)、式(11)知,CMUT的辐射性能与ka值有关,以膜厚为3 μm,空气为传播介质,计算不同振膜材料半径的ka值,如图5所示。可以看到,多晶硅材料ka值最大,不同的振膜尺寸设计也会产生不同的ka值。

图5 不同材料和半径对应的ka值
根据式(10)计算基频下不同ka值CMUT的发射声场,并与活塞振动模型声场进行对比,频域的声场如图6所示。对比活塞与CMUT的发射声场,可以发现,随着ka的增大,两者指向性都增强,但活塞比CMUT指向性增强速度快,活塞辐射先出现旁瓣。所以,当ka较小时,两者辐射声场基本相同,可用活塞声场近似CMUT声场,ka较大时,两者的旁瓣角度不同,不能近似代替。

图6 不同ka值的CMUT与活塞辐射声场对比
根据式(11)计算基频下不同ka值CMUT的指向性,并与活塞振动模型指向性进行对比,如图7所示。对比活塞与CMUT振源的指向性发现,随着频率变大,两者主瓣都变窄;活塞型声源的旁瓣幅值比CMUT声源大;相同频率下,活塞型声源主瓣宽度比CMUT窄。
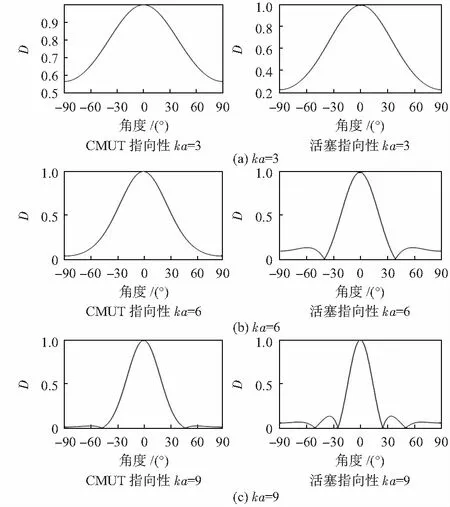
图7 不同ka值的CMUT与活塞辐射指向性对比
通过以上仿真计算直观展示了振膜材料、尺寸与ka的关系,从而将振膜的设计与CMUT的声学辐射建立了联系。
3 测试结果与分析
利用激光测振仪(Polytec,MSA—400)对CMUT的基频振动进行测试[23],对CMUT施加的交流电压为20 V,测试结果如图8所示。图8(a)测试结果表明,CMUT实际振动模态与仿真模态(图4)基本一致,在振膜边缘处位移为零,振膜中心位移最大。由图8(b)谐振峰可知,此CMUT的基频约为1.257 MHz。实验所用CMUT振膜材料为多晶硅,振膜半径为90 μm,膜厚为2.83 μm,由式(1)计算得到其基频为1.44 MHz,理论值没有考虑上电极与振膜的相互作用等因素,存在偏差也可理解。

图8 激光测振仪测试CMUT模态与基频
4 结束语
本文研究了CMUT在基频振动时振膜设计与ka值的关系,并得到了不同ka下CMUT的声学辐射。同等条件下与活塞辐射模型相比,由振动模态建立的CMUT辐射模型具有较弱的指向性与较低的旁瓣,比活塞模型近似计算CMUT声学辐射提高了准确性。此研究对CMUT阵列辐射阻抗的优化也具有参考意义。

