职前教师和在职教师KCS的比较研究
——基于问题提出的视角
朱亚丽
(河南师范大学 数学与信息科学学院,河南 新乡 453002)
0 引言
1986年,SHULMAN提出了学科教学知识(Pedagogical Content Knowledge,PCK)[1]。随后,BALL D L等研究者将其应用于数学教育领域,提出“面向教学的数学知识”(Mathematical Knowledge for Teaching,MKT),并将内容与学生知识(Knowledge of Content and Students, KCS)作为PCK的一个下位概念提出[2]。KCS是数学教师关于学生如何学习具体内容的知识,是内容知识与学生知识的有机结合[3]。教师在教学过程中不仅要了解学生的已有知识结构和接受能力,还要了解学生现有的数学思维水平。
问题提出是提问者基于特定的问题情境形成并表达问题的认知过程[4]。问题提出的背后是学生数学思维的反映;问题提出不仅可以评估学生的思维,还是一种有效的教学策略。教师获得的关于学生知道什么以及如何思考问题的信息越多,他们为学生创造的学习机会就越多[5]。通过问题提出可以很好地发展教师的KCS,学生提出问题的过程是学生基于已有的数学经验,通过对问题情境的理解建构良好数学问题的过程。
从问题提出的视角看,KCS是指教师和学生在面对同一问题情境时,教师能否准确地预测学生所提问题,对学生已有知识结构、接受能力和数学思维准确把握的能力。
1 理论框架
以学生的实际表现为基准,从教师对学生已有知识结构、接受能力、数学思维的了解程度等三方面探讨职前教师和在职教师在KCS方面的差异。表1展示了比较框架及各指标的比较方式。
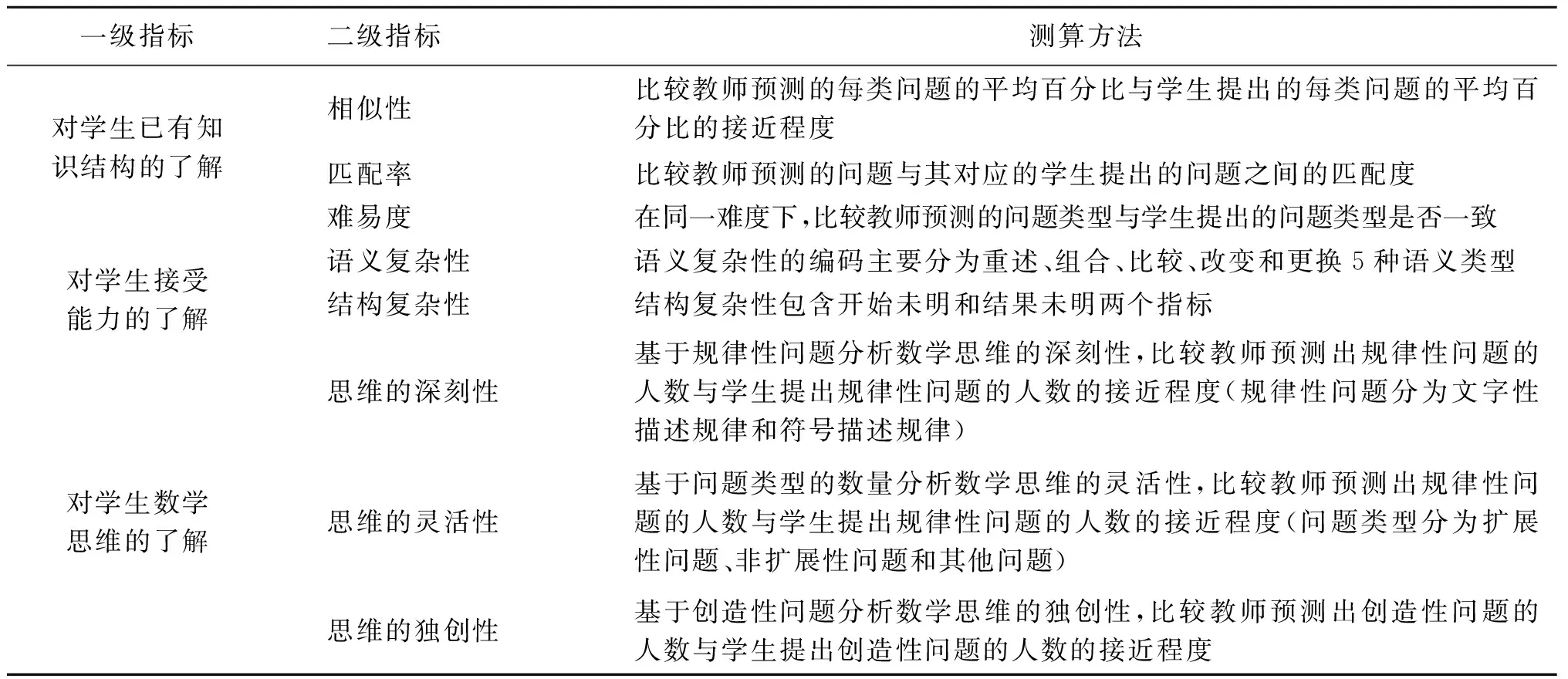
表1 职前教师和在职教师KCS比较框架及各指标的计算方式Tab.1 Comparison framework of KCS between pre-service and in-service teachers and calculation method of each indicator
首先,对学生已有知识结构的了解,是教师预测学生提出的问题和学生自己提出问题之间的相似性和匹配性。其次,对学生接受能力的了解,包括教师预测学生提出的问题类型与学生自己提出的问题类型难易度和复杂性的认知程度。数学问题的复杂性不是一个单一的概念,而是复杂的综合体[6]。因此又将复杂性分为语义复杂性和结构复杂性。语义复杂性的编码参考周若虹等人关于问题复杂程度的分类标准[7],分为重述、组合、比较、改变和更换5种语义类型。除其他问题之外,所有问题都可以根据语义复杂性或解决问题所需的关系数量进行分类,且问题的语义种类的范围在1到5之间。结构复杂性包含两个指标:开始未明和结果未明。开始未明是表述问题时,未知量并不在问题的结尾,如“在第几次铃声响起时有175个客人进入会场”。结尾未明是将未知量放在问题的结尾陈述,如“第(10)幅图形有多少个黑点”。再次,对学生数学思维的了解,从数学思维的深刻性、灵活性、独创性三方面综合评价职前教师和在职教师对学生数学思维的了解程度[8]。问题类型分为扩展性问题、非扩展性问题和其他问题,扩展性问题是指那些超越任务情境中所给定的初始图形或数量而提出的数学问题;非扩展性问题则局限于给定的任务情境,并没有跳出先前给定的图形或数量;无效问题指的是非数学问题、无解问题、表述不清的问题以及与题目毫不相干的无意义问题。独创性是指学生提出的某类问题在总问题中的占比不超过10%。
2 研究设计与方法
2.1 研究工具
测试卷分为三类:学生、职前教师、在职教师。测试题是由圆点情境和门铃情境等两个开放的问题情境组成的测试卷。两个情境均选自蔡金法等人有关数学问题提出的研究,具有良好的信效度。在测试卷中,要求学生根据给定的情境信息提出三个难度层次不同的数学问题:简单问题、中等难度问题、较难问题;在不知道学生提问结果的前提下,要求职前教师和在职教师根据自己对学生的了解,基于给定的任务情境预测学生在不同难度层次上会提出哪些数学问题。
2.2 研究被试
被试包含学生、职前教师和在职教师三个层次。学生被试和在职教师是河南省新乡市372名六至八年级学生及对应班级的数学教师,涉及该市三所公办学校;被试所在的学校不论是教育质量,还是教育资源都处于当地中等偏上水平。职前教师被试是河南省某师范院校的大三学生,其中52名是该校教育学院初等教育专业的师范生,122名是数学院数学与应用数学专业的师范生。三个层次最终收回的有效测试样本分布情况如表2所示。

表2 研究被试分布情况/人
2.3 数据编码
数据编码主要从问题类型和问题复杂性两方面分析被试提出的问题。先将被试所提的问题分为扩展性问题、非扩展性问题、其他问题;再根据问题的性质对每个扩展性或非扩展性问题进一步分类,见表3。基于上述编码体系,对所有被试提出的问题进行单独的编码分析,并将编码结果录入Excel软件。为了确保数据编码的可靠性,从各年级中随机抽取20%学生样本,30%职前教师样本,由两名评分者对他们所提的问题进行独立编码,由三名研究者对所有在职教师预测的问题进行独立编码。在学生和职前教师中,评分者之间的一致性均达到90%;对在职教师的编码一致性均在95%以上。
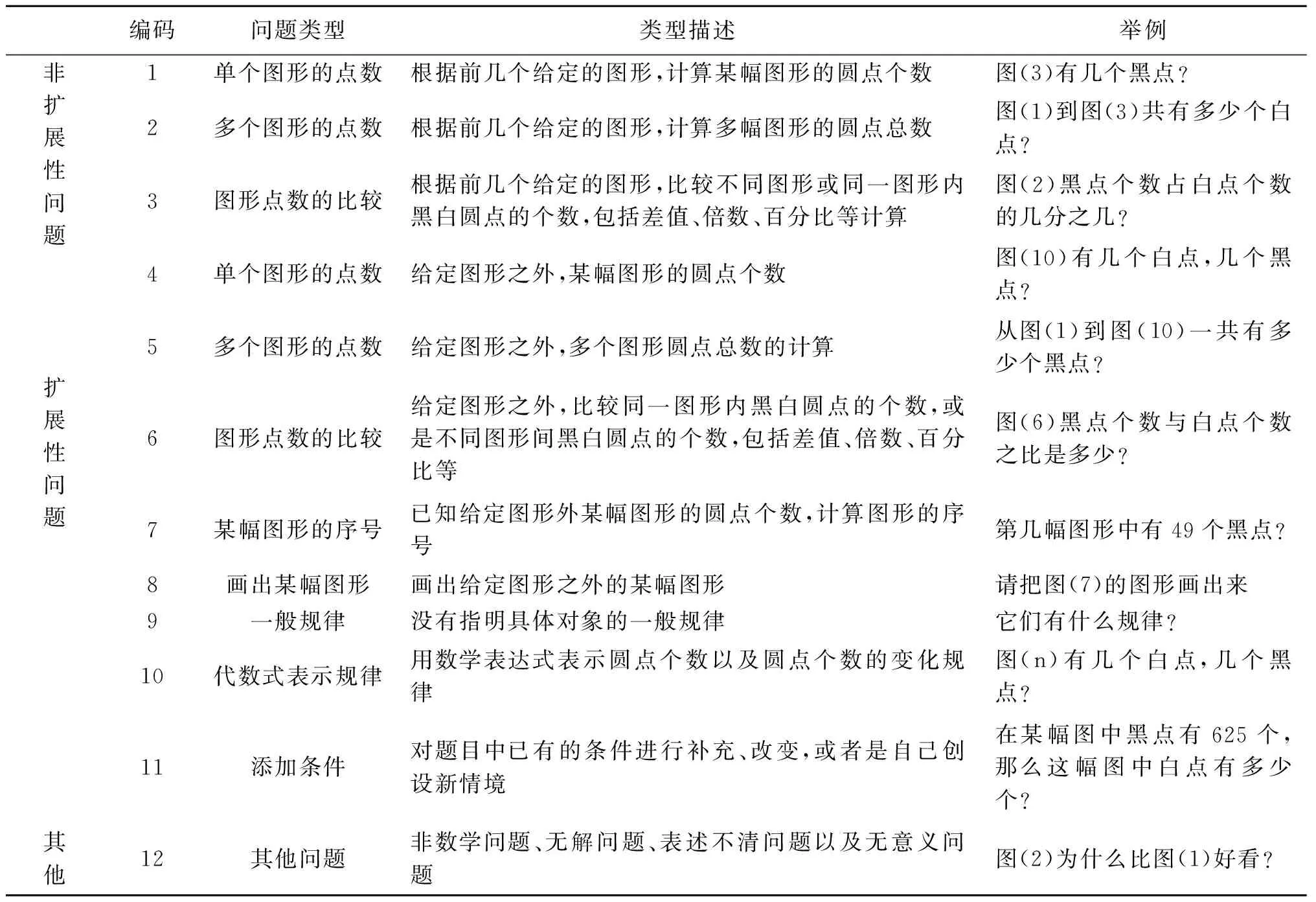
表3 圆点情境问题类型编码表Tab.3 Dot situation problem type coding table
3 研究结果分析
3.1 职前教师测试结果分析与讨论
1)在学生的已有知识结构上,职前教师认为具体的数值计算和代数式的应用占据主导地位。
无论是圆点情境还是门铃情境,职前教师预测最多的问题是单个图形的点数(类型4)、多个图形的点数(类型5)和代数式表示规律(类型10),见图1、图2。表明职前教师认为具体的数值计算和代数式的应用在学生的知识结构中占有很重要的地位,并且在三个年级中,职前教师预测的问题没有表现出明显的差异。此外,很少有职前教师预测反向提问(类型5~7)和创设新情境类(类型11添加条件)的问题,这说明职前教师认为学生在逆向思维和创造性思维上的表现相对较弱。
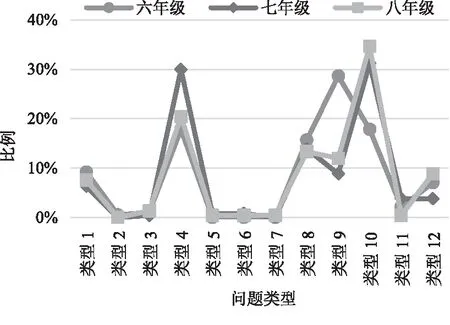
图1 圆点情境预测的问题类型分布Fig.1 Problem type distribution of dot

图2 门铃情境预测的问题类型分布Fig.2 Problem type distribution dot of doorbell
总之,虽然职前教师对学生的已有知识结构也有一定的了解,但在职教师对学生的了解更接近于学生的实际情况;在职前教师中,与六年级学生对应的职前教师对学生已有知识结构的掌握稍逊色一些,七年级、八年级之间没有显著差异;在三个年级中,在职教师对学生的已有知识结构的了解程度从高低的排序为:八年级>六年级>七年级。
2)在学生接受能力的了解方面,职前教师倾向于在简单问题中预测非扩展性问题和具体数值计算类问题,在较难问题中预测规律性问题和包含多种语义类型的问题。
首先,职前教师倾向于在简单问题中预测非扩展性问题和具体数值计算类问题,在较难问题中提出规律性问题。
从图3和图4可以发现,无论在哪种难度层次上非扩展性问题都不是职前教师的首要选择,且该类问题所占的比重随着问题难度的增加呈急剧下滑的趋势,尤其是在较难问题中没有职前教师预测非扩展性问题。总体而言,职前教师预测的问题绝大部分属于扩展性问题,非扩展性问题的占比随问题难度的递增呈现极速下滑的趋势。
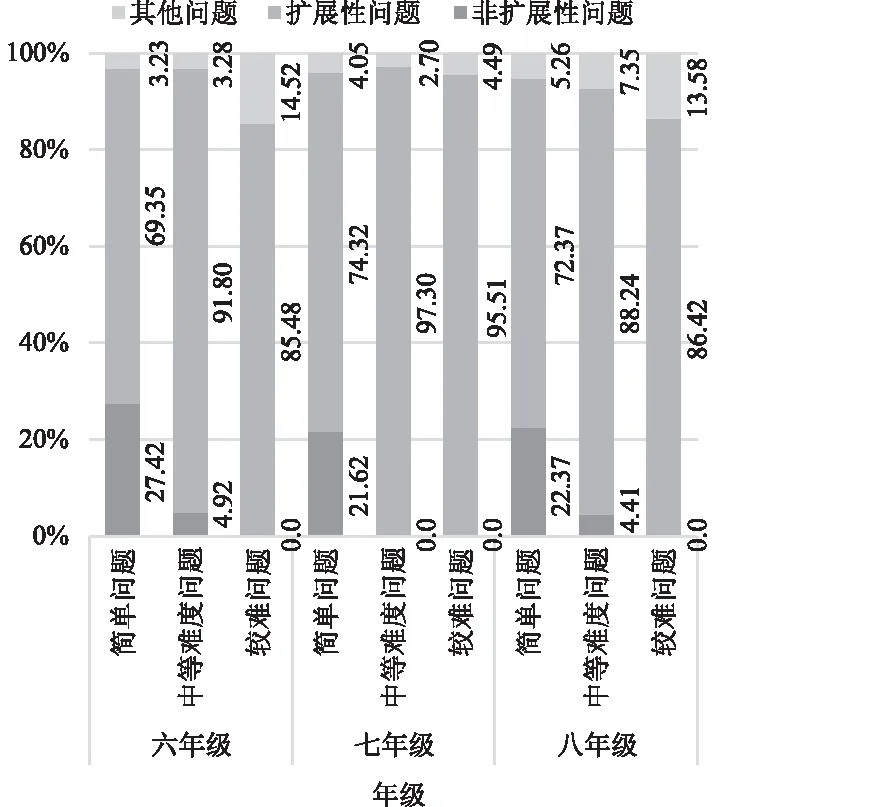
图3 圆点情境各问题类型的难易度分布Fig.3 Difficulty distribution of dot problem types
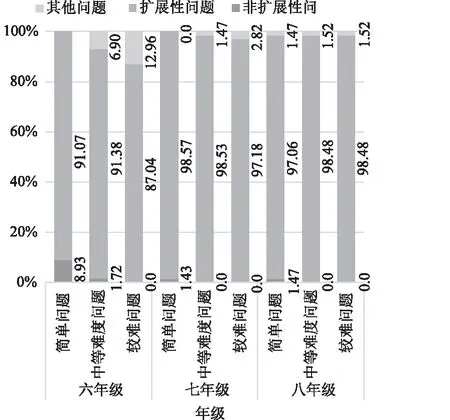
图4 门铃情境各问题类型的难易度分布Fig.4 Difficulty distribution of doorbell problem types
在圆点问题中,类型9在三个难易中占比较大,同时在门铃问题中,类型5较多,说明了职前教师偏向于将揭示情境的本质规律作为问题难度的评判标准。不管面对的学生处于哪个年级,职前教师都是在简单问题中预测具体的数值类问题,即计算某幅图形或某次铃响情况,在中等难度或较难问题中预测规律性问题。
其次,职前教师倾向于在较难问题中预测包含多种语义类型的问题。
表4和表5分别是职前教师在圆点情境、门铃情境中预测的包含多种语义的问题分别在不同难度层次的占比分布(P1、P2、P3分别表示简单问题、中等难度问题、较难问题)。观察表4、表5可知,不管是在哪种难度层次上,职前教师倾向于预测只含有一种语义类型的问题。尽管如此,涉及一种语义类型的问题的比重在逐渐降低,包含两种语义类型的问题的数量随难度的增加而增加。也就是说,职前教师认为学生会根据问题语义的多少判断问题的难易度。职前教师认为他们所预测年级的学生在结构复杂性上的表现并不理想,很少有职前教师预测“起始未明”型问题。事实上,职前教师在表述问题时通常是将未知量放在问题的结尾陈述,即使是基于逆向思维提出的问题,他们也会将未知量放在问题的最后。

表4 圆点情境包含多种语义的问题在不同难度层次的占比/%

表5 门铃情境包含多种语义的问题在不同难度层次的占比/%Tab.5 Proportion of doorbell situation questions with multiple semantics in different difficulty levels/%
3)职前教师认为,高年级学生思维深刻性的表现明显好于低年级学生,低年级学生在思维灵活性和思维独创性上的表现略优于高年级学生。
从表中数据综合分析,随着年级的升高,更多的学生能够提出规律性问题,这表明高年级学生具有良好的数学思维的深刻性。绝大部分职前教师预测了规律性问题,这表明职前教师认为他们所预测年级的学生数学思维的深刻性较好。
此外,绝大部分职前教师认为他们所预测年级的学生至少能从两种不同的角度出发提出不同类型的问题,一种是简单地模仿原有情境提问;另一种是通过提炼情境信息提问。低年级学生提出问题的类型多集中于三种类型,而高年级的学生则集中于两种类型,与其对应的职前教师的预测结果是一致的。
最后,不难看出,职前教师认为低年级学生思维的独创性相对较好,高年级学生思维的独创性有待提高。
3.2 在职教师测试结果分析与讨论
1)在学生的已有知识结构上,在职教师认为具体的数值计算和代数式的应用在学生的已有知识结构中占据绝对优势。
观察图5和图6可知,无论是圆点情境还是门铃情境,在职教师预测最多的问题无非以下两种:某幅图形或某次铃响情况以及给定模式的变化规律,表明在职教师认为具体的数值计算和代数式的应用在学生的知识结构中占有极其重要的地位,并且在三个年级中,在职教师预测的表现没有显著性差异。

图5 圆点情境预测的问题类型分布 Fig.5 Problem type distribution of dot
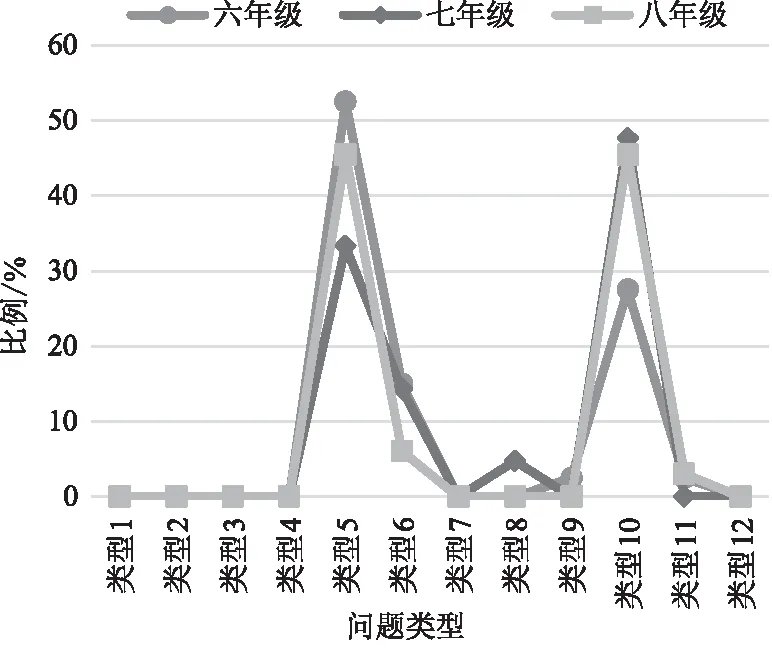
图6 门铃情境预测的问题类型分布Fig.6 Problem type distribution dot of doorbell
2)在学生接受能力的了解方面,在职教师倾向于在简单问题中预测具体数值计算类问题,在较难问题中预测规律性问题和包含多种语义类型的问题。
首先,在职教师倾向于在简单问题中预测具体数值计算类问题,在较难问题中提出规律性问题。观察图7和图8可知,无论在哪个难度层次上,在职教师预测的问题绝大部分属于扩展性问题。也就是说,在职教师认为他们所教年级的学生在提问的过程中不会过多地关注现有情境内部之间的关系。总体而言,在职教师认为他们所教年级的学生在提出问题的过程中,往往关注的是后续情境的发展趋势;他们通常是从给定情境出发思考问题,挖掘情境中的数学关系,进而提出扩展性问题。

图7 圆点情境各问题类型的难易度分布 Fig.7 Difficulty distribution of dot problem types
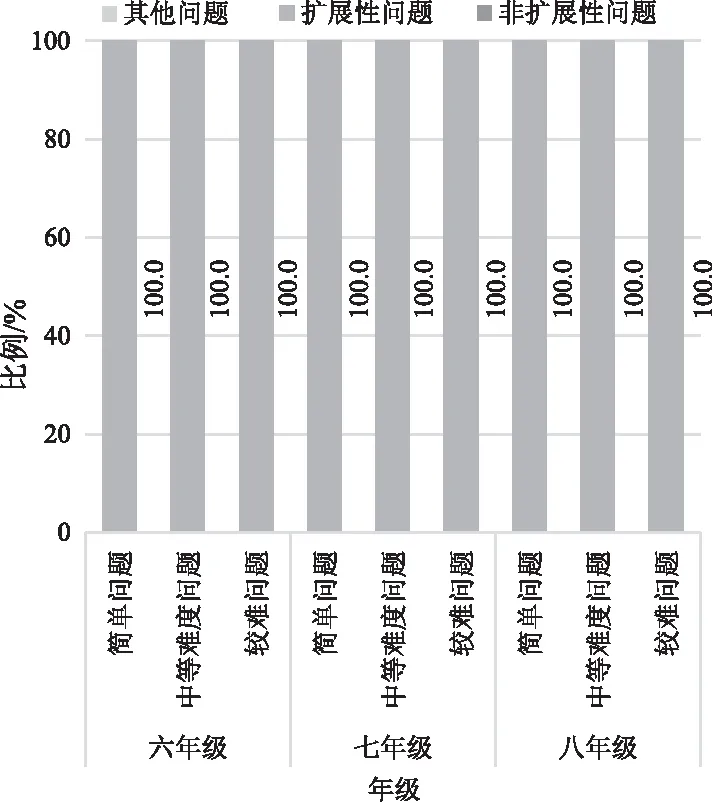
图8 门铃情境各问题类型的难易度分布Fig.8 Difficulty distribution of doorbel problem types
其次,在职教师倾向于在较难问题中预测包含多种语义类型的问题。表6和表7分别是在职教师在圆点情境、门铃情境中预测的包含多种语义的问题分别在不同难度层次的占比分布如图9、图10所示(P1、P2、P3分别表示简单问题、中等难度问题、较难问题)。
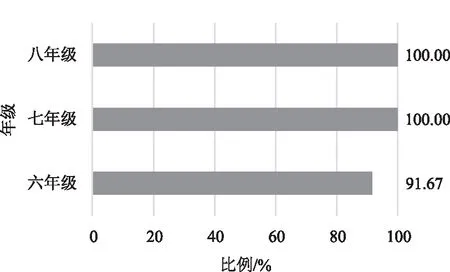
图9 圆点情境规律性问题的人数比较Fig.9 Comparison of the number of people with dot
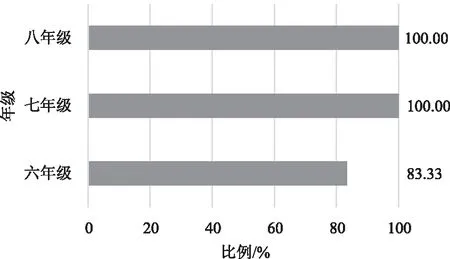
图10 门铃情境规律性问题的人数比较 Fig.10 Comparison of the number of people with doorbell

表6 圆点情境包含多种语义的问题在不同难度层次的占比/%

表7 门铃情境包含多种语义的问题在不同难度层次的占比/%Tab.7 Proportion of doorbell situation questions with multiple semantics in different difficulty levels/%
可知在简单问题中,各年级在职教师预测的问题均只包含一种语义类型,在中等难度问题上,在职教师会预测包含两种或三种语义类型的问题。在职教师认为他们所教年级的学生在结构复杂性上的表现不太理想。两种情境中在职教师均未预测“起始未明”型问题,所有的问题都是采用“结果未明”的结构进行表述的。
3)在思维的深刻性上,在职教师均预测所教年级的学生表现良好;在思维的灵活性和独创性上,在职教师认为低年级学生的表现较好,而高年级学生有待提高。
首先,在职教师预测他们所教年级的学生具备良好的思维深刻性。从在职教师预测的规律性问题的人数来看,高年级在职教师认为所教年级的学生思维的深刻性较好,善于揭示事物的本质规律,并用数学符号语言表示规律。低年级在职教师认为所教年级学生不会过多地关注事物发展的普遍规律,而是从现有的信息中挖掘其内在关系,思维的深刻程度相对较低。其次,低年级在职教师认为所教年级的学生思维较灵活,而高年级在职教师认为所教年级的学生思维灵活性有待提高。
从在职教师预测的问题类型的数量进行深入分析,六年级在职教师认为所教年级学生的数学思维的应变能力较强,学生能够摆脱已有模式的束缚,思维的灵活程度相对较高。七年级、八年级在职教师认为所教年级的学生会受思维定式的影响,直接将其视为规律类问题,且在提问的过程中,不会关注事物内部结构之间的关系,思维的灵活程度相对较低。
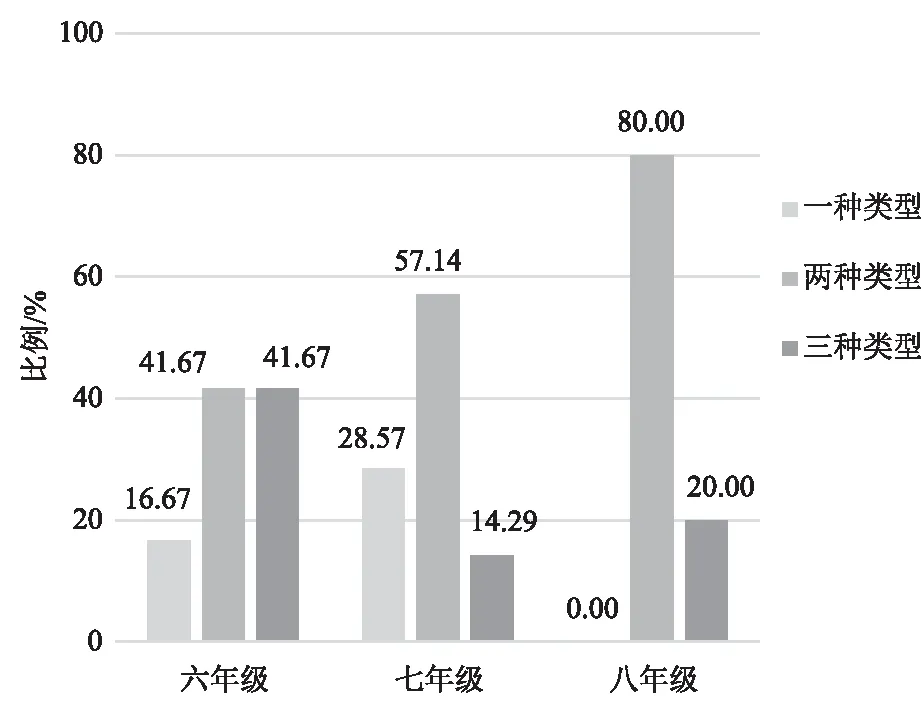
图11 圆点情境预测问题的类型比较Fig.11 Comparison of the types dots
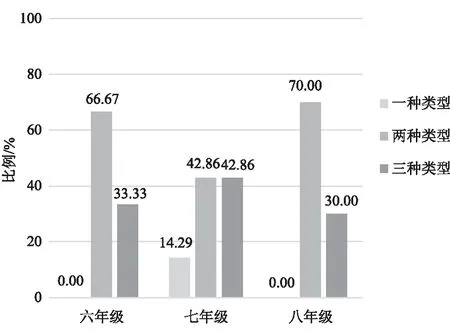
图12 门铃情境预测问题的类型比较 Fig.12 Comparison of the types of doorbell
最后,低年级在职教师认为他们所教年级的学生思维的独创性相对较好,高年级在职教师认为他们所教年级的学生思维的独创性相对较差。
可知,高年级在职教师认为所教年级的学生会受思维定式的影响,在创造性思维方面的表现不理想。而低年级在职教师认为所教年级的学生能摆脱思维定式,突破原有的思维方式产生新观点,提出一些新颖的、独特的问题,思维相对活跃,具备良好的创新意识。
4 结论与建议
4.1 在职教师对学生已有知识结构的了解程度明显优于职前教师
首先,从问题类型上看,在职教师的预测表现更接近于学生的实际水平。但是职前教师和在职教师均低估了学生的想象力和创新意识,高估了学生的抽象概括能力。其次,从匹配率上看在职教师预测的平均匹配率明显高于职前教师。这表明在职教师对学生知识结构的了解相对接近学生的实际情况,但还需进一步的发展。
针对以上问题,建议在职前教师的培养上,应将师范生的条件性知识和本体性知识相互融合。师范生的教育可借助PBL(problem-based learning)教学模式,引导师范生基于真实情境开展探索学习,并在完成项目中建构知识体系、深化理解[8]。高校与中小学合作构建“逐级递进、全程贯通”的实践教学体系。通过教师的指导,在实践岗位上基于真实的情境获得对课堂教学、跨学科教学的体验与反思,最终促进师范生获得对教师专业发展的完整知识体系[10]。
4.2 对于学生的接受能力,职前教师比在职教师有着更好的了解
首先,职前教师和在职教师均是过高地估计了学生对问题难易度的把握,但职前教师对问题难易度的预测更接近于学生对问题难易度的认识。其次,从问题的语义类型上职前教师的预测更接近于学生的实际水平。基于之前的分析得知,在两种情境中,学生提出的问题大都是“结果未明”型,很少提出“起始未明”型,而两类教师在预测问题中几乎都不涉及“起始未明”型。
在问题的复杂性上,职前教师对学生接受能力的了解更接近于学生的实际情况;职前教师和在职教师对学生接受能力的了解均无明显差异,三个年级的在职教师均低估了学生对多种语义类型的理解。
通过上述研究结论,对在职教师提出以下建议。首先,建立属于自己的“问题提出教学案例库”。教师在教学过程中将学生提出的问题做好整理与记录,进行有关教学内容与学生关系的分析,有助于教师了解学生的数学认知结构和数学思维,提升自身的KCS水平。其次,关注教育前沿领域研究、专业教学期刊等读物,有助于在职教师了解各阶段学生的认知水平,进而了解学生的接受能力,发展其KCS水平。
4.3 职前教师对学生数学思维的掌握情况略优于在职教师
1)职前教师和在职教师对学生数学思维深刻性了解情况均不理想,但职前教师的表现略胜一筹。职前教师和在职教师对学生数学思维深刻性的了解程度从高到低排序均为七年级>八年级>六年级。
2)职前教师更了解学生数学思维的灵活性。与六年级学生对应的职前教师对学生数学思维的灵活性的了解程度较弱,七年级、八年级之间没有明显的差异;八年级在职教师对学生数学思维的灵活性的了解程度较差,六年级、七年级之间的差异不显著。
3)职前教师对学生数学思维独创性的了解明显好于在职教师。与六年级学生对应的职前教师对学生数学思维的独创性的了解程度相对较好,七年级、八年级之间的差异并不明显;八年级在职教师对学生思维创造性的了解最差,而六年级、七年级之间没有显著性差异。
综上,建议尝试运用问题提出进行课堂教学。问题提出是理解学生数学思维的有力工具,运用问题提出进行课堂教学,有助于在职教师了解学生的数学思维,促进在职教师KCS的不断发展。同时建立“学生问题提出资源库”,及时记录课前未预测到的问题,逐步积累和增进自己对学生的认识。

