从空间到QK,ω,log(p,q)空间的积分型算子
2022-04-11 04:04尤晓琳
河南教育学院学报(自然科学版) 2022年1期
尤晓琳
(郑州工程技术学院 基础科学学院,河南 郑州 450044)
0 引言
设H(D)是复平面的开单位圆盘D上的所有解析函数全体,S(D)是D上的解析自映射全体。设φ∈S(D),对任意的f∈H(D),定义H(D)上的复合算子Cφ∶Cφf=f∘φ(参见文献[1-6])。
QK,ω,log(p,q)空间是满足
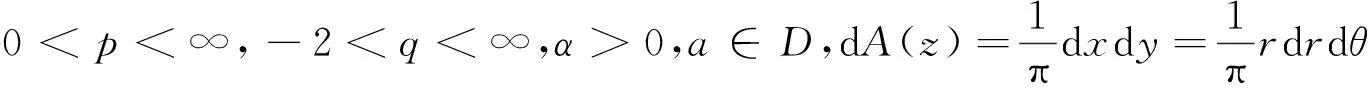
1 主要结论及其证明
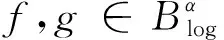

命题1的证明类似文献[1]中的命题3.11。

(1)
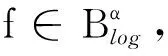


则
则(1) 式成立。

(2)
(3)

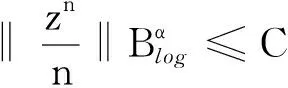
‖IφCφ(zn)‖QK,ω,log(p,q)→0,n→∞,
从而对每个r∈(0,1),对任意的ε> 0,存在n0∈N使得
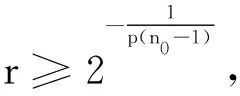
(4)
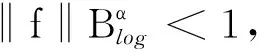
固定t,由(4)式得
(5)
(6)
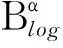
由(6)式, 对于δ=max1≤k≤Nδ(fk,ε) 和r∈ [δ, 1),
由引理1
则(3)式成立。
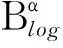
设r∈(0, 1),则
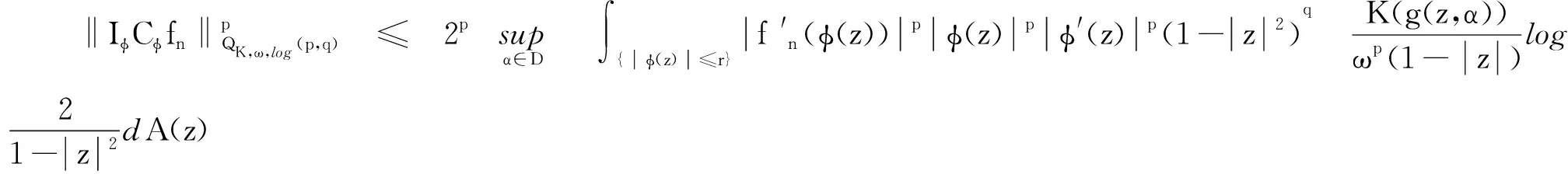
2pI1+2pI2。
由对每个ε>0,存在n0∈N使得对每个n>n0,
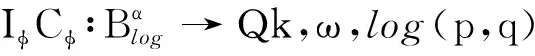
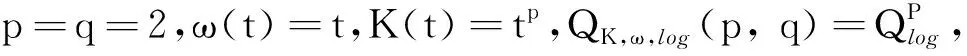
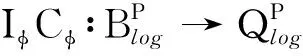
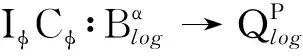
猜你喜欢
数学物理学报(2022年5期)2022-10-09
客家文博(2022年1期)2022-08-22
数学物理学报(2021年2期)2021-06-09
数学物理学报(2021年1期)2021-03-29
趣味(作文与阅读)(2021年11期)2021-03-09
趣味(语文)(2021年11期)2021-03-09
应用数学(2020年2期)2020-06-24
青年歌声(2018年2期)2018-10-20
对联(2011年24期)2011-11-20
对联(2011年18期)2011-11-19

