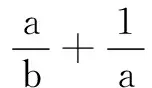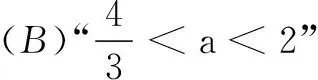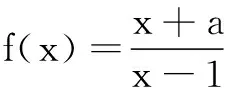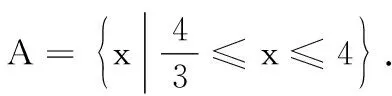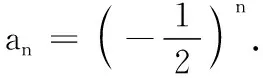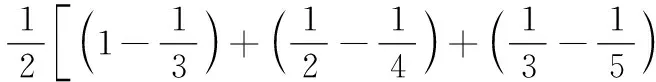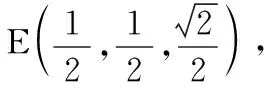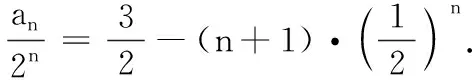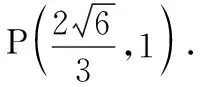高二数学测试
一、单项选择题(本大题共8小题,每小题5分,计40分)
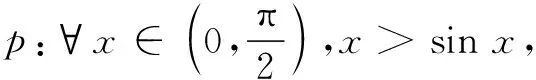
2.已知圆C1:x2+y2-kx+2y=0与圆C2:x2+y2+ky-2=0的公共弦所在直线恒过点P(a,b),且点P在直线mx-ny-2=0上,则mn的取值范围是( ).

3.设{an}是等比数列,若a1+a2+a3=1,a2+a3+a4=2,则a6+a7+a8=( )
(A)6 (B)16
(C)32 (D)64

(A) 圆上 (B) 双曲线上
(C) 抛物线上 (D) 椭圆上
5.对任意实数x,不等式(a-2)x2+2(a-2)x-4<0恒成立,则a的取值范围是( )
(A)-2 (B)-2≤a≤2 (C)a<-2或a≥2 (D)a≤-2或a≥2 6.《周髀算经》有这样一个问题:从冬至日起,依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种十二个节气日影长减等寸,冬至、立春、春分日影之和为三丈一尺五寸,前九个节气日影之和为八丈五尺五寸,问芒种日影长为( ) (A)一尺五寸 (B)二尺五寸 (C)三尺五寸 (D)四尺五寸 7.已知抛物线x2=4y的焦点为F,准线为l,P为抛物线上一点,过P作PA⊥l于点A,当∠AFO=30°(O为坐标原点)时,|PF|=( ) (C)2 (D)3 二、多项选择题(本题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分) 9.下列说法正确的是( ) (A)“a>1”是“a2>1”的充分不必要条件 (C)命题“∀x∈R,x2+1<0”的否定是“∃x∈R,使得x2+1≥0” (D)已知函数y=f(x)的定义域为R,则“f(0)=0”是“函数y=f(x)为奇函数”的必要不充分条件 来华留学生博士论文上出现的种种问题实际根源还在于我国高校留学生教育的不完善。与欧美等教育国家化程度较高的国家相比,我国留学生教育还存在不小的差距。国际化水平关键指标——来华留学生数量与高校外籍教师所占比例都远低于欧美日等发达国家。教育投入不足、教育资源有限、教学语言障碍、学位含金量不够都影响着我国留学生教育国际化水平。国际化水平决定着留学生博士论文管理水平,最终以留学生博士论文作为载体呈现。 10.如图,在正方体ABCD-A1B1C1D1中,以D为原点建立空间直角坐标系,E为BB1的中点,F为A1D1的中点,则下列向量中,不能作为平面AEF的法向量的是( ) (A)(1,-2,4) (B)(-4,1,-2) (C)(2,-2,1) (D)(1,2,-2) 11.已知数列{an}是等差数列,前n项和为Sn,且2a1+2a3=S5,下列结论中正确的是( ) (A)S7最小 (B)S13=0 (C)S4=S9(D)a7=0 (B)抛物线C2的准线方程是x=-2 三、填空题(本题共4小题,每小题5分,计20分) 13.若命题“∃x∈R,使得ax2+ax-3≥0”是假命题,则实数a的取值范围为______. (A)30° (B)120° (C)60° (D)90° 四、解答题(本题共6小题,计70分.解答应写出文字说明、证明过程或演算步骤) (1)求集合A; (2)若p:x∈A,q:x∈B,且p是q的充分不必要条件,求实数m的取值范围. (1)求实数a的值; (2)设g(x)=x+f(x),当x(x>1)为何值时,g(x)取得最小值,并求出其最小值. (1)求数列{an}的通项公式; 20.(本小题满分12分)如图,在四棱锥P—ABCD中,已知PC⊥底面ABCD,AB⊥AD,AB∥CD,AB=2,AD=CD=1,BC=PC,E是PB的中点. (1)求证:PB⊥平面EAC; (2)求二面角P—AC—E的大小. 21.(本小题满分12分)已知数列{an}的前n项和为Sn,a1=a,a2=2a+1,且Sn+1=3Sn-2Sn-1+n(n≥2,n∈N*). (1)若bn=an+n+1,问:数列{bn}为等比数列吗?如果数列{bn}为等比数列,请写出数列{bn}的通项公式;如果不是,请说明的理由. (1)求椭圆的标准方程; 参考答案 一、单项选择题 1.C;2.A;3.C;4.A;5.A; 6.B;7.B;8.B. 二、多项选择题 9.ACD;10.AC;11.BCD;12.BC. 三、填空题 13.(-12,0];14.90°; 四、解答题 (2)由x2-2mx+m2-1≥0,可得x≤m-1,或B={x|x≤m-1或x≥m+1}. 18.(1)由f(x)<0的解集为(-3,1),得f(x)=0的一个根为-3.所以-a=-3,得a=3. 所以当x=3时,g(x)取得最小值6. 20.(1)以C为原点,射线CD,CP为y轴和z轴的正方向,建立如图所示的空间直角坐标系,则C(0,0,0),A(1,1,0),B(1,-1,0). 又AC∩CE=C,AC,EC⊂平面ABCD,得PC⊥BC. 得二面角P-AC-E的大小是45°. 21.(1)由已知得Sn+1-Sn=2Sn-2Sn-1+n,即an+1=2an+n(n≥2).所以 由a1=a,a2=2a+1,得b1=a+2,b2=2a+4. 若a=-2,则b1=b2=0,{bn}不是等比数列. 22.(1)由x2=4y,可知焦点F(0,1).