向量法在平面几何问题中的应用

浙江省杭州第十四中学 (310006) 周 艳浙江省杭州第二中学钱江学校 (311215) 顾予恒

向量具有明确的几何背景，即有向线段，例如对平面几何图形中的边赋予方向，这些边就成了向量．几何对象与向量运算之间也有着对应的关系，例如线段长度对应于向量模长，垂直、平行关系对应于向量数量积与共线．本文探究利用向量来解决一些简单的平面几何问题．

用向量法解决平面几何问题主要依托于以下四样工具：

(2)向量数乘的意义和运算律，对应平行与共线的性质；

(3)向量数量积的意义和运算律，对应夹角，特别是数量积为零对应垂直；

向量法处理初中平面几何问题基本只需要这四条，体现了向量法简洁的特点．

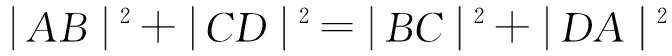
反之亦然，故互为充要条件．

点评：向量证明四步曲一气呵成，对称统一，给人以美的享受．本结论还可以推广到空间四边形中，向量法显现了问题的内在本质.

图1

例2(垂直问题)如图1，在正△ABC中，D,E分别是AB,BC上的一个三等分点，且AE,CD交于点P，求证：BP⊥CD．

点评：本解法是典型的向量法四步曲，选择基底并用它将几何图形中的对象表示出来，通过向量运算求解，并对向量结果进行几何翻译．

例3(平行问题)求证：梯形ABCD的两对角线的中点的连线平行于底边且等于两底差的一半．

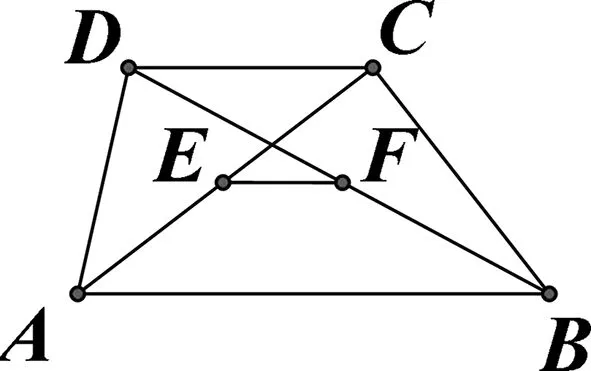
图2

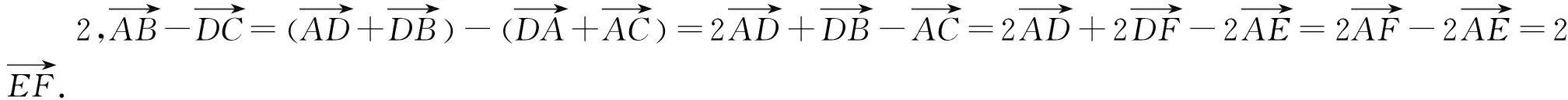
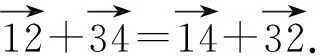
图3

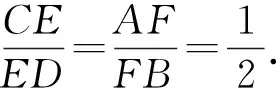
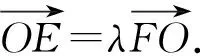
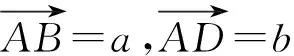
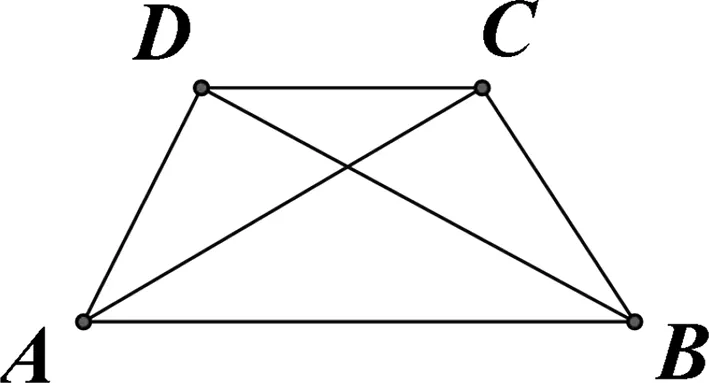
图4

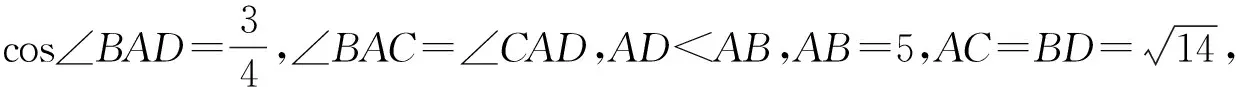
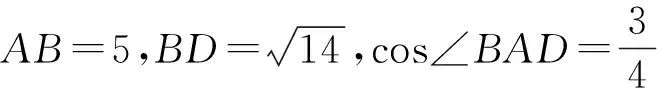
点评：平面图形与向量表示之间有着几何的内在联系，因此四步曲的第一步分析是必不可少的，借助平面几何知识与正余弦定理等工具分析清楚图形，有助于解决问题．

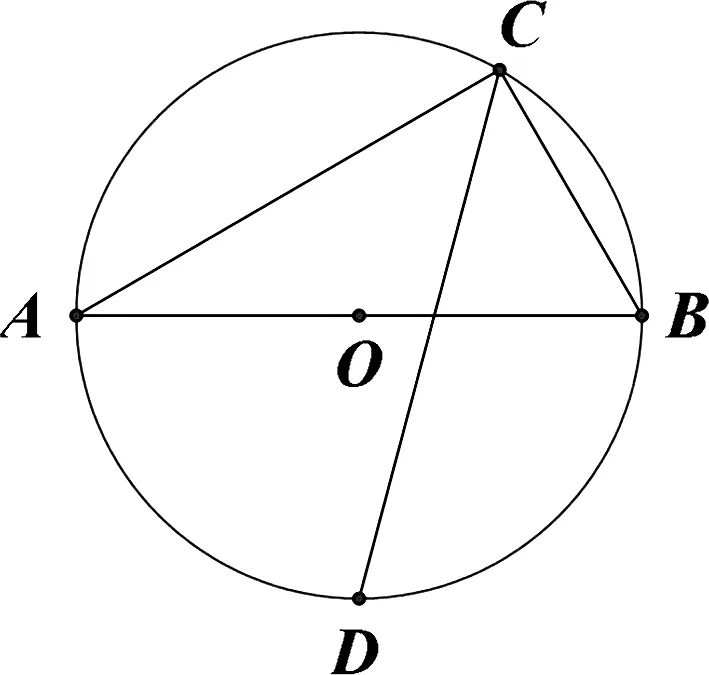
图5

例6(长度问题)如图5，AB为⊙O的直径，C为圆上(除A,B外)一点，∠ACB的角平分线交⊙O于点D，若AC=6，BC=2，求CD的长．

点评：本解法是典型的向量法四步曲，选择基底并用它将几何图形中的对象表示出来，通过向量运算求解，并对向量结果进行几何翻译，求线段长度往往与向量模长的平方有关．

图6

例7 如图6，扇形OAB的半径OA=3，∠AOB=90°，点C是弧AB上异于A,B的动点，过点C作CD⊥OA于点D，作CE⊥OB于点E，连结DE，点G,H在线段DE上，且DG=GH=HE，求证：CD2+3CH2是定值．

图7

例8(角度问题)如图7，直角△OAB中，∠AOB=90°,OA=3,OB=2，点M在OB上，且OM=1，点N在OA上，且ON=1，P为AM与BN的交点，求∠MPN．

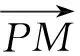
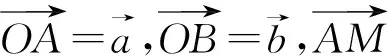
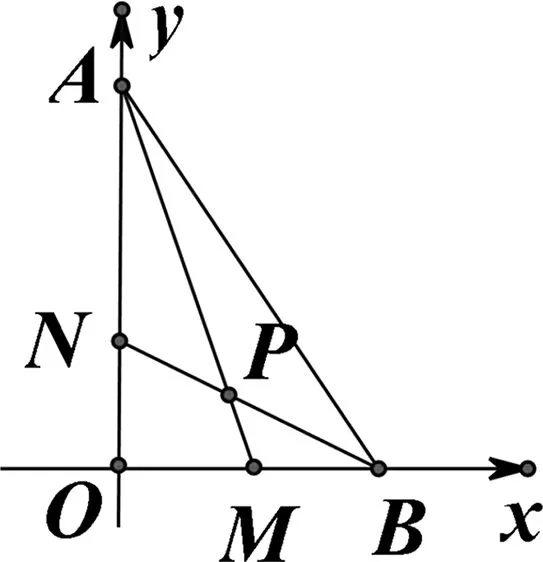
图8

点评：平面几何问题中求角度的问题，可以利用向量夹角公式来求解．建系坐标法也是向量法的一种形式．

图9

分析：要证的对象是长度之比，故考虑用向量共线来解决．

点评：不添辅助线，只是进行向量的表示转化，向量法处理平面几何问题可以变得如此简单．

图10

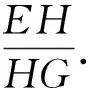
点评：利用平面向量基本定理里向量基底表示的唯一性，可以将一个向量分别表示为在两个共线向量上的分量的两种表示，从而求出分比．

例11(向量投影)圆O过△ABC的顶点A，且分别与AB,AC及BC边上得中线AD交于B1,C1,D1，求证：AB1·AB,AD1·AD,AC1·AC成等差数列．

图11

点评：本解法巧妙地利用了向量数量积中的投影视角，将两段共线的线段之积转化为数量积运算．

向量在整个高中代数与几何版块中起着统领作用，在其他知识模块中都有很多的应用，具有工具性的特征．经过本文的梳理，相信大家对用向量法解决平面几何问题有了更深的认识．平面几何问题，要学会遵循“先几何直观，再向量表示和运算”的顺序，对平面几何图形进行必要的几何分析，深刻领会向量法的关键在于选好“基底”，核心在于基于基本定理的表示，实质就是利用向量运算实现以数解形．