一道极值点偏移试题的求解与延伸*

福建省福清第一中学 (350300) 李云杰

极值点偏移问题以导数为背景考察学生运用函数方程思想、数形结合思想、转化化归思想解决函数问题的能力，层次性强，能力要求高，能够很好考查学生的综合素养，故此类问题一直是高考的热点.福建泉州市2022届高中毕业班第一次质量监测压轴题是一道极值点偏移问题，本文拟对该题作一些探究，与同仁交流.

(1)讨论f(x)的单调性；

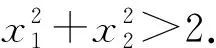
针对该题第(2)问，命题组给了两种参考解法.

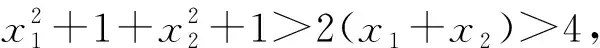
评注：解法一采用的构造函数法是求解极值点偏移类问题较为通用的方法，学生易于理解掌握.解法二通过引入参数t,m，将变量x1,x2统一用参数t,m表出，从而将待证不等式转化为参数t,m的不等式进行验证，此法也是处理极值点偏移问题比较有效的方法，只是此处引入两个参数，学生不易想到.

类似于解法二，笔者下面给出试题第(2)问的第三种解法.

试题延伸若(ex1)x2=(ex2)x1(e是自然对数的底数)，且x1,x2>0,x1≠x2，则

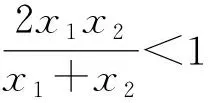
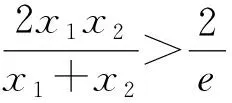
综上，结论成立.