基于联合卷积分析与合成稀疏表示的遥感图像分量替换融合方法

王文卿 尚 卓 周智强 刘 涵

（1.西安理工大学自动化与信息工程学院，陕西西安 710048；2.陕西省复杂系统控制与智能信息处理重点实验室，陕西西安 710048）

1 引言

近十年来，光学遥感卫星发展迅猛，捕获的遥感影像数据呈几何增长，在环境监测、变化检测和遥感图像解译等领域得到广泛应用。光学卫星提供的遥感影像通常包含两种类型：具有多个谱段的多光谱（MultiSpectral，MS）图像和仅具有单个波段的全色（PANchromatic，PAN）图像。多光谱图像含有丰富的光谱信息，但空间分辨率低，细节信息模糊。与之相反，全色图像具有较高空间分辨率，但光谱信息不足。然而，仅一类遥感数据很难满足用户对高空间分辨率和高光谱分辨率遥感图像的需求。因此，结合两者互补特性以获得具有高空间分辨率的多光谱（High spatial resolution MultiSpectral，HMS）图像成为遥感领域的一个热点问题。经过数十年发展，遥感图像融合技术已非常成熟。基于不同的理论模型，遥感图像融合算法主要分为以下四类［1-2］：分量替换（Component Substitution，CS）方法、多分辨率分析（Multi-Resolution Analysis，MRA）方法、基于模型的方法和基于深度学习的方法。

基于分量替换模型的常用算法有强度-色调-饱和度（Intensity-Hue-Saturation，IHS）变换方法、主成分分析法（Principal Component Analysis，PCA）、Gram-Schmid（tGS）变换方法等［3］。传统CS 方法的融合策略如下：首先将上采样至PAN 图像相同尺寸的MS 图像映射到一个新的特征空间，然后用直方图匹配后的PAN 图像替换上采样MS图像中代表空间信息的强度分量，最后通过逆变换得到HMS 图像。该方法简单、快速、高效，但容易产生光谱失真。在CS算法中，基于IHS变换的方法是最早提出的经典算法。传统IHS方法仅考虑了MS图像中红、绿、蓝三个波段与PAN 图像的融合，产生的融合图像光谱失真严重。为了解决这个问题，文献［4］提出了适用于四波段多光谱图像与全色图像融合的广义IHS（Generalized IHS，GIHS）方法，其中MS 图像的每个谱段具有相同的权重。为了适用于不同类型的遥感数据，文献［5］提出了自适应谱权重的IHS融合算法，利用多元回归方法计算自适应权重。针对分量替换方法容易产生光谱失真的问题，研究者提出从空间细节信息提取和空间细节信息注入两方面进行改进。自适应权重估计方法旨在获取最优的空间细节信息。然而，仅仅通过改善提取细节的方法并不能完全消除MS图像与PAN 图像的不适应区域。为解决该问题，文献［6］提出了基于统计比率的高频细节注入模型，通过部分替代的方式实现细节的有效注入，提高了融合图像质量。文献［7］中结合传统IHS变换与非下采样轮廓波变换，利用Gamma 校正和相关性分析，实现细节的有效注入，最终获得高质量融合图像。

基于多分辨率分析的典型算法有非抽样小波变换（UnDecimated Wavelet Transform，UDWT）［8］、“à trous”小波变换（“à trous”Wavelet Transform，ATWT）［9］、抽样小波变换（Decimated Wavelet Transform，DWT）［10］、拉普拉斯金字塔（Laplacian Pyramid，LP）［11］等。这类方法通过提取PAN图像的高频信息并将其注入到上采样MS 图像中以构建HMS 图像。多分辨率分析方法获得的融合图像相比于CS 方法具有更好的光谱信息，但容易产生空间失真。

基于模型的方法是通过构建描述低分辨率MS（Low resolution MS，LMS）图像、PAN 图像与HMS 图像间关系模型的目标函数，然后利用优化方法获得HMS 图像。然而，仅依赖谱保真模型和空间增强模型所得获得的HMS 图像质量并不高。为了提升融合图像的质量，研究者提出了许多先验模型来约束HMS 图像质量，如拉普拉斯先验［12］、非局部先验［13］和低秩先验［14］等。近年来，稀疏表示理论被广泛应用到遥感图像融合，成为基于模型方法的代表性算法之一。文献［15］首次提出了基于稀疏表示和压缩感知的遥感图像融合方法。在此基础上，结合不同稀疏模型，相继提出了基于字典学习的遥感图像融合方法［16-18］。基于模型的方法能有效提高融合图像的空谱保真度，但该类方法计算量大，复杂度高。

随着深度学习技术的迅猛发展，卷积神经网络（Convoluational Neural Network，CNN）被应用到遥感图像融合。受到基于CNN 的图像超分辨率方法［19］的启发，文献［20］提出了一种基于CNN 的全锐化（Pansharpening with CNN，PNN）方法，该方法采用了简单有效的三层网络结构。文献［21］提出了称为PanNet的深度网络结构，其通过充分考虑如何更好地保存空间信息和光谱信息来设计网络结构。文献［22］在PNN 方法基础上，采用了L1 损失函数、残差网络和更深的网络结构，提出了目标自适应全色锐化网络。文献［23］提出了一种双流融合网络，其设计了特征提取网络、融合网络和重构网络。基于CNN 方法的融合图像具有很好的空谱质量，但此类方法需要大量训练样本、模型对不同遥感数据的泛化能力差。

针对分量替换方法的光谱失真问题，本文提出了一种基于联合卷积分析与合成（Joint Convolutional Analysis and Synthetic，JCAS）［24］稀疏表示的改进融合算法。首先通过JCAS 算法对强度分量和均衡化PAN 图像进行分解，接着对分解后的基础层和细节层分别进行平均和取大处理。将融合后的基础层和细节层进行求和并与强度分量进行相减以获得第一幅空间细节图。第二幅空间细节图为直方图匹配后的PAN 图像与强度分量的差。为更好地利用这两部分细节信息，将强度分量与PAN 图像的相关系数作为权重对两部分细节信息的注入进行调整，以获得具有更高质量的融合图像。相比传统的分量替换算法，本文算法能够有效减小融合图像的光谱失真，同时具有较为清晰的空间结构。在定量指标评价上本文算法也优于对比算法。

2 相关工作

2.1 分量替换算法通用模型

分量替换法的通用模型如下：

其中k为MS 图像的波段数是上采样至与PAN图像相同尺寸的MS 图像，P为PAN 图像与强度分量I经过直方图匹配之后的图像，gk为细节注入系数，决定注入细节信息的多少为融合图像。

2.2 JCAS分解

Gu 等人在文献［24］中提出了JCAS 算法，旨在实现单一图像层分离。该算法利用了分析稀疏表示（Analysis Sparse Representation，ASR）与合成稀疏表示（Synthesis Sparse Representation，SSR）的互补机制。此外，该算法采用了卷积实现，可以有效的利用图像的全局信息。通过JCAS 算法可将单幅图像分解为具有大尺度结构的基础层和具有精细尺度纹理的细节层。一般情况下，给定一个输入图像，图像分离方法将其分解成两个分量U和V，即：

其中V和U分别表示细节层和基础层。

分析稀疏表示采用卷积方式来描述图像的稀疏先验。给定噪声图像Y，可以通过求解式（3）恢复清晰图像X：

其中||*||F表示F 范数，⊗表示卷积运算，Ri(fA，i⊗X)是惩罚函数，通过对分析系数正则化来增强潜在图像的先验知识。

合成稀疏表示的基本思想是通过尽可能少的非零系数来描述信号的主要信息，进而简化信号处理过程，其基本模型如下：

其中：y和x分别表示从输入图像和目标图像中提取的矢量化图像块；R(αs)表示合成系数的正则化项，用来表征合成系数的稀疏性。D为稀疏字典。此外，除了基于图像块实现的SSR 模型外，文献［25］提出了卷积稀疏编码方法。

ASR 和SSR 模型均利用了图像的稀疏先验，但它们具有不同的表示机制，因此在不同领域具有不同优势。JCAS算法结合了ASR和SSR模型的优点，可通过求解以下目标函数实现图像分离：

其中||*||1表示ℓ1范数；λ和γ表示正则化参数；{fA，i}i=1，…，M表示分析字典。SSR 分量被表示为V=表示合成字典，Zj是对应系数图。‖fA，i⊗U‖1表示分量U的稀疏先验。

在JCAS 算法中，采用简单梯度算子作为分析字典。对于合成字典，采用从输入图像本身学习卷积合成字典的策略。对于式（5）是一个待优化的变量。通过矩阵乘法方式重写卷积，并对滤波器的界限加以约束，可将JCAS 算法的目标函数重写成如下形式：

其中，y、u和zj分别是Y、U和Zj的矢量化表示；FA，i和FS，i分别是滤波器fA，i和fS，i的循环块矩阵。采用变量交替更新的方式，可通过子问题（7）、（8）和（9）依次求得u、zj和fS。

式（7）和（8）是一个标准卷积稀疏编码问题，可利用文献［26］中的ADMM 方法进行求解，并结合快速傅里叶变换来提高计算效率。式（9）中，定义(fS，j⊗Zj)=FS，jzj=ΨfS，其中fS是所有滤波器的矢量化表示；Ψ=[Ψ1，…，Ψj，…，ΨN]，Ψj是从Zj中得到的补丁块。采用［27］中的近端梯度下降方法可实现（9）的求解。

3 本文方法

分量替换方法中细节信息提取和注入是影响融合图像质量的关键步骤。针对分量替换方法中光谱失真严重的问题，本文提出了一种基于JCAS算法的改进空间细节提取的遥感图像融合方法，算法框架如图1所示。整个融合过程具体步骤如下：

1）获取上采样MS 图像的强度分量I。传统IHS 算法中，只考虑利用MS 图像中的B、G、R 三个通道的光谱信息，而NIR 通道的信息并没有得到利用，使得IHS 算法获得的融合图像具有明显光谱失真。为得到更准确的I分量，采用文献［5］中的多元回归模型，可获得MS 图像各个波段的最优权重。强度分量I可通过下式获得：

其中ωi为权重系数分别表示上采样MS图像的蓝（B）、绿（G）、红（R）和近红外（NIR）谱段；ξ表示偏移量常数。

2）采用JCAS算法对I和P进行分解。首先，对强度分量I和PAN 图像进行均衡化处理，得到直方图匹配后的全色图像P，保证它们具有相同的均值信息，从而减小在融合过程中产生的光谱失真。假设强度分量I和全色图像P均由基础层和细节层构成，其可写成如下形式：

其中，Ib和Pb分别表示强度分量I和全色图像P的基础层图像；Id和Pd分别表示强度分量I和全色图像P的细节层图像。通过求解式（13）和（14）可得到最优的基础层Ib和Pb。

3）两幅细节图像获取。基础层保留了图像的大部分信息。为了尽可能地保留信息，对Ib和Pb进行加权平均得到图像Fb=0.5 ×(Pb+Ib)。由于过多细节注入会造成光谱失真，过少细节注入会造成空间细节信息损失，因此采用Fd=MAX(Pd，Id)的方式得到Fd。然后，将Fb和Fd相加得到高分辨率图像FI。将高分辨率图像FI与I分量相减获得第一幅细节图像D1，即：

传统CS 方法利用P与I分量的差作为细节信息注入到中以获得融合图像。为了弥补第一幅细节图像部分信息缺失的问题，利用式（16）构建了第二幅细节图像。

其中a用来调节D1和D2在最终细节图的占比。a的值设定为I与DI的相关系数，如下所示：

4 结果与分析

4.1 实验数据与评价方法

本文在GeoEye-1 和QuickBird 数据集中选取多组遥感图像进行了算法性能测试。GeoEye-1 卫星提供了2 m 空间分辨率MS 图像和0.5 m 空间分辨率PAN 图像。QuickBird 卫星提供了2.4 m 空间分辨率MS 图像和0.6 m 空间分辨率PAN 图像。所提供图像数据场景涉及城区、山脉、河流等，其中MS图像包含四个波段：B、G、R 和NIR。实验环境平台为：Intel（R）core（TM）i7-10700 @2.90 GHz，RAM 16.0GB，MATLAB 2018b。

评价融合图像质量的方式有两种：主观分析法和客观分析法。主观分析法通过人眼观察融合图像的光谱信息与空间结构，凭借主观感受来评价融合图像质量。该评价方法过分依赖人类视觉系统对图像质量的感知，可重复性差。因此，许多客观评价算法被提出。对于真实遥感图像数据，参考图像很难获取，所以本文采用无参考质量（Quality with No Reference，QNR）评价方法［28］。QNR评价指标由两个指标构成，分别是空间失真指标Ds和光谱失真指标Dλ。Ds、Dλ和QNR的理想值分别为0、0、1。

4.2 参数设置

本文方法JCAS 分解过程中，ASR 模型分析字典的参数M设置为7，SSR模型合成字典中N的大小设置为7。JCAS 算法中，正则参数λ和γ对算法性能具有显著影响。为了能够选择最优的正则参数，本文探讨了正则参数对算法性能的影响。图2显示了不同正则参数λ和γ对本文算法性能影响变化曲面图，其中Ds、Dλ越接近0越优，QNR越接近1越优。实验中，λ和γ的取值范围为0.01、0.1、1、10、100、1000。从图2 中可以看出，当λ和γ的取值在0.01～10范围内，本文算法的性能较优。在接下来的实验中，λ和γ分别设定为10和1。

4.3 实验结果分析

为验证本文方法的有效性，选取7 种具有代表性的融合方法作为对比算法，如：GS、PCA、基于雾度校正的加性小波亮度比例方法（Additive Wavelet Luminance Proportion with Haze correction，AWLPH［29］、基于部分置换的自适应分量替换方法（Partial Replacement-based Adaptive Component Substitution，PRACS）［6］、波段相关空间细节（Band-Dependent Spatial-Detail，BDSD）方法［30］，RBDSD（Robust Band-Dependent Spatial-Detail）［31］和基于调制传递函数匹配滤波器与高通调制注入模型的广义拉普拉斯金字塔方法（GLP with MTF-matched filter and High-Pass Modulation injection model，MTF-GLP-HPM）［32］。在GeoEye-1 和QuickBird 真实数据集上分别对本文算法和比较算法进行了性能验证。实验中采用的PAN图像大小为256×256，MS 图像的大小为64×64×4。实验采用4.1节介绍的无参考评价指标对融合图像质量进行评估。

在第一组GeoEye-1 图像上各种对比算法的融合结果如图3 所示。图3 中，（a）和（b）分别为上采样MS 图像和原始PAN 图像。图3（c）为BDSD 算法的融合结果，可以看出其具有清晰的空间细节和较好的光谱保真度。图3（d）和（e）分别为GS 和AWLP-H 算法的融合结果。AWLP-H 方法的融合图像具有较好的空间和光谱质量，但GS 方法融合图像具有一定光谱失真。图3（f）所示为PCA 算法的融合结果，其空间分辨率较高，但整体光谱失真严重。图3（g）和（h）分别为RBDSD 和MTF-GLP-HFM算法得到的融合图像。从图中可以看出，RBDSD 方法融合图像空间细节信息清晰，颜色自然。MTFGLP-HFM方法的融合图像空间分辨率较高，但其局部区域呈现非自然颜色。图3（i）所示为PRACS 算法的融合结果，其植被色彩较为自然，但空间细节有轻微模糊。本文算法融合结果如图3（j）所示，与其他对比算法的融合结果相比，该图像空间细节有少许模糊，但光谱特征较自然。

表1 给出了图3 中各种算法融合图像的客观评价指标数值结果，其中最优值标记为粗体，次优值用下划线标记。从表1 中可以看出，本文算法提供了最优的Dλ指标值，GS算法提供了次优Dλ指标值。在空间失真指标Ds方面，BDSD 算法的结果最优，RBDSD 算法提供了次优的结果。在QNR 指标上，本文算法的提供了最好的指标值，GS算法获得了次优的指标值。

表1 第一组GeoEye-1融合图像的客观评价指标Tab.1 The objective evaluation indexes of the first set of GeoEye-1 fusion results

图4 所示为第二组GeoEye-1 卫星数据的各种对比算法融合结果图。图4（a）和（b）分别为上采样MS 图像和原始PAN 图像。图4（c）为BDSD 算法的融合结果，具有清晰的空间细节和丰富的光谱特征信息。图4（d）和（e）分别为GS和AWLP-H算法的融合结果，它们的空间分辨率较高，但GS 算法的融合结果有些许光谱失真。两者对比来看，前者的房屋颜色相对较浅，AWLP-H 算法在植被区域的饱和度较好。图4（f）为PCA 方法的融合结果，其空间分辨率较低，细节信息模糊。图4（g）和（h）分别为RBDSD和MTF-GLP-HPM 算法获得的融合结果，空间细节较为清晰。但MTF-GLP-HPM 方法的融合图像整体颜色偏淡，RBDSD 的融合图像光谱信息较丰富。图4（i）为PRACS算法的融合结果，其空间细节模糊，但光谱特征较好。本文算法融合结果如图4（j）所示，与其他算法融合结果相比，其空间细节清晰，色彩与上采样MS图像相比更为接近，饱和度较高。

表2 给出了图4 所示融合图像的客观评价指标数值结果，其中最优结果标记为粗体，次优结果用下划线标记。从表2 中可以看出，本文算法提供了最优的Dλ和QNR 数值结果，BDSD 提供了最优的Ds数值结果。RBDSD 提供了次最优的Ds和QNR 数值结果，GS提供了次最优的Dλ数值结果。

表2 第二组GeoEye-1融合图像的客观评价指标Tab.2 The objective evaluation indexes of the second set of GeoEye-1 fusion results

图5 所示为第一组QuickBird 图像上各种算法的融合结果。图5（a）和（b）分别为上采样MS 图像和原始PAN 图像。图5（c）为BDSD 算法的融合结果，可以看出其具有清晰的空间细节和较好的光谱特征。图5（d）和（e）分别为GS 和AWLP-H 算法的融合结果。GS 算法融合图像具有很高的空间分辨率，但整体光谱失真严重，植被颜色相对较浅。AWLP-H 方法的融合结果具有丰富的光谱信息，但图像整体上模糊。图5（f）为PCA 算法的融合结果，其空间分辨率较高，主观性较好，但光谱特征较差。图5（g）和（h）分别为RBDSD 和MTF-GLP-HPM 算法获得的融合结果。它们具有较为清晰的空间细节和较为自然的颜色特征。相比之下后者的植被和房屋的光谱信息更好。图5（i）为PRACS 算法的融合结果，其空间信息的保留度较高。本文算法的融合结果如图5（j）所示，相较与其他对比算法的融合结果，其具有清晰的空间细节信息，颜色与上采样MS图像的颜色更为接近，色彩饱和度较高。

表3 给出了图5 所示融合图像的客观评价指标数值结果，其中最优结果标记为粗体，次优结果用下划线标记。从表3 中可以看出，本文算法提供了最优的Dλ数值结果，AWLP-H 算法给出次最优Dλ数值结果。在Ds指标上，AWLP-H 算法给出了最佳数值结果，PRACS 算法给出次最优数值结果。在QNR 指标上，AWLP-H 算法最优，本文算法为次优。

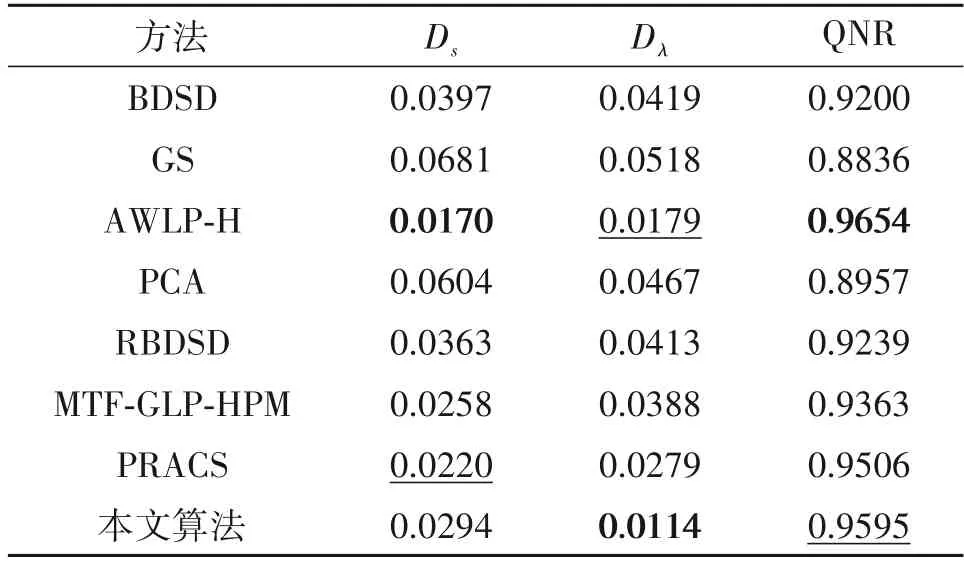
表3 第一组QuickBird融合图像的客观评价指标Tab.3 The objective evaluation indexes of the first set of QuickBird fusion results

对于第二组QuickBird 卫星数据图像，各种算法产生的融合图像如图6 所示。图6（a）和（b）分别为上采样MS 图像和原始PAN 图像。图6（c）为BDSD 算法的融合结果，具有清晰的空间细节和较好的颜色特征。图6（d）和（e）分别为GS 和AWLPH 算法的融合结果，它们的空间分辨率较高。AWLP-H 方法融合图像的光谱信息更接近原始多光谱图像，GS 方法融合图像具有轻微的光谱失真。图6（f）为PCA 算法的融合结果，其空间分辨率较高，但光谱信息丢失较多，尤其是建筑物房顶颜色失真严重。图6（g）和（h）分别为RBDSD 和MTFGLP-HPM 算法的融合结果，它们的空间细节良好，但前者的光谱信息更为丰富。图6（i）为PRACS 算法的融合结果，其空间分辨率较高，但街道区域颜色偏深。本文算法融合结果如图6（j）所示，相较于其他对比算法的融合结果，其具有较好的空间和光谱质量。

表4 给出了图6 所示融合图像的客观评价指标，其中最优数值标记为粗体，次优数值用下划线标记。从表4 中可以看出，本文算法给出了最优的Dλ、Ds和QNR数值结果。此外，MTF-GLP-HPM算法给出了次最优Ds值，PCA 算法给出了次最优Dλ值，BDSD算法给出了次最优QNR值。

表4 第二组QuickBird融合图像的客观评价指标Tab.4 The objective evaluation indexes of the second set of QuickBird fusion results

综合以上四组实验数据的主客观评价结果表明，与其他7种对比算法相比，本文算法的融合性能更为优越。

5 结论

本文针对遥感图像融合中MS 与PAN 图像光谱不匹配引起的失真问题，提出了一种基于联合卷积分析与合成稀疏表示的改进分量替换融合方法。本文方法改进了分量替换融合过程中空间细节提取和注入策略，有效地提升了融合算法性能。本文方法在GeoEye-1 和QuickBird 数据集上进行了测试。实验结果表明，该方法获得的融合结果主观评价较好，客观评价也是综合最优的。因此，本文方法可更好地消除细节信息过度注入引起的光谱失真问题，提高融合性能。

本文方法采用的JCAS 算法采用卷积操作，使得算法的时间复杂度较高。在未来的工作中，将研究更加有效的稀疏表示方法来进一步改进算法性能。此外，融合规则对融合质量起着至关重要的作用。本文所采用的融合规则相对简单，因此设计出更优的融合规则，以获得更好的融合结果也是未来的研究重点。