基于小波变换的电力系统谐波有源补偿方法研究

李仕杰

(国网浙江海宁市供电有限公司，浙江 嘉兴 314400)

电力系统谐波是指与交流电网中有效工频频率存在差异的成分，其产生的原因是正弦电压对非线性负载加压，电流从非线性负载通过时，和施加电压之间呈现非线性关系，导致基波电流产生畸变[1]。电源自身产生的谐波、输配电系统产生的谐波以及用电设备产生的谐波是电力系统谐波产生的三种情况，其中，电力设备产生的谐波是当下电力系统的主要谐波[2]。谐波的产生会对电网电压、线路使用寿命、电缆可通过的最大电流造成较大影响，并且会引起电力保护元件的损坏以及继电保护的误动作[3]。为避免上述问题的出现，保证电网的安全运行，需要实行谐波控制和管理。

小波变换是一种具备短时傅里叶变换局部化功能的新的一种变换分析方法可有效避免频率变化时窗口大小没有变化的现象。其主要特点是将问题的部分特征通过变换后显著化，局部化分析时间(空间)频率，并利用相关算法对信号实行多尺度细化处理，完成高频处和低频处的时间细分，有效处理信号问题，因此其在多个领域均被广泛应用[4]。因此，针对电力系统谐波有源补偿问题，需要一种能够精准检测谐波含量、并且具备针对性的实时补偿方法，本文提出基于小波变换的电力系统有源补偿方法，利用有源电力滤波器有效完成电力系统谐波的治理，并实现谐波补偿，保证电力设备的正常使用以及系统的安全运行。

1 基于小波变换的电力系统谐波有源补偿方法

1.1 电力系统谐波有源补偿原理

并联电压型电力系统结构见图1，其由指令电流预算电路和补偿电流发生电路组合形成。

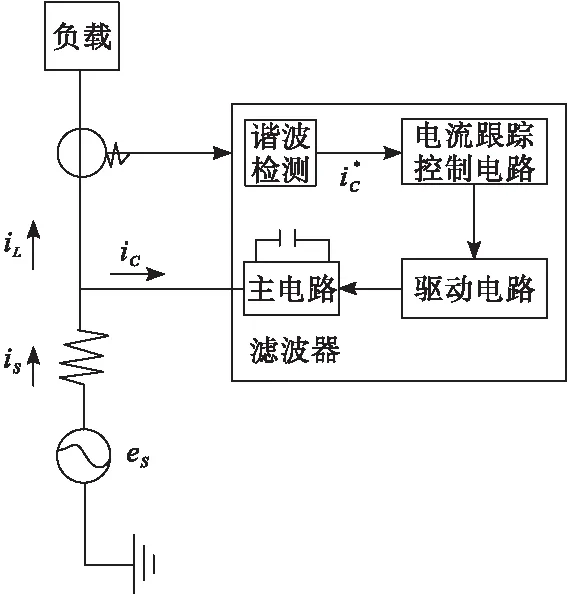
图1 并联电压型电力系统结构

图1中电网电压源、交流电网电流、负载或者补偿对象电流、补偿电流的表示参数分别为es、is、iL、iC。谐波源负载产生谐波，并对无功功率实行消耗。

1.2 基于小波变换的谐波检测

为实行电力系统的谐波补偿，需完成谐波检测。本文采用小波变换完成电力系统的谐波检测。为更精准的检测谐波，将塔式算法与小波变换相结合，先完成离散信号的分解后再进行检测[5]。其分解公式为

(1)

式中：t和f(t)分别为离散时间序号和原始信号，且t=1，2，…，N；Aj和Dj分别为信号在第j层低频部分的小波系数和高频部分的小波系数，且j=1，2，…，J，J=log2N；H和G分别为小波分解低通滤波器和带通滤波器。

根据式(1)可知：离散信号f(t)在第j层的低频部分和高频部分的小波系数的获取，分别通过第j-1层的低频部分和高频部分的小波系数，分别与分解滤波器H和G实行卷积，并完成隔离点采样得出。分解后可将上一层低频部分的小波系数分解成低频部分和高频部分的小波系数[6]，其分解算法原理用图2描述。

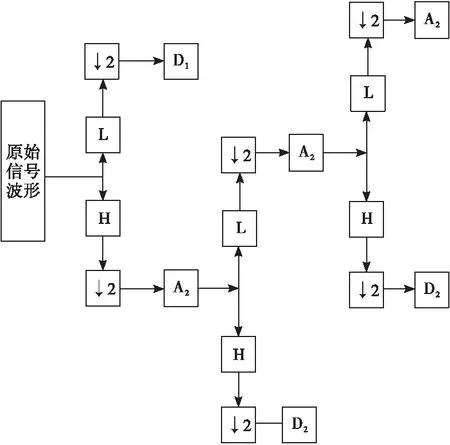
图2 塔式算法分解原理

分解算法的逆过程为重构算法，其公式为

(2)

式中：h和g分别为时域中的小波重构滤波器。

根据式(2)可知：结合第j+1层的低频部分和高频部分的小波系数隔点插零后，分别和重构滤波器h和g的卷积，可获取信号在第j层高频部分的小波系数。重复上述步骤直至获取重构信号[7]。

假设用iL(t)为滤波器检测到的包含谐波的负载电流信号，根据不同频率对其分量，公式为

(3)

式中：{AJ1k}具备有限长度NJ1。

为使信号分解成不同的通道成分，采用塔式算法即可完成，其公式为

(4)

式中：AJ2f(t)为频率低于2-J2的信号成分；Djf(t)为f的频率介于2-j和2-(j-1)之间的成分，且Djf(t)=∑Djkψjk。

信号基频成分可通过重复上述步骤完成分离，所有谐波成分的获取可通过原始信号减去基频成分的差表示。

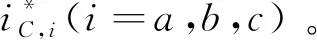
1.3 电流跟踪预测控制方法

1.3.1 流压转换

由于改进空间矢量脉宽调制控制策略可以较大程度地提升逆变器直流侧电压的利用率，因此将其用于电力系统跟踪预测中。

跟踪获取的参考电压值通过控制三相逆变器的实际输出完成，在此之前需确定参考电压矢量[9]。电力系统输出电压和电网电压分别用u和uS表示，两者之间的关联性用式(5)表示：

(5)

式中：iC和R分别为电力系统输出的电流矢量和输出端滤波电感的等效电阻。将式(5)实行离散化处理后得出：

(6)

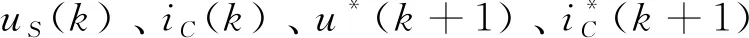
1.3.2 电流预测控制

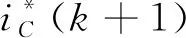
(7)

(8)

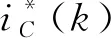
由于很多负载电流在实际应用时的周期性变化不快，所以可以对参考电流实行预测。上述预测方法为开环控制方法，预测会存在一定误差，因此将校正量引入方法中避免误差[12]，其方法流程如图3所示。

图3中，Z、k分别表示变换算子和稳定系数；Z-1和Z-N+1分别表示滞后1个和-N+1个采样周期；e(k)表示电力系统当前输出电流的实际采样值和上一拍的预测值之间的误差；ΔiC和iref(k+1)分别表示最后校正量和校正后的预测参考电流值，其计算公式为

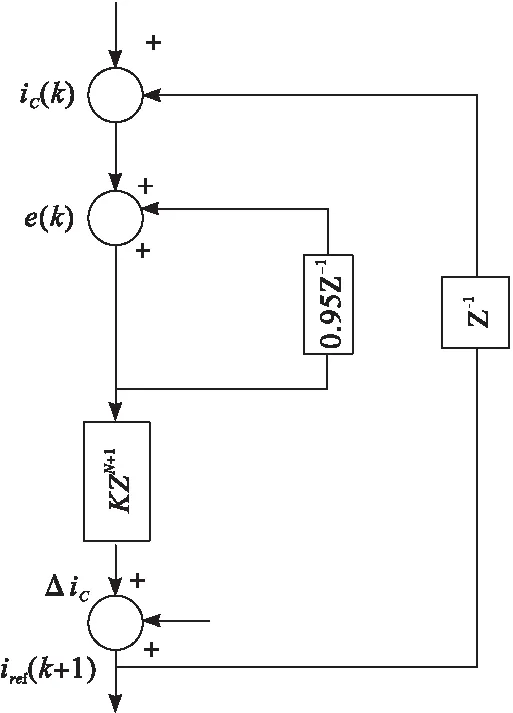
图3 预测方法流程

(9)

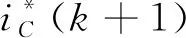
系统暂态情况下的判断方法为

e(k)=|iC(k)-iC(k-N)|iref(k+1)≥emax

(10)

式中：emax为相邻的两个基波周期同一采样时刻电流变化的误差阈值。

综上所述：流压转换和消除数字信号离散化导致的周期性延时，均可通过下一采样周期的参考电流值的预测完成；三相逆变器实际输出电压跟踪参考电压的获取，通过改进空间矢量脉宽调制控制策略完成[14-15]，实现电力系统谐波补偿。

2 测试分析

为测试本文方法的应用效果，以某电力系统的三相桥式整流电路为实例研究对象，采用Matlab 软件和PSCAD/EMTDC以真实数据进行仿真实验。模拟电力系统的相关参数如表1所示。

PSCAD/EMTDC仿真获取的三相桥式整流电路的负载电流波形和频谱分析结果，用图4、图5描述。

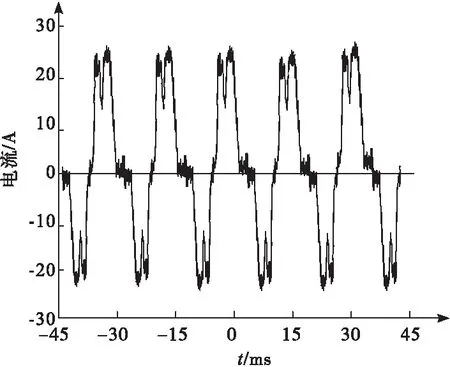
图4 负载电流波形

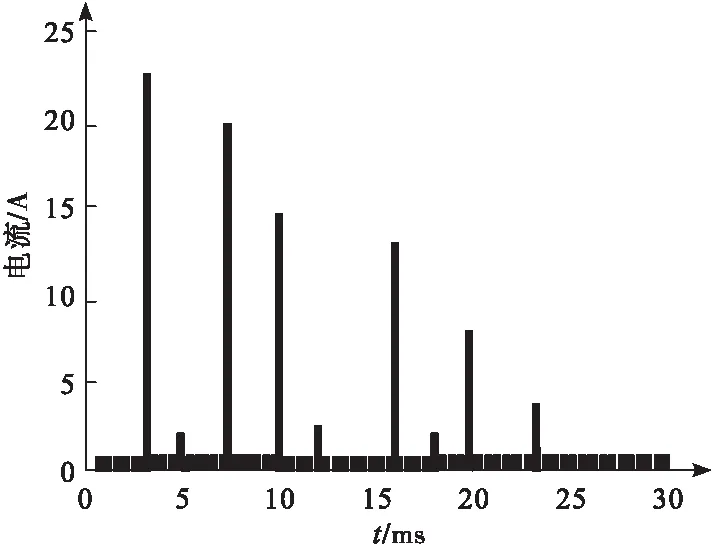
图5 频谱分析结果

将PSCAD/EMTDC仿真获取的电流数据导入Matlab软件中，进行仿真分析。根据表1中参数设置进行采样，共采集600个点，采用本文方法对其进行谐波检测。先对采集的信号进行小波分解，获取分解后的不同层的近似部分重构信号波形，结果用图6描述。

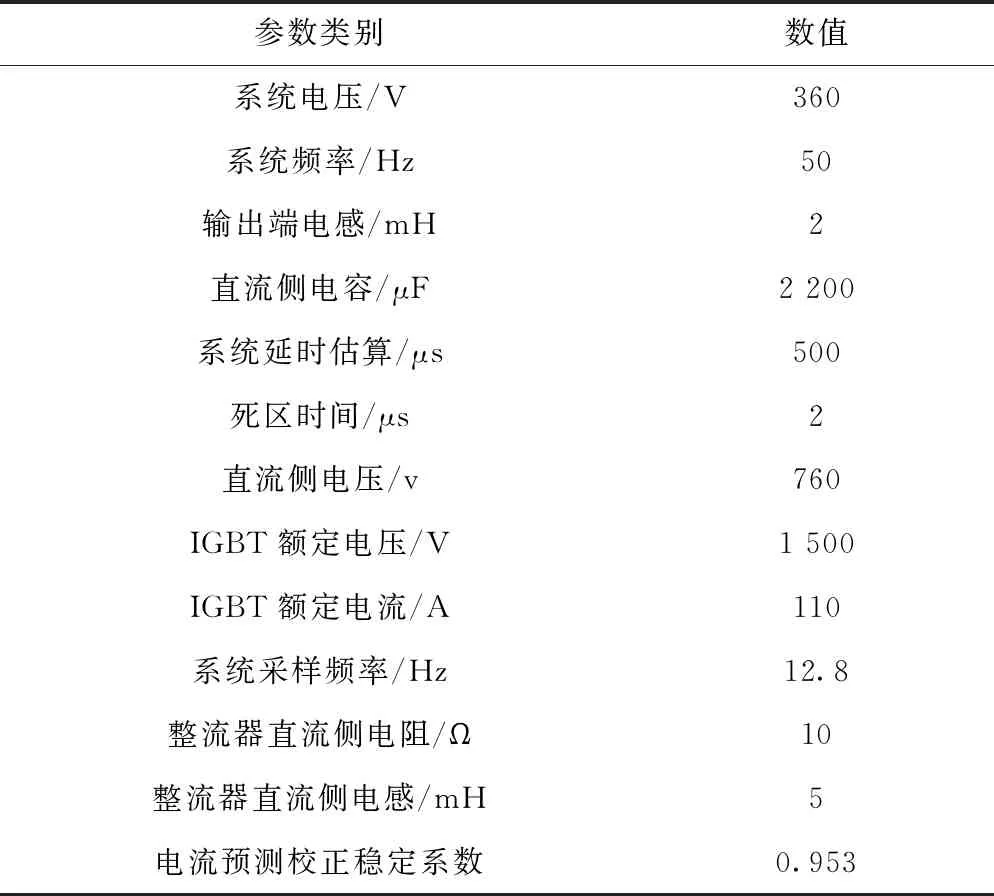
表1 电力系统相关参数

根据图6测试结果可知：采用本文方法进行谐波检测时，对信号进行分解，在分解第4层时，就可获取基频波形，并且分解4层后的近似部分重构信号，即为负载电流中的基波成分。把负载电流减去信号分解后的负载电流中的基波成分，即可得到系统需产生的电流。该结果表明本文方法可有效地完成谐波检测。

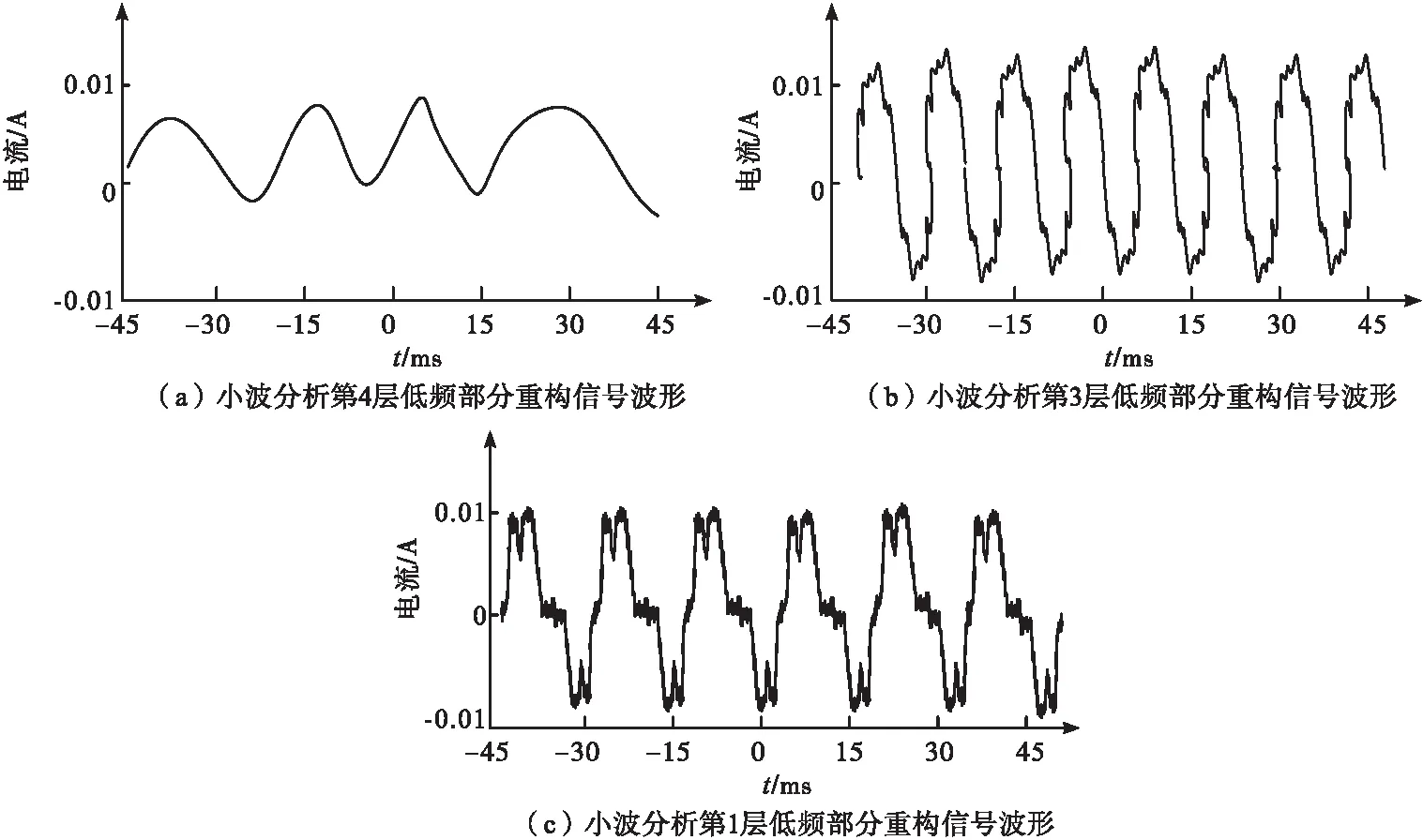
图6 不同层的近似部分重构信号波形

谐波检测后，采用本文补偿方法和传统补偿方法对电力系统电流进行预测，并将补偿后的预测结果与实际的参考电流值进行对比，对比结果如图7所示。

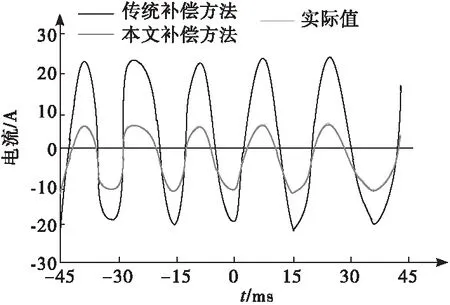
图7 电力系统电流预测结果对比图

根据图7可知，本文补偿方法预测的电力系统电流值与实际的参考电流值误差较小，而传统补偿方法预测的电力系统参考电流值与实际的参考电流值误差较大，是因为本文为使预测值接近实际值，通过不断调整校正量完成，缩小了电力系统电流预测误差，说明本文方法的电力系统谐波有源补偿效果较好。

3 结 论

电力系统中谐波的产生会对电力设备以及电网的安全运行造成一定影响。为避免谐波造成的影响，本文研究基于小波变换的电力系统谐波有源补偿方法。并通过模拟实验进行方法验证，结果表明：本文所研究的方法可有效完成电网谐波的检测，并且补偿后的电网电流预测值与实际值误差较小。

本文方法具备上述优势的同时，下述几点则需要进一步的研究和完善：

(1)当电网电流的负载谐波含量不固定时，如何采用本文方法进行有效补偿，需要进一步研究和测试。

(2)如何利用本文方法在待补偿谐波次数不固定时，确定谐波次数并准确完成谐波补偿，也是本文下一步需要研究的内容。