固态流化单喷嘴破碎水合物深度预测新模型及验证

余兴勇 钟 林, 王国荣, 李绪深 方小宇 张计春

1. 西南石油大学机电工程学院 2. 南方海洋科学与工程广东省实验室（湛江）

0 引言

天然气水合物（以下简称水合物）作为一种高能量密度的天然气能源，极具开发价值，若成功开发可助力我国“碳达峰、碳中和”战略目标[1-4]。我国的水合物资源主要分布于南海，2020年，在南海神狐海域实施第二轮水合物试开采，平均日产气量为 2.87×104m3，30 天总产气量达 86.14×104m3，充分证实了南海海域具有巨大的水合物资源潜力[5]。但该区大部分为非成岩水合物，具有埋藏浅、弱胶结、无致密盖层等特征，规模化开采面临地质、设备和环境三大风险[6-7]，采用现有的热激法、CO2置换法或降压法等仍未从根本上解决开采过程中出现的储层坍塌、海底滑坡等灾害[8-9]。为此，周守为等[10]提出了针对非成岩水合物开采的固态流化法，该工艺利用水射流将储层流化破碎成浆体，并利用举升泵输送至海面进行分解，整个开采过程维持水合物在储层中的相态稳定，可有效降低开采风险。2017年5月，固态流化法在南海神狐海域的试采中证明了其技术上的可行性[11-12]，但该方法由于存在采掘效率低的问题，现阶段还无法实现商业化应用。

射流破碎作为固态流化法的核心技术，其效率直接决定了该开采方法的效率。Wang等[13]研究了水合物饱和度、喷射压力和喷嘴直径对最终破裂距离的影响，建立了海洋水合物水射流破碎临界速度的计算公式；王国荣等[14-15]开展了水合物固态流化采掘破碎参数的初步优化设计，但并未提出喷嘴的设计依据；董宗正等[16]针对圆柱形、锥直形及圆锥形流道喷嘴，开展了射流流场仿真分析，得到高压射流时的最佳喷嘴流道结构为锥直形；杨国来等[17]针对锥形及锥直形喷嘴开展了高压水射流流场速度、压力等的数值模拟研究，得到长径比为2～3时锥直形喷嘴的射流速度最佳；Liao等[18]通过数值模拟得出收敛角度为13°、圆柱段长度为8 mm、喷嘴出口直径为2 mm的锥直形喷嘴在水力切割方面具有最好的综合效果。目前，在射流破岩领域锥直形喷嘴是常用的单喷嘴结构之一，但针对水合物储层破碎的设计理论仍未见相关报道，严重阻碍了射流破碎工艺参数的优化与高效开采工具的研制。

为提高射流破碎效率，推进我国水合物开采的规模化进程，笔者根据已优选的锥直形喷嘴，开展了单喷嘴压力、收缩段长度和直径的仿真分析，研究流速分布特征，初步建立了水合物射流采掘单喷嘴极限破碎深度数学模型。在此基础上，利用已开展的实验数据对模型进行了验证和修正，以期为海洋非成岩水合物高效射流破碎工具研发及工艺参数的制订提供支撑。

1 流场模拟与模型建立

1.1 物理描述

1.1.1 喷嘴结构及几何模型

笔者以锥直形喷嘴为研究对象，其外形及结构如图1所示。其中主要参数包括收缩角α、喷嘴直径d0、喷嘴总长度L、喷嘴圆柱段长径比L1/d0。相关几何参数如下：收缩角α经本文参考文献[18]研究得出13°时射流切割效果最好，喷嘴总长度依据固态流化开采工具管串参数[19]设计为12 mm。

图1 锥直形喷嘴外形及结构图

1.1.2 喷嘴射流结构特性

图2为淹没射流结构示意图，喷嘴射流结构主要分为初始段、转折段和基本段。射流在初始段有一个速度保持不变的区域，称为射流核心区，其长度记为核心段长度[20]。初始段在工业中主要用于切割，段内核心段长度越大，对水合物的破碎效果越好。过渡段为初始阶段和基本段的中间区域，其间射流方向及速度的大小都会发生突变，该区域一般较小，通常在计算分析中不予考虑。基本段内射流的径向截面上流速呈高斯曲线分布，而轴向流速及动压值都会按一定的规律下降，直至速度为0并与环境介质完全融合，基本段的轴向速度衰减越小，对水合物储层的破碎距离越长，破碎体积越多。

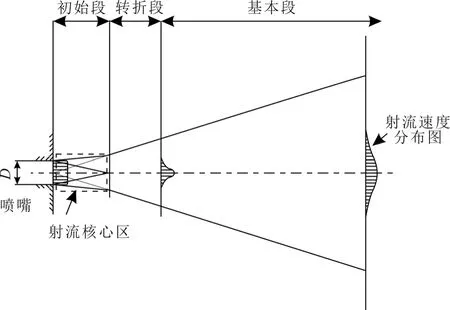
图2 淹没射流结构示意图[20]

1.2 数值计算模型及方法

为了研究锥直形喷嘴流速的分布特征，笔者对不同喷嘴直径、不同射流压力以及不同喷嘴收缩段长度进行了仿真。由于实际固态流化对水合物的破碎过程中，工况十分复杂，综合考虑计算机和时间成本，对模型进行了以下简化：①锥直形喷嘴射流为连续均质流体；②固态流化开采的过程中水合物相态稳定，忽略气水饱和度对射流的影响；③不考虑射流空蚀。

采用计算流体软件Fluent对锥直形喷嘴开展数值模拟研究，几何模型及网格如图3所示。利用ICEM CFD进行网格划分，为兼顾计算效率和精度采用结构化网格，计算区域进行分割处理，对核心射流区域的网格进行了加密。为研究单个锥直形喷嘴关键参数，外流场的直径为50 mm，长度达500 mm[21]，喷嘴入口边界采用压力入口，外流场出口边界采用压力出口。

图3 几何模型及网格图

喷嘴射流数值计算模型控制方程包含连续性方程、Navier-Stokes方程，湍流模型采用标准k-ε模型[22]。为提高计算精度，对流场求解各方程均采用二阶迎风格式。假设流体为不可压缩流体，且在射流过程中无热传导发生，基本控制方程组如下。

根据固态流化工艺对水合物破碎的需求，本文所选取锥直形喷嘴及射流参数见表1。

表1 喷嘴及射流参数表

1.3 锥直形喷嘴关键参数分析

针对锥直形喷嘴，基于水合物射流破碎临界速度，分析了射流压力、收缩段长度及喷嘴直径对射流速度分布的影响，推导轴心速度衰减与喷嘴直径、压力、收缩段长度等关系式，最终建立了水合物射流破碎所用喷嘴的设计公式。

1.3.1 射流压力影响

在喷嘴直径2 mm、收缩段长度6 mm、圆柱段长径比3的情况下，分别模拟了射流压力为5.0 MPa、7.5 MPa、10.0 MPa、12.5 MPa 和 15.0 MPa 的流场状况，得到了喷嘴轴心速度的衰减规律及核心段长度的变化规律。由图4可知，随着射流压力的不断增大，喷嘴的出口速度有所提升，但是射流核心段的长度基本不发生变化。同时，由于压力的增大，射流基本段速度衰减的速率减小。

图4 不同压力下喷嘴轴心速度衰减规律及核心段长度变化规律图

1.3.2 收缩段长度影响

在喷嘴直径2 mm、射流压力5 MPa、圆柱段长径比3的情况下，分别模拟了收缩段长度为1 mm、2 mm、3 mm、4 mm、5 mm 和 6 mm 的流场状况。由图5可知，喷嘴收缩段长度的改变对外流场轴心速度衰减几乎没有影响，随着收缩段长度的增加，射流轴心速度的衰减规律基本一致，射流核心段长度基本一致。

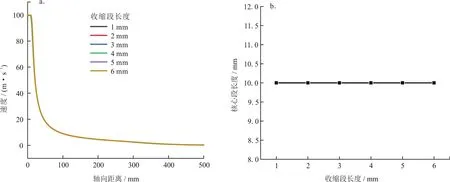
图5 不同收缩段长度下喷嘴轴心速度衰减规律及核心段长度变化规律图

1.3.3 喷嘴直径影响

在射流压力5 MPa、收缩段长度6 mm、圆柱段长径比3的情况下，分别模拟了喷嘴直径1～10 mm的流场状况。从图6中可以看出，随着喷嘴直径的增大，射流核心段长度不断增加，射流基本段的速度衰减率逐渐减小。

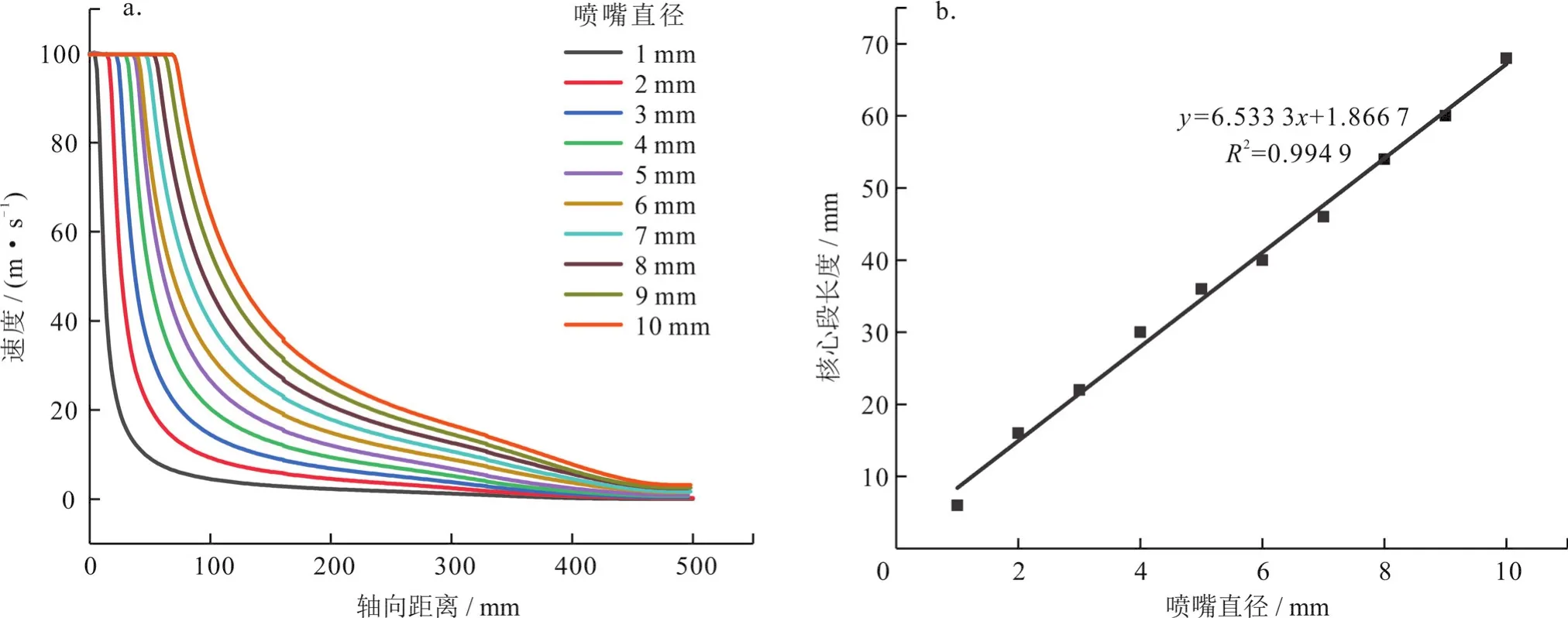
图6 不同直径下喷嘴轴心速度衰减规律及核心段长度变化规律图

1.4 喷嘴设计计算公式

在对锥直形喷嘴关键参数分析的基础上，得出锥直形单喷嘴外流域速度主要受到喷嘴直径和射流压力的影响，其中射流压力主要影响出口初速度，故将射流压力转换为出口初速度进行分析。为进一步对喷嘴外流域轴心速度衰减规律进行描述，定义Y=νx/ν0，X=d0/x，其中νx表示喷嘴轴心线任意位置x的速度，m/s；d0表示喷嘴直径，mm；ν0表示出口初速度，m/s；x表示喷嘴轴心线距离，mm。对1.3节数据整理可得图7，从图7中可以看出，X—Y关系曲线图呈“厂”字形分布，水平段为射流核心段，喷嘴直径增大，直线段越长即核心段越长，这在前面已有描述；折线段则为射流基本段及发散段，喷嘴直径的增加使得折线段的斜率不断增大即核心段后速度衰减越大。

图7 X—Y关系曲线图

为了获取单喷嘴破碎深度，需要求取其任意位置轴心速度，采用Boltzmann函数对喷嘴轴心线任意位置速度进行拟合，Boltzmann函数模型如式（6）所示，由于本文为单向射流，故只取Y＞0的部分。

式中A、C分别表示轴心速度相关的无量纲参数；B表示射流轴心最大速度与理论出口速度的比值；D表示轴心速度随距离的变化速率。通过仿真数据对各系数进行标定，系数A与喷嘴直径呈反比例关系，其关系如图8-a所示，B= 1.023，C= 0.07，D= 0.038。

图8 系数A、B、C、D随喷嘴直径和射流压力的变化关系图

综上，将系数A、B、C、D和Y=νx/ν0、X=d0/x带入式（6），又因为可知喷嘴出口的初速度ν0与射流压差有关，将该式一并带入后整理得到自由淹没射流条件下，喷嘴外流域轴心速度的分布与喷嘴直径及压力的变化规律关系式。

式中Δp表示射流压力，MPa；ρ表示水的密度，1 000 kg/m3。

结合固态流化开采，假设忽略射流过程中返排作用的影响，射流破碎均为射流束作用于水合物壁面而产生，且射流时间足够长时，则当单喷嘴在进行水合物射流采掘达到射流破碎临界速度时，水合物采掘的破碎深度将达到理论最大值，即已知νx=ν临界，则可在射流压力和喷嘴直径确定的条件下，推断出水合物射流采掘的理论最大深度xmax，其中ν临界由本文参考文献[13]的水合物临界破碎速度公式求得，如式（8）所示；反之，若要求在射流压力确定的条件下达到所需要的破碎半径，可以反推喷嘴直径。故将上式变形为喷嘴直径与喷嘴出口距离、射流压力的关系式，见式（9）。该公式适用于固态流化非成岩水合物开采情况下针对特定破碎半径获取对应喷嘴直径。

式中ν临界表示水合物临界破碎速度，m/s；η表示特征速度，m/s；patm表示大气压力，MPa；φ表示内摩擦角，取值33.8°；c0表示内聚力，为0.3 MPa；α和β表示常数，分别为4.64×10－3和1.58；Sh表示水合物饱和度；xmax表示最大破碎深度，mm。

2 模型验证及修正

为了进一步验证公式的实用性，根据本文参考文献[13]的实验数据进行了验证。实验变量包含了饱和度、喷嘴直径和射流压力，其中饱和度主要影响临界破碎速度，其余参数都与本文所提出的射流关键参数相同。

2.1 破碎深度对比分析

2.1.1 不同饱和度下破碎深度

图9-a为不同饱和度对破碎深度的影响（饱和度20% ～80%，p=5 MPa，d0=2 mm），从图中可以看出，当喷嘴直径和射流压力一定时，随着水合物饱和度的增加，破碎深度在射流的作用下逐渐减小，总体上破碎深度随饱和度的增长在一定程度上逐渐减小。其原因是饱和度增加，水合物的胶结强度增强，导致破碎效果减弱，并且这种强度的增加并非线性增强而是趋势逐渐加快，说明了预测模型中xmax和ν临界的幂函数关系是切合实际的。

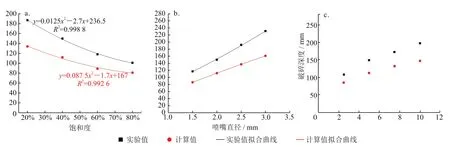
图9 破碎深度对比分析图

2.1.2 不同喷嘴直径下破碎深度

图9-b为不同喷嘴直径对破碎深度的影响（d0=1.5 ～ 3.0 mm，饱和度 40%，p=5 MPa），从图中可以看出，当饱和度和射流压力一定时，随着喷嘴直径的增加，破碎深度逐渐增加，图中可以看出破碎深度随喷嘴变化规律存在线性关系，与预测模型中xmax和d0近似的线性关系的符合度较高。原因是射流压力一定时，喷嘴直径的增加会导致射流出口流量增加，从而使射流能量增大。

2.1.3 不同射流压力下破碎深度

图9-c为不同射流压力对破碎深度的影响（p=2.5 ～ 10.0 MPa，饱和度 40%，d0=2 mm），从图中可以看出，当喷嘴直径和饱和度一定时，随着射流压力的增加，破碎深度逐渐增加，但变化趋势有所减小，因为压力增加导致射流速度加快，使得破碎深度更大。

2.2 单喷嘴尺寸计算模型优化和准确性校核

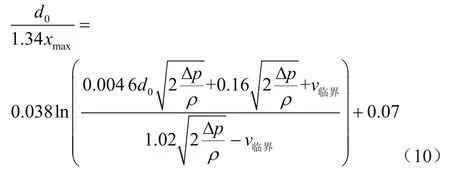
由上述分析可以看出预测模型计算值与实验值的趋势是一致的，但是因为该模型针对理想流场进行推导，忽略了实际工况中存在的诸如破碎腔壁面等因素对流场的影响，故与实验值存在一定误差。为了修正上述误差，在公式中引入了修正系数，结合实验值求得该系数为1.34，修正后的公式如下，并利用修正后的公式计算值与试验对比，以进一步验证模型准确性。

2.2.1 不同饱和度下破碎深度校核

在压力为5 MPa、喷嘴直径2 mm的情况下，通过修正公式计算和实验值得到的破碎深度如图10-a所示，在饱和度20%、40%、60%和80%的情况下，对应的理论值和实验值之间的绝对误差分别为6.99 mm、0.45 mm、1.56 mm、7.81 mm，相对误差分别为 3.74%、0.30%、1.32%、7.73%，误差最大值出现在饱和度为80%处，绝对和相对误差为7.81 mm和7.73%。

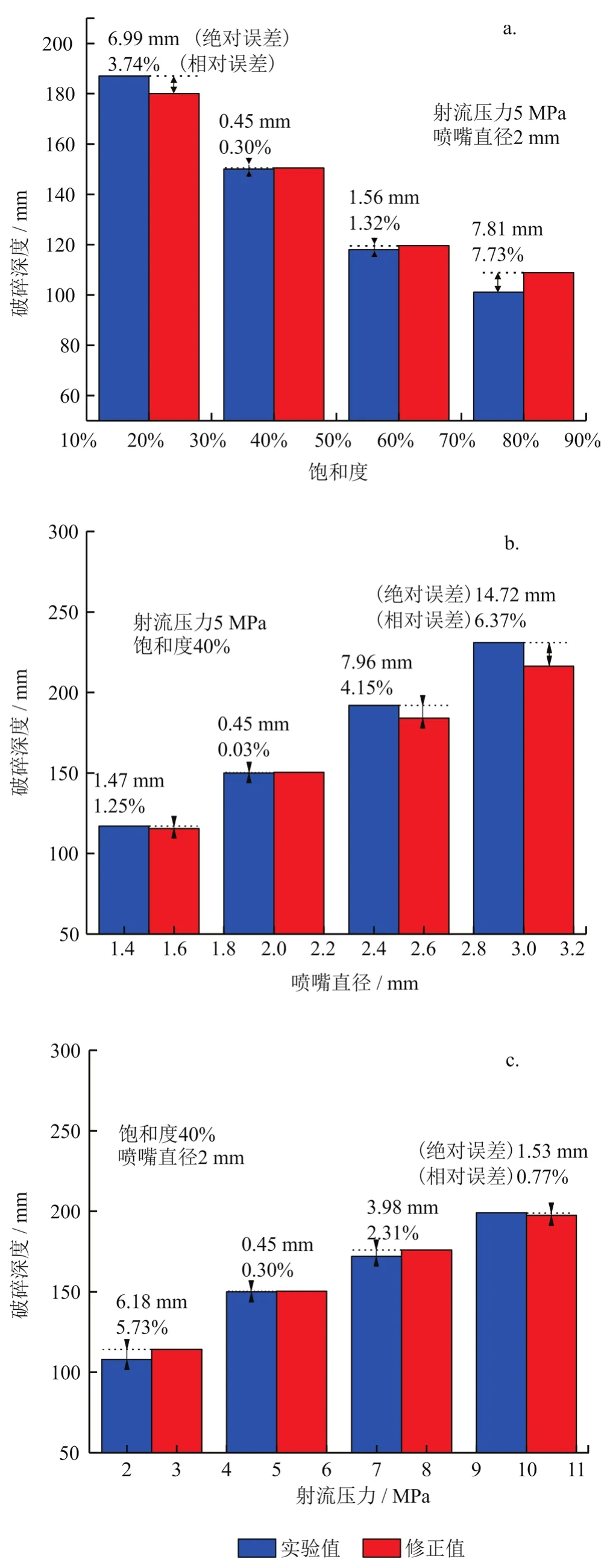
图10 模型优化和准确性校核图

2.2.2 不同喷嘴直径下破碎深度校核

在压力为5 MPa、饱和度为40%的情况下，通过修正公式计算和实验值得到的破碎深度如图10-b所示，在喷嘴直径为 1.5 mm、2.0 mm、2.5 mm 和3.0 mm的情况下，对应的理论值和实验值之间的绝对误差分别为 1.47 mm、0.45 mm、7.96 mm、14.72 mm，相对误差分别为1.25%、0.03%、4.15%、6.37%，误差最大值出现在喷嘴直径为3.0 mm处，绝对和相对误差为14.72 mm和6.37%。

2.2.3 不同射流压力下破碎深度校核

在喷嘴直径为2 mm、饱和度为40%的情况下，通过修正公式计算和实验值得到的破碎深度如图10-c所示，在射流压力表示 2.5 MPa、5.0 MPa、7.5 MPa和10.0 MPa的情况下，对应的理论值和实验值之间的绝对误差分别为 6.18 mm、0.45 mm、3.98 mm、1.53 mm，相对误差分别为5.73%、0.30%、2.31%、0.77%，误差最大值出现在压力为2.5 MPa处，绝对和相对误差为6.18 mm和5.73%。

综上，通过对比修正公式计算的结果与实验值最大偏差约为7.7%，但由于本文是为固态流化实际工程中水合物破碎提供工具设计依据，该偏差是能够满足实际工程要求的，故该水合物射流破碎单喷嘴尺寸设计公式是合理的，可为水合物射流采掘单喷嘴设计提供理论依据。

3 结论

1） 锥直形喷嘴射流核心段长度主要与喷嘴直径呈正相关关系，而与射流压力、收缩段长度基本无关；射流基本段速度衰减与喷嘴直径和射流压力呈负相关，而与收缩段长度无关。

2）基于水合物射流破碎临界速度，初步建立了极限破碎深度随喷嘴直径和射流压力变化的数学模型，并依据已开展的不同饱和度、不同喷嘴直径和不同射流压力的实验结果进行对比，验证了模型与实验结果具有相同的趋势。

3）根据实验数据进行了模型在实际工况下的误差矫正，修正后模型与实验数据间的最大误差为7.7%，为水合物射流破碎单喷嘴尺寸设计及评价提供了理论依据。

4）在单喷嘴极限破碎深度模型的基础上，下一步将发展到组合喷嘴极限破碎深度模型的研究，分析多个喷嘴组合情况下布置夹角和布置间距对极限破碎深度的影响，最终形成一套水合物高效破碎工具设计方法，以期推动固态流化工艺规模化、商业化发展。