原子系综在二次方相互作用演化下多体纠缠特性
王娅妮,王明锋
(温州大学 数理学院,浙江 温州 325035)
量子纠缠在研究多体系统方面有着极其重要的作用[1-3],其作为一种量子资源已被广泛应用于量子信息的处理过程[4-6],例如量子计算[7-8]、量子隐形传态和量子通信等方面[9-13]。除此之外,在对量子力学中的一些非经典现象进行研究时发现,量子纠缠在量子调控方面也扮演着不可替代的角色。正是因为这些原因,量子纠缠各种性质的研究越来越受研究者的关注。在多体系统中,量子相变会改变粒子之间相互纠缠的方式[14]。Lipkin-Meshkov-Glick模型是最简单的自旋与量子系统发生相变的相互作用模型,可以使得两粒子纠缠发生相变[15-16]。当两粒子纠缠变成多粒子纠缠之后,纠缠现象就会从微观纠缠变成宏观纠缠[17-18]。目前,纠缠已经在各种系统中实现,且已有多种方案用于制备原子系综的纠缠态。其中一种是光场记忆法[19],即将纠缠光子标记到原子系综上实现原子间的纠缠;另外一种是投影测量法[20],通过对与原子相关联的量子光场实施测量即可将光与原子间的纠缠通过纠缠交换转换成原子间的纠缠;第三种是非线性相互作用法,就是利用非线性演化哈密顿量制备量子体系的多体纠缠[21-22]。在非线性演化方法中,单轴扭曲相互作用是实现多体纠缠的重要手段,已经被广泛地应用于自旋压缩[20,23]。迄今为止,对于单轴扭曲相互作用的研究,聚焦点主要在如何实现对量子体系的高度自旋压缩,并未对产生的多体纠缠性质进行过深入研究。本文研究在单轴扭曲相互作用下原子体系的多体纠缠特性,应用平均量子Fisher信息对体系的多体纠缠进行度量。平均量子Fisher信息是一种度量多粒子纠缠的重要衡量手段,已经在理论和实验上被广泛地研究。通过计算体系的平均量子Fisher信息,发现在单轴扭曲哈密顿量作用下产生的量子态具有高度的量子纠缠特性。在此基础上,我们研究了附加线性相互作用演化下体系的多体纠缠特点,发现线性相互作用可极大地延长纠缠的时间,更加有利于多体纠缠在量子精密测量领域的应用。最后,我们也考虑了在外场波动下,体系的多体纠缠演化特性,发现即便存在外场波动,其量子纠缠度依旧很大。
1 单轴扭曲演化下的自旋压缩及量子纠缠特性

(1)

S+(t)=eitF(Sz)S+(0)e-itF(Sz)=S+(0)eitF(Sz+1)e-itF(Sz)=S+(0)eitf(Sz),
S-(t)=[S+(t)]†,
(2)

(3)
因为自旋极化沿着x轴,所以Sy,Sz的期望值为:
(4)
为了方便计算各自旋分量平方的期望值,我们将自旋分量的平方展开,先计算其各部分的期望值最后再将其加起来得到总的自旋分量平方期望值:
(5)
系统3个自旋分量的方差由〈ΔS〉2=〈S2〉-〈S〉2给出,综上可得各分量上方差为[21]
(6)
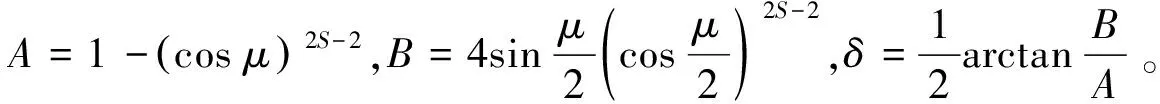

(6)
通过代入前面的结果可得
(7)

2 单轴扭曲和线性演化协同作用下的量子态纠缠特性


图1 N=40时,单轴扭曲演化下量子态在布洛赫球上的准概率分布图

图2 N=40时,单轴扭曲和线性项共同演化下的量子态在布洛赫球上的准概率分布图

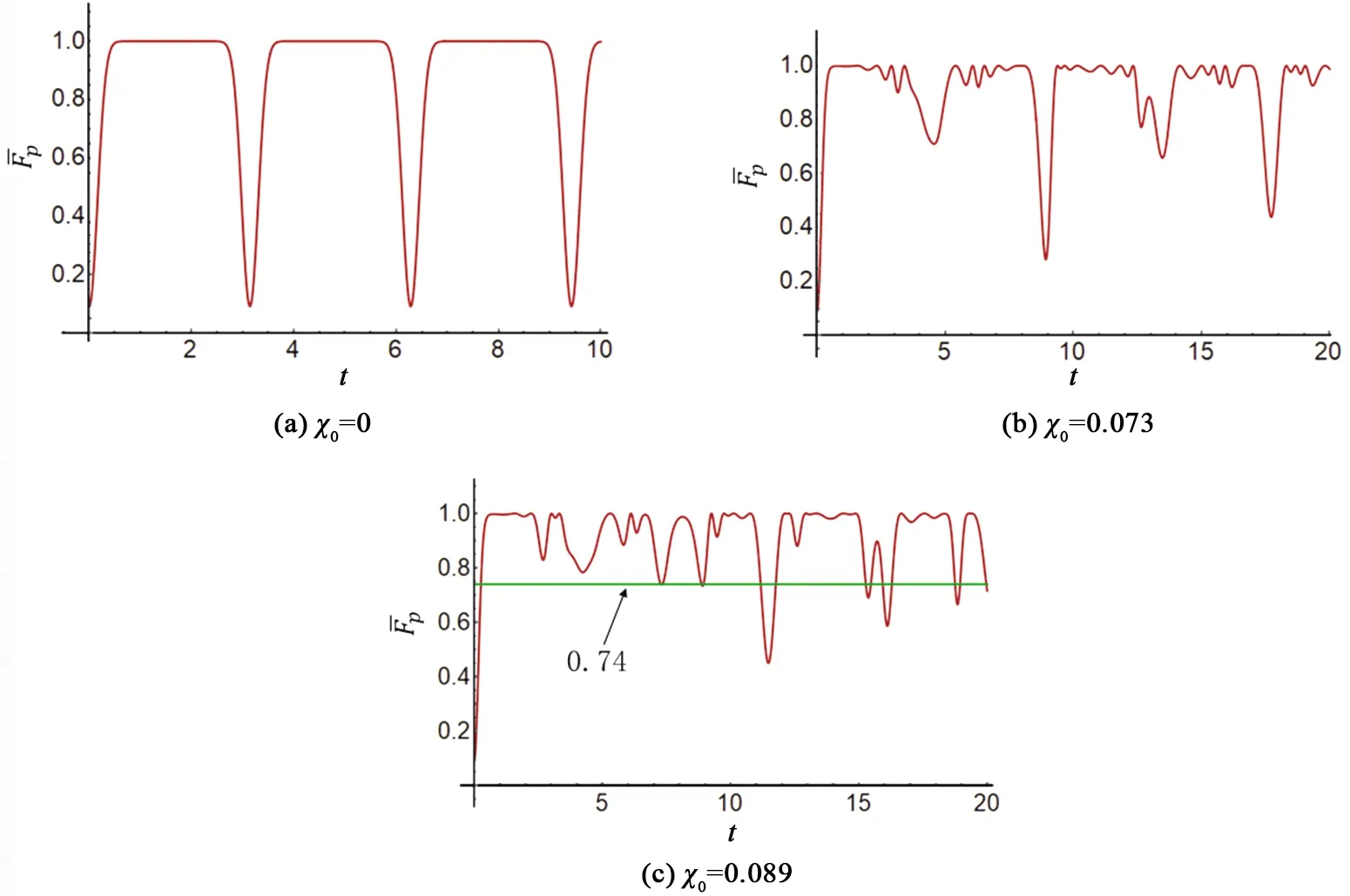
图3 理想情况下不同χ0对应的平均量子Fisher信息随时间t变化的图像
3 噪声对方案的影响
(8)

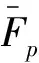
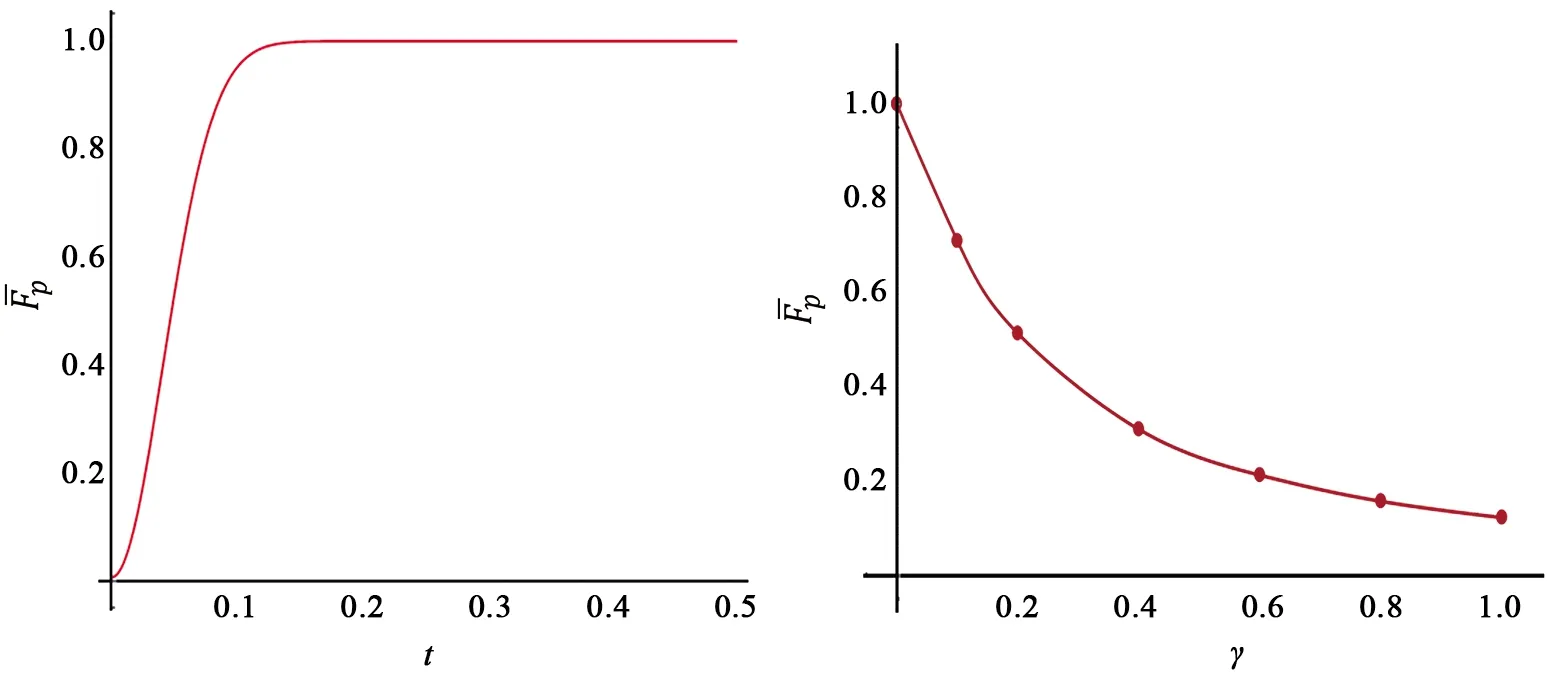
(a)理想情况下随时间t的变化最大值随不同退相干系数γ的变化
4 结论
本文研究了在原子系综单轴扭曲演化下产生的压缩态之间多体纠缠的特性问题,通过结果呈现出本方案除了产生很好的压缩特性,能达到海森堡极限之外,其原子之间产生的纠缠特性也是比较好的,在很短的时间内就达到了量子纠缠的最大值并可以保持相对较长的时间。其次,利用数值模拟研究了在原子系综中线性和非线性共同作用下自旋体系产生的量子态的纠缠特性问题。发现了线性相互作用可极大地延长纠缠的时间,在某些值下,量子纠缠虽有小波动,但总体在很长时间内都保持在较大的值,可以更广泛地应用于量子精密测量和量子隐形传态。并且发现在有外场波动的情况下,依旧会保持很好的纠缠性质,本方案对于量子测量的实际应用可以起到很好的效果。

