图形、图像融合利用的集成学习智能化简方法及其在岛屿岸线化简中的应用

杜佳威,武 芳,朱 丽,刘呈熠,王安东

信息工程大学地理空间信息学院，河南 郑州 450001

地图综合知识的抽象、获取和运用是实现地图综合自动化、智能化的关键[1]。利用程序语言翻译能够明确表达的综合约束是实现自动综合的经典思路[2]。但是，地图综合还受到制图经验、主观认知、视觉感受等诸多模糊因素[3]影响，综合知识难以全部清晰、准确形式化描述。机器学习技术能够从数据成果中发现模糊知识、辅助综合决策，推动了自动综合智能化升级[4]。化简作为重要综合算子之一[5]，基于机器学习的智能化简方法大体分为以下两类：①图形级方法。此类方法将构成图形的顶点作为基本处理单元，从顶点几何特征中抽象出与化简相关的特征项，智能算法通过学习、处理特征项实现压缩顶点的化简目的。文献[6—7]将顶点位置坐标作为特征项，分别利用遗传算法和蚁群模型处理特征项、优化顶点取舍，实现智能化简；文献[8]增加了夹角参数和垂线距离两个特征项，利用自组织神经网络聚类特征项实现顶点聚类和压缩；文献[9]提取了九个影响化简的顶点特征项，利用支持向量机对特征项进行监督学习实现智能化简。②图像级方法。此类方法以矢栅转换为基础、以图像像素为基本处理单元，利用智能算法从图像中学习化简算子。文献[10]利用三层BP神经网络从化简前后的栅格建筑物轮廓中学习、追踪化简轨迹实现化简处理；文献[11]利用卷积自编码器实现栅格建筑物模板匹配，并利用匹配模板化简建筑物轮廓。随着深度学习模型在图像翻译、风格迁移中成功应用[12-13]，学习、模拟从化简前到化简后图像变换的思路逐步展开。文献[4]利用U-net学习、模拟从化简前到化简后栅格建筑物轮廓变化；针对蜿蜒、绵长的线要素，文献[14—15]设计了专门的剖分及栅格样本生成方法，分别利用残差Unet、Pix2Pix等深度学习模型模拟从化简前到化简后的图像变换。

利用机器学习方法感知栅格图像、指导化简决策的学习模拟包含了对未被发现且难以形式化描述的模糊化简知识的利用，但受到矢栅转换损失的影响，以像素作为化简处理单元难以保证化简结果的点位准确。化简处理图形顶点能够保持化简结果点位准确，但仅利用可度量特征项学习模拟化简算子，局限于对已知明确化简知识的利用。本文基于集成学习策略[16]，通过集成几种机器学习算法，设计能够融合利用图形、图像学习模拟顶点取舍决策的智能化简方法，在确保点位准确的条件下，达到充分利用各种化简知识、优化智能化简效果的目的。

1 图形、图像融合利用的总体方案

集成学习通过构建、结合多个机器学习器完成学习任务[16]，以实现“博采众长”。融合利用图形、图像的集成学习化简方法的基本思路为：先分别构建基于图形和基于图像的顶点取舍模型，分别从图形特征层次和栅格图像层次对同一顶点的取舍情况进行学习和预测；再构建融合决策模型对基于图形和基于图像的顶点取舍进行融合利用，得到最终的取舍决策。总体方案如图1所示。

为方便后文叙述，将化简前、后的比例尺分别记为S1、S2，供模型训练的化简前、后的要素分别记为la、lb，模型应用中待化简要素记为lc。构成要素的顶点记为vi，la、lb和lc分别表示为la={vi|i∈[1,na]},lb={vi|i∈[1,nb]},lc={vi|i∈[1,nc]}。

2 基于图形的顶点取舍模型

2.1 基于图形的顶点取舍任务

图形是要素的矢量表达形式，适于空间量测、计算和分析。化简离不开对要素局部、整体形态特征的度量，图形几何特征的度量结果能够指导顶点取舍。本文采用18个图形特征项，从邻近顶点关系、弯曲结构和整体形态控制3个层次度量影响顶点取舍的几何特征。其中，基于邻近顶点的图形特征项包含对邻近顶点间距离、角度、垂距、弦长、弧长、面积、垂比弦和弧比弦的度量[9]，基于弯曲的图形特征项包含对左、右弯曲的基线长度、深度、面积和结构层次的度量[17]，基于整体形态控制的顶点特征项包含对顶点层次和形状控制程度的度量[18-19]。这些指标包含了对局部和整体形态特征的描述，涉及了影响邻近顶点取舍、弯曲取舍和整体形态控制点取舍因素的度量，体现了对顶点取舍已有知识的利用。

2.2 基于全连接神经网络的顶点取舍模型

全连接神经网络能够利用神经元间的连接关系融合利用多种特征，常用于基于特征项的智能决策[20]。全连接神经网络仅在相邻层神经元间构建连接关系，且每个神经元都与相邻层所有神经元连接。神经元连接参数为权重和偏置，图2(a)展示了基于权重和偏置的连接计算：xj为上一层神经元的输出值，y为下一层连接神经元的接收值；wj和b分别表示权重和偏置参数；f为激活函数，常采用非线性函数，以拟合复杂非线性任务。

面向基于图形的顶点取舍任务，设计基于全连接神经网络的顶点取舍模型构建从顶点图形特征项到顶点取舍的映射，如图2(b)所示。

图2 基于全连接神经网络的顶点取舍模型Fig.2 The model of vertex selection based on the fully connected neural network

(1)输入层含18个神经元，接收计算的18个顶点图形特征项FV1(vi),…,FV18(vi)。

(3)输入层和输出层之间可存在若干隐藏层，每个隐藏层内可包含若干神经元，能够利用顶点图形特征项生成多层次特征以指导顶点取舍。

2.3 模型参数的求解和优化

神经元间连接的权重和偏置参数是影响模型计算准确性的关键，利用基于图形特征的顶点取舍样本训练模型，自适应求解、优化模型参数，使其适用于基于图形的顶点取舍任务。

构建基于图形特征的顶点取舍样本集。采用三元法记录基于图形特征的顶点取舍样本，即〈顶点，顶点图形特征，取舍情况〉。对于顶点vi，计算图形特征项，记为FV(vi)={FV1(vi),…,FV18(vi)}；采用独热(One-Hot)编码[21]标记顶点取舍情况，记为[ti1,ti2]∈{[1,0],[0,1]}，其中[1,0]表示vi被保留，[0,1]表示vi被删除。对于训练数据la、lb，化简前线要素la各顶点的取舍情况可以通过与化简后线要素lb的匹配关系判定，具体方法参照文献[9]。遍历la各顶点，得到训练样本集{〈vi,FV(vi),[ti1,ti2]〉|i∈[1,na]}。

3 基于图像的顶点取舍模型

3.1 基于图像的顶点取舍任务

图像是要素的栅格表达形式，常作为机器视觉的感知对象。除明确可度量的图形特征外，影响顶点取舍的因素还隐含于制图员对包含顶点上下文环境的主观感受及其引发的难以形式化描述的知识中。在视觉分辨率约束下提取包含顶点在内一定区域的栅格图像，可以看作是人眼感受到的顶点上下文环境；利用机器学习方法从栅格图像中感知顶点取舍是对人眼感受顶点上下文环境指导顶点取舍的模拟，涵盖了对潜在影响顶点取舍模糊知识的利用。

指导顶点取舍判断的栅格图像应满足：①图像像素对应的实际距离小于原始比例尺图上最小可视距离[22]对应的实际距离，保证栅格图像中要素细节足够清晰。即满足pixsvo/S2，其中npix为图像行(列)像素个数。基于①、②，设计对vi提取栅格图像的方法，记为FI(vi)，具体如下。

(1)构建包含vi的待化简要素的外接矩形。

(2)以vi为中心，构建与外接矩形各边平行且边长为pix·npix的正方形区域。

(3)利用矢栅转化方法[23]将包含于正方形区域内的矢量要素转换为栅格图像，像素大小为pix，图像尺寸为npix·npix。

3.2 基于卷积神经网络的顶点取舍模型

卷积神经网络能够利用卷积核和局部感受野从图像中感知多层次特征，常用于基于图像的智能决策[24-26]。卷积是感知栅格图像特征的关键,图像卷积计算方法详见文献[24]。输入图像与卷积核进行卷积运算生成特征图，特征图中的特征值是卷积核对局部感受野感知的结果，如图3(a)中输入图像红框区域对应特征图红框区域的局部感受野；卷积核规模和步长影响局部感受野的范围和位置，卷积核的权重影响局部感受野的感受结果；具有不同权重、不同规模、不同步长的卷积核能够对局部感受野进行多样感知，得到不同特征图，如图3(a)中不同权重、不同步长的卷积运算产生了不同的特征图；特征图再次进行卷积运算，可以提取更深层次的特征图、获取多层次感知。此外，池化运算[24-25]能够对一定范围内的特征值进行下采样，实现特征图压缩，得到更加概略的感知结果，如图3(b)所示。卷积神经网络通过重复布设卷积层和池化层提取、利用多层次特征，如图3(c)所示。卷积层和池化层的计算过程分别表示为Y=f(Conv(X,WJ)+BJ)和Y=Sub(X)，X和Y分别为卷积层(或池化层)的输入和输出像素值(或特征值)矩阵；f为激活函数；WJ为卷积核权重矩阵；BJ为偏置参数。

图3 利用卷积、池化感知图像多层次特征Fig.3 Extraction of multi-level features using convolution and pooling

面向基于图像的顶点取舍任务，设计基于卷积神经网络的顶点取舍模型构建从栅格图像到顶点取舍的映射，如图4(a)所示。

图4 基于卷积神经网络的顶点取舍模型Fig.4 The model of vertex selection based on the convolutional neural network

(1)输入层接收栅格图像FI(vi)的像素值矩阵。

(3)隐藏层由一个独立卷积层、多个残差块和一个全连接层构成：卷积层用于从输入图像中提取与顶点取舍相关的特征图；残差块用于进一步提取更深层次的特征图，并通过跳跃连接融合利用不同层次的特征图；全连接层利用最后一个残差块生成的特征图的特征值计算顶点取舍情况。其中，卷积层和残差块的结构如图4(b)所示：卷积层中引入批量标准化(batch normalization，BN)[27]以缓解梯度消失的问题[28]，且引入批量标准化还能约减卷积层偏置参数[28]，使计算过程简化为Y=f(BN(Conv(X,WJ)))；残差块可以看作由两个具有跳跃连接的卷积层构成，能够避免神经网络深度增加引发的退化问题[29]，残差块计算见式(1)、式(2)

Y=f(Sub(X)+BN(Conv(f(BN(Conv(X,WJ)))),WJ+1))

(1)

Y=f(X+BN(Conv(f(BN(Conv(X,WJ)))),WJ+1))

(2)

式(1)、式(2)分别表示残差块是、否对特征图尺寸进行压缩，式(1)通过调整卷积步长压缩特征图使其与Sub(X)尺寸相同。

3.3 模型参数的求解和优化

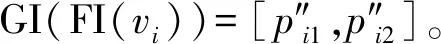
4 图形-图像融合决策模型

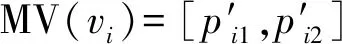
(3)

4.1 线性加权融合模型

线性加权法是实现多指标融合的常用方法[30]，MV和MI的输出结果通过线性加权模型实现融合利用，如式(4)所示

(4)

顶点取舍模型越准确，预测的取舍结果越可靠，融合时所占权重越大。因此，MV和MI的权重(即λ′和λ″，且λ′+λ″=1)由两模型精度计算而得，如式(5)所示

(5)

式中，Eva是对模型精度的评价，详见式(6)

(6)

可采用查准率(Precision)、查全率(Recall)、准确率(Accuracy)和F1度量(F1score)等指标评价法。具体而言，就是利用MV(或MI)对训练样本集进行测试，将预测的顶点取舍情况与实际取舍情况进行比较，计算查准率、查全率、准确率和F1度量(计算方法参见文献[31])评价模型精度。

4.2 贝叶斯融合模型

MV和MI模型的输出结果都是顶点取舍概率，基于此，可计算在已知基于图形和基于图像的顶点取舍概率情况下的顶点取舍条件概率，即计算P([ti1,ti2]|MV(vi),MI(vi))。利用朴素贝叶斯方法，对P([ti1,ti2]|MV(vi),MI(vi))进行分解、转化，如式(7)

(7)

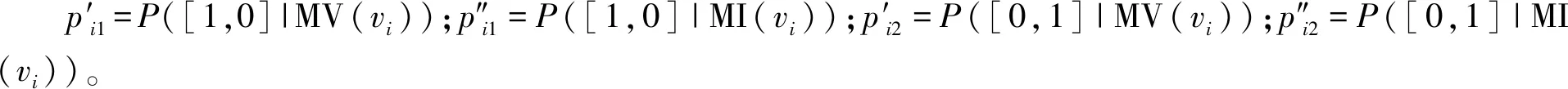
(8)

(9)

4.3 支持向量机融合模型

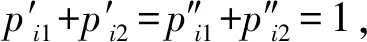
(10)

(11)

式中，C为惩罚系数；ξ(i)为松弛因子，利用此目标函数能够实现软分类。

软分类使大部分支持向量被正确分类，适用于处理由MV和MI生成的不完全准确的支持向量。将求解的超平面参数μ和η应用于式(12)，完成SVM二分类器构建

(12)

4.4 人工神经网络融合模型

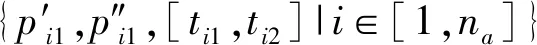
(13)

5 试验用例：化简岛屿岸线

5.1 方法有效性验证

岛屿岸线形态复杂多变，是化简难度最大的要素之一[32]，以新西兰Stewart岛屿岸线作为试验对象验证各模型有效性。1∶5万Stewart岛屿岸线包含20 775个顶点，其中前19 104个顶点用于训练，最后1761个顶点用于测试，如图5(a)所示；采用文献[9]中顶点取舍案例获取方法，从人工综合的1∶25万Stewart岛屿岸线数据中提取顶点取舍结果作为标准化简结果，如图5(b)所示。基于TensorFlow框架，利用Python语言在GPU RTX 2070s的运算环境下实现本文方法，学习、模拟从1∶5万至1∶25万的顶点取舍决策。

图5 试验数据Fig.5 Experimental data

分别从训练部分和测试部分中提取样本并构建训练集和测试集。提取栅格图像时，令svo=0.2 mm,pix=svo/2S1=5 m,npix=128；且考虑到文献[15]指出面状图斑比栅格曲线更容易被卷积神经网络学习，从岛屿面域中提取包含顶点上下文环境的栅格图像如图6所示。

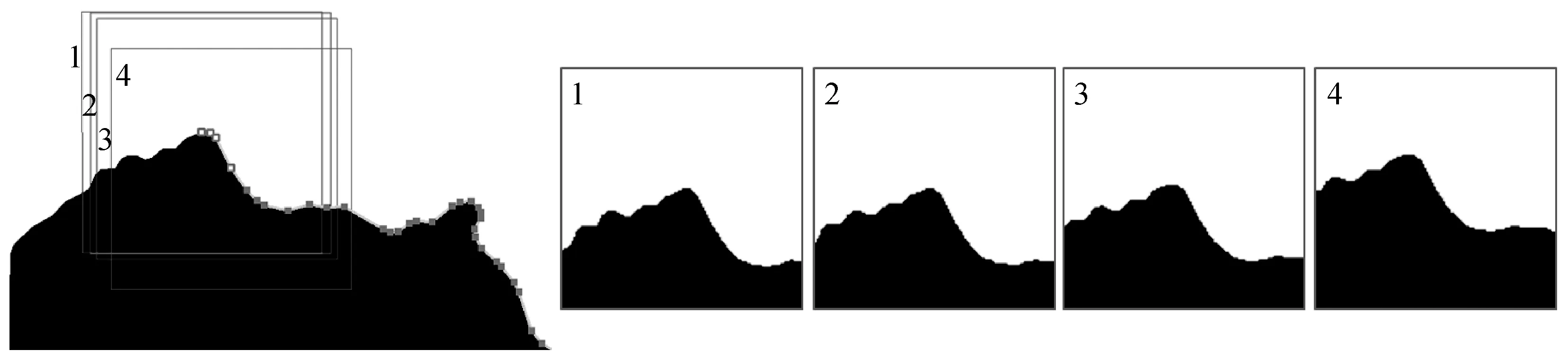
图6 提取栅格图像的示例Fig.6 Examples of extracting raster samples

构建、训练全连接神经网络和卷积神经网络，实现基于图形和图像的顶点取舍。其中，全连接神经网络2个隐藏层的神经元数依次为64和32；卷积神经网络包含1个卷积层、4个残差块和1个全连接层，卷积核大小依次为3×3、8×8、6×6、3×3、3×3，残差块将特征图大小依次压缩为1/4、1/4、1/2、1/2。试验所有神经网络中间层激活函数均为ReLU函数[20]，损失函数均为交叉熵函数[20]，梯度下降方法均采用Adam方法[33]。全连接神经网络和卷积神经网络训练终止条件分别为ne=20和ne=50，训练过程中对训练集拟合准确率变化如图7所示。基于训练集和测试集数据评价训练后的MV和MI，统计查准率、查全率、准确率和F1度量，见表1。由图7和表1可知，MV和MI分别一定程度上学习、掌握了岸线化简中的顶点取舍，都具有一定泛化应用能力，且MV优于MI。

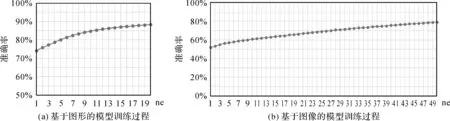
图7 基于图形和基于图像的顶点取舍模型训练过程中训练集准确率的变化Fig.7 The accuracy changes with training of vector-based and raster-based models

表1 利用训练集和测试集对MV和MI的效果评价Tab.1 Assessments of MV and MI based on training and testing data (%)

构建以下几个融合决策模型：①分别基于训练集Precision、Recall、Accuracy和F1score构建4个加权融合模型，分别记为PreFu、RecFu、AccFu和F1Fu；②构建一个贝叶斯融合模型，记为BayFu；③构建一个采用高斯核函数、惩罚系数为0.01的支持向量机融合模型，记为SVMFu；④构建一个隐藏层包含32个神经元的全连接神经网络，由该神经网络对训练集数据重复学习10次训练而得的融合模型记为NNFu。利用融合模型处理训练集和测试集，计算查准率、查全率、准确率和F1度量评价顶点取舍效果，如表2所示。由于F1score是对Precision和Recall的加权平均，着重基于Accuracy和F1score分析各融合模型效果。

(1)所有融合模型都实现了对图形决策和图像决策的集成，使融合前效果相对较差的模型得到显著提升。表2中所有融合模型的Accuracy和F1score值高于表1中融合前MI模型的Accuracy和F1score值，融合模型使MI精度得到提升。但是，融合模型的Accuracy和F1score值不都高于融合前的MV模型，部分融合模型使MV精度受损。

表2 利用训练集和测试集对融合模型效果的评价Tab.2 Assessments of fusion models based on training and testing data (%)

(2)RecFu、AccFu、F1Fu和BayFu没有起到融合利用MV和MI结果、提升顶点取舍精度的效果。对于训练集，RecFu、AccFu、F1Fu和BayFu的Accuracy和F1score值低于MV。这些模型属于加权融合模型或贝叶斯融合模型，是在一定假设基础上构建的融合模型。其中，加权融合模型假设MV与MI输出结果间存在线性关系，贝叶斯融合模型中假设概率可以被频率近似。这些固定假设影响了模型应用的灵活性和适应性，导致融合效果不佳、准确率损失等问题。

(3)PreFu、SVMFu和NNFu起到了提升顶点取舍精度的效果，实现了图形和图像决策的融合利用。对于训练集和测试集，PreFu、SVMFu和NNFu的Accuracy和F1score值高于MV和MI。这些融合模型大都以机器学习为基础，支持向量机和人工神经网络能够从融合数据集中发现规律、指导融合应用，用于关系脆弱且不明确的MV和MI结果数据融合时，具有更好的灵活性和适应性。

对PreFu、SVMFu和NNFu的化简效果展开进一步分析。

(1)从顶点取舍的准确性看，无论是基于训练集还是测试集，表2中NNFu的Accuracy和F1score值都高于PreFu和SVMFu，神经网络更好的灵活性和适应性使NNFu的顶点取舍精度高于SVMFu和PreFu。

(2)从化简结果的视觉感受上看，PreFu、SVMFu和NNFu都能融合利用MV和MI，在一定程度上起到了优势互补的效果。部分测试弧段的化简效果如图8所示：对于区域1内的弧段，MV的化简结果与目标化简结果更加一致；对于区域2内的弧段，MI的化简结果与目标化简结果更加一致；NNFu化简区域1的结果与MV相似，化简区域2的结果与MI相似，体现了对MI和MV融合利用和优势互补；SVMFu化简区域2的结果与MI相似，化简区域1的结果略逊于MV的化简结果、但明显优于MI的化简结果，在一定程度上体现了对MV和MI的融合利用；PreFu化简区域1和区域2的结果与MV相似，仅使区域1和区域2间弧段的化简效果得到改善，表现出对MV的严重依赖和对MI的利用不足。

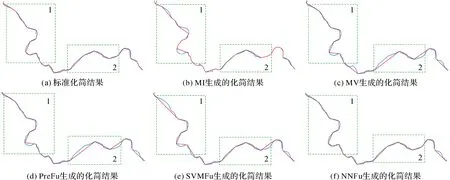
图8 部分测试弧段的化简结果(蓝色和红色曲线分别表示原始岸线和化简结果)Fig.8 Simplified results of part of test data with different models (the original coastlines and simplified coastlines are colored by bule and red respectively)

(3)计算Hausdorff距离[34]、面积差[35]、符号重叠率[36]、视觉缓冲区限差[15,34]度量模型化简结果与标准化简结果间的相似性(表3)，量化评价各模型的整体化简效果。其中，Hausdorff距离、面积差越小，模型化简结果与标准化简结果越相似；符号重叠率、视觉缓冲区限差越大，模型化简结果与标准结果越相似，符号重叠率的线宽设置为0.1 mm，视觉缓冲区限差的最小可分辨距离设置为0.2 mm。从符号重叠率上看，PreFu和MV相差不大，但从Hausdorff距离、面积差和视觉缓冲区限差上看，PreFu生成的化简结果没有比MV更接近于标准化简结果，融合效果并不理想；从所有指标上看，SVMFu和NNFu生成的化简结果与标准化简结果的相似性都高于MV和MI，融合效果良好；且NNFu的化简结果与标准化简结果具有最高的相似性，做到了相对最优的融合利用。

表3 测试弧段化简结果与标准化简结果的相似性评价Tab.3 Evaluation of similarities between automated results and target results for the testing data

类似地，利用本文方法进行多尺度化简试验，并计算测试部分海岸线由1∶5万化简至1∶25万、1∶50万、1∶75万和1∶100万时线要素化简前后的顶点压缩率[9]、长度比[15]、Hausdorff距离、面积差和平均曲率相似度[37]，见表4。本文方法能够进行多尺度化简，且比例尺跨度越大、化简结果越概略，符合多尺度变化的客观规律；各尺度化简结果与原始线要素的曲折程度一致性较高，保持了良好的几何相似性。

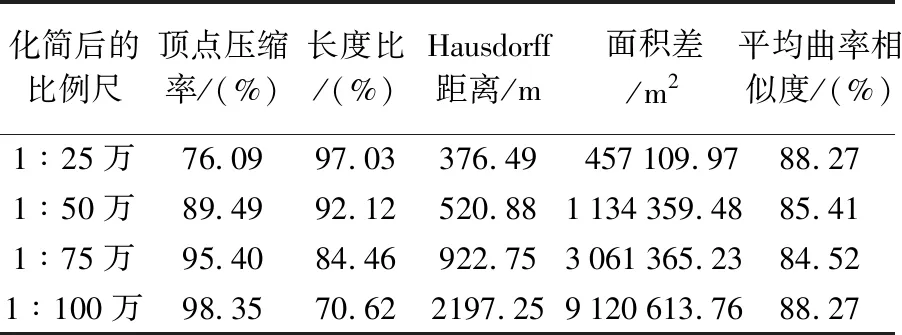
表4 测试部分海岸线多尺度化简结果的评价Tab.4 Evaluations of multi-scale simplifications of the testing coastline

5.2 方法优越性验证

令融合效果最好的NNFu模型与以下化简方法进行对比，验证本文方法的优越性。

5.2.1 与其他智能化简方法的对比分析。

文献[9]是近些年具有代表性的智能化简方法，但其采用的特征项不及本文采用的18种顶点特征项丰富、全面。为增强两方法的可比性、控制对比试验变量，对比方法1采用文献[9]方法并将其特征项扩展至与本方法相同。利用训练部分岸线对方法1进行训练，过程如图9所示，迭代至5500次时方法1的准确率和F1度量都相对较高，利用此时的模型对测试部分进行化简，化简结果的量化评估如表5所示。

图9 方法1在训练过程中模型准确率和F1 score的变化Fig.9 The accuracy and F1 score changes with training of the comparison method 1

比较表1—3与表5发现：方法1对训练集的学习效果和测试集的预测效果都没有达到NNFu模型的效果，甚至逊于融合前的MV模型。这是因为方法1采用的支持向量机模型的学习能力通常被认为弱于MV模型采用的多层全连接神经网络，其难以充分学习掌握岸线顶点取舍这一相对复杂任务；此外，方法1只顾及了可度量的图形特征，而NNFu模型还融合了隐含于图像中的模糊知识。综上所述，本文方法优于方法1。

表5 方法1对测试部分海岸线化简效果的评价Tab.5 Evaluation of the contrast method simplification for the testing data

5.2.2 与其他自动化简方法的对比分析。

文献[32，35，38—39]是近些年具有代表性的自动化简方法。其中，文献[35，39]是基于顶点的化简方法，文献[32，38]是基于弯曲的化简方法，都可用于岸线化简。文献[35，39]方法记为方法2和方法3，都参照文献[35]控制两方法的化简参数，使化简结果与标准化简结果的顶点数相同；文献[38]记为方法4，弯曲化简的宽度阈值和深度阈值设置为0.3 mm和0.5 mm；文献[32]记为方法5。利用方法2—5化简测试部分岸线，化简结果量化评价如表6所示。

表6 方法2—5化简结果与标准化简结果的相似性评价Tab.6 Evaluation of similarities between automated results of contrast methods 2—5 and target results

分析表6与表3可以发现：方法2顾及了化简前后的面积保持，面积差、符号重叠率、视觉缓冲区限差都优于方法3—方法5，与标准化简结果具有很好的整体相似性，但除视觉缓冲区限差外，面积差、符号重叠率都没有达到NNFu的水平，且严格保证化简前后面积相等会导致局部变形较大，表现为Hausdorff距离相对最大；方法3化简结果与标准化简结果的整体相似性逊于NNFu，但方法3在压缩顶点的同时允许在可视范围内移动顶点，使表征局部相似性的Hausdorff距离优于NNFu；方法4—5化简结果与标准化简结果的整体相似更差，这是由于弯曲比顶点的处理粒度更粗，容易产生更大的变形；特别是方法5面向海图应用，以单侧弯曲化简为主，与标准化简结果的整体相似最弱。这些自动化简方法往往只顾及有限约束，且只在约束范围内效果良好，表现为方法2—5化简结果的量化评价中可能存在1个指标优于NNFu的化简结果；而实际地图综合中化简约束往往是多元混合的，本文方法从数据成果中学习化简决策，更具优越性和适应性，表现为方法2—5优于NNFu的量化评价指标最多不超过1个。

进一步验证本文方法的优越性与适应性，扩充测试数据并与具有广泛适用性的化简方法3、4进行对比试验：利用NNFu化简新西兰南岛的4段岸线(表7)，计算化简后的顶点压缩率[9]、弯曲压缩率[38]；利用方法3化简岸线1—4至与NNFu相同的顶点压缩率，各化简结果的位置误差[40]如表8所示；利用方法4重复删除细小弯曲，直至化简后岸线1—4的弯曲压缩率恰好不大于NNFu化简结果为止，各化简结果的位置误差见表9。

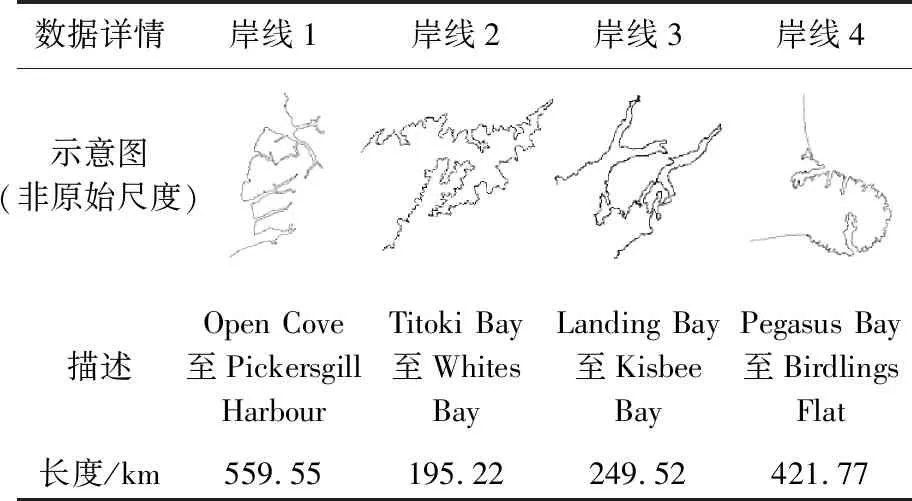
表7 其他1∶5万的海岸线数据Tab.7 Some other coastlines to be simplified

分析表8、表9可知：在相同的顶点压缩率下，NNFu化简岸线1—4的位置误差比方法3更小；在相似的弯曲压缩率下，本文方法较方法4能够压缩更多的弯曲且产生更小的位置误差，本文方法更好地保持了化简前后的整体相似性。此外，在保持不同海岸地理特征上，本文方法也具有一定优势。图10(a)中，本文方法更好地保持了人工岸线规则平直的特征，方法3、4对其中海岸人工建筑[41](虚线框内)的不良化简破坏了其原本地理意义；图10(b)中，本文方法更好地保持了海湾的整体形态及湾口位置的准确性(虚线框内)，确保了对化简前、后海湾地理特征认识的一致性；图10(c)中，本文方法较方法4更好地化简了狭长河口(虚线框内)，较方法3更好地保持了曲折部分与平滑部分的差异性。综上所述，进一步证实了本文方法的优越性和适应性。

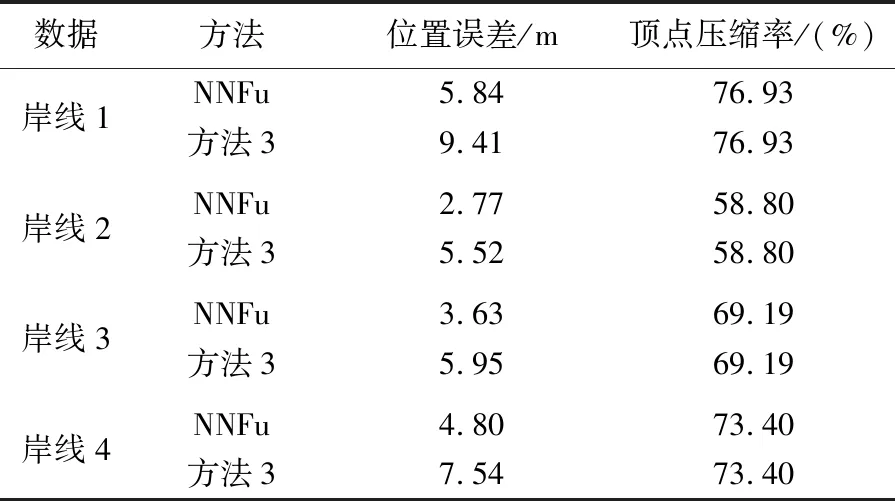
表8 方法3和NNFu化简效果的比较Tab.8 Comparisons on different simplifications with same vertex compression ratio

表9 方法4和NNFu化简效果的比较Tab.9 Comparisons on different simplifications with similar bend compression ratio

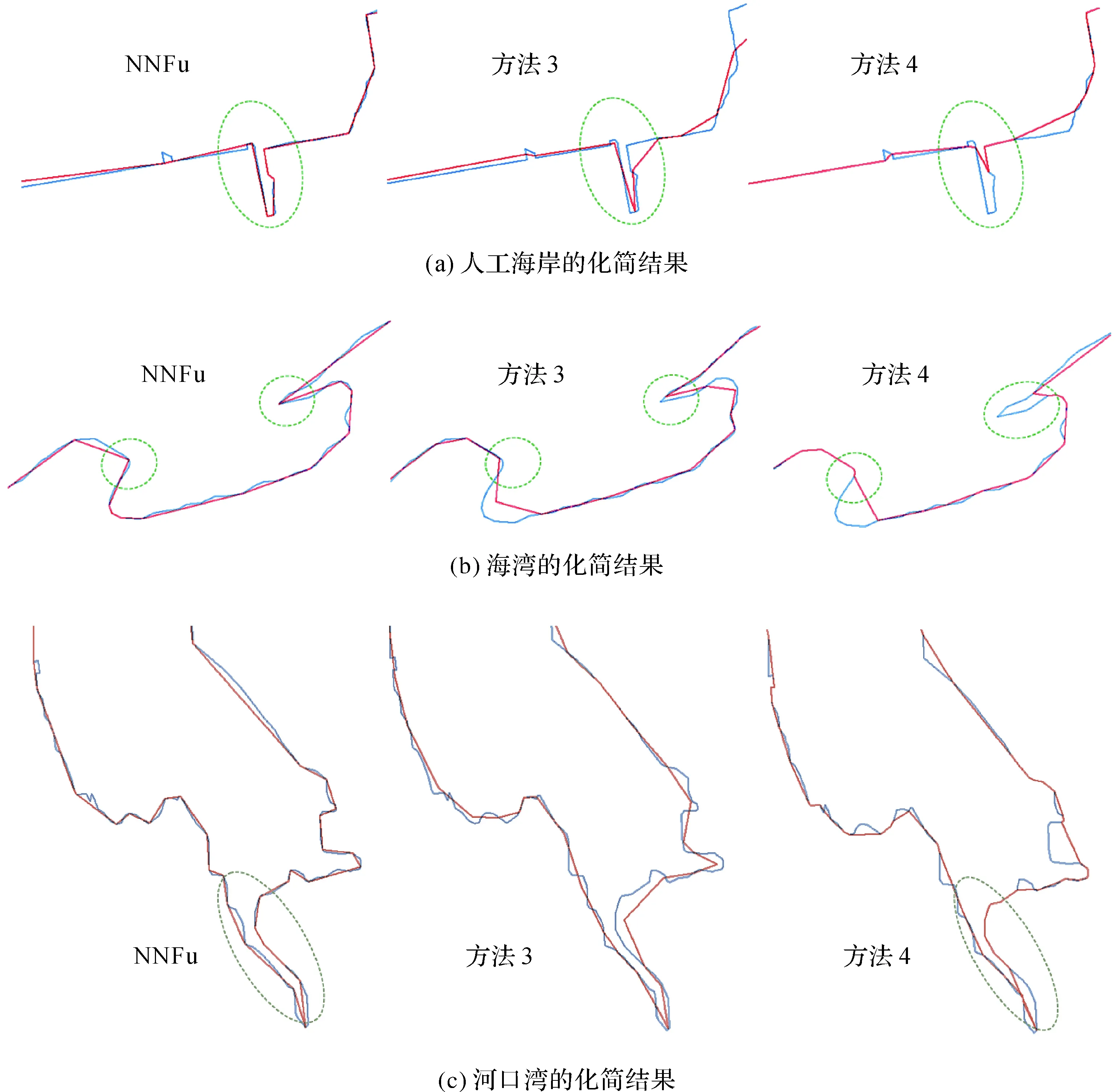
图10 不同类型海岸线化简效果的比较(蓝色曲线为原始岸线、红色曲线为化简结果)Fig.10 Comparison of different simplifications of various coasts:the original coastlines and simplified coastlines are colored by bule and red respectively

6 结 论

本文集成几种机器学习算法学习、模拟、优化化简过程中的顶点取舍决策：利用全连接神经网络构建了基于图形的顶点取舍模型，利用卷积神经网络构建了基于图像的顶点取舍模型，利用线性加权、贝叶斯理论、支持向量机、全连接神经网络建立了能够综合利用基于图形和基于图像的顶点取舍的诸多融合决策模型，实现了融合利用图形和图像中蕴含的化简知识学习模拟顶点取舍的智能化简，起到了顶点取舍优化、化简精度提高、不同模型优势互补的良好效果。

在实际应用中，不是所有融合决策模型都发挥了良好效果，如何选择、衡量、解释融合决策模型还需进一步研究；此外，向智能化简模型中引入明确的地图综合知识以增强智能方法可解释性和约束性，也是十分重要研究。特别的，本文提出的图形、图像融合利用的思路还能用于指导模式识别、数据增强和其他综合算子中智能方法(如文献[4,25—26,42])的优化升级。沿着多特征融合利用的集成学习思路，融合语义特征、三维特征等更加丰富的特征项，集成图卷积神经网络[42]、生成对抗网络[15]等更加多元的机器学习算法，都值得进一步探索。