GNSS水汽层析的自适应非均匀指数分层方法

王 昊，丁 楠，张文渊，冯遵德，赵长胜，闫香蓉

1.江苏师范大学地理测绘与城乡规划学院，江苏 徐州 221116；2.中国矿业大学环境与测绘学院，江苏 徐州 221116

大气水汽是影响气候变化的关键气象要素，对大气能量输送和对流天气的演变具有重要影响作用[1-2]。传统水汽探测手段，如无线电探空技术、水汽微波辐射计等，由于具有诸多局限性，已不能满足目前实时、快捷、精确地获取水汽要素的要求。随着GNSS技术在气象学中的应用发展，利用GNSS技术进行对流层三维水汽场的反演已快速成为一种新兴水汽探测手段。GNSS水汽层析技术具有精确、快速、全天候和低成本等诸多优势[3]，已在大气水汽监测中得到越来越多的应用。

文献[4]率先发展了GNSS水汽层析技术，研究了垂直分层对水汽层析结果精度的影响规律，基于夏威夷Kilauea GPS网进行了水汽层析试验，通过对比欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts，ECMWF)的数据，得出了垂直分层的最小分辨率需大于300 m以削弱噪声影响并保证层析结果精度的结论。垂直分层是GNSS水汽层析的关键技术之一，基于文献[4]的水汽层析思路，诸多学者对这一关键技术进行了研究，目前主要分为两类：一类为采用恒定高度间隔的均匀分层；另一类为采用不同高度间隔的非均匀分层。在均匀分层的研究中，文献[5]采用3种不同高度间隔(600、800、1000 m)的等距均匀垂直分层进行层析试验，发现采用均匀分层时以800 m为间隔最优。在非均匀分层的研究中，文献[6]以四川省为例对非均匀分层与均匀分层进行对比试验，研究并分析了采用非均匀分层对层析结果的影响。文献[7]基于探空数据研究了层析区域的顶层边界高度，提出了两种不同非均匀分层模型，并对比了两种模型的卫星信号利用率和体素块利用率。文献[8]提出了一种体素块优化的层析区域建模思路，在垂直方向上以1973—2012年探空水汽廓线为依据对香港地区进行4种不同的垂直分层建模，对比分析了不同高度间隔的非均匀分层模型对层析结果质量的影响。

传统的垂直分层建模方法将研究区域按等高度间距于垂直方向进行划分[9]，该方法属于均匀分层，优势在于操作简便且分层后获得的离散区域形状规则[10]。由于大气水汽在垂直方向上呈指数递减趋势，因此建模时采用均匀分层的不足之处在于均匀的垂直分辨率不符合大气水汽的实际分布，会引入一定的误差。而非均匀分层模型的垂直分辨率更加符合大气水汽的实际分布，采用非均匀分层模型进行离散化能有效减小上述误差。为削弱垂直分层建模过程中误差的影响，非均匀分层模型已被广泛运用于GNSS水汽层析技术之中[11-12]，但目前非均匀分层的建模方法仍然存在不足，非均匀分层模型的垂直分辨率设置尚未形成科学可靠且适用性强的参考标准，部分层析试验在采用非均匀分层模型时仅根据固定的经验设置上疏下密的分层高度区间，并无科学可靠的分层依据[13]；另一部分试验虽基于先验水汽密度进行建模，但仍存在分层模型适用性不高的问题，在层析区域变更或大气水汽垂直分布特征发生变化的情况下无法实现方便快捷的自适应分层[7-8,14]。

针对上述问题，本文提出一种自适应非均匀指数分层(adaptive non-uniform exponential vertical stratification，ANEVS)的GNSS水汽层析方法，详细阐述了该垂直分层方法的分层步骤和具体公式。该方法基于层析区域内大气水汽于垂直方向上呈指数递减的分布特征，能够自适应地完成任意给定层析区域的非均匀垂直分层建模，优化各层水汽密度参数的分配，缩小底层各层水汽密度参数之间的差异，提高了垂直分层的合理性和真实性，进而改善层析结果质量，提高层析解算精度，同时弥补了垂直分层模型适用性低的问题。

1 GNSS水汽层析基本原理

GNSS水汽层析技术将连续的研究区域离散化为数量有限的体素块，以卫星信号的斜路径湿延迟(slant wet delay，SWD)为观测值构建大气水汽参数、信号传播距离与信号传播路径上的总水汽含量[15]之间的函数关系，反演出水汽的三维空间分布信息[16]。

GNSS水汽层析以每条信号的SWD为观测值。忽略信号传播过程中的弯曲量，假设传播路径为三维空间直线，同时假设各体素块内水汽密度在一个层析历元内为常数。在此基础上建立模型为

(1)

式中，SWDi表示第i条卫星信号的斜路径湿延迟；lij表示第i条信号穿过第j个体素块的直线长度；Dj表示第j个体素块内的水汽参数，这里为该体素块的待求水汽密度；n表示总体素块个数。

基于上述模型构建的观测方程组系数矩阵严重秩亏，因此在构建层析方程组时，一般通过加入约束条件以解决层析方程组的不适定性问题[17-18]。约束条件主要包括垂直约束、水平约束和顶层约束。垂直约束采用指数函数进行约束，其模型为[19]

(2)

式中，hi和hj分别表示大气高度；ρi和ρj分别表示高度hi和hj处的水汽密度；H表示水汽标高[20]。

水平约束采用高斯加权函数进行约束，其模型为[21]

w1D1+w2D2+…+wi-1Di-1+wi+1Di+1+

+wjDj=Di

(3)

(4)

式中，Di表示同层第i个体素块内的水汽密度；wi表示同层第i个水汽密度的权系数；dij表示第i个体素块与同层第j个体素块中点之间的距离；σ表示平滑因子[22]，其取值与体素块水平方向的长度有关[21]，本文的平滑因子取值为15。

顶层约束将最顶层体素块内的水汽密度按照经验强制约束为某一定值，部分层析试验将顶层水汽密度值约束为0.01 g/m3[23]，但顶层体素块实际具有一定高度，仅顶层体素块顶端水汽密度值接近0.01 g/m3，中间及底端水汽密度大于0.01 g/m3，因此本文以先验探空数据为依据，采用顶层体素块高度区间内的探空水汽密度均值为约束值。

结合观测方程和约束条件的层析方程组可以表示为

(5)

式中，A0、AV、AH、AT分别表示观测值系数矩阵、垂直约束系数矩阵、水平约束系数矩阵、顶层约束系数矩阵；DW表示待求水汽密度向量；b0、bV、bH、bT分别表示对应的观测值向量，其中，bV、bH一般情况下为0向量；方程总个数m等于各部分方程个数o、t、v、h之和。

式(5)的解算方法有奇异值分解法、最小二乘法、代数重构法(algebraic reconstruction technique，ART)等[24-25]，本文采用ART对层析方程组进行解算。ART避免了系数矩阵的求逆运算，具有抗噪性强的优点，即使在观测方程较少、信号分布不均匀和信号噪声较大的不利条件下，也能解算出精度较高的结果[26-27]。

2 基于水汽垂直分布特征的自适应非均匀指数分层方法

自适应非均匀指数分层方法总体分为两大步骤：首先，对层析区域进行大气水汽的垂直分布建模，以该区域的先验水汽廓线信息为依据获得大气水汽的垂直分布特征函数；然后，基于该水汽垂直分布特征函数，通过迭代的方式进行各层高度区间的计算，实现对任意层析区域进行任意层数划分的自适应分层。

2.1 水汽垂直分布建模

非均匀指数分层基于先验水汽垂直分布特征函数，以水汽密度区间计算分层高度区间，在进行自适应分层前需先对层析区域大气水汽的垂直分布进行建模，以获取高度与水汽密度之间的函数关系。

基于水汽密度随高度增加呈指数递减规律对大气水汽的垂直分布特征进行建模[28]，高度h处的水汽密度表达为

(6)

式中，ρh表示高度h处的水汽密度，单位为g/m3；ρ0表示地表处水汽密度参数；Dv表示水汽垂直分布特征参数；H表示水汽标高，单位为m[20]。

由式(6)可知，某一高度h处的水汽密度值ρh(g/m3)可表示为高度h的函数，其中包含水汽密度参数ρ0和水汽垂直分布特征参数Dv两个未知参数，通过对研究区域的先验水汽密度数据进行拟合可获得式(6)中的两个未知参数。获得先验水汽密度数据的方法有多种，以探空气象站的探空数据为例，探空数据具有高垂直分辨率的优点，高精度的先验探空水汽密度可通过原始探空资料中包含的温度、露点温度等观测数据进行计算，水汽密度Dw计算公式为

(7)

式中，e表示水汽分压，单位为hPa；Rv=461.5 J·kg-1·K-1；T表示温度，单位为K。其中，e可由世界气象组织推荐的Goff-Gratch公式计算

(8)

式中，T1=273.16 K；Td表示露点温度，单位为K；e表示水汽分压，单位为hPa。

上述部分详细阐述了利用探空数据计算先验水汽密度的公式和步骤，但由于探空数据的空间分辨率和时间分辨率较低，可能出现层析区域或层析时间段内探空数据无法获取的情况。针对该情况，利用ECMWF或美国国家环境预报中心(European Centre for Medium-Range Weather Forecasts，NCEP)提供的再分析资料中温度和相对湿度等气象数据同样可以获得可靠的先验水汽密度数据[18,29]。

图1为水汽垂直分布特征拟合图，其中散点代表每一高度位置处所对应的实测探空水汽密度，曲线代表最小二乘拟合后的函数曲线，设拟合后曲线的函数表达式为

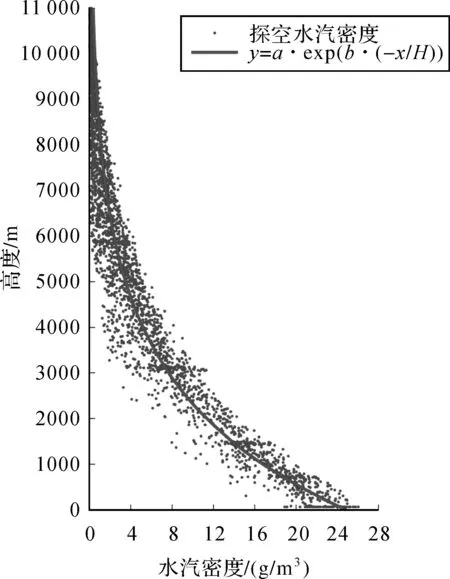
图1 水汽垂直分布特征拟合Fig.1 Vertical distribution characteristics of water vapor

(9)

式中，x表示高度，单位为m；y表示水汽密度，单位为g/m3；a和b分别表示地表处水汽密度参数ρ0和水汽垂直分布特征参数Dv拟合后的具体数值；H表示水汽标高，单位为m。式(9)反映了层析区域内大气水汽于垂直方向上的总体分布特征，为下一步自适应分层提供了高度值与水汽密度值之间的具体函数关系。

2.2 自适应非均匀指数分层

在获得如式(9)所示的层析区域水汽垂直分布特征函数后，可通过如下方法进行自适应垂直分层：将层析区域划分为L层，基于文献[4]的研究，垂直分层间隔需大于300 m[4]，首先将第1层高度区间设置为[0,300]，根据式(9)计算300 m处水汽密度为a·eb·(-300/H)(g/m3)，第1层水汽密度区间为[a,a·eb·(-300/H)]，现还需将剩余高度划分为L-1个高度区间，计算剩余L-1层每层水汽密度间隔为(a·eb·(-300/H)-0.1)/(L-1)，单位为m，以该值计算各层预设水汽密度区间，得剩余L-1层的预设水汽密度区间表达式为

(10)

式中，a、b、H表示含义与式(9)相同；n表示层数(2≤n≤L)；L表示预计划分总层次数。

将剩余L-1层对应式(10)的预设水汽密度区间代入式(9)，反推计算出剩余L-1层的预设高度区间，其中第2层预设高度区间为

(11)

式中，a、b、H、L表示含义与式(10)相同。

若该层高度间隔大于300 m，则以此时的预设高度区间为结果，完成非均匀指数分层；若该层高度间隔小于300 m，则将该层高度区间继续以最小高度间隔300 m设置为1层，例如第2层高度区间为[300,600]，密度区间为[a·eb·(-300/H),a·eb·(-600/H)]，剩余层数为L-2，每层密度间隔为(a·eb·(-600/H)-0.1)/(L-2)，以新的密度间隔计算新的剩余层预设密度区间，在进行第m次以300 m为高度间隔划分最底层后，剩余层的预设密度区间可表示为

(12)

式中，a、b、H表示含义与式(11)相同；m表示以300 m为高度间隔进行划分的层次数量；n表示剩余第m+1层至L层的层号(m+1≤n≤L)；L表示预计划分总层次数。

每次迭代，将式(12)的剩余层预设密度区间代入式(9)反推新的预设高度区间，判断其中最低层高度间隔是否大于300 m，最低层高度间隔表示为

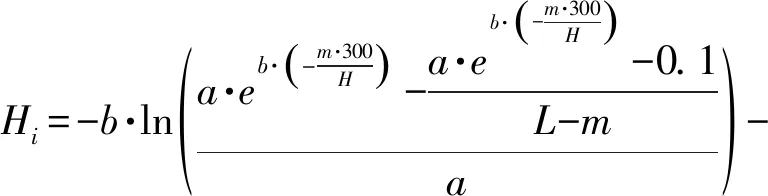
(13)

式中，a、b、H、m、L含义与式(12)相同；Hi表示剩余L-m层中最底层高度间隔，单位为m，若Hi大于300 m则完成非均匀指数分层，反之则继续以300 m为高度间隔划分剩余L-m层中的最底层并以此类推。

上述的自适应非均匀指数分层如图2所示。ANEVS进行垂直分层时，先通过所需分层层数计算水汽密度区间，再通过水汽密度区间和先验水汽垂直分布特征函数反推高度区间，通过迭代判断并调整最底层高度间隔。该方法能根据层析区域的大气水汽垂直分布特征和所需分层层数自动调整分层高度区间，同时自适应地控制各层水汽密度差异在一个很小的范围内，做到细分底层区域密度不同的水汽、合并高层区域密度相近的水汽，保证了垂直分层的精度和真实性，且该方法适用于任意层析区域，即使在水汽垂直分布特征发生改变的情况下，也能迅速根据改变后的水汽垂直分布特征自动进行所需分层数的自适应非均匀分层，具有极强的适用性。

图2 自适应非均匀指数分层 Fig.2 Adaptive non-uniform exponential vertical stratification

3 GNSS水汽层析试验验证

3.1 试验区域及时段

本文以香港为试验区域，图3为试验区域内参考站及探空气象站分布图，其中实心圆图形表示19个参考站所在位置，实心三角形图形表示探空气象站所在位置。本文利用19个连续运行参考站(continuously operating reference system，CORS)的GPS观测数据进行水汽层析试验，以京士柏探空气象站(HKKP)的探空(radiosonde，RS)数据为参考，将HKKP位置天顶方向的层析水汽密度与探空水汽密度进行对比分析。

图3 香港地区参考站及探空站地理位置Fig.3 Geographic distribution of the Hong Kong SatRef with GNSS reference stations and radiosonde

试验时段选取2019年8月(31d)，试验时段内香港地区正值夏季，气候炎热，且由于受热带气旋“韦帕”及“白鹿”的影响，共发生3次大规模降雨，因此香港2019年8月同时具备了暴雨和炎热无雨的不同水汽情况，十分适宜进行水汽层析试验。

3.2 试验方案设置

观测值SWD的获取使用GAMIT10.7对GPS观测数据进行处理，为消除多路径效应的影响，将卫星截止高度角设置为15°；引入固体潮模型和海潮模型进行改正；映射函数模型设置为VMF1；引入BJFS、CHAN、USUD 3个外网辅助IGS站进行联合解算以削弱天顶对流层延迟(zenith total delay，ZTD)的相关性。

层析方程组的解算采用ART技术。该技术中迭代初值的精度对层析结果的准确性具有重要影响，高精度的迭代初值可同时提高迭代速度和层析结果质量。本文根据香港地区2010—2018年探空数据计算获得的不同年份8月全部垂直水汽廓线均值作为迭代初值进行层析试验[27]。

由于在试验时段内只能获取每日UTC 00∶00时和UTC 12∶00时的探空数据作为参考，故每日只选取UTC 00∶00时和UTC 12∶00时两个时段进行水汽层析试验。本文以水汽密度等于0.1 g/m3的高度作为对流层层顶，通过试验时段内62次探空顶层高度的平均值确定试验区域顶层高度，经计算顶层高度平均值为10 770 m，标准差(standard deviation，STD)为935 m。水汽层析试验区域水平方向范围为22.204°N—22.564°N与113.844°E—114.384°E之间，水平分辨率为0.090°×0.090°[23]，垂直方向范围为地面至10 770 m之间，垂直分辨率由分层方案决定。

方案A：该方案基于传统均匀分层，均匀分层高度间隔在800 m时，可以获得较好的层析结果[5]，因此该方案将10 770 m高的层析区域分为13层，使每层间隔为828.5 m，最接近800 m。顶层约束的先验水汽密度以先验探空数据为依据，由于顶层约束值作为层析方程组的观测值直接参与三维水汽密度场的反演，不能采用试验时段内的探空数进行先验水汽密度的计算，且大气水汽存在周期性变化规律[30-33]，故采用试验年份前一年(2018年)同时段(夏季8月)的探空数据计算先验水汽密度，经计算，水汽密度均值为0.23 g/m3，故将顶层约束设置为0.23 g/m3。

方案B：该方案基于ANEVS，分层数设置为与方案A相同的13层。大气水汽的垂直分布特征函数采用先验探空水汽密度数据进行拟合。由于探空气象数据具有高精度、高垂直分辨率的优点，同时，以探空站点处的水汽密度信息代表探空站周围一定区域内大气水汽密度真值的可靠性已经被证实[34-36]，故探空站的垂直水汽密度廓线常被用作层析区域内水汽密度的参考真值，以辅助分析水汽层析的反演结果[7-8,37]。本文的层析试验区域属于小范围层析区域，基于高精度的先验探空水汽密度建立的水汽垂直分布模型在该层析区域内具备有效性。由于水汽垂直分布特征函数直接影响了观测方程系数矩阵的数值，因此作为先验信息的水汽垂直分布特征函数不能采用试验时段内的探空水汽密度数据进行拟合，基于大气水汽的周期性变化特征[30-33]，以试验年份前一年(2018年)同时段(夏季8月)的探空水汽密度作为先验信息在时间域上具备代表性，拟合后的指数函数表达式为

(14)

式中，Dw表示水汽密度值，单位为g/m3；h表示高度，单位为m。探空数据拟合后的R2为0.977 4；均方根误差(root mean squared error，RMSE)为0.919 g/m3。基于式(14)的水汽垂直分布特征函数对试验区域运用ANEVS进行垂直分层后，将0～1500 m以300 m为高度间隔划分5层，1500～10 770 m划分为剩余8层，每层水汽密度间隔约为1.70 g/m3，第6层为1500～1838 m，高度间隔338 m，大于300 m，经前一年同时段探空数据计算顶层水汽密度均值为0.87 g/m3，故将顶层约束设置为0.87 g/m3。

分别以方案A和方案B对试验区域进行垂直分层建模，图4为两种分层方案的分层建模示意图。

图4 方案A及方案B垂直分层模型的垂直分辨率设置Fig.4 The vertical resolution of the vertical stratification model of project A and project B

4 GNSS水汽层析试验结果分析

4.1 不同垂直分层方案的解算精度分析

图5为试验时段内UTC 00∶00时与UTC 12∶00时层析历元下两种方案的单天RMSE值对比图。其中方案A的RMSE数值最大出现在DOY 213 UTC 00∶00时(2.15 g/m3)，数值最小出现在DOY 214 UTC 12∶00时(0.70 g/m3)；方案B数值最大出现在DOY 233 UTC 00∶00时(1.83 g/m3)，数值最小出现在DOY 214 UTC 12∶00时(0.54 g/m3)。方案B有近50%的试验RMSE小于1 g/m3，而方案A仅4组试验RMSE小于1 g/m3，同时方案B有90%以上的RMSE小于方案A，故单天解精度对比中方案B明显优于方案A。

图5 层析时段内两种方案层析结果的RMSE对比Fig.5 Comparison of the RMSE of the tomography results derived from 2 projects during the tomography periods

本文以高精度和高垂直分辨率的探空水汽密度廓线信息为参考值，对整个试验数据集的层析结果进行整体精度评定，表1给出了两种方案层析结果的RMSE和MAE(mean absolute error)。由表1可知，方案B的两种统计量相比于方案A均具有更低数值，其中RMSE降低了0.401 g/m3，MAE降低了0.223 g/m3，说明ANEVS的整体解算精度高于均匀分层。

表1 两种方案的层析结果与探空数据对比的平均RMSE和平均MAETab.1 Average RMSE and average MAE of the tomography results derived from 2 projects using radiosonde data as a reference (g/m3)

图6为试验时段内，两种方案层析水汽密度与探空数据之间的散点图。如图6所示，方案B相较于方案A具有更强的聚集性，同时方案B具有更高的R2、更低的RMSE，拟合线性函数的斜率也更接近1，表明方案B解算结果质量优于方案A。对比两方案的散点图还可发现，方案B散点在20～25 g/m3区间内的聚集程度高于方案A，这是由于均匀分层于近地区域的水汽分层粗糙，底层间距大，水汽密度跳跃残缺，卫星信号利用率低，大幅降低了方案A底层的解算精度，导致底层解算精度与中间层解算精度相当，因此方案A的散点图于20～25 g/m3区间内的聚集程度十分接近5～20 g/m3区间，而方案B的底层水汽分层细致，信号利用率高，大幅提高了底层解算精度。下面本文将对两种方案在不同天气条件下和不同高度处的层析结果做进一步分析。

图6 两种方案层析反演水汽密度与探空水汽密度散点图Fig.6 Scatter plots of water vapor density between radiosonde and tomography derived from 2 projects

4.2 不同天气层析结果分析

图7为层析水汽密度廓线与探空水汽密度对比图，其中红色曲线和蓝色曲线分别表示方案A和方案B的垂直水汽廓线信息，绿色散点表示探空水汽密度信息。本文选取DOY 221 UTC 00∶00时和DOY 238 UTC 00∶00时的层析水汽廓线为例与探空数据进行验证分析，其中DOY 221最高温度达34.8℃，无降水活动发生，属于高温炎热的无雨天气；DOY 238由于受本月第二次强台风“白鹿”的影响出现持续大暴雨，属于暴雨天气。由图7可知，方案B与探空水汽密度具有更好的符合度，尤其在3000 m以下的高度区间内，方案B的水汽廓线能更好地反映水汽的真实情况。此外，对比两种方案在不同天气条件下的垂直水汽廓线可以发现，方案A在近地高度区间内仅能表现出大气水汽的整体变化趋势，其原因是在进行层析区域建模时，基于均匀分层的方案A在3000 m以下仅具有3层完整的分层区间，导致通过水汽层析技术反演获得的水汽密度参数数量较少，无法表现出大气水汽在恶劣天气条件下的波动现象，而基于ANEVS的方案B在3000 m以下具有8层完整的分层区间，充足的水汽密度参数使其具备了反映近地空间大气水汽波动现象的能力。

图7 两种方案的层析水汽廓线与探空水汽密度对比Fig.7 Comparison of tomographic water vapor profiles between 2 projects using the radiosonde as a reference

水汽密度廓线只具备表现天顶方向的垂直水汽密度信息的能力，并不能对三维水汽密度场进行展示，如图8所示，本节基于方案A和方案B的层析反演结果，展示了DOY 238 UTC 00∶00时三维水汽密度场的可视化结果。方案A与方案B相比，方案A中下边界处层与层之间的色阶变化明显，上边界处的色阶变化则较小，表明均匀分层反演的三维水汽密度信息具有下边界处匮乏而上边界处冗余的缺点，对比图中方案B反演的三维水汽场可发现，ANEVS弥补了均匀分层的不足，其色阶变化丰富，具有更精确的水汽密度信息反演能力。

图8 两种方案的三维水汽密度场可视化Fig.8 Visualization of three dimensional water vapor density field derived from 2 projects

表2为DOY 221和DOY 238不同方案层析水汽密度与探空水汽密度的相关系数。在无雨日(DOY 221)和降雨日(DOY 238)的对比中，两种方案均在无雨天气情况下具有更高的相关系数，说明恶劣天气一定程度上影响了层析结果的质量；在两种方案之间的对比中，不同天气条件下方案B的相关系数均高于方案A，表明ANEVS相比于传统均匀分层具有更优质的大气水汽反演效果；对比两种天气条件下不同方案间的相关系数之差可发现，在水汽不稳定的恶劣天气，方案B对于相关系数的提高量大于水汽稳定的无雨天气，说明方案B在恶劣天气条件下能更好地优化大气水汽的反演效果。

4.3 不同高度层析结果分析

图9给出了两种方案的层析结果在每1层上与探空数据对比的RMSE。从图中可看出，两种分层方案的各层RMSE均呈现先增大再减小的变化规律，在方案B中所有分层的RMSE均小于1.5 g/m3，而方案A中1～5层的RMSE大于1.5 g/m3，其中第2层的RMSE大于2.5 g/m3，表明方案A于低海拔处的层析解算结果质量较低。从两种方案的各层RMSE对比中还可发现，方案A中9～11层的RMSE小于1 g/m3，而方案B中对应层数的RMSE大于1 g/m3，产生此现象的原因是两种方案在分层数相同的情况下，每1层所对应的实际高度区间不同，分层层数越大，两个方案之间的实际高度区间相差越大。由4.2节可知，分层数9～11层于方案A中实际对应6628～9113.5 m，于方案B中其实际对应2688～4982 m，而6628～9113.5 m区间内的实际水汽含量相较于2688～4982 m区间内的小很多，导致方案A的RMSE在9～11层小于方案B。因此，为了进一步对比两种方案的垂直精度，图9还给出了方案A和方案B在各高度处的RMSE对比图。由图9可知，方案A于4000 m以下的解算精度明显低于方案B，这是由于方案A低海拔处分层粗糙，不符合大气水汽的垂直分布特征，卫星信号利用率低下，大幅降低了层析解算精度；4000 m以上两种方案精度相当，即使方案A于高海拔处分层更精细，但由于卫星信号分布稀疏、水汽稀薄，解算精度并未得到实质性提高。方案B使用ANEVS由于考虑到水汽的垂直变化特征，以水汽密度区间为分层准则，该方法获得的非均匀高度区间使各层水汽密度变化控制在一个较小的范围内，同时这种非均匀高度区间还适应了卫星信号呈倒锥形发散的特征，在保证了高海拔处解算绝对误差较小的同时，大幅提高了低海拔处的解算精度。

图9 两种方案层析结果与探空数据对比的各分层RMSEFig.9 RMSE at each layer of the tomographic results derived from 2 projects using the radiosonde as a reference

大气水汽整体表现出高层稀薄、底层充沛的特点，这种现象使高层水汽密度的绝对误差相较于其他位置小很多，再加上传统均匀分层将过多的层次划分至绝对误差本就较小的高层区域内，因此使用与绝对误差相关的统计量评定解算精度可能造成误判，对此本文额外使用相对误差(relative error，RE)对层析结果进行评定。相对误差表示为绝对误差与真值的比值，计算公式为

(15)

式中，RE表示相对误差(%)；DT表示水汽层析反演水汽密度值，单位为g/m3；DRS表示利用探空数据计算得到的水汽密度值，单位为g/m3。

相对误差能更好地考虑真值本身的数量级，用百分比的形式对误差进行归一化处理，因此在研究不同垂直分层方法之间解算精度时使用相对误差具有更好的真实性和可比性。如图10所示，两种方案的各层平均相对误差(mean relative error，MRE)均随高度增加而增加，表明解算精度随高度增加而递减。在2500 m以下的高度区间内，两种方案的MRE均小于20%，解算精度较高，ANEVS的MRE在2000 m以下小于10%，在1000 m以下小于5%，精度可达传统均匀分层的2倍以上，具有更高的解算精度；在2500～4500 m的高度区间内，两种方案的解算精度同时随高度增加而降低，但方案B的精度仍稍优于方案A。由图10还可以发现，方案A只有1～7层MRE小于100%，8～13层MRE均大于100%，说明传统均匀分层并未切实提高高层区域的解算精度；方案B仅最顶层MRE超过100%，倒数第2层MRE接近40%，其余层MRE数值更小，ANEVS细致的低层层次划分适应了大气水汽的分布特征，充分高效地利用了低海拔密集的卫星信号观测值，水汽层析解算效率远高于方案A。综上，在以MRE为依据的解算精度对比上，ANEVS相比于传统均匀分层有很大提高，该方法能将低海拔水汽进行细分，控制各层水汽密度差异，提高卫星信号的利用率，将高海拔处密度相近的水汽归并为同一层次，减少了高层水汽解算的多余工作，在自适应地进行大气水汽垂直分层的同时，克服了传统均匀分层方案的缺点。

图10 两种方案层析结果与探空数据对比的各层MREFig.10 MRE at each layer of the tomographic results derived from 2 projects using the radiosonde as a reference

5 结 语

本文提出了一种基于大气水汽垂直分布特征的自适应非均匀指数垂直分层方法(ANEVS)。ANEVS以水汽密度区间和水汽垂直分布特征函数反推垂直分层高度区间，再通过迭代自适应地调整高度区间，以缩小各层之间的水汽密度差异，使分层高度区间满足实际水汽变化规律，实现对任意给定层析区域进行任意分层层数的自适应非均匀分层，该非均匀分层方法在具备科学可靠分层依据的同时又具有方便快捷且自适应的优势。本文利用香港CORS网2019年8月的GNSS观测数据对比分析了ANEVS与传统均匀分层的层析结果的质量及精度，得到以下结论。

(1)ANEVS在层析结果的精度与质量上均优于传统均匀分层。在散点图的对比上，ANEVS表现出更强的聚集性，同时ANEVS散点图具有更高的确定系数和更低的均方根误差，ANEVS层析结果的均方根误差和平均绝对误差相较于传统均匀分层分别降低0.401 g/m3和0.223 g/m3。

(2)在不同天气条件下，ANEVS水汽廓线能更好地反映水汽的垂直扰动变化。不同天气下ANEVS水汽密度与探空水汽密度的相关系数均高于传统均匀分层，在暴雨天气下两种方法的相关系数之差大于无雨天气，表明ANEVS在恶劣天气条件下对大气水汽反演效果的优化更加显著。

(3)在不同高度的层析结果对比中，ANEVS对低层高度区间内层析结果精度的提高更加显著。在分层数同为13层的条件下，传统均匀分层的平均相对误差有6层高于100%，仅1～7层小于50%，ANEVS的平均相对误差仅最顶层1层高于100%，1～9层小于20%，ANEVS的均方根误差于4000 m以下的高度区间内显著减小，表明ANEVS大幅提高了各层层析结果的解算质量，其中低层层析结果质量的提升尤为显著。

笔者后续的研究与工作内容主要包括两方面：一方面是调整并扩大层析试验区域，以便引入复数个探空气象站的数据，对大气水汽垂直分布特征模型的有效覆盖范围进行定量分析；另一方面，基于对先验大气水汽密度进行长时间跨度的统计学分析，研究并总结出一种能够适用于不同月份的表示大气水汽垂直分布特征的建模准则。

致谢：特别感谢香港地政总署测绘处提供的香港卫星定位参考站网络的GNSS观测数据(https:∥www.geodetic.gov.hk/en/satref/satref.htm)，香港King 's Park天文台提供的京士柏气象站的无线电探空数据(http:∥weather.uwyo.edu/upperair/sounding.html)，麻省理工学院地球大气和行星科学系提供的GAMIT/GLOBK软件。