无监督密集匹配特征提取网络性能分析

金 飞，官 恺，，刘 智，韩佳容，芮 杰，李庆高

1.信息工程大学地理空间信息学院，河南 郑州 450001；2.西安测绘总站，陕西 西安 710054

密集匹配在众多领域都有着重要的应用，如无人驾驶[1]、工业自动化及航空测绘[2-3]等领域。其原理是通过寻找左右图片每个像素的同名点来形成密集的视差图，然后根据相机内方位元素和基线长度计算得出距离信息。因此，密集匹配的质量将直接影响测距的精度。

传统匹配方法需要经过特征提取、匹配代价聚合、视差计算、视差精化[4]4个步骤。在相当长的一段时间里，传统匹配方法占据了主导地位，且广泛应用于生产生活中，比如局部匹配算法中绝对值差(sum of absolute differences,SAD)[4]、灰度平方差(sum of squared differences,SSD)[5]等，全局匹配算法中的动态规划法[6]、图割法[7]等，以及多个改进版本已实现商用化应用的半全局算法(semi-global matching,SGM)[8]。这些传统方法虽各具特色，但仍需人工设计特征描述符，无法基于数据驱动进行特征描述符自学习，在精度和稳健性提升方面具有较大的局限性。

随着计算机硬件的发展和深度学习方法的不断完善，MC-CNN[9]将卷积神经网络应用于密集匹配，利用深度学习数据驱动的优势，选出了更具稳健性的特征；DispNet[10]以光流预测网络FlowNet[11]为基础，改进了其上采样过程后应用于密集匹配，是首个端到端的密集匹配网络；iResNet[12]在DispNet基础上增加了多尺度信息，并采用了贝叶斯网络精化视差；GCNet[13]利用深度学习框架模仿传统匹配流程，并在传统的深度学习网络中引入了视差软回归[14](soft argmax)，替代了原先不可导的取最大值下标的函数(argmax)，将视差分类转变为视差回归，大大地提升了匹配精度；PSMNet[15]在GCNet的基础上引入了金字塔池化[16]，进一步融合了多尺度信息，同时还加入了堆叠沙漏模块[17]，使不同位置的特征可以相互参考，并将本级参考的特征传入到下一级。

虽然监督方法在计算机视觉领域已经取得了相当不错的成就，但在航空摄影测量领域，受各种条件的制约视差标签数据获取困难，且训练过程对标签精度依赖程度高，同时不同场景的特征并不完全一致，该方法应用于新的数据集，标签数据的获取将会制约深度学习在该领域的应用。

相比于有监督方法，无监督方法是未来发展的趋势。该领域已经有了一定的研究成果，文献[18]提出了一种可微的图像重构损失，使网络可以进行端到端训练；文献[19]提出了平滑损失函数，进一步提升了模型的稳定性；文献[20]采用空间变换网络(spatial transformer network,STN)[21]对图像进行重构，并引入左右一致性以提高模型预测精度；文献[22]在重构损失函数基础上引入了一阶差分，并将平滑损失函数改为了二阶平滑，同时还引入了最大深度搜索损失函数；文献[23]改进了平滑损失函数，使得平滑阈值从绝对变为相对，同时提出了共视区概念，通过掩膜掉遮挡区域和边缘非重叠区域的方式进一步提升了匹配精度。

上述文献重点研究网络结构或损失函数，而对于无监督训练条件下不同的网络结构对精度的影响缺乏进一步研究；同时，现有的公开研究中，无监督方法试验的数据集均为近景，针对航空影像数据集的无监督匹配试验未见报道。本文将针对上述两个问题，分别采用航空影像和作为参照的近景数据集开展不同网络结构的精度测试分析，探究网络结构模块对匹配精度的影响。

1 本文方法

1.1 无监督网络框架构成

无监督网络框架由有监督网络结构和无监督损失函数共同构成，如图1所示。输入图像首先通过有监督网络结构生成左视差图；然后，将图像进行水平翻转并交换左右图位置输入到网络中，生成翻转的右视差图，通过左图、右图、左视差图及右视差图，分别构建重构左图、重构右图、重构左视差图和重构右视差图；最后，据重构损失函数、平滑损失函数以及左右一致性损失函数进行网络的反馈训练。

图1 无监督网络框架Fig.1 Unsupervised network framework

1.2 有监督网络结构

有监督网络结构采用有监督网络除损失函数外的部分，涉及的网络结构包括DispNet、iResNet、GCNet和PSMNet，大致可分为两类：DispNet和iResNet属于经典全卷积网络，匹配过程完全依靠卷积网络参数拟合；GCNet和PSMNet则通过模仿传统匹配流程，在匹配过程中构建匹配代价并计算视差形成视差图。

1.2.1 DispNet

DispNet网络由FlowNet网络改进得到，整体结构为全卷积网络，分为特征提取端和分辨率恢复端，中间设置跳层结构，网络可看作U-Net结构。类似于FlowNet的FlowNetS和FlowNetC两个不同版本，DispNet也分为DispNetS和DispNetC两个对应的版本，如图2所示，DispNetS与DispNetC的差异体现在特征提取端的前半部分，前者是将左右图在通道维进行叠加，后者采用孪生网络[24]形式，左右图片先分别提取特征，并同时提取相关特征图，二者叠加后继续进行特征提取和分辨率恢复。相较于其他网络结构，DispNet的网络结简单，运算速度快。

图2 DispNet结构Fig.2 DispNet structure

1.2.2 iResNet

iResNet网络引入了多尺度特征，这些多尺度特征与网络主体部分输出的结果融合形成初始视差图，然后通过迭代精化的方式提升初始视差图精度，结构如图3所示。在特征提取部分，网络主体部分按照类似于DispNetS的方式进行下采样和特征提取，多尺度部分则在特征初步提取后进行上采样，并再次进行特征提取；随后将两部分的结果合并作为初始视差，并通过贝叶斯估计的重构迭代精化模块提升视差精度，形成最终的视差图。

图3 iResNet结构Fig.3 iResNet structure

1.2.3 GCNet

GCNet通过深度学习框架实现了端到端的学习，无须其他后处理，如图4所示，其步骤为：①特征提取，GCNet通过追加多个残差块的方式增加孪生网络深度，使得网络能够提取到更高级别的特征；②匹配代价构建，在提取左右特征图后，构建匹配代价，即左右特征图合并叠加，每合并一次，右图相对于左图沿基线方向平移p个像素，直至到达最大视差Dmax，共平移Dmax/p次，共有Dmax/p个左右合并的特征图在视差维进行叠加；③视差计算，通过三维卷积提取特征图在平面以及视差维的特征，形成匹配代价；④视差软回归，匹配代价通过softmax映射为概率，再通过soft argmax的方式计算最终视差值。

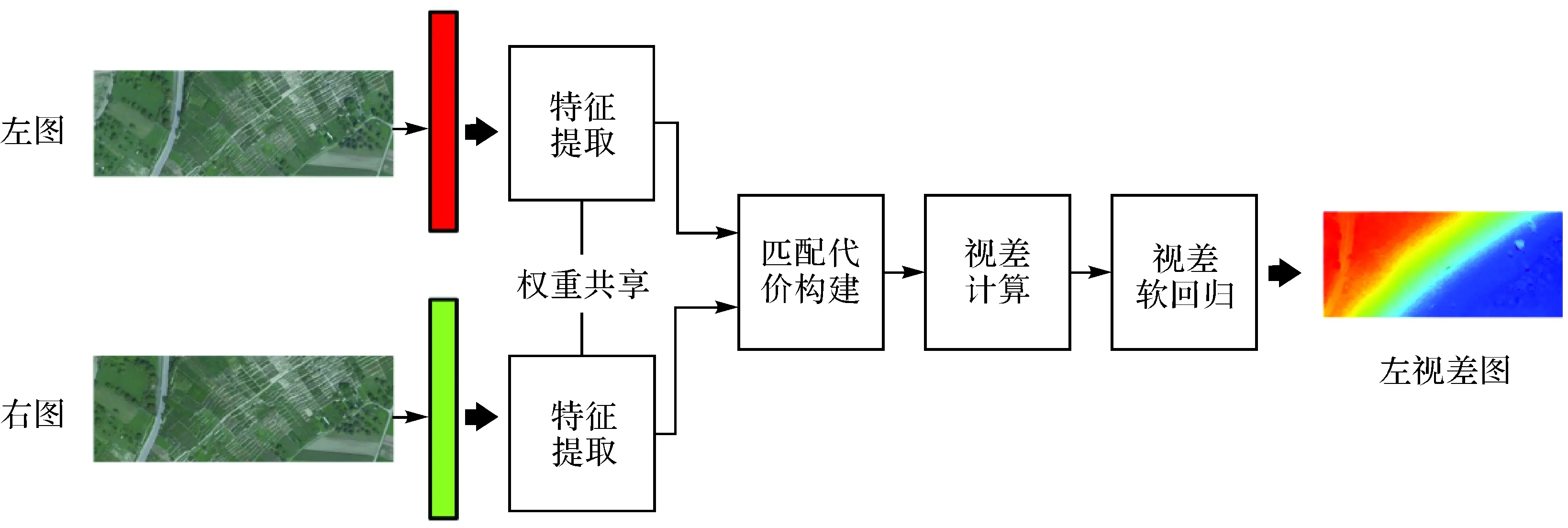
图4 GCNet结构Fig.4 GCNet structure

整个网络由于使用了较多的残差块，且涉及构建四维张量块(通道、视差、高度、宽度)和三维卷积，网络速度相对较慢。

1.2.4 PSMNet

PSMNet沿用了GCNet架构。为解决GCNet因“视野”不足而导致的稳健性问题，在特征提取部分和匹配代价构建部分之间增加了金字塔池化模块，并在代价计算过程利用堆叠沙漏模块替换传统的三维卷积模块。金字塔池化部分首先对提取的特征图分别进行64×64、32×32、16×16、8×8的池化，然后将池化后的特征图、未池化的特征图以及特征粗提取的特征图在通道维进行合并，最后经过卷积融合，形成匹配代价构建所需的特征图。沙漏模块具有特征位置相互参考的功能，通过多个沙漏模型的堆叠，效果优于普通三维卷积。PSMNet在其消融试验过程中存在多个版本，本文分别选用视差计算部分为三维卷积模块的PSMNetB和采用堆叠沙漏模块的PSMNetS(图5)。

图5 PSMNet结构Fig.5 PSMNet structure

1.3 无监督损失函数

本文重点探讨无监督条件下网络结构对匹配精度的影响。为消除无监督方法中损失函数改变对精度带来的影响，损失函数统一采用文献[20]中所提到的损失函数，包括重构损失函数、平滑损失函数及左右一致性损失函数，其总损失函数可定义为

C=wapCap+wdsCds+wlrClr

(1)

式中，w为损失函数权重；C表示损失函数；下标ap表示重构，ds表示平滑，lr表示左右一致。

为便于损失函数的说明，设I为输入图像矩阵，D为视差预测图，下标L、R分别表示左右图像，则左视差图DL与输入图像IL、IR之间的关系可表示为

DL=FNet(θ;IL,IR)

(2)

式中，FNet为有监督网络结构；θ表示网络的参数。

将原始图像作水平方向的翻转变换，变换后的左图变为右图，右图变为左图，分别输入网络中，则可以生成水平方向翻转后的右视差图，再做一次翻转变换后，得到右视差图，其过程可通过式(3)表示

DR=Ffilp〈FNet[θ;Ffilp(IL),Ffilp(IR)]〉

(3)

式中，Ffilp为水平方向翻转函数。

1.3.1 重构损失函数

(4)

式中，Fgrid表示由视差图生成采样格网的函数；上标wrap表示重构。

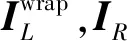
(5)

式中，FSSIM[25]表示图像相似度函数；α为权重调节因子，通常设置为0.85。

1.3.2 平滑损失函数

重构损失虽然能够对图像形成一定约束，但是在图像的重复纹理、弱纹理以及无纹理区域，该损失函数无法及时发现误匹配，因此需要通过平滑损失函数辅助约束。平滑损失函数利用原始图像对视差图进行约束，其核心思想是通过图像的纹理变化来约束视差的变化，即在视差变化大的区域，图像像素值也应当有较大变化，反之则需要进行约束。平滑损失函由原图像I的一阶差分对视差图D的一阶差分进行加权得到，加权的形式为e的负指数形式，其损失函数定义为

Cds=Favg[|∇xD|e-|∇xI|+|∇yD|e-|∇yI|]

(6)

式中，差分公式如下

∇dM=Favg[(Md+1-M)+(Md+1-M)]

(7)

式中，M表示二维矩阵；∇表示一阶差分；d表示方向，包括x、y两个方向。

1.3.3 左右一致性损失函数

与重构图像的方法类似，重构视差图通过STN网络进行构建，其定义为

(8)

在重叠区域，左右视差图理论上应当是一致的，因此可以通过左右一致性进行约束，其定义为

Clr=Favg(|D-Dwrap|)

(9)

2 数据集

为全面评价网络的性能，试验共采用4个数据集，其中两个为航空影像数据集，分别是Vaihingen和WHU，另外两个近景KITTI数据集作为参照组共同参与测试。

2.1 Vaihingen数据集

Vaihingen数据集[26]为德国乡村航空场景，包含3条航带36张乡村影像，图像大小为9240×14 430像素，航向重叠度和旁向重叠度均为60%，图像整体区域平坦，高层建筑较少，大部分为植被和密集低矮的房屋。数据集标签是由多套商业软件匹配出的DSM数据取平均后依据内外方位元素反算得到的半稠密视差图，裁切后的图像大小为955×360像素，共731对。

2.2 WHU数据集

WHU数据集[27]为贵州乡村无人机场景，包括高楼大厦、少量的工厂以及一些山脉、河流等，拍摄航高为550 m，地面分辨率10 cm，航向重叠率90%，旁向重叠率80%，共1776张5376×5376像素的图像，对应1776视差真值图。经过整理和裁切，实际使用数据包含8316张训练图片和2663张测试图片，图像尺寸为768×384像素。

2.3 KITTI数据集

KITTI数据集[28-29]为真实场景的汽车驾驶数据集，包含KITTI2012和KITTI2015两个子集，前者包含194对训练图像和195对测试图像，图像大小为1226×370像素；后者包含200对训练图像和200对测试图像，图像大小为1242×375像素。

3 试验与分析

试验在Windows 10操作系统下进行，通过Anaconda创建虚拟环境，采用PyTorch[30]深度学习框架，显卡为1080Ti，显存11 GB。受显存限制，参数batchsize通过梯度累加模拟实现，设置为8，优化器为Adam[31]，β1=0.9，β2=0.999。由于密集匹配网络对内存需求大，在训练过程中需要存储梯度，因此训练过程将原始图像随机裁剪为512×256像素大小的图片，该操作一方面可以节约内存，另一方面能够增强数据集。

参数指标分别为终点误差(end point error,EPE)和3像素误差(3 pixel error,3PE)。EPE为所有像素预测视差与真实值之差绝对值的平均值；3PE为预测值与真实值误差大于3像素占图像所有参与预测点总数的百分比。两个标准均为值越小，匹配效果越好。

3.1 各网络结构匹配能力试验

为探究网络结构对视差精度的影响，在相同的损失函数条件下，分别选用DispNetS、DispNetC、GCNet、iResNet、PSMNetB及PSMNetS网络结构进行测试，最大视差统一为192像素，计算误差时仅统计视差小于192的像素点；损失函数权重比例为wap=1.0,wds=0.001,wlr=0.001；采用的数据集为Vaihingen、WHU、KITTI2012和KITTI2015数据集的训练集，训练轮次上限为2000轮。由于测试过程中网络收敛速度各不相同，因此在损失函数值和测试精度均不再明显下降时判定网络收敛，并结束训练。在实际测试中，对于EPE和3PE出现最小值轮次不一致的情况，两个指标分别在所有测试轮次上取各自的最小值。考虑到边缘非重叠区不符合损失函数约束，且误差较大，影响误差评价，故将左视差图的左侧非重叠部分裁去最大视差192个像素后，重新对视差图进行精度评估，结果见表1。

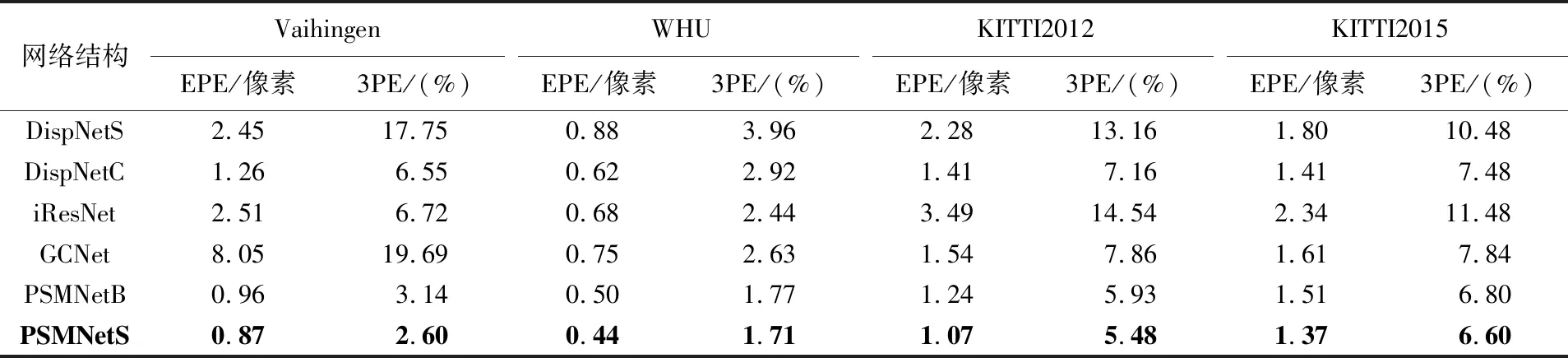
表1 无监督条件下裁切非重叠边缘区域后各网络精度Tab.1 Accuracy of each networks after cutting non-overlapping edge area under unsupervised condition

由表1可知，从精度角度来看，PSMNet的两个网络精度和稳健性分列第1、第2位，其中，PSMNetS的精度更高，在两个航空影像数据集上，EPE均在1像素内，而3PE均在3%以内，具有一定的实用价值。此外，考虑目前的损失函数并不一定是最优的，其精度仍有提升的潜在可能。

3.2 与有监督训练的关系

为了比较相同网络结构在有监督方法和无监督方法下的区别，可以通过观察这些网络在有监督条件下与在无监督条件下精度是否排序一致的方式进行判断。考虑到各个论文中的匹配精度采用了不同的训练方法，参数设置也各不相同，且未裁切边缘非重叠区域，因此需要在相同的环境下用有监督的方法进行验证，试验结果见表2。

为了进一步分析非重叠区域裁切对精度的影响，同时验证本文有监督试验结果(表2)的有效性，需要对比本文监督方法(表2)和已经公开方法(表3)之间的精度排序。首先通过KITTI官网和相关论文[10,12-13,15]查询到了参与的网络在KITTI和SceneFlow数据集上的精度，结果见表3，其中，train表示从原始训练集中划分出的验证集，test表示测试集。

表2 监督条件下裁切非重叠边缘区域后各网络精度Tab.2 Accuracy of each networks after cutting non-overlapping edge area under supervised condition

表3 监督条件下各网络精度的公开结果Tab.3 Disclosure results of the accuracy of each network under supervised condition (%)

由表3中的KITTI2012和2015数据集的测试集可以推断出PSMNetS精度最高，然后依次是iResNet、GCNet、DispNetC；由KITTI2012和2015数据集的验证集可以推出DispNetC的精度高于DispNetS；通过SceneFlow数据集可以推出PSMNetB的精度介于iResNet与PSMNetS之间。综上所述，按照目前已经公开的精度，网络结构的匹配能力从高到低依次是PSMNetS、PSMNetB、iResNet、GCNet、DispNetC和DispNetS。

结合表1、表2和表3进行综合排序，其中表3排序已经给出，表1和表2排序以每个网络在4个数据集上EPE之和作为排序依据，EPE越低则排名越靠前，按照此标准排序结果如下。

比较表4中论文公开精度和仅考虑表2中KITTI数据集的有监督方法，首先发现两者在排序上是一致的，说明裁切图像非重叠边缘对视差图的排序是没有影响的；其次，比较仅考虑KITTI数据集的有监督方法和加入航空数据集后的有监督方法，发现排序产生了变动，GCNet的排序从第3位滑落至低5位，结合表1可知，GCNet在两个航空数据集上表现较差，此外，iResNet和DispNetC的位置发生了变化，但两个网络之间EPE差异仅为0.04像素，且在仅计算KITTI数据集的精度条件下也仅相差0.04像素，考虑到深度学习训练的随机性，可以忽略不计；最后，比较有监督方法(表2)和无监督方法(表1)可以发现除了GCNet之外，iResNet网络的精度也在出现了大幅度下滑。这两个异常现象会在后文进一步分析。

表4 多种方法的排序结果Tab.4 Sorting results of multiple methods

3.3 网络结构子模块对精度的影响分析

3.2节分析了相同的网络结构在有监督和无监督训练条件下的区别，但是仅从网络整体上无法进一步分析无监督条件下，网络子模块对精度的具体影响，这对进一步设计网络结构是不利的，因此需要对网络结构进行分解，具体分析网络各个子模块所起作用。通过比较参与测试网络结构之间的差异归纳出多个网络子模块，包括孪生网络、相关信息提取融合、残差块提取特征、多尺度信息、视差迭代精化、三维卷积和堆叠沙漏模块，见表5，从中可看出个网络结构之间的模块差异。

表5 不同网络结构差异Tab.5 Different network structures differ

按照表5可进一步分析网络结构子模块和匹配精度的关系，具体如下。

(1)孪生网络模块和相关信息融合可较大幅度提升精度。DispNetC与DispNetS之间的差异集中在孪生网络和相关信息提取，由表1和表2可知，DispNetC精度高于DispNetS，说明孪生网络和相关信息融合模块在无监督条件下依然对精度有提升作用。

更进一步，为探究孪生网络与相关信息融合是否均起到了提升作用，本文进行了试验验证。去掉DispNetC中的相关信息提取模块，两个特征图直接在通道维进行拼接，构成DispNetNoC网络结构，结果见表6。

表6 孪生网络和相关特征提取作用结果Tab.6 Results of siamese network and related feature extraction

从试验结果可以看出，DispNetNoC的精度介于DispNetS与DispNetC之间，说明无监督条件下，孪生网络和相关信息提取模块均会提升匹配精度。

(2)多尺度信息对稳健性和精度均有提升作用。PSMNetB与GCNet网络结构区别在于特征提取部分，前者通过孔洞卷积和金字塔池化优化了特征提取部分，进一步强化了网络多尺度信息的提取能力，由表1中精度结果可知，多尺度信息对精度有较大提升，3PE平均提升5.1个百分点。

通过探究GCNet数据异常原因，可侧面印证全局信息的作用。试验将生成结果与标签数据作差取绝对值，形成误差图。对整个数据集所有图像进行误差统计后发现，由于缺少全局信息，GCNet在农田、水泥路等大面积平滑和重复纹理的区域表现极差，如图6(a)所示，而对于有一定纹理的区域表现较好，如图6(b)所示，但在其右下角有一处较为平滑的区域，产生了较大的误差。由于Vaihingen数据集为乡村地区，农田等大面积平滑区域较多，大多数场景类似于图6(b)，导致整个数据集精度极差，由此可知全局信息对于精度的和稳健性具有十分重要的作用。

图6 GCNet在Vaihingen数据集上的误差Fig.6 Error graph for GCNet on the Vaihingen dataset

(3)堆叠沙漏模块优于三维卷积模块。PSMNetS网络结构与PSMNetB网络结构的差异在于视差计算部分，PSMNetB采用三维卷积模块，PSMNetS采用堆叠沙漏模块，由表1可知，PSMNetS精度在各个数据集上略好于PSMNetB，说明堆叠沙漏模块在该框架下优于三维卷积。

(4)重构方式的视差精化和重构损失函数重复约束，导致“负优化”作用。在有监督条件下，表现较好的iResNet网络结构在无监督条件下精度严重下降，对其进行进一步探究发现，iResNet网络结构在其尾部增加了视差精化模块，该模块利用重构迭代的方法对生成的视差图进行精化，该方式与重构损失函数重复约束，因而产生了“负优化”作用。为验证假设，将该部分移除后重新测试。作为对比，分别测试移除该模块(iResNet-0)、迭代1次、迭代2次和迭代3次的结果，见表7。

表7 iResNet网络结构精化模块迭代次数消融的试验结果Tab.7 Experimental results of iterative number ablation of the iResNet network structure elaboration module

经过试验验证，发现移除视差精化模块后，整个网络有近一倍的精度提升，说明精度降低确实是由于该模块导致的。同时，由于去除了视差精化模块，使其失去了视差精化的功能，在两个KITTI数据集上精度略低于GCNet。据此可知，重复约束会使无监督网络精度降低。

3.4 运行性能分析

网络运行性能是实用化的重要参考指标。监督方法利用模型的泛化性能，通常在训练完成后直接生成模型进行测试，因此通常只注重预测时间；而无监督方法直接在测试集上构建模型，需要考虑训练的总耗时。训练总耗时不仅由单次迭代耗时决定，同时也由模型的收敛速度决定，因此需要综合考虑。表8列出了各网络的运行性能，测试CPU为i7-7800X，GPU为GTX 1080Ti，数据集为KITTI2015，其中参数数量中M表示1×106，占用显存为batchsize=1时的显存占用情况，训练时间指在512×256像素的图像上迭代一次所花费的平均时间，预测时间指在KITTI2015数据集上预测一幅完整视差图所需要的时间，最优轮次指3PE达到最低值所需的轮次。

表8 网络运行性能Tab.8 Network performance

从参数数量和占用显存来看，DispNetS、DispNetC和iResNet等经典全卷积网络参数数量明显多于以GCNet为代表的密集匹配专用网络，参数量约为后者的10倍，但是GCNet等网络由于在训练过程中涉及四维张量(通道、视差、高度、宽度)，需要存储如梯度等大量中间计算过程，导致显存占用明显多于DispNet等网络。

从训练时间和收敛速度来看，DispNet等网络由于参数众多，收敛速度慢；而GCNet等网络虽然单次迭代耗时多于经典卷积网络，但收敛速度快，反而在全流程上更节约时间，最终耗时少于经典的全卷积网络。综上所述，在参与测试的网络结构中，PSMNetS不仅精度最高，而且达到最优精度的训练耗时也相对较少，虽然预测效率上略显不足，但对于非实时需求，仍可完全满足。

4 结 论

本文在无监督条件下，研究分析了密集匹配网络结构对匹配精度的影响，并分别在航空数据集和作为参照组的KITTI数据集上进行了试验。首先，验证了无监督方法在航测数据集上进一步应用的可能性，其整体精度与近景相近，其中PSMNetS网络结构效果最佳，具有较高的精度和稳健性；其次，分析得知在有监督条件下精度更高的网络结构在无监督条件下精度不一定也高，其精度不仅与网络结构自身的匹配能力相关，同时也与损失函数的兼容性存在一定关系；然后，进一步分析了无监督条件下网络模块和匹配精度的关系，其中，孪生网络、相关信息融合、金字塔池化、三维卷积以及堆叠沙漏模块均可增加匹配精度，而通过重构方式的视差精化模块则与重构损失函数重复约束，则起到了“负优化”作用；最后，分析了各个网络结构的运行性能，进一步验证了PSMNetS的实用价值。以上基于试验分析总结的结论，为进一步探索深度学习在测绘领域的实用化应用提供了重要的参考价值。

致谢:Vaihingen数据集和WHU数据集由武汉大学刘瑾同学提供，特此感谢。