基于弹性网约束的稳健变量选择
魏 双 微
(重庆师范大学 数学科学学院,重庆 401331)
0 引 言
当前社会数据海量、信息纷繁,如何从广大数据中寻找出有效信息已经成为学者们正在探讨的话题。因此,国内外学者先后提出了赤池信息准则、贝叶斯信息准则、广义交叉验证等方法来解决这一难题。这些方法不但缺乏稳定性,而且在自变量个数较多时还会耗费巨大的计算成本。寻找一种新的理论方法来解决高维数据的信息提取已然成为研究者们迫切需要解决的问题。Tibsniran[1]在惩罚函数的启发下提出了LASSO(Least Absolute Shrinkage and Selection Operator)估计,该方法在惩罚参数的合理选择范围内可以压缩某些分量至零以实现变量选择,并进行参数估计;Fan等[2]提出了惩罚似然函数的变量选择方法。然而,已有的文献大多是基于极大似然或最小平方进行研究和分析的,所得估计并不稳健。此外,这些方法不仅对于异常值很敏感,而且当误差为厚尾分布时估计效率会大大降低。因此,研究高维数据下估计方法更为稳健和有效就显得尤为重要。
Jaeckel[3]提出秩回归(Rank Regression)估计,其具备良好的稳健性和有效性;Wang等[4]结合加权SCAD(Smoothly Clipped Absolute Deviation)惩罚将秩估计推广到了固定维数参数模型下,并已证明该方法具有Oracle性质(即模型选择的相合性、参数估计渐近正态性);Wang等[5]通过局部秩估计对β(·)的稳健推断问题进行了研究,结果表明:在误差是非正态分布情形下,此方法能够显著地改善经典局部最小二乘估计;Yang等[6]基于B样条基近似非参函数并利用SCAD罚函数惩罚秩回归,提出了一种新的稳健估计,此方法能够进行变量选择以及识别变系数与常系数;Kwessi[7]将秩估计引入半参数模型下,结合自适应LASSO惩罚表明在重尾分布下所得估计量是一致的,并给出了渐近正态性结果。
Zou等[8]提出了弹性网方法,该方法可以处理协变量中出现的复共线性问题,其预测精度远远优于Lasso;卢[9]将Zou 等[8]的方法推广到了Logistic模型和Poisson模型中,证明该方法可将具有强相关性的变量全部选入模型或者剔除;黄[10]将Zou 等[8]的方法推广到部分线性模型中,同时提出并证明其具有Oracle性质;在超高维数据下,Xiao等[11]提出MSA-Enet(Multi-step Adaptive Elastic Net)方法进行降维,其目的是让变量维数小于样本容量;李[12]将Zou等[8]的方法应用到平衡纵向数据模型的变量选择中,证明了该方法具有相合性和组效应性质;Li等[13]将非负自适应弹性网估计推广到高维稀疏线性模型中,并在一些正则条件下证明了其Oracle性质和在有效样本下的有效性;王等[14]结合分位数回归和弹性网估计研究了基金绩效评价,且表明弹性网分位数回归比均值回归和Lasso分位数回归的评价更加准确。已有的研究已证明了弹性网约束良好的组效应性质,秩回归具有稳健性和有效性,因此如何将两者有效结合从而实现稳健变量选择是一个很有学术意义的问题。
Yang等[15]结合秩回归与SCAD罚函数提出来一种稳健的变量选择方法,但当协变量中出现复共线性情形时,效果可能会受影响,因此如何在数据出现复共线性时,研究稳健的变量选择很有意义。在已有的研究成果中,弹性网估计方面的研究都是非稳健估计,秩回归方面的研究算法几乎都是采用lars算法,且从未与弹性网估计结合进行研究。本文将秩回归与弹性网相结合进行了研究,在响应变量含有异常值或重尾分布情况下,本文所提出的估计均具稳健性和有效性,且对强相关性数据的估计效果优于Lasso惩罚秩估计、惩罚分位数回归以及最小二乘估计。在算法上对损失函数和惩罚函数采用局部二次近似,使得目标函数能求出数值解,优化其迭代算法。
1 模型简述
考虑线性回归模型:
Y=αIn+Xβ+ε
其中,Y=(Y1,Y2,…,Yn)T是n×1维响应变量,α是截距,In是元素全是1的n×1维向量,X是n×p维协方差矩阵,且不丧失一般性,假设X中心化,β是p×1维未知参数,ε是具有概率密度f(·)的独立同分布n×1维随机误差向量。假设在真实模型中,β的部分元素是零,本文的研究目标是实现零系数的识别和非零系数的稳健且有效估计。
1.1 秩回归
令ei=yi-xiTβ,i=1,2,…,n,初始估计量:
(1)
如式 (1)所示,尽管可以得到参数估计的结果,但是不能把重要的协变量选择出来。Zou等[8]提出了弹性网约束,能使部分参数压缩为零,实现变量选择。本文在式 (1)基础上加入弹性网约束。
1.2 自适应弹性网秩回归
本文提出的自适应弹性约束秩回归指用自适应弹性网惩罚秩回归模型。Zou[16]对L1惩罚部分进行加权,则惩罚函数的部分变为


(2)
式(2)称为自适应弹性约束秩回归(R-AEN)。
式(1)可以看作是Jaeckel[17]的Wilcoxon得分秩差分函数,基于文献[6],其中C(β)可有如下近似:
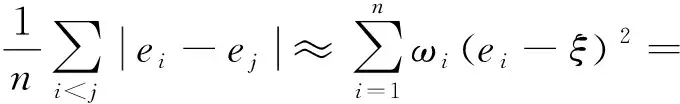

其中R(ei)是ei的秩,i=1,2,…,n。
由此,目标函数式(2)可以变成如下形式:

(3)
用局部二次近似逼近罚函数的第一部分,得

S=Y-ξIn×1
W=diag(ω1,ω2,…,ωn)
D=(S-Xβ)TW(S-Xβ) +nβTΔβ+nλ2βTβ
如式(3)所示,可以近似成如下形式:

(4)
如式(4)所示,对β求导后令其为0,得
-2XTW(S-Xβ)+2n(Δ+λ2Ip×p)β=0
则有
1.3 调节参数选择
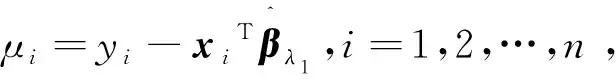

1.4 算 法
基于以上讨论,可将EN-R估计的求解算法概括为以下几个步骤:
步骤1 给定初始值βm(m=0),初始值可以由式(1)得到;
步骤2 在当前估计值β(m)下,利用β(m+1)=(XTWX+nΔ+λ2I)-1XTWS|β=β(m),得到新估计值β(m+1);
步骤3 迭代步骤2直至算法收敛。在实际操作过程中,当‖β(m+1)-β(m)‖<10-6时,停止迭代。
2 模拟和数据分析
2.1 模拟研究
在Tibshirani[1]和Fan等[18]文献中,数据来自于
yi=xiTβ+εi,i=1,2,…,n


表2 σ=0.7下各方法的模拟结果
由表1和表2可知,所提出的R-AEN估计相比其他3种方法表现更好,特别是对于厚尾(t3)或异常值(混合正态)。从模型复杂度方面看,所提出的方法NC很大,随着样本量的增加很快地接近5,NIC接近0,NCF接近1,证实了所提方法能稳健有效地识别零和非零系数。Oracle和R-AEN的MSE值很接近,并且随着样本量的增大越来越接近,说明所提方法的模型选择结果几乎接近于真实情况。随着样本量的增大,所有方法的MSE值越来越小,证明所有方法是相合估计。另外,R-AEN处理强相关变量具有更好的稳健性和显著性。综上所述,新方法能同时实现高效、稳健的模型选择,并且处理强相关性数据的能力相对更好。
2.2 中证100指数据分析
本节重点讨论R-AEN在金融市场中的应用:追踪中证100指数的表现。
指数追踪是良好的资产配置方法,该方法利用部分成分股复制目标指数的表现。此外,由于成分股与目标指数之间存在复共线性,因此本文的指数追踪用自适应弹性网秩回归方法进行研究。
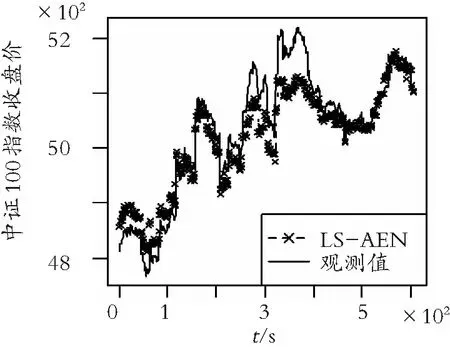
所用数据来自西南证券金点子财富管理终端,包含2020-09-28—2020-12-22的中证100指数以及所有成分股30 min线收盘价,共919个观测值,100个协变量,能有效解决中证100指数的成分股半年更新导致变量发生改变以及样本量n 分析过程中,令xij表示第j只成分股在第i次观测时的收盘价,yi表示第i次观测时的中证100指数。通常可用如下线性模型描述xij与yi之间的关系: 表3 各种方法的内预测误差(FISPE) 表4 各种方法的外预测误差(FOSPE) (a) LS-AEN方法 (b) QR-AEN方法 (c) R-L1方法 (d) R-AEN方法图1 各种方法在测试集上得到的预测值 一种估计方法FISPE和FOSPE越小,说明此方法的预测精度越高。由表3和表4知, R-AEN方法的内预测误差为611.042,明显小于其余3种方法;R-AEN方法的外预测误差为180 693.3,明显小于其余3种方法。说明R-AEN方法所选模型预测效果最佳。图1可以直观地看出: R-AEN方法值曲线与观测值曲线更接近,说明预测效果最佳,同时也说明,R-AEN方法对重要协变量的选择更加准确。 本文基于自适应弹性网和秩估计提出了稳健且有效的变量选择方法。通过数值模拟分析所得结论表明:当数据含有异常值或厚尾分布,或协变量具有强相关性时,所提R-AEN估计比现有方法更稳健和有效。本文仅从弹性网约束秩回归方面对变量选择进行了研究,关于弹性网约束秩回归中调节参数的选择还可进行研究。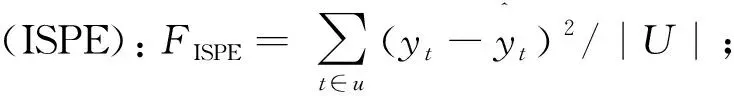





3 结 论

