水下低速密封旋转副阻力矩分析

□ 符益知 □ 陆小璐

长沙金信诺防务技术有限公司 长沙 410221

1 分析背景

由电机驱动的低速密封旋转副在水下应用时,其阻力矩会随着水压的增大而增大,从而出现在水面上测试正常,入水一定深度后电机频繁过载的现象。对此,分析水下低速密封旋转副的阻力矩,对指导工程设计与应用将具有重要的实际意义。

水下低速密封旋转副一般通过轴承定位,由电机驱动,通常采用橡胶密封圈进行密封,其阻力矩主要来源于两个方面:轴承的摩擦力矩和橡胶密封圈的摩擦力矩。轴承的摩擦力矩可以根据轴承的规格型号进行计算,橡胶密封圈的摩擦力矩计算则比较复杂。橡胶是由长链分子组成的高弹性材料,在无润滑条件下,橡胶与刚体接触面之间产生摩擦的因素主要有两方面,一方面是橡胶表面与干燥表面的黏着,另一方面是橡胶的滞后作用,摩擦力为黏着摩擦力与滞后摩擦力两者之和[1]。

黏着现象是一种表面效应,滞后现象是一种与弹性体弹性和黏弹性有关的综合现象。当橡胶被水良好地润滑时,橡胶与刚体接触面之间的黏着摩擦力将会变得很小,此时摩擦力主要为滞后摩擦力。橡胶表面和刚体相对运动时,不光滑接触面反复挤压橡胶表面,产生滞后摩擦力。当橡胶接近障碍物时,橡胶受压缩而产生能量,越过障碍物后弹性体恢复能量,假如所产生的能量完全因弹性而返回,那么不存在能量损失,摩擦力为0。在一般情况下,橡胶因分子链之间的相互作用而引起能量损失,这一损失为克服滞后摩擦力所做的功。所以,黏着摩擦力与接触面剪切阻力及接触面积有关,滞后摩擦力与接触面光滑度及橡胶材料特性有关。当接触面有润滑,且接触面积较小时,黏着摩擦力会大大减小。当接触面非常光滑,橡胶硬度较高时,滞后摩擦力也会大大减小。此外,橡胶与刚体相对滑动速度对黏着摩擦力和滞后摩擦力也有直接影响。通常速度加快时,两者都会减小。当橡胶和刚体接触面之间有润滑存在时,在一定载荷与相对运动速度下,两者接触面间会呈现弹性流体动力润滑状态,具体表现为接触面间产生一层稳定的薄膜支承,将接触面分开,摩擦力大大减小[1]。

对于水润滑橡胶轴承,在水润滑状态下,橡胶与刚体接触面间的黏着摩擦力会变得很小,摩擦主要来自滞后摩擦力[2]。在往复运动中,密封圈运动前主要表现为滞后摩擦力,可以理解为静摩擦力,运动时主要表现为黏着摩擦力,可以理解为动摩擦力[3]。对于往复运动中密封圈的黏着摩擦力,定量和通用化推导在文献[4]中给出。在这一推导中,O形圈的摩擦力分为由挤压O形圈引起的摩擦力和由压力引起的摩擦力两部分。李双喜等[5]对机械密封中的辅助O形密封圈进行有限元计算,得到接触应力和接触面积,结合试验测得的摩擦力,计算出O形密封圈的摩擦因数,结果表明在水润滑状态下,接触面形成润滑水膜,摩擦力较小。莫丽等[6]对轴用动密封Yx形密封圈进行了有限元计算,分析在往复单向动密封中的密封性能,并对不同工况下的力学性能进行研究。Bhaumik等[7]通过试验研究,对不同压力、不同往复速度下的U形密封圈的摩擦力进行测量,并分析了压力、速度的影响规律。Yang Bo[8]基于ANASYS软件对Y形密封圈、阶梯形密封圈进行了有限元分析。吴长贵等[9]利用Abaqus软件流体压力渗透载荷的加载方法对航空作动器VL密封圈进行有限元仿真分析,通过这一方法,可以自动寻找流体压力加载过程中接触与分离的临界点,提高分析精度。

笔者以水下低速密封旋转副为研究对象,推导出旋转副的摩擦阻力矩计算公式。阻力矩主要由轴承摩擦力产生的阻力矩及密封圈摩擦力产生的阻力矩组成。轴承的阻力矩根据轴承的型号计算,密封圈的阻力矩采用有限元分析得到。结合试验得到的不同压力下的摩擦阻力矩,对计算公式进行验证,同时根据计算公式对试验结果进行拟合,确定合理的摩擦因数。

2 密封圈摩擦力分析

王贤烽等[1]对橡胶尾管轴承的摩擦机理的研究表明,橡胶与刚体之间的摩擦力F为黏着摩擦力FA与滞后摩擦力FH之和,如图1所示。

(1)

式中:S为比例常数;Ai为第i个微小接触面积;n为微小接触总数。

(2)

式中:C为与橡胶类型有关的因数;Eci为橡胶第i个微小接触面积上受压缩而产生的能量;Eei为橡胶第i个微小接触面积越过障碍物后恢复的能量。

对于水下低速密封旋转副而言,其密封面圆度一般较高,且表面光滑,橡胶密封圈和结构件接触面涂抹润滑脂进行润滑。

笔者研究密封旋转副采用图2所示水下旋转试验台,旋转副活塞密封沟槽尺寸为407.54 mm,缸孔直径为420.16 mm,密封圈接触面粗糙度为1.6 μm,润滑脂采用通用航空润滑脂。采用QRAR04461-N7004星形密封圈,材料为丁腈橡胶,邵氏硬度为70。轴承采用xru21040x交叉滚子轴承,摩擦因数为0.002,旋转半径为147.5 mm。旋转副转速不高于3 r/min,密封圈线速度不高于0.066 m/s。

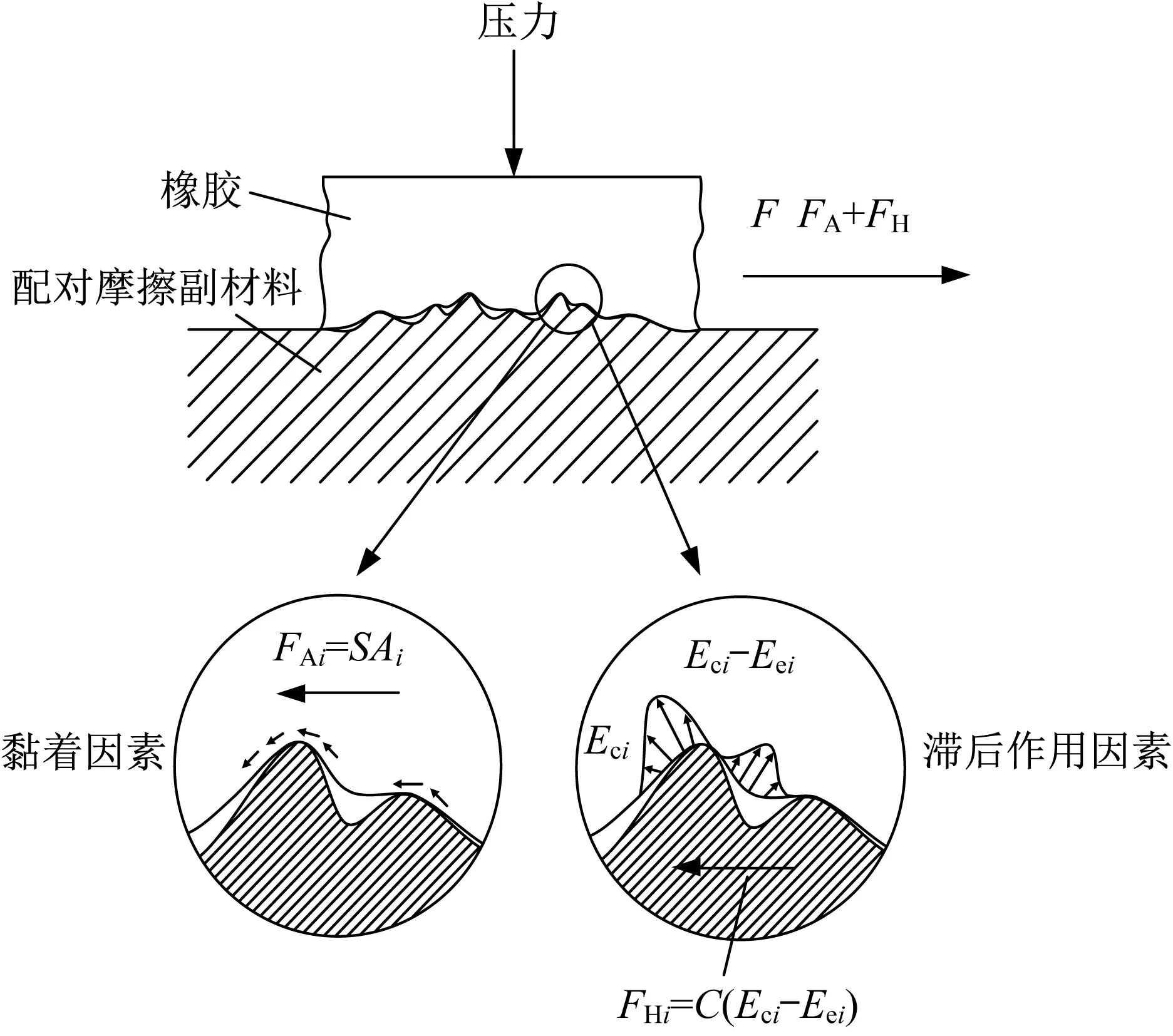
▲图1 橡胶尾管轴承摩擦机理

对于水下低速密封旋转副所采用的密封方式,摩擦力以黏着摩擦力为主,根据黏着摩擦力计算公式,令S为μσAi,其中μ为密封圈摩擦因数,σAi为第i个微小接触面积Ai的接触应力,于是有:

(3)

接触应力及接触面积都由密封圈的压缩量引起。

3 阻力矩计算

水下低速密封旋转副的摩擦阻力矩M主要为轴承的摩擦力产生的阻力矩MZ及密封圈的摩擦力产生的阻力矩MM,即:

M=MZ+MM

(4)

(5)

MM=μ∑σAiAiR0

(6)

式中:μZ为轴承摩擦因数,为0.002;R0为缸孔内径,为210.08 mm;P为密封腔内压;RZ为轴承旋转半径,为147.5 mm。

MM=RFμR02πR0/0.000 1

(7)

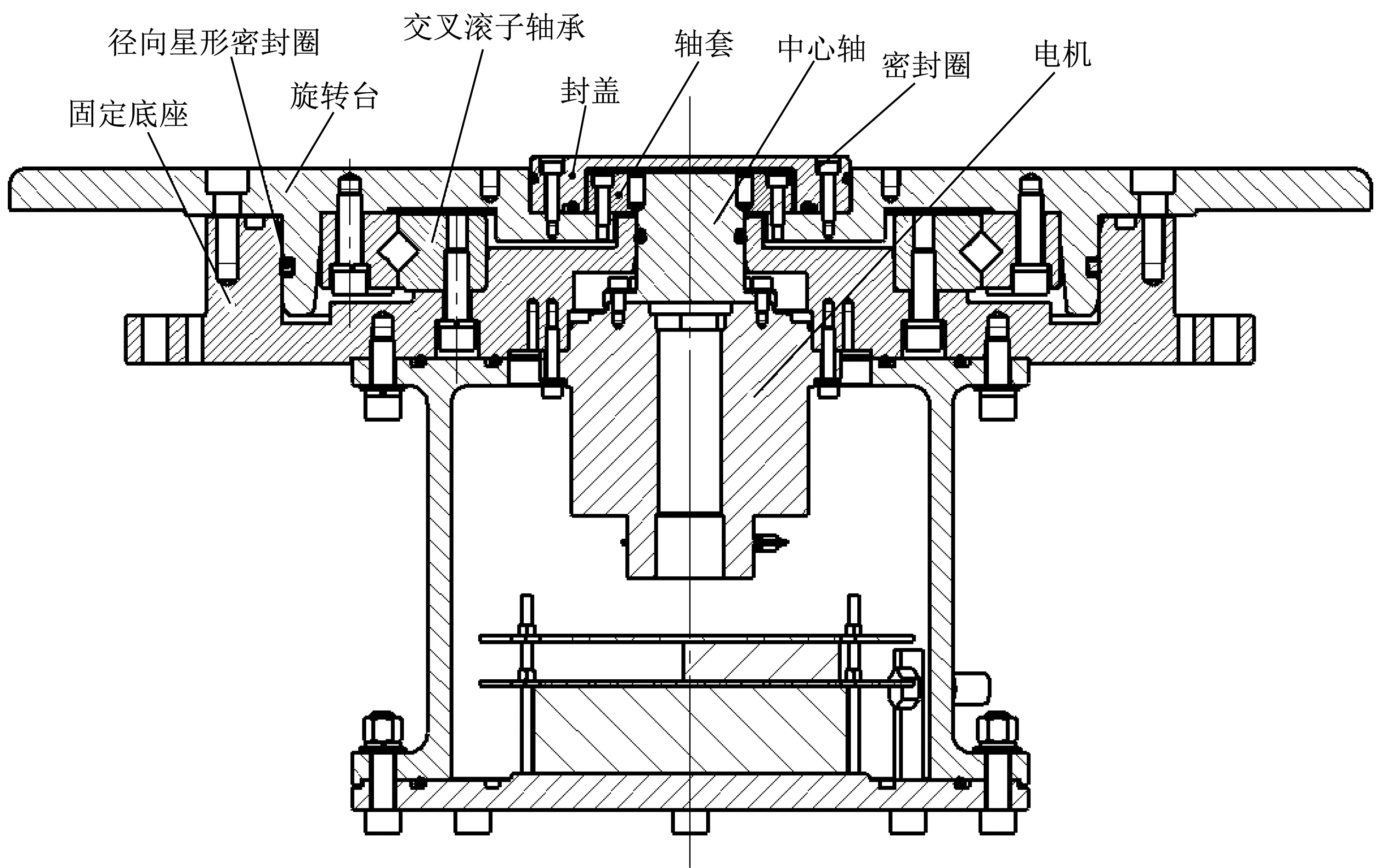
▲图2 水下旋转试验台

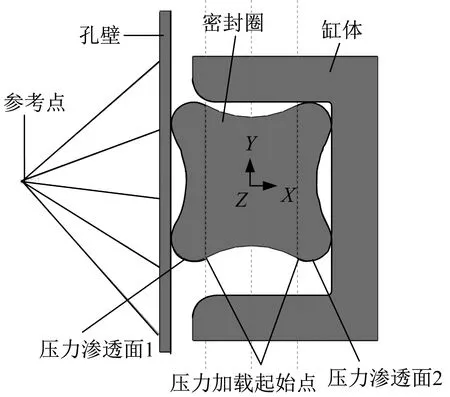
▲图3 有限元计算模型

计算不考虑结构装配产生的偏心。当转速不高于1 r/min时,摩擦热效应和弹流效应可忽略不计。中心轴密封圈旋转半径远小于径向星形密封圈半径,所以不考虑密封圈旋转产生的摩擦阻力矩。

4 橡胶材料本构模型

ABAQUS软件提供多种橡胶材料本构模型,笔者选用Mooney-Rivlin模型,正定常数C10、C01由以下公式得到[10]:

lgE=0.019 8H-0.543 2

(8)

E=6(C10+C01)

(9)

C01/C10=0.25

(10)

式中:H为材料硬度;E为弹性模量。

笔者选取的径向星形密封圈邵氏硬度为70,计算得到弹性模量为6.963 MPa,C10为0.928 MPa,C01为0.232 MPa。

5 约束与载荷

约束参考点所有自由度,约束缸体除X方向以外的其它五个自由度,约束径向星形密封圈Z方向的位移自由度。

分两步施加载荷。第一步为对缸体施加一个X方向的-0.7 mm位移载荷,模拟密封圈安装过程。第二步为对密封圈表面施加0.4 MPa压力载荷,模拟水压。Abaqus软件的Standard模块可以模拟流体穿过相互接触的两个表面,需要定义主面和从面,指定一个压力加载起始点。压力加载起始点完全暴露于流体中,流体压力将沿着压力加载起始点向接触面加载,压力加载的方向为单元法向,直到到达某个节点。这一节点的接触压力大于流体压力,此时停止加载。利用这一加载方式,可以动态找到临界点,得到更精确的计算结果。采用这一加载方式,在径向星形密封圈上定义压力渗透面1、压力渗透面2及压力加载起始点。

6 其它计算设置

分析步选择静力分析,开启非线性功能。径向星形密封圈类型采用三维二阶杂交单元。

7 计算结果

施加载荷第一步,计算结果如图4所示,此时密封压力为0 MPa。施加载荷第二步,计算结果如图5所示,此时密封压力为0.4 MPa。

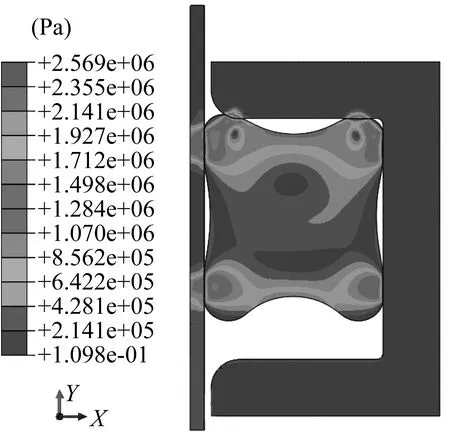
▲图5 第二步载荷计算结果

加载过程中参考点反作用力见表1,反作用力曲线如图6所示。

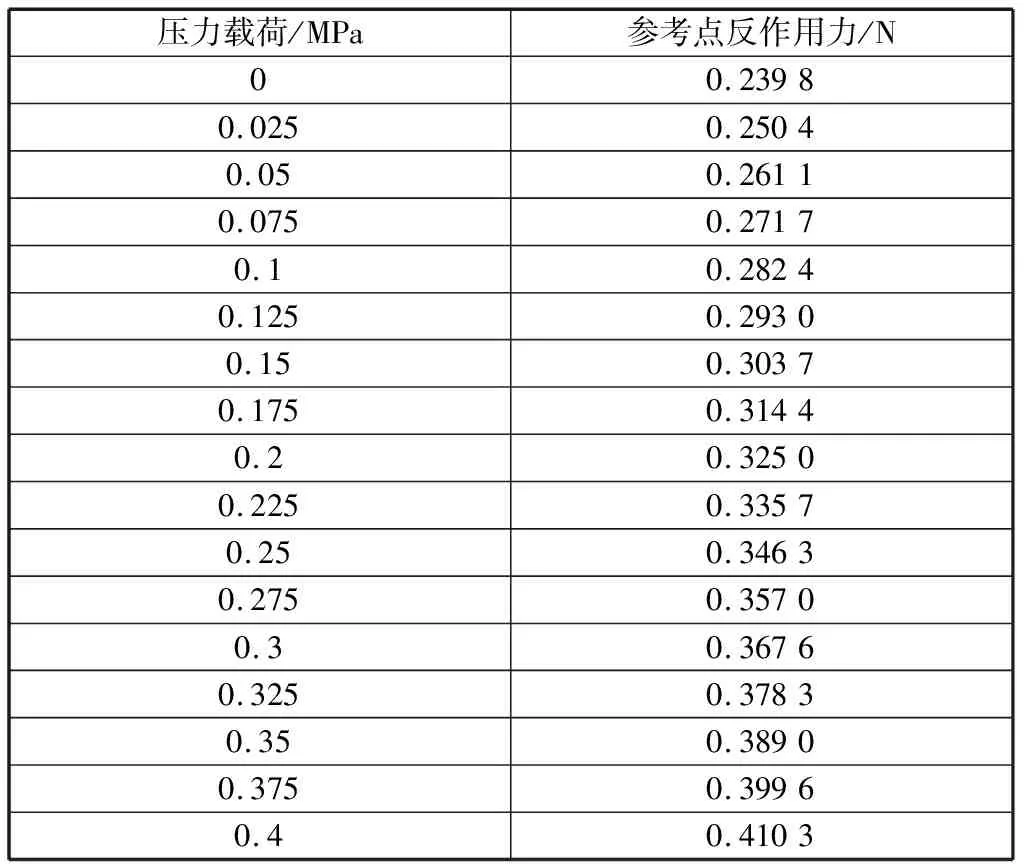
表1 参考点反作用力

0 MPa时,试验测得的摩擦阻力矩为9.4 N·m,此时轴承承受的结构重力为800 N,轴承摩擦力产生的阻力矩为0.236 N·m,则径向星形密封圈摩擦力产生的阻力矩为9.164 N·m。根据前文计算公式,计算得到径向星形密封圈的摩擦因数为0.013 8。由此可以得到摩擦阻力矩与压力的关系曲线,如图7所示。在加压前,轴承受到结构竖直向下的重力,加压后气压产生向上的推力,轴承的受力发生变化,所以在加压前段会存在一个凹点。径向星形密封圈在0 MPa时摩擦力产生的阻力矩由预压缩量决定。

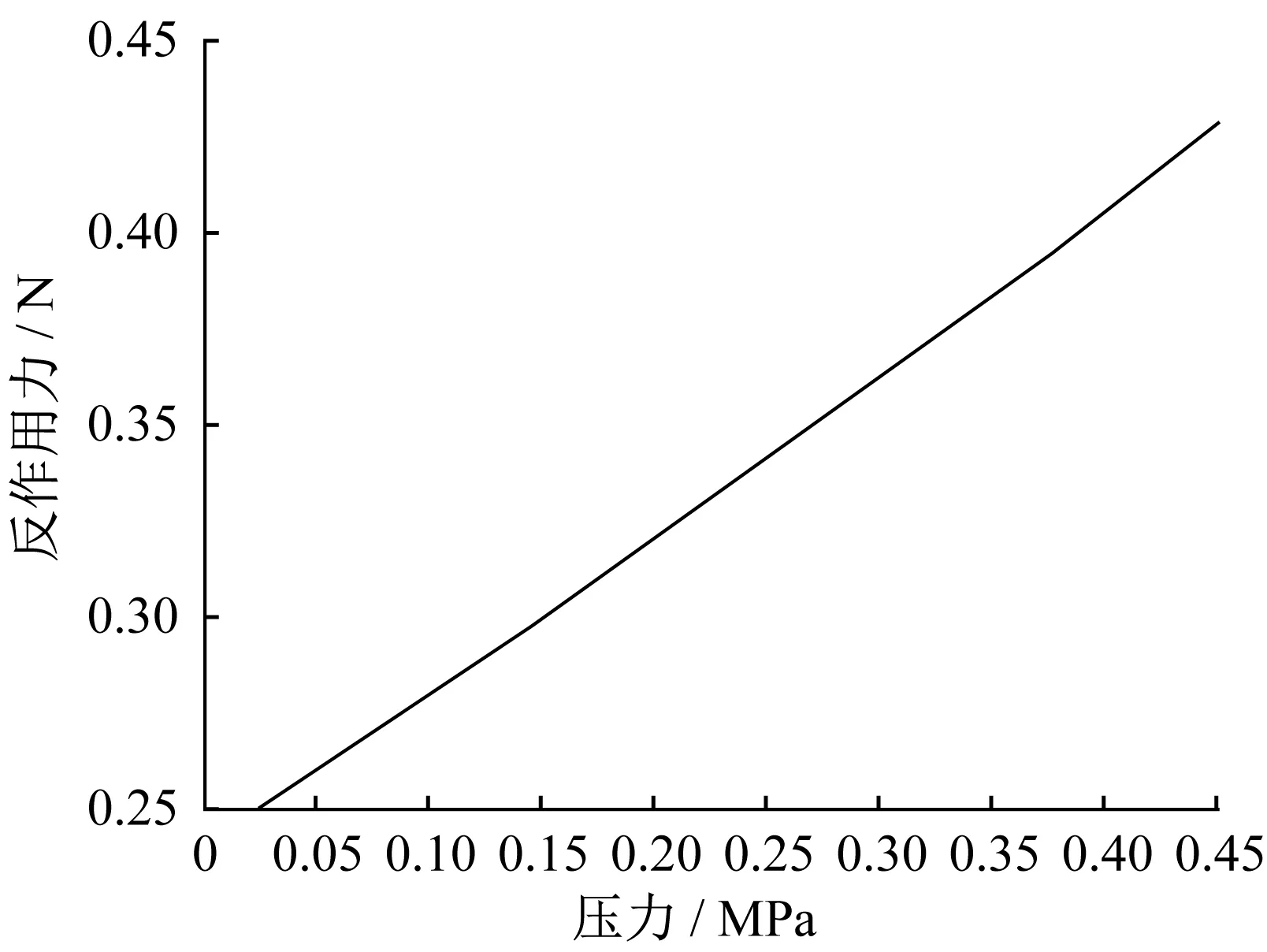
▲图6 参考点反作用力曲线

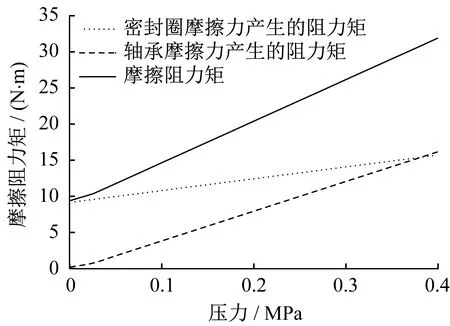
▲图7 摩擦阻力矩与压力关系曲线

由计算结果可知,摩擦阻力矩随着压力的增大基本呈线性增大。在压力小于0.382 MPa时,径向星形密封圈摩擦力产生的阻力矩大于轴承摩擦力产生的阻力矩,主要原因是径向星形密封圈会有预压缩量,初始阻力矩较大,但其增大率较小,而轴承初始阻力矩较小,承压面积远大于径向星形密封圈承压面积,增大率较大。

8 试验

水下试验成本高,并且较为复杂。由以上分析可知,水下低速密封旋转副摩擦阻力矩主要由轴承及径向星形密封圈摩擦力产生的阻力矩组成,两者都与压力有关,因此笔者对水下旋转试验台封盖进行改制,增大高度,并增加气嘴,通过气嘴向旋转腔中加气压模拟水压,固定底部结构,通过拉力计测得摩擦阻力矩。摩擦阻力矩测试如图8所示。

▲图8 摩擦阻力矩测试

试验采集五组数据,取五组数据的平均值,结果见表2。

表2 摩擦阻力矩试验结果

计算结果与试验结果基本吻合,随着压力的增大,摩擦阻力矩逐渐增大,摩擦阻力矩与压力关系曲线对比如图9所示。

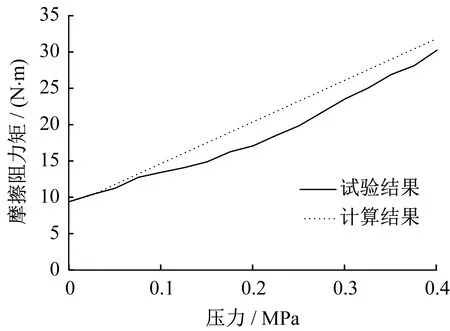
▲图9 摩擦阻力矩与压力关系曲线对比

随着压力的变化,摩擦因数也在变化,变化范围为0.010 1～0.013 8。摩擦因数随压力变化曲线如图10所示。

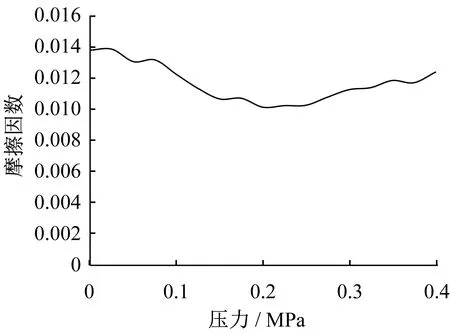
▲图10 摩擦因数随压力变化曲线

选取合适的摩擦因数,令摩擦阻力矩试验结果和计算结果的差为0,此时摩擦因数为0.011 6,对应的摩擦阻力矩与压力关系曲线与试验结果对比如图11所示。

▲图11 摩擦因数0.011 6时摩擦阻力矩与压力关系曲线与试验结果对比

由试验可知,随着压力的增大,轴承和径向星形密封圈摩擦力产生的阻力矩都将增大。密封圈有预压缩量,摩擦力产生的初始阻力矩较大,承压面积较小,所以阻力矩增大率较小。轴承摩擦力产生的初始阻力矩较小,承压面积大,所以阻力矩增大率较大。

随着压力的变化,摩擦因数也在变化,根据笔者的计算模型,摩擦因数取0.011 6较为合理。

9 结束语

通过对比理论计算结果与试验结果,笔者采用的水下低速密封旋转副阻力矩计算方法的有效性得到了验证,有助于工程设计。