大空间建筑下送风分层空调系统区域间换热特性研究

王海东 胡 浩 朱杰克 杨昕琦 王瑞鲲

(1 上海理工大学环境与建筑学院 上海 200093；2 航天万源实业有限公司 北京 100071)

大空间建筑中，人员活动区域的高度远低于建筑内部高度，为降低空调能耗，夏季普遍采用分层空调来营造室内热环境，保证建筑下部人员活动区域(空调区)热舒适性，而建筑上部区域(非空调区)不进行空气调节[1]。与全室空调相比，分层空调可显著减少室内冷负荷、降低系统运行成本[2]。但大空间建筑垂直方向上温度梯度较大，屋顶聚集了大量热，合理利用屋顶排风排出此部分热量，能有效减少非空调区向空调区所产生的对流转移热和辐射转移热[3]。

非空调区向空调区转移的辐射换热量和对流换热量是分层空调负荷计算的关键[4-5]。辐射换热量可通过实验获取各壁面温度进而求得，而对流换热量难以通过实验直接测得。上下区域间的对流换热量包括气流换热量和温差导热量两部分。其中，气流换热量可以通过分层面处的气流质量流量计算得到，而准确计算温差换热量则难度较大。S. Togari等[6]提出一种温度基准区域模型来预测大空间建筑能耗和室内热环境，实验得到经验系数Cb=2.3 W/(m2·℃)来估算大空间建筑分层面上的温差导热量。Cb被定义为区域间传热系数，是指单位面积单位温差下通过空气层的热交换量，不包括空气质量交换产生的热交换量。但经验值2.3 W/(m2·℃)并不能完全适用于所有大空间建筑分层面上热量计算，如在DOE-2软件中Cb被设定为14.8 W/(m2·℃)[7]，而在某中庭空间的温度分层模型中取10 W/(m2·℃)[8]。目前不同研究给出的Cb差异较大，因为它取决于特定的室内空气流动特性。Gao Jun等[9]从理论上得出Cb与气流湍流状况直接相关的结论，明确了该系数的物理意义，并建立了数值解析方法。Wang Haidong等[10]通过实验分析和数值模拟研究了带有侧壁喷口送风系统的大空间建筑中层间热转移，指出Cb取值受局部湍流强度的影响。

目前，大空间建筑室内热环境和气流组织的研究主要针对喷口送风的气流组织形式[10-13]，柱状下送风分层空调近年来才逐步推广。本文采用实验和CFD相结合的方法，旨在研究排风作用下的大空间建筑下送风分层空调系统区域间换热情况和负荷特性，重点研究了室内垂直温度分布、冷负荷预测及区域间传热系数Cb的取值。缩尺模型实验旨在保证 CFD模拟的准确性，将验证过的缩尺数值模型通过相似理论拓展至全尺寸工况模拟，以反映实际大空间建筑室内热环境，为下送风分层空调负荷计算提供理论指导。

1 研究方案

1.1 实验研究

为研究大空间建筑下送中回气流组织下的分层空调室内热环境和区域间换热特性，本文采用带有柱状送风口的缩尺模型实验室，实验室内部场景如图1所示。该实验室是以实际的大空间建筑为原型，按照几何比例1∶4搭建而成。实验室呈坡屋顶结构，落地布置6个半圆柱状送风口，实验系统及尺寸如图2所示。柱状送风口直径为0.16 m，高度为0.41 m。距地1.1 m处布置圆形回风口，其直径为 0.4 m。对于大空间热环境和分层空调冷负荷而言，排风比是一个关键影响因素，计算方法为系统的排风量与送风量之比。因此本研究以排风比为实验变量，设计了3个工况的对照实验。排风口设置在屋顶，每个工况均设置4个功率为40 W白炽灯，实验方案如表1所示。实验室墙面和屋顶贴有均匀发热的热电膜，模拟稳态条件下的围护结构得热，地面有0.1 m的保温层以防止热量散失。

图1 缩尺实验室内部场景

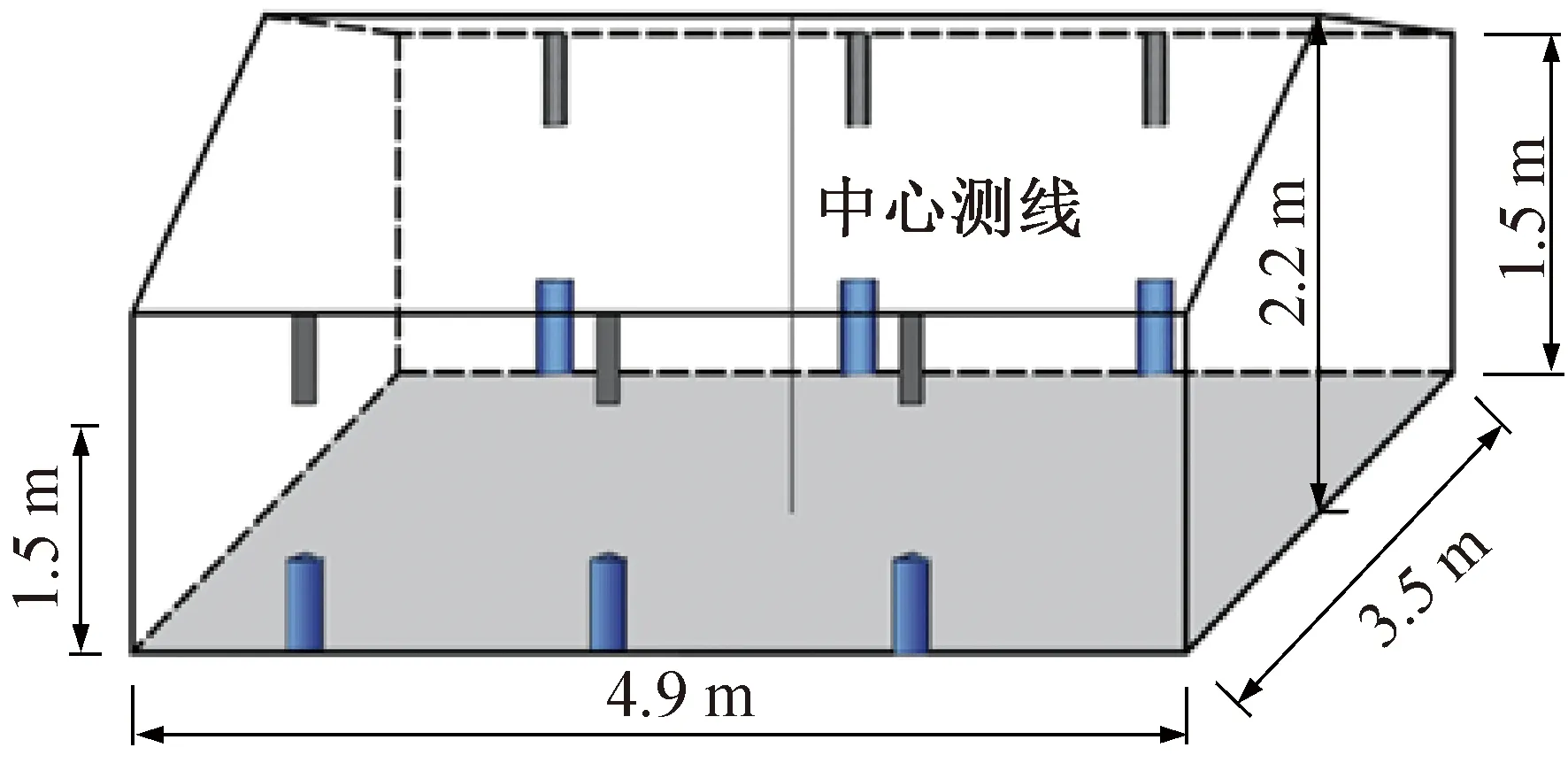
图2 缩尺实验室尺寸

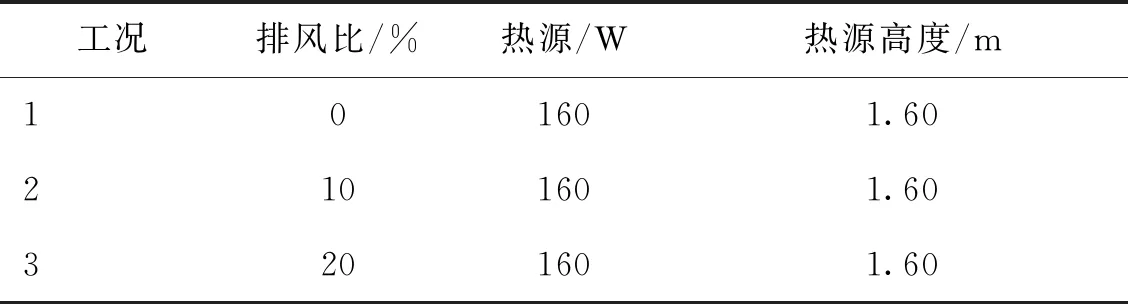
表1 实验工况设置

室内中心位置布置一条垂直温度测量线，空气温度采用Tsic506温度测点(测量范围：-10～60 ℃，分辨率：0.01 ℃，精度：±0.1 ℃)进行测试，线上共有测点22个，间距为100 mm。送风、回风、排风的温度和速度均采用SWA-300热线风速仪(测量范围：0.1～30 m/s，分辨率：0.1 m/s，精度：±3%读数)在送风主管处进行测试，经过圆管内速度修正后可得到实验的送风量和平均送风温度。屋顶和壁面热流密度采用JTNT-A建通热流密度计(测量范围：0～2 000 W/m2，分辨率：0.1 W/m2，精度：±3%读数)和HFP01热流密度计(测量范围：-2 000～2 000 W/m2，分辨率：0.1 W/m2，精度：±5%读数)进行测量，测点布置如图3所示。Testo 512 压差测量仪(测量范围：0～2 000 Pa，分辨率：0.1 Pa，精度：±0.5%全量程)测量室内外压差，保证风量平衡。

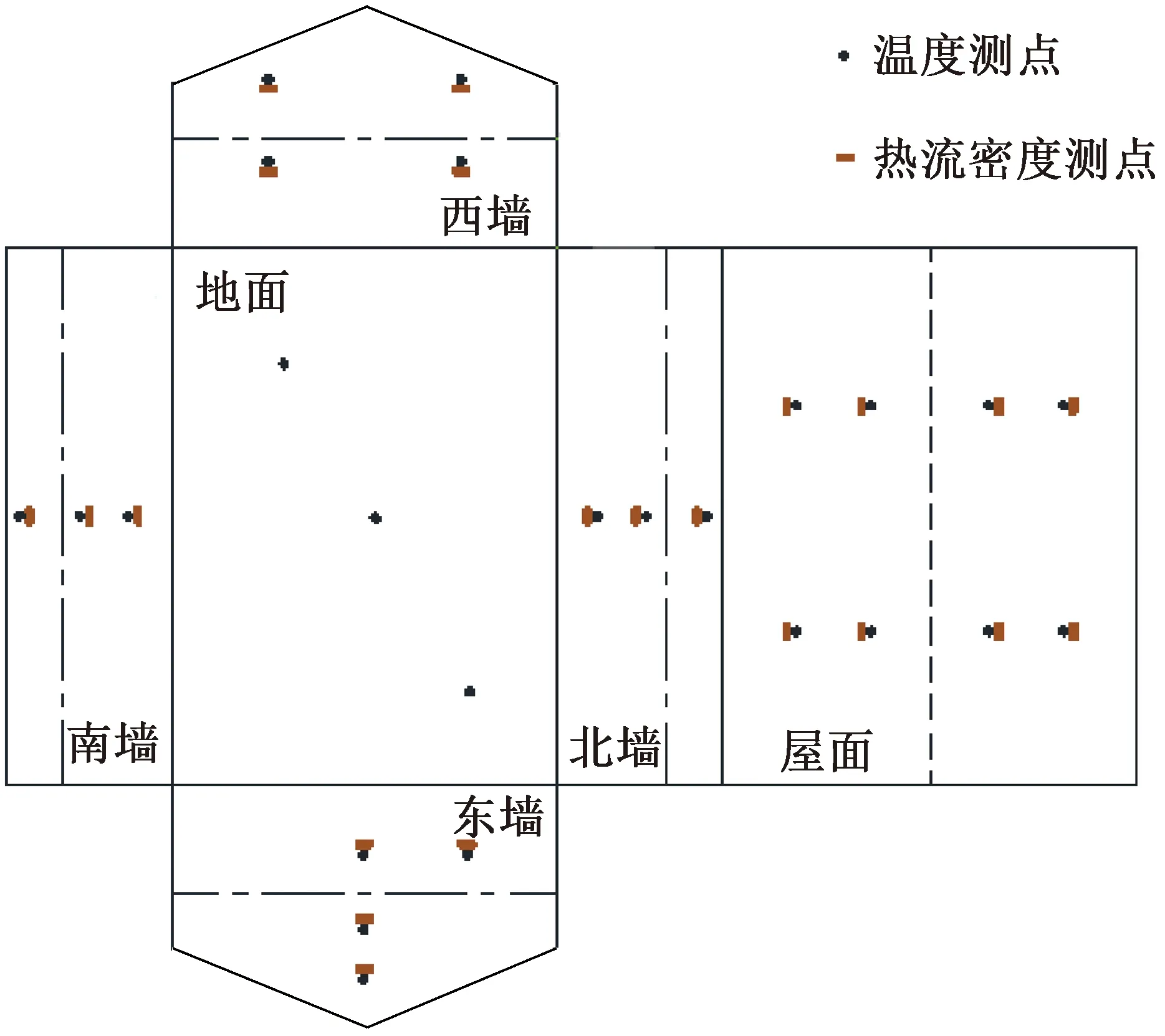
图3 温度和热流密度测点布置

1.2 相似理论

对室内热环境而言，模型与原型达到温度场相似是主要目的。C. Walker等[14]分析室内气流的控制方程后，尝试将雷诺数(Re)、阿基米德数(Ar)和普朗特数(Pr)作为获得原型和模型之间相似性的3个准则数。其中，Pr表征流体物性对传热的影响，缩尺模型与原型采用同种介质，满足Pr相等。当空气作为介质流体时，原型与模型的Re和Ar不能同时满足相等[15]。

大空间建筑垂直方向上温度梯度显著，导致空气密度不相等，此时空气流动主要由于重力和浮升力的不平衡引起，因此将Ar作为主要准则数，使其在原型和模型中相等，Re只需保证进入紊流自模区。当模型风口Re>2 400时，即运动状态处于紊流自模区，可近似认为与Re无关[16]。如表2所示，缩尺模型风口处的空气雷诺数大于2 400，全尺模型风口处的雷诺数为缩尺模型的8倍。说明两种尺度模型中气流均处于紊流自模区。

表2 缩尺模型与全尺模型送风口处雷诺数

(1)

(2)

(3)

式中：ρ为流体密度，kg/m3；v为流体流动速度，m/s；L为特征长度，m；μ为流体动力黏度，N·s/m2；g为重力加速度，m/s2；ΔT为送风气流与室内空气的温差，℃；Ts为送风温度，℃;cp为空气比热容，J/(kg·℃)；λ为空气导热系数，W/(m·℃)。

考虑到室内空气的热交换，根据通风排热能量方程：

Q=ρvcpFT

(4)

式中：F为送风口面积，m2。

将Q带入Ar中，可引出热量阿基米德数ArQ：

(5)

通过相似条件的转换，式(2)和式(5)可分别表示为：

(6)

(7)

将送风温度比例尺CTs和温差比例尺CΔT定为1，相应的其他比例尺如表3所示。

表3 参数相似比例尺

1.3 CFD模拟研究

本文模拟采用广泛用于建筑室内热环境和气流组织模拟的CFD软件PHOENICS。根据实验室尺寸，建立了缩尺数值模型，房间送风、回风、排风口面积和实验室保持一致。全尺模型根据缩尺实验室尺寸以4∶1的比例进行建模。在温度梯度和速度梯度较大的区域，如壁面、屋顶、地面及风口等，对网格进行加密处理，以保证计算的精度。经网格无关解检验后，最终选取60万网格数。压力-速度耦合采用SIMPLEST算法，湍流模型采用标准k-ω模型，辐射模型采用IMMERSOL模型。通过5 000次的迭代计算后，计算残差曲线趋于稳定，可认为模拟已达到平衡状态。

本文研究稳态工况，实验和数值模拟壁面的热量均为恒定值。在缩尺数值模型中，根据实验测得数据设置墙和屋顶的热流密度值；全尺模型的边界条件是根据缩尺工况以及相似比例尺确定。墙、屋顶、地面发射率取为0.93。对于无排风的工况，回风口边界条件采用压力出口，排风口设置为壁面；对于有排风的工况，回风口采用速度出口，排风口采用压力出口。各工况边界条件设置如表4所示。

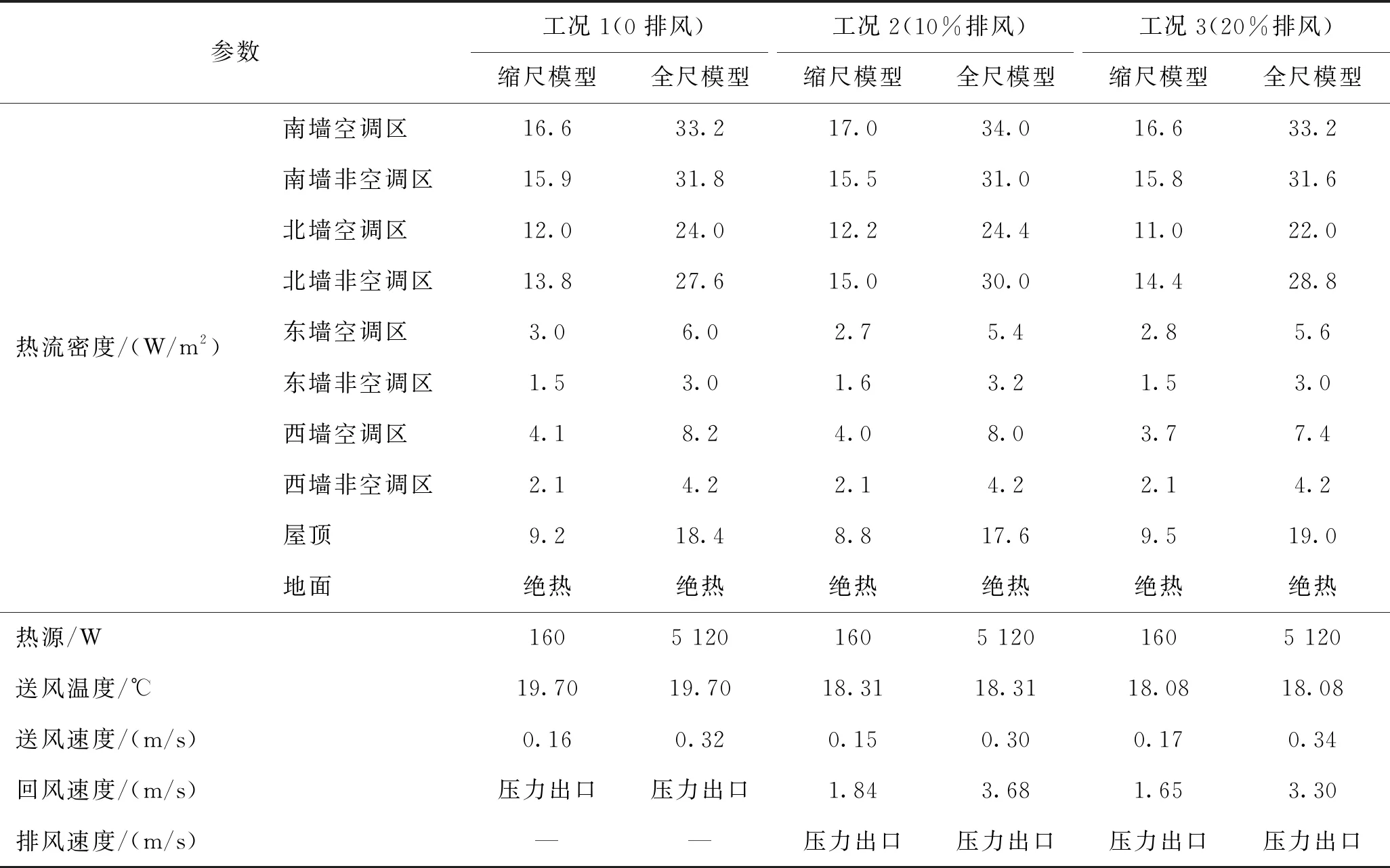
表4 CFD边界条件设置

2 CFD结果验证

2.1 中心线垂直温度验证

针对3个不同排风比工况，采用中心线温度分布来验证室内热环境模拟的准确性。垂直温度分布验证如图4所示，在两种送风系统缩尺模型下，实验和数值模拟得到中心测线温度分布基本一致，说明数值模拟结果可以较好的反映室内热环境。将验证过的缩尺模型按几何比例尺CL=4放大为全尺模型进行数值计算，得到全尺模型的中心线温度分布，可以看出缩尺模型与全尺模型的室内热环境相似。此外，通过实验数据分析可得，非空调区的温度梯度随着排风比增加而减小，说明屋顶排风可以有效降低非空调区的空气温度和热量积聚。

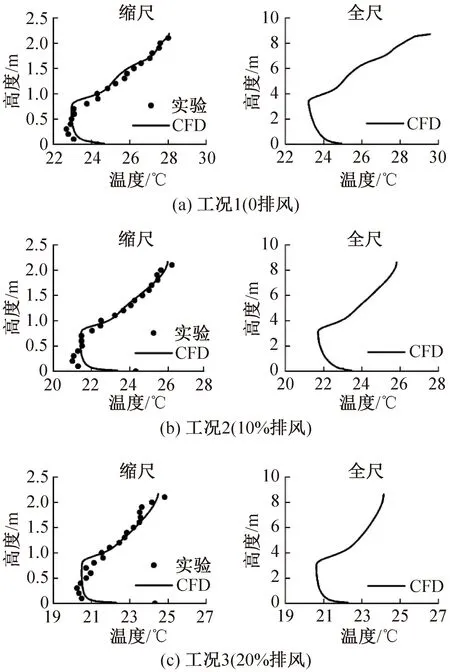
图4 垂直温度分布验证

2.2 夏季空调冷负荷验证

除了温度分布情况以外，空调冷负荷也是本文研究的重点。从系统能量平衡的角度，整个空间的冷负荷Qtotal可根据式(8)计算：

(8)

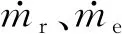
若以空调区为研究对象，在稳态条件下，空调区的冷负荷Qc由式(9)计算：

(9)

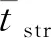
稳态模拟工况下，由于不考虑各壁面负荷延迟和衰减作用，因此认为得热即为负荷，可计算出围护结构负荷和辐射转移负荷。空调区围护结构得热Qenv可通过实验数据获得，并作为CFD的边界条件输入。采用Gebhart 辐射模型[17]计算非空调区各壁面向空调区辐射热量之和，即辐射转移负荷Qrad；根据热量平衡关系，非空调区向空调区的对流转移负荷Qmig为：

Qmig=Qc-Qenv-Qrad

(10)

表5所示为基于缩尺模型的实验与CFD模拟得到的冷负荷对比。由表5可知，三种不同排风比的工况下，实验和CFD得到的空调区冷负荷的误差分别为1.35%、-2.75%、0.52%。因此CFD数值模拟能较好的反映实验结果，验证后的数值模型可用于全尺工况扩展。

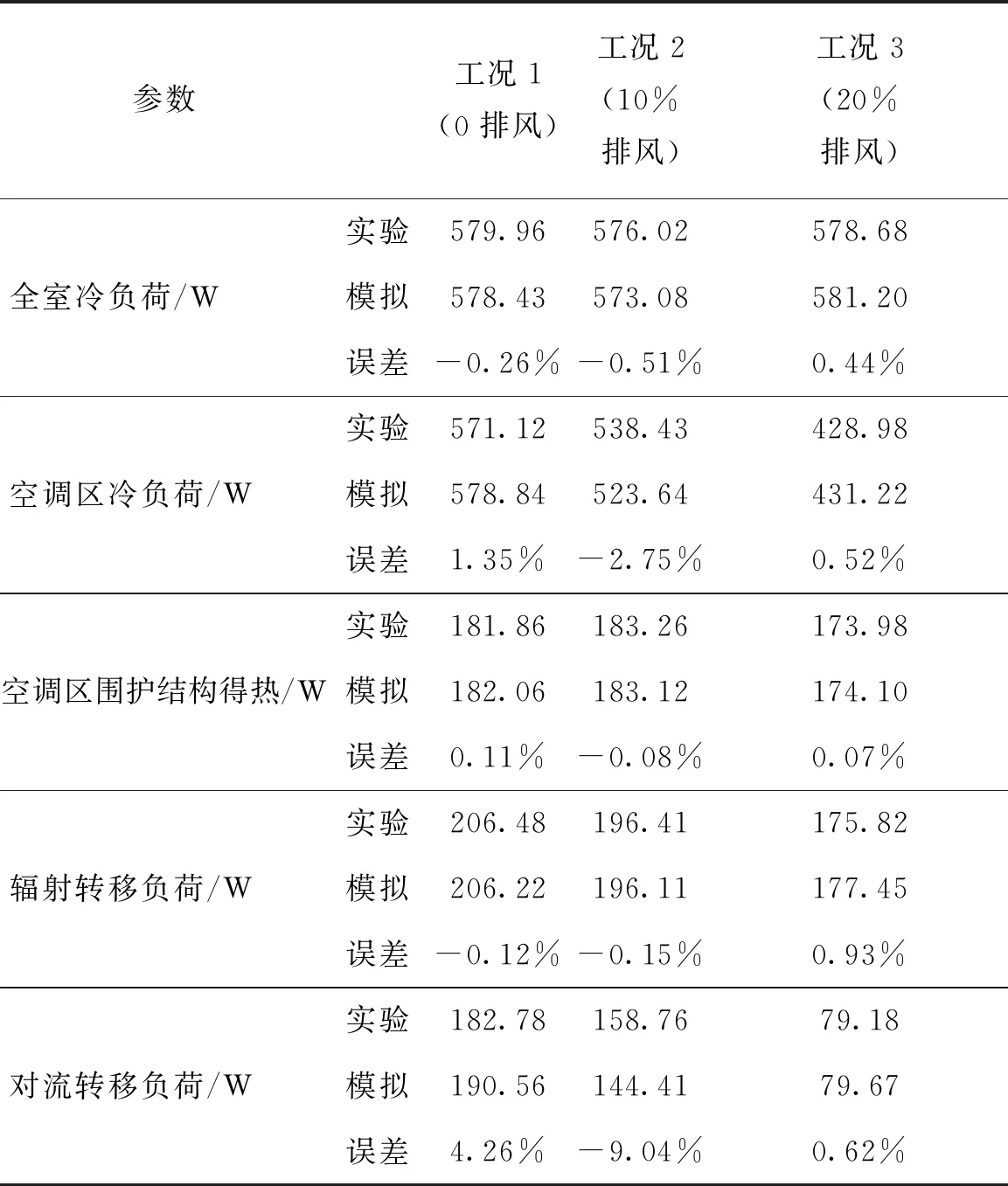
表5 基于缩尺模型的实验与CFD模拟得到的冷负荷对比

3 结果分析

3.1 对流转移热分析

从传热机理角度分析，分层界面上的对流转移热Qmig一部分是由于气体质量流量引起的气流换热量Qconv，另一部分是由于温差引起的导热量Qcond。因此，Qmig可由式(11)计算：

Qmig=Qconv+Qcond

(11)

3.1.1 气流换热量Qconv

对于CFD数值模型，可认为分层面处布满一层细密网格，该层网格的每个微元均可能产生向上或向下的速度，为排除这种空气额外流动造成的影响，采用加权温差来计算气流换热量，如式(12)：

(12)

式中：ωi为第i个节点垂直速度分量，m/s；Ai为第i个网格面积，m2;ti为第i个节点空气温度，℃。

3.1.2 温差导热量Qcond

气体间的导热有别于固体，除了气体本身的导热系数外，还受到湍流的影响。每个网格节点i的湍流空气导热系数λi的计算式为[10]：

(13)

式中：μt为空气湍流动力黏度，Pa·s；Prt为湍流普朗特数。

根据傅里叶定律，温差导热量的计算：

(14)

式中：δ为网格厚度，m。

基于两种尺度的数值模拟结果如表6所示，所有工况对流转移热的计算误差均在10%以内，说明了CFD方法的可靠性。全尺模型数值模拟得到的转移热平均约为缩尺工况的32倍，验证了前文相似尺度的正确性。对于柱状下送风系统，对流转移热中由温差引起的热传导占主导作用，且随着屋顶排风量的增加，温差导热量降低。

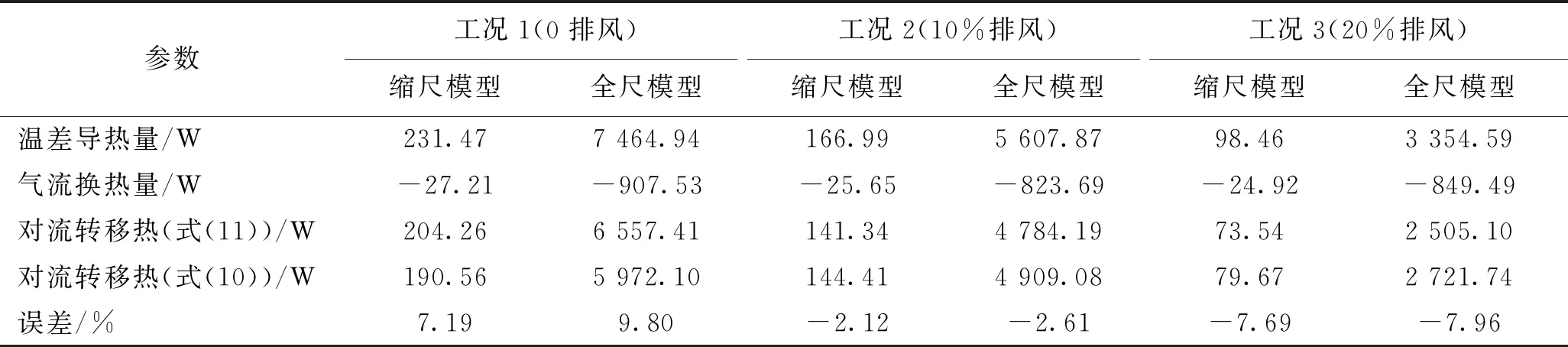
表6 基于微观法和热平衡法得到的区域间转移热

3.2 区域间传热系数

区域间传热系数Cb的定义为单位面积单位温差下通过空气层的导热量，与气流换热量无关。图5所示为基于网格节点求解Cb原理，提出了一种基于网格节点的微观分析方法，分层面上各个微元温差传热系数Cbi由式(15)计算。由分层面总温差导热量和相邻区域特征温差可得到区域间传热系数Cb，如式(16)所示。通过计算分界面上每个网格节点湍流空气导热系数λi的算术平均值，即可获得分层面处湍流导热系数λt。

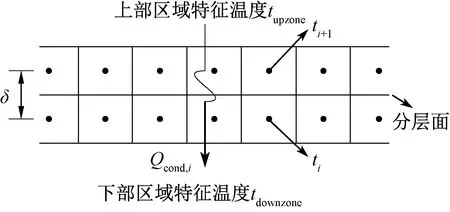
图5 基于网格节点求解Cb原理

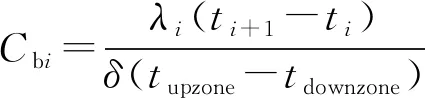
(15)

(16)

式中：A为分层面总面积，m2；tupzone、tdownzone分别为上部区域、下部区域的特征温度，℃。

3.2.1 二区域划分下的结果对比

基于全尺模型模拟结果，选取垂直方向4.5 m处(略高于回风口)截面作为分层面。表7所示为二区域划分下区域间传热系数Cb和湍流导热系数λt。由表7可知，全尺模型的Cb约为缩尺工况下的2倍。当屋顶无排风时，分层面处Cb较大；随着排风比的增加，Cb取值有所降低。缩尺模型下，Cb接近经验值2.3 W/(m2·℃)[6]。而全尺模型得到的Cb与2.3 W/(m2·℃)相差较大,表明以往的对流转移负荷计算低估了温差换热量。

表7 二区域划分下区域间传热系数和湍流导热系数

相同的缩尺模型实验室，Wang Haidong等[10]计算了侧壁喷口送风系统的区域间传热系数，1.05 m分层面(略高于喷口所在截面)平均Cb约为12 W/(m2·℃)，本文研究的缩尺工况分层面平均Cb在1.78～3.92 W/(m2·℃)之间。这种量级差异是因喷嘴射流引起较强的湍流，Cb与湍流黏度密切相关。表明气流组织形式影响区域间传热系数取值。

3.2.2 四区域划分下的结果对比

考虑到送、回风口和坡屋顶的影响，在全尺工况二区域划分下，进一步在垂直方向2、6 m高度将整个空间划分为4个区域，计算不同截面区域间传热系数值和湍流导热系数，结果如表8所示。以工况1全尺模型为例，Cbi分布云图如图6所示。

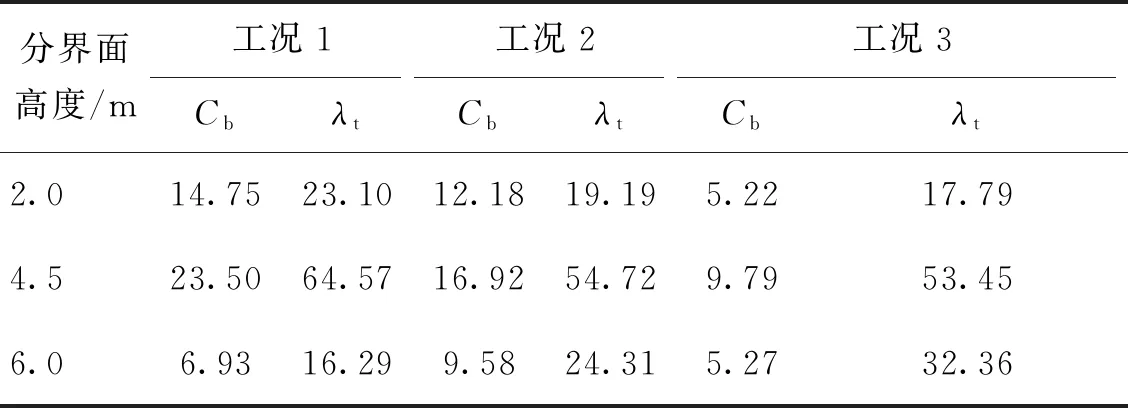
表8 四区域划分下得到的Cb(W/(m2·℃))和λt(W/(m·℃))(基于全尺模拟)

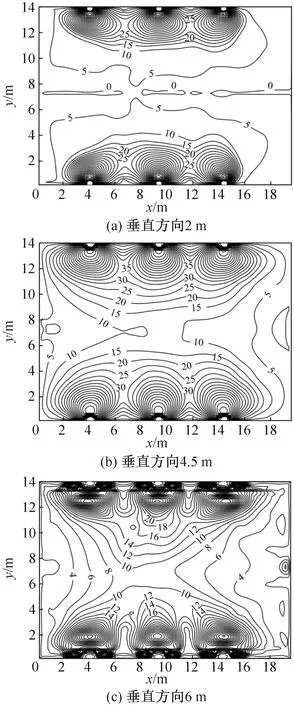
图6 工况1四区域划分下Cbi(W/(m2·℃))分布云图

不同高度的分界面上，Cb存在较大差距。在垂直方向2 m处，送风口附近区域湍流波动剧烈，垂直方向温差较大，而远离送风口的气流相对稳定，所以送风口附近的区域间传热系数较大，距离送风口较远区域间传热系数较小。在4.5 m高度处，由于回风口抽吸作用，使空调区和非空调区的空气相混合，造成分层面上下空气层温差较小，湍流导热系数较大，因此Cb较大。随着高度增加，空调区和非空调区空气混合减弱，虽然非空调区垂直空气温度梯度较大，但气流相对均匀，并未产生剧烈扰动，所以Cb较小。由此表明Cb受气流状态的影响。

表9所示不同区域划分方式下分层面垂直方向4.5 m处Cb对比。对于不同区域划分方式，在垂直方向4.5 m分层面上，二区域划分和四区域划分所计算得到的Cb存在差异。由此可知，区域划分方式也会影响Cb的取值。但区域划分方式的影响远小于气流状态的影响，但大于屋顶排风的影响。

表9 不同区域划分方式下分层面垂直方向4.5 m处Cb(W/(m2·℃))对比(基于全尺模拟)

4 结论

本文以大空间缩尺模型实验台为基础，进行了变排风比的热环境实验。根据实验得到的中心线垂直温度分布和空调冷负荷结果，证实了CFD数值模拟能够准确反映室内热环境和负荷特性。基于相似理论，进一步将缩尺工况拓展到全尺寸模拟研究，得到结论如下：

1)不同工况下，热平衡法和微观法得到的对流转移热的相对误差均在10%以内，验证了微观法的可靠性。微观法的提出克服了热平衡法对于空调负荷和辐射转移负荷的高度依赖性。

2)在柱状下送风系统中，由温度梯度引起的热传导在区域间对流转移热中占据主导地位。

3)以分层面为基准(原型建筑为4.5 m处)将整个室内空间分割为上下两个区域(二区域划分)，原型建筑的区域间传热系数Cb在排风比为0、10%、20%时分别为7.92、6.14、3.81 W/(m2·℃)。

4)区域间传热系数Cb取值受到气流状态、区域划分方式和气流组织形式的影响，而受屋顶排风的影响较小。