适应自动换刀功能的超声电主轴结构设计及实验研究

刘建慧,马志鹏，郭星辰

(河南理工大学 机械与动力工程学院，河南 焦作 454000)

0 引 言

由于切削力小、切削热少、刀具耐用度高、加工稳定、生产效率高，超声切削技术被广泛应用于硬脆材料、蜂窝材料和航空航天材料等难加工材料的加工。超声切削技术与普通机床有机融合形成具备超声功能的机床是实现超声加工的基础。由于加工中心的诸多优势及其应用普及，超声加工中心的开发成为必然趋势，而超声主轴是其中最重要的功能部件。目前常见的超声加工装置通过换能器、变幅杆、电能无线传输装置与标准刀柄锥部组合为超声刀柄，进而安装到机床主轴进行加工[1],这种结构的超声刀柄自身能获得较好的振动和加工效果。但由于主轴和超声加工装置单独设计，超声刀柄的尺寸大、重量大，相当于增大了主轴的悬伸量，导致主轴刚度和抗振性能下降，而且不利于自动换刀。另外，超声刀柄的振动必定会影响主轴轴承的旋转精度和寿命，从而降低了主轴整体的转动精度和寿命。

针对以上问题，国内外学者设计了多种新型的超声加工装置。李征等[2]用有限元分析方法设计优化了整体式超声振动内圆磨头主轴系统，分析了变幅杆套筒尺寸对轴承安装位振幅的影响，避免了超声振动对轴承的影响；马中秋[3]设计了一种可自动更换超声装置的超声波切割主轴及自动更换设备，该主轴可以对整个超声装置进行整体更换，保证不同工具都能有稳定的振动；S.Kobayashi等[4]设计制作了超声振动辅助电化学加工电主轴，将变幅杆内置到电主轴内腔，结合电化学加工，取得了较好的加工效果；S.N.Shatokhin等[5]，A.O.Golovin等[6]设计制作了基于静压轴承的超声振动主轴，并利用油压传递振动，消除了采用碳刷铜环进行电能传输带来的不利影响。

有限元分析软件可以对已设计的结构进行校核。顾荣华等[7]对变幅杆进行了动力学分析，结果与解析值相吻合；秦然等[8]采用实验对转子临界转速的解析法和模态分析法进行验证，证明模态分析法求解速度快，准确性高，为工程应用提供了依据。

目前市面上比较成熟的超声加工机床有德马吉的Ultrasonic系列加工中心，该加工中心电主轴具有电能无线传输功能，配合自研的超声刀柄和针对该刀柄的专用刀库和换刀机械手，实现超声加工的自动换刀功能。但该加工中心整机价格昂贵，并且互换性差，无法配合其他标准化产品使用。其他相关产品同样存在标准化程度低，难以实现自动换刀等问题。为此，本文提出一种基于HSK标准刀柄、适应加工中心自动换刀功能的超声加工电主轴，并对其主要结构进行设计、仿真分析和功能实验。

1 超声加工电主轴的结构设计

1.1 电主轴主要结构

超声加工电主轴主要结构图如图1所示，主要由变幅杆、换能器、主轴、拉刀装置(未在图中显示)、无壳电机、电能无线传输装置等部分组成。其中，HSK刀柄与变幅杆1共同组成一个半波长变幅杆，将换能器2产生的超声振动进行放大。超声电能由主轴尾部的无线传输装置传输[9]，避免高速旋转过程中碳刷产生打火现象。HSK刀柄通过拉刀机构安装在主轴上。电主轴配合打刀缸、换刀机械手和刀库实现自动换刀。

1.2 变幅杆设计的四端网络法

四端网络由两个输入端、两个输出端及多个元件组成，各元件均是双向、线性和无源的，其结构如图2所示。

1-变幅杆；2-换能器；3-主轴；4-电机转子；5-电机定子；6-电能无线传输装置。

图2 四端网络Fig.2 Four-end network

任一四端网络的输入端、输出端及各参数之间的关系用如下传输方程表示：

(1)

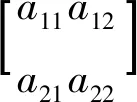
1.3 复合超声变幅杆的设计计算

图3为复合变幅杆的结构图。该结构以HSK32-E型刀柄作为变幅杆小端，以圆柱端作为大端，并用圆锥段相连接。

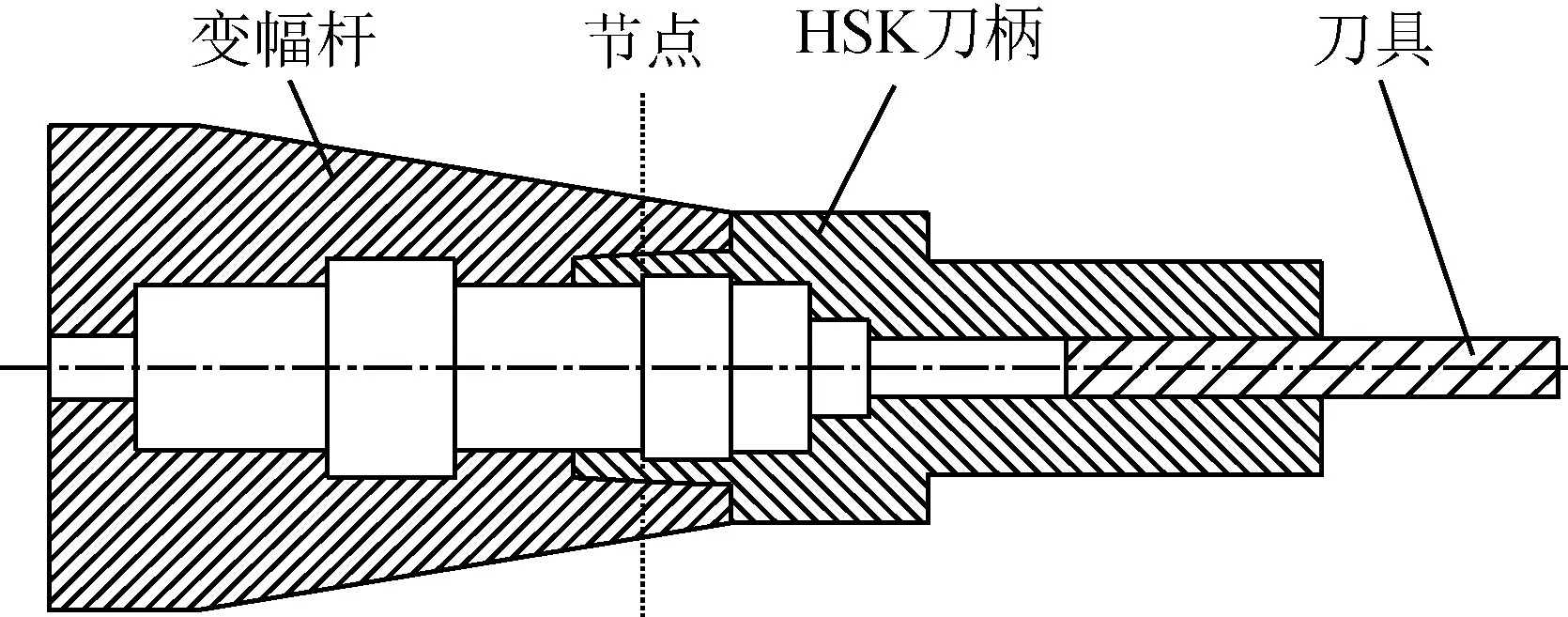
图3 复合超声变幅杆结构图Fig.3 Structure diagram of composite ultrasonic horn

变幅杆内孔用于安装拉杆和拉爪。为便于计算和仿真分析，忽略微小结构，并将刀具简化为一段均匀圆柱体。

将复合超声变幅杆从各截面变化处分为12段单一形状变幅杆，依据变幅杆各段连接面位移和力传递的连续性，将各单一形状变幅杆的等效四端网络首尾连接，构成复合超声变幅杆的等效四端网络,如图4所示。

图4 复合超声变幅杆四端网络Fig.4 Four-end networks of composite ultrasonic horn

根据任意均匀细长杆的谐振方程，可求得各段传输方程如下[11]：

(1)第n段为带圆柱孔的圆柱杆时，

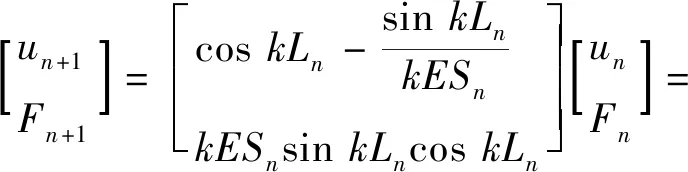
(2)

式中：k为圆波数，k=ω/c=2πf/c；f为谐振频率；Ln为第n段长度；E为材料弹性模量；Sn=π(Rn12-Rn32)，Rn1为等截面杆外圆半径，Rn3为等截面杆内孔半径；An为第n段传输矩阵。

(2)第m段为带圆柱孔的圆锥杆时，

(3)

式中:Lm为第m段长度；Rm1为第m段大端外圆半径；Rm2为第m段小端外圆半径；Rm3为第m段中心孔半径；Sm1=π(Rm12-Rm32)为第m段大端截面面积；Sm2=π(Rm22-Rm32)为第m段小端截面面积；Am为m段传输矩阵。

根据图4所示网络，联立式(2)～(3)可得变幅杆的总传输方程为

(4)

式中，Aα=A12A11A10A9A8A7A6A5A4A3A2A1。

本文设计的变幅杆为半波长变幅杆，变幅杆两端为自由状态，此时有边界条件F0=0和F11=0，代入式(4)，得

(5)

可推得

(6)

为避免变幅杆振动向主轴部件传递，现以拉爪和刀柄的结合面处作为半波长变幅杆的设计节点，见图3。此处理论振幅为0，应尽可能减小变幅杆对拉杆的影响。此时节面处的位移u5和力F5为

(7)

式中，Aβ=A5A4A3A2A1。

变幅杆大端为自由状态，F0=0，节面处位移u5=0，代入式(7)，得

(8)

可推得

(9)

式(6)和(9)是关于k,E,L,R,S的函数。E为弹性模量，由材料决定。由于超声波在不同阻抗的两种介质分界面处会发生反射造成能量损失[12]，因此变幅杆与刀柄选用相同材料，参数见表1。拉爪型号为精勤HSK-E32，刀柄型号为HSK32E-ER16M-60。变幅杆大端外圆半径R01=0.025 m，长度L1=0.01 m。将拉爪、刀柄及变幅杆大端各参数代入式(6)和(9)求解，得复合变幅杆圆锥段长度L=0.052 7 m，圆波数k=24.254 1，进而求得变幅杆工作频率f=kc/2π=19 886 Hz。根据工作频率设计相匹配的换能器，以便达到最好的振动效果。

表1 变幅杆材料参数Tab.1 Material parameters of the horn

2 仿真分析

2.1 主轴的临界转速

由于零件材料组织不均匀和加工误差等原因，轴类零件在回转时会因为离心力产生周期性干扰进而产生共振现象，降低机床寿命，甚至损坏主轴。因此，要使主轴的工作转速避开共振时的转速，即临界转速。通过分析主轴模态校核临界转速。本文设计的主轴为刚性轴，其转速低于一阶临界转速。根据功能需求和电机选型，额定转速为6 800 r/min，最大转速24 000 r/min。主轴的临界转速与频率存在以下关系[13]：

v=60f，

(10)

式中：v为主轴临界转速；f为主轴共振频率。将单个轴承简化为圆周方向均布的4个弹簧单元[14]，如图5所示。将弹簧与主轴连接处设置为轴向固定约束，从而限制主轴的轴向运动，弹簧另一端为完全固定约束。

图5 均布弹簧模型Fig.5 Uniform distribution of spring model

通过模态分析，得到主轴的前六阶模态，其频率和振型如图6所示。其一阶模态振型为转动，频率约等于0，不影响主轴的临界转速。表2为各模态振型及其固有频率对应的临界转速，由表2可以看出，其临界转速远远高于主轴的最大转速，符合设计要求。

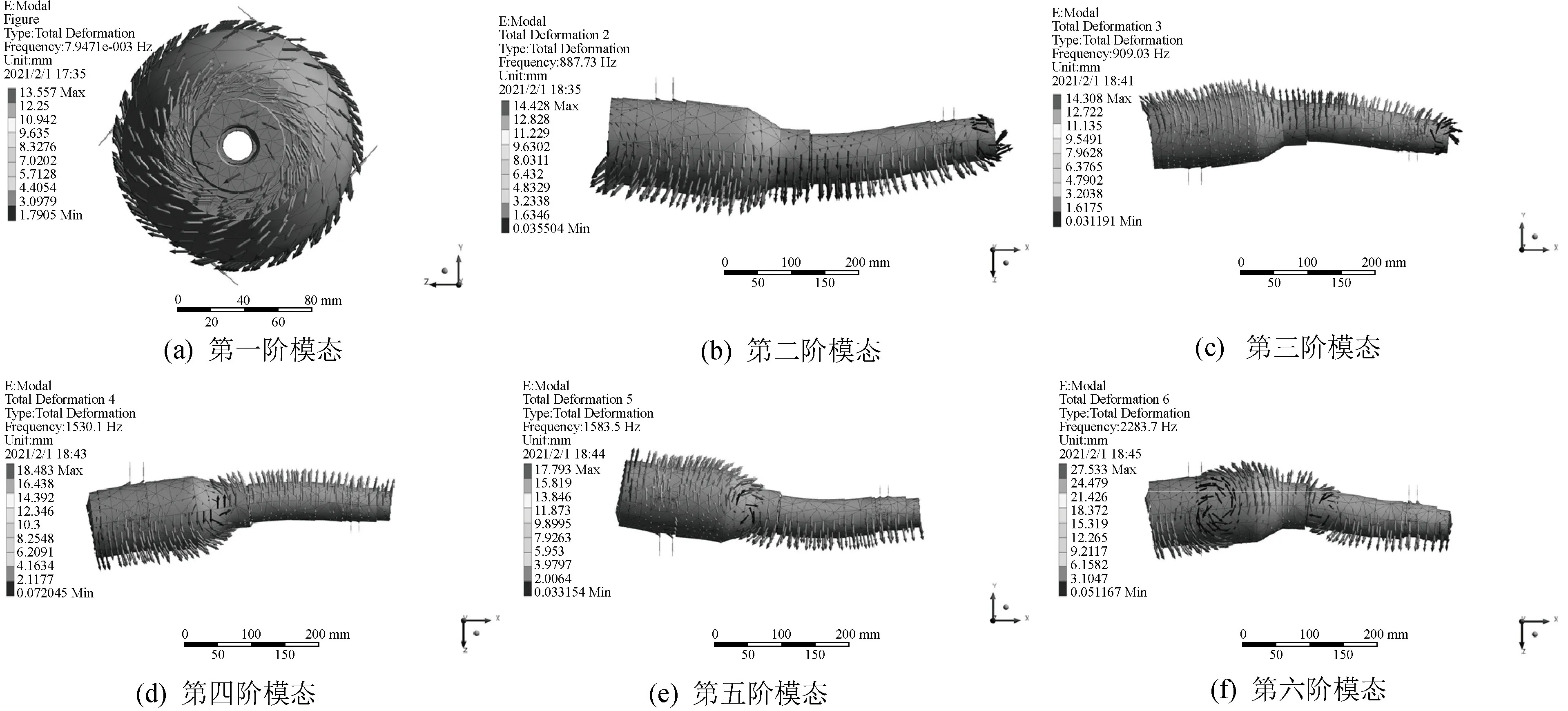
图6 主轴模态振型Fig.6 Modal shapes of spindle

表2 主轴临界转速Tab.2 Critical speed of the spindle

2.2 自由模态分析

通过变幅杆三维建模并定义材料参数后，采用软件默认方式进行网格划分，设定频率搜索为18 500～21 500 Hz，进行模态分析，得到一个模态振型，见图7。振幅最大值在刀具端部，并且刀柄与拉爪接触处振幅最小。仿真频率19 031 Hz，与计算结果误差为4.2%。考虑到计算过程中模型细节的简化，误差在合理范围内。图8为考虑法兰和拉爪的变幅杆自由模态，拉爪与变幅杆接触面设置为摩擦接触，摩擦系数0.1。图9为整个主轴的自由模态，可以看出，在变幅杆的共振频率内1主轴并没有发生共振，且两处轴承安装位置振幅约等于0。

图7 变幅杆自由模态Fig.7 Free mode of horn

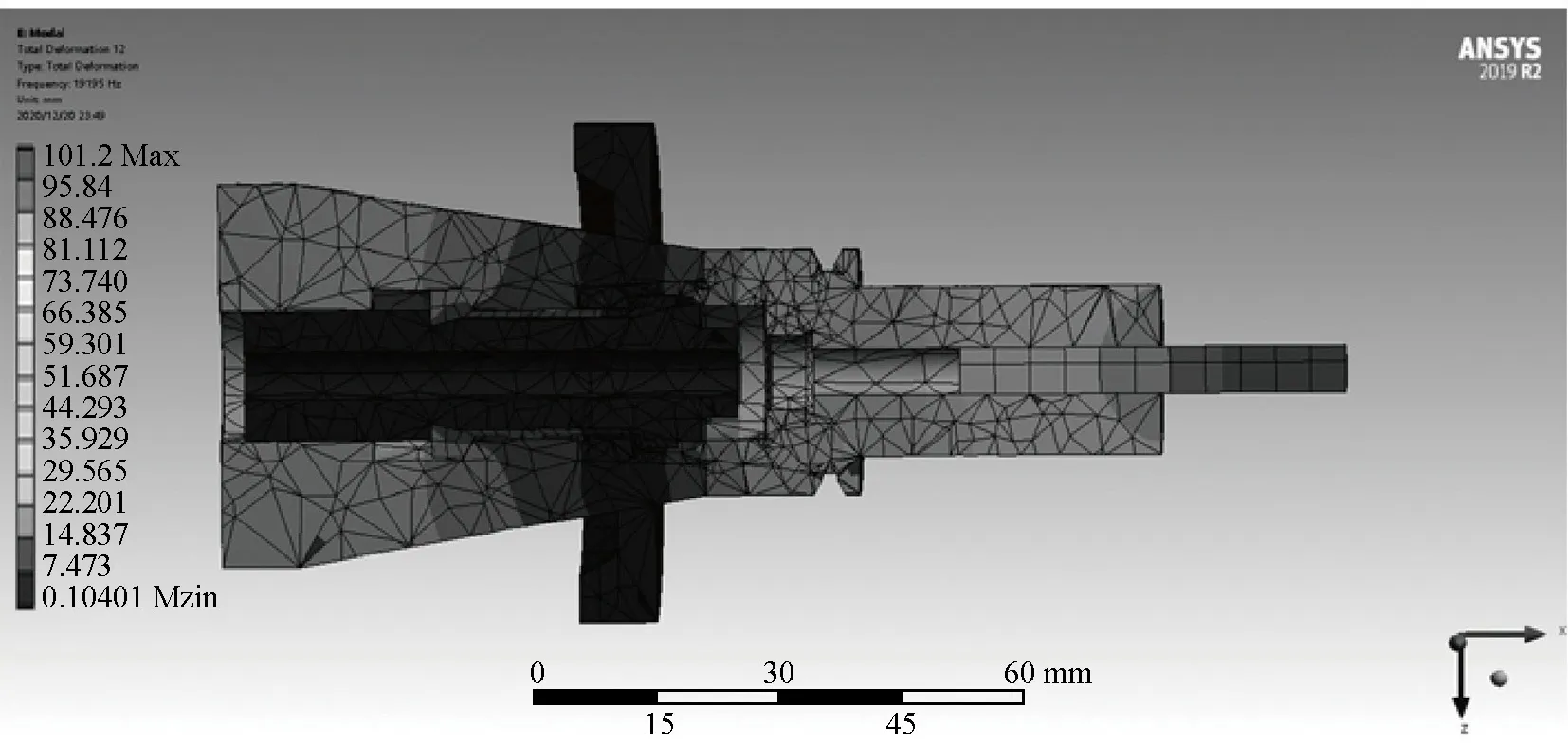
图8 考虑法兰和拉爪的度幅杆自由模态Fig.8 Free mode of horn withflange and clamping unit

图9 主轴自由模态Fig.9 Free mode of spindle

2.3 变幅杆的预应力模态分析

HSK刀柄的拉刀方式是通过拉杆后的弹簧提供拉力，经由拉爪内部结构将拉力放大，使刀柄与刀柄接口之间达到一定的过盈量。根据选用拉爪的型号，正常工作下拉杆提供的拉力为1 000 N，考虑拉爪结构较复杂，建模误差较大，因此直接对拉爪与刀柄接触面施加作用力。通过计算可知，该接触面上所受轴向力约为1 428 N，径向力约为2 474 N[15]。对变幅杆做预应力的模态分析，结果如图10所示。

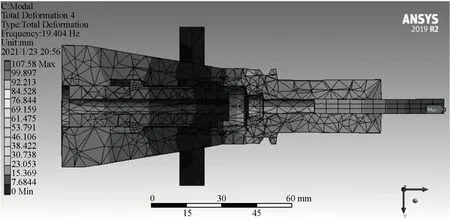
图10 变幅杆的预应力模态分析Fig.10 Pre-stress mode analysis of horn

预应力分析下的模态频率为19 404 Hz，相对于自由模态，其频率增加了1.9%。这是因为受拉力之后，拉爪与法兰之间的部分刚度增加，进而使固有频率增大。

3 变幅杆的振动测试

依据理论计算尺寸制作变幅杆及其他部件，搭建实验平台对理论计算和仿真结果进行验证。采用Impedance Analyzer PV70A型阻抗分析仪对制作的变幅杆进行阻抗分析，结果如图11所示。

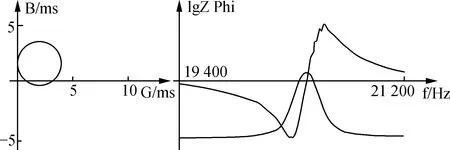
图11 阻抗分析结果Fig.11 Impedance analysis result

图11中的变幅杆谐振频率为20 552 Hz，实际测得频率与计算频率误差为3.3%，在合理范围内。结果显示导纳圆圆度较好，电导曲线正常，说明该变幅杆结构设计合理。

利用激光位移传感器对拉刀状态下的变幅杆刀具端部振幅进行测量，测量装置如图12所示。图13为振幅测量结果，该结果显示，刀具端部能产生稳定的周期性振动，振幅最大值5 μm，满足使用要求。

图12 振幅测量装置Fig.12 Amplitude measurement device

图13 刀具端部振幅Fig.13 Amplitude at the end of tool

4 结 论

(1)提出了一种适应加工中心自动换刀功能的超声加工电主轴，并对其主要结构进行了设计分析。该装置可以针对HSK32刀柄配合换刀机械手自动换刀，解决了传统超声加工中必须停机手动换刀的问题，可有效减少机床待机时间，提高机床利用率。

(2)分析了新型超声加工主轴的前六阶模态，得到了频率和振型。对主轴的临界转速进行了校核，证明该结构符合设计要求。

(3)设计了复合超声变幅杆，并通过有限元分析得出，在变幅杆节面处施加拉力后，频率有所上升，但振型没有发生变化，能达到理想的振动效果。变幅杆与主轴通过法兰连接，通过模态振型云图可以看出主轴轴承安装位置振幅约等于0，在装置达到理想振动效果的同时，可以有效避免变幅杆振动对主轴的负面影响。

(4)制作变幅杆，搭建实验台，通过试验测量变幅杆的阻抗和刀具端部振幅。刀具端部产生稳定的周期性振动，振幅最大值5 μm，实现了电主轴超声加工功能，并便于加工中心自动换刀。