不同因素对脉冲压力响应的影响规律研究
贾石川,胡立强,肖智勇,王刚,2,姜枫
(1.山东科技大学 山东省土木工程防灾减灾重点实验室,山东 青岛 266590;2.山东科技大学 矿山灾害预防控制省部共建国家重点实验室培育基地,山东 青岛 266590)
0 引 言
自从北美成功开发页岩气以来,页岩气等非常规能源受到了能源界的广泛关注[1]。中国页岩气可采资源量为1.5×1013~2.5×1013m3,与美国资源量相当,现采用大规模水力压裂和微地震监测技术进行开采[2]。中国在页岩气开发探索中形成了新的开采机制,提高了单井产能[3]。非常规能源包括煤层气、致密砂岩气和页岩气,为了减少对常规能源的依赖,非常规能源的商业化开发变得越来越迫切,渗透率通常被认为是开采的关键参数之一,是决定非常规能源商业开采可行性的重要因素[4]。实验室测量渗透率分为稳态法和非稳态法[5],渗流介质有煤油、水、气体等多种[6]。稳态法在不同驱替压力下监测流量,通过滑脱效应改进,得到绝对渗透率;非稳态法中的脉冲衰减法根据脉冲压力与时间的关系得到渗透率。在测量渗透率方法的发展过程中,由于脉冲法测量致密岩石渗透率(10-6~10 mD)[7]花费时间少,精度高,一直被广大学者采用和发展[8-13]。
脉冲法和稳态法的区别在于脉冲法不需要测量流速,只需要记录压力随时间的变化关系就可以测出渗透率[14],同时脉冲法在高围压条件下进行,更加符合现场情况。然而脉冲压力响应受到多种因素影响,包括岩样渗透率、孔隙度、横截面积、岩石体压缩性、基质压缩性以及测量所用的上下游储层体积等。页岩渗透率极低,即便采用脉冲法测量也需要很长的时间,且脉冲法对气密性要求很高。此外,孔隙度测量以及反映压力变化的压力传感器精度也会影响压力响应,实验装置的局限性也使得实验室研究各种因素对压力响应的影响变得困难。为了更好地分析压力响应,数值模拟方法更加实际可行。
LIN W[15]采用解析解和数值解求解了渗透率岩石的一维流体流动微分方程,然而在解析解中并未考虑下游储层的影响,其数值解直接采用TRUMP代码,未给出详细的推导;F.Civan[16]提出了用实用有限分析法求解微分方程的空间/时间解的数值方法,与基于分离变量和拉普拉斯变换的原始有限解析求解方法所产生的繁琐离散化格式相比,可以得到更加简便的离散化格式;王自明等[17]利用有限元与有限差分法求解流固耦合方程,交替迭代求解得到参数的解;刘文超等[18]通过有限差分法研究了不稳定渗流边界数值解,算法简单,但局限于低渗非达西流等。
综上所述,在多孔介质的渗流计算问题中,有限差分法求解偏微分方程研究较少。本文在F.Civan[16]提出的实用有限分析法求解微分方程的基础上,将其应用于多孔可压缩介质的一维瞬态流动的偏微分控制方程,提出用有限差分法求解非线性偏微分方程。此外,在MATLAB环境下编制计算程序代码,模拟求解脉冲压力随时间和空间的变化趋势。通过改变模型中的参数值,重点研究渗透率、孔隙度和上下游储层体积对脉冲压力响应的影响,以期为非常规储层能源商业化开采提供指导意见。
1 模型建立
在测量花岗岩渗透率时,W.F.Brace等[9]首先提出可压缩流体通过多孔可压缩介质的一维瞬态流动控制偏微分方程,将压力简化为距离x和时间t的函数,即
(1)
其中,L为试样长度,c与地质材料的储存性能有关,是一个与储层内部连接的孔隙度、基质和岩体压缩性、流体性能有关的函数[19]。
利用达西定律和质量守恒原理,试样在上下游储层的初始值可以简化为
p(x,0)=p0,0 (2) p(0,t)=pu(t),t≥0, (3) p(L,t)=pd(t),t≥0, (4) 式中,pu(t),pd(t)分别为t时刻上下游储层的压力。 式(2)表示t为0时岩心内部初始压力为p0,式(3)表示t时刻x=0处的压力为pu(t),式(4)表示t时刻x=L处的压力为pd(t),其中pd(0)=p0,pu(0)=p0+Δp。 老龄化为养老保障带来巨大压力。随着人口平均预期寿命的上升,越来越多的人开始享受养老保障的福利,但上交老年保险的比例不是很高,导致保险行业盈利受阻,甚至负盈利[5]。人口老龄化会对医疗保险和老年保险形成冲击,不能有效解决这个问题将给我国经济社会带来负面影响。 上下游储层的边界值可以简化为 (5) (6) (7) (8) (9) 式中:A,k,φ分别为横截面面积,渗透率和孔隙度;Vu,Vd分别为上下游储层体积;μ和β分别为测试流体的黏度和压缩系数;βb为试样体压缩系数;βs为固体基质的压缩系数。 由于式(1)无法直接求解,且给出的解析解形式复杂,所以人们很难正确理解流体随时间和空间变化的流动行为。此外,边界条件的复杂性也增加了解析解的难度。为了正确理解可压缩流体通过多孔可压缩介质的一维瞬态流动时空特性,采用有限差分法分析偏微分控制方程,并通过编制MATLAB程序将非线性偏微分方程代码化,加入边界条件和初始条件进行数值计算。 压力p(x,t)对x进行泰勒多项式展开, (11) (12) 其中o(Δx3)为x的三阶等价无穷小。将式(11)与(12)相加, (13) 忽略x的高阶等价无穷小,式(13)可改写为 (14) 压力p(x,t)对t进行泰勒多项式展开, (15) 忽略t的二阶等价无穷小,将式(14)和(15)代入式(10),则得到有限差分形式为 (16) 利用有限差分法计算岩心上下游边界条件的压力梯度[20], (17) (18) 故上游边界条件式(5)有限差分形式为 (19) 下游边界条件式(6)有限差分形式为 (20) 对式(16)、式(19)~(20)通过MATLAB编程进行时间步求解,可得到压力随时间和空间的变化曲线。 非常规储层中的一些参数如渗透率、孔隙度等,对于不同岩石其数量级相差很大,此外在实验室测量过程中,试样尺寸、固体压缩性、基质压缩性和上下游储层体积大小均对压力响应具有一定影响。本文研究对象主要为煤岩,采用氦气作为渗流介质,数值模拟基本参数如表1所示。为了研究这些参数对压力响应的影响,基于建立的数值模型,在MATLAB环境下编程进行计算,计算过程如图1所示:首先根据表1输入初始计算参数,选择合适的时间步长dt与距离步长dx,计算中选取的最大时长为10 000 s,时间步长为1 s,L=10 cm,距离步长为0.05 cm;其次输入上下游的边界条件差分形式,即式(19)~(20),最后输入式(16),得到时间域1:t_len-1与空间域1:x_len-1上的压力值。 图1 模型计算流程图Fig.1 Flow chart of model calculation 表1 数值模拟基本参数Tab.1 Basic parameters used in numerical simulation 试样βb、βs数值很小,计算过程中对c的影响可以忽略不计。假设氦气压缩系数和黏度系数保持不变,本部分仅研究渗透率、孔隙度和储层体积3个因素对压力响应的影响。 数值模拟的介质为煤岩,渗透率为0.000 1~100 mD[22],分别选0.1,0.5,1,2 mD进行计算,结果如图2所示。由图2(a)可知,随着渗透率降低,压力减小的速度变缓,表明到达最终平衡的时间增长。由图2(b)可以看出,不同渗透率下的压力响应均包含线性区域和非线性区域,且非线性区域出现的时间较短。非线性区域代表初始脉冲时,试样中的气流处于非稳流状态,随着脉冲进行,试样内的气流逐渐变成稳流状态,即图2(b)中的线性区域。随着渗透率增大,线性拟合曲线的斜率绝对值变大,表明所需平衡时间减小。此外,线性区域出现的时间随着渗透率降低而滞后,表明在其他因素相同的情况下,平衡压力在低渗透率的岩石中达到稳定梯度下降所需时间较长。不同渗透率下模拟所用各参数的值见表2,可以看出渗透率同时影响c与λu,λd,并与这3个数值呈负相关关系。 图2 渗透率对脉冲压力响应的影响曲线Fig.2 Effect curves of permeability on pulse pressure response 表2 不同渗透率下模型中各参数的值Tab.2 Values of various parameters of the model under different permeability 由式(7)可知,当渗透率保持不变时,随着孔隙度增大,c也逐渐增大,数值模拟中选择0.5%,2%,5% 3组孔隙度进行计算,模拟所用参数如表3所示。图3(a)显示了不同孔隙度下的脉冲压力响应,φ=0.5%时,脉冲压力下降速度最慢,但其平衡时间明显小于其他两组数据。随着孔隙度增大,脉冲压力在前期下降速度逐渐增大,当上下游储层脉冲压力接近时,孔隙度较大的岩样脉冲压力平衡所需时间明显变长。 表3 不同孔隙度下模型中各参数的值Tab.3 Values of various parameters in the model under different porosity 一般认为孔隙度对渗透率有一定影响,为了简化分析,本文仅考虑单变量造成的影响,即不考虑各因素间的相互影响。当渗透率保持不变时,孔隙度增加势必会引起其他改变。分析认为,岩样内的孔隙主要分为贯通的孔隙和封闭的孔隙。结合图3(b)可知,孔隙度较大时,气体渗透岩心过程达到稳流状态所需的时间更长,表明相同渗透率下,孔隙度大的岩心其内部孔隙构造更复杂,上下游压差较小时,平衡所需时间更长。孔隙度较大使得气体在最初渗透过程中脉冲压力变化更为明显。 图3 孔隙度对脉冲压力响应的影响曲线Fig.3 Effect of porosity on pulse pressure response 相对于不同的上下游储层体积,相同的储层体积不仅可以简化计算方法,还能够减少实验时间[23]。常规的压力脉冲装置上下游储层体积相同,因此,本部分主要研究上下游储层体积相同时,不同的储层体积对脉冲压力响应的影响。模拟选用实验室常用储层体积5,50,200 cm3进行计算,其他参数如表4所示。图4(a)为储层体积对脉冲压力响应的影响,当上下游储层体积为5 cm3时,脉冲压力下降速度最快,且平衡所需时间最短,随着储层体积增大,压力变化幅度逐渐减少,最终平衡时间也随着储层体积增加而增加,表明较小的储层体积可以缩短平衡时间。储层体积过小也会存在一些弊端,如图4(b)所示,储层体积越小,达到稳流状态所需时间越长,并且较小的储层体积对于试样的非均质性更加敏感,当采用小的储层体积时,脉冲压力变化引起的温度变化以及外界扰动等因素对测量结果造成的影响将更加显著。此外,当孔隙体积保持不变时,储层体积较小时相同的孔隙体积误差引起的渗透率计算误差更大[24],因此,在实验室进行致密岩石渗透率实验时应选择合适的储层体积进行测量。 表4 不同储层体积下模型中各参数的值Tab.4 Values of parameters in the model under different reservoir volumes 图4 储层体积对脉冲压力响应的影响曲线Fig.4 Effect curves of reservoir volume on pulse pressure response (1)提出了采用有限差分法计算可压缩流体通过多孔可压缩介质的一维瞬态流动非线性偏微分方程,并在MATLAB环境下研究了渗透率、孔隙度、储层体积对脉冲压力响应的影响。 (2)随着渗透率增加,压力减小速度变快,所需平衡时间变短。在脉冲过程中,气体达到稳流状态的时间随着渗透率增加而减少。 (3)脉冲压力在孔隙度较大的试样中前期变化更大,上下游储层压力差较小时,平衡时间与孔隙度成正比,表明渗透率、横截面面积、上下游储层体积保持不变时,孔隙度越大,其内部孔隙越复杂,脉冲压力主要经历快速减少阶段和缓慢减少阶段。 (4)上下游储层体积相同时,随着储层体积增加,平衡所需时间变长,最终平衡压力增大,气流达到稳定状态时间变短。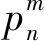

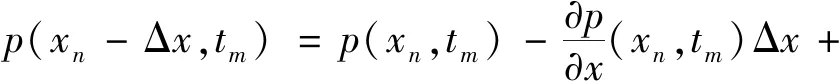


2 模型参数分析


2.1 渗透率对脉冲压力响应的影响


2.2 孔隙度对脉冲压力响应影响
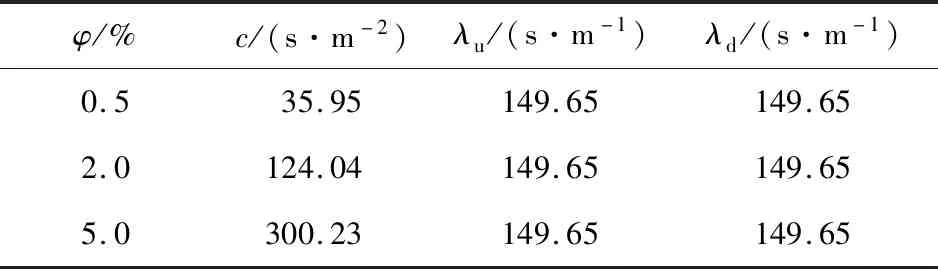

2.3 储层体积对脉冲压力响应影响


3 结 论

