弹性支承上弹性转动约束矩形薄板线性荷载压屈分析

吴韬，莫时旭，郑艳

(桂林理工大学 土木与建筑工程学院，广西 桂林 541004)

0 引 言

随着钢材强度提高，钢结构在工程中应用越来越广泛，同时由于其加工性能的改善，钢结构设计逐渐趋于轻型化、薄壁化，薄板钢结构的稳定性问题也越来越受到重视。在工程中，如方钢管混凝土柱的侧板、部分充填混凝土-钢箱组合梁的腹板和顶板等钢板都易“鼓包”，从而发生局部屈曲，因此建立相关局部屈曲强度计算公式，研究合理的截面尺寸具有重要的意义。

近年来，国内外学者从不同角度出发，提出多种矩形薄板屈曲问题研究方法。XIANG Y[1]和詹豪等[2]分别利用状态-空间向量法研究了刚性和弹性支承上连续矩形板的屈曲问题；黄小林等[3]基于Galerkin法(伽辽金法)计算了不同组合边界条件下复合材料板动力稳定问题的临界屈曲荷载；谈梅兰等[4]利用Galerkin法求解了抛物线和余弦曲线分布压力下四边简支矩形板的屈曲问题；史旭东等[5]、甘立飞等[6]运用有限元法研究了矩形薄板在面内非均匀压力下的屈曲问题。

薄板屈曲的另一大主流研究方法是能量法，主要是Rayleigh-Ritz法(瑞利-里兹能量法)。根据屈曲模态不同，矩形薄板的屈曲理论可分为两类。一类是双向屈曲问题：Timoshenko等[7]利用能量法研究了周边不同边界条件下，受面内不同作用力的矩形薄板弹性屈曲理论模型；QIAO P Z等[8-9]根据屈曲模态提出多种挠曲面函数，研究了四边受均布压力四边弹性转动约束矩形板的屈曲和受剪切荷载两对边简支两对边弹性转动约束矩形板的临界屈曲荷载；刘沐宇[10]采用里兹法推导了弹性转动约束的钢混组合梁腹板在弯曲、剪切荷载单独作用下的临界屈曲应力。另一类是单向屈曲问题：H.D.Wright[11]研究了钢管约束混凝土的局部屈曲问题；毛佳等[12]运用里兹能量法获得了弹性支承上非加载边弹性转动约束均匀受压矩形板的临界荷载计算公式；郑艳等[13]研究了刚性支承上非加载边弹性转动约束受面内线性压力作用下的矩形板局部屈曲问题。

国内外学者对弹性支承上弹性转动约束边界受面内线性压力作用矩形薄板的屈曲问题研究尚少，对于复杂边界条件下的压屈问题多依赖试验和有限元数值分析[14-15]，这使得参数分析有较大局限性。获得具有弹性支承和弹性转动约束边界薄板受线性压力下的屈曲系数解析解，研究满足该边界条件的理论公式极具意义，因此，本文运用Rayleigh-Ritz法探究弹性支承上边界弹性转动约束薄板的屈曲模式，获得临界屈曲系数的理论计算公式，并采用壳单元和弹簧单元建立相关有限元模型，验证本文理论计算的适用性和正确性，还对不同支承刚度、不同转动约束刚度下的临界屈曲系数进行了参数分析。

1 弹性支承上弹性转动约束线性受压矩形薄板屈曲分析

1.1 计算模型以及挠曲面函数的选取

使用静力法求解板的屈曲问题，对相应荷载和边界条件下的薄板弯曲平衡微分方程(1)求积分，可得到薄板的挠曲面函数，

(1)

作为高阶偏微分方程，求解比较困难。瑞利-里兹法(Rayleigh-Ritz Method)作为应用势能驻值原理求解稳定问题的一种近似方法，采用具有广义坐标的位移函数近似代替真实的位移曲面方程，也即将泛函变分问题转化为求解函数极值问题，将求解偏微分方程变为求解代数方程来处理。

为了满足弹性转动约束的边界条件，选取挠曲面函数必须满足一定条件。如图1所示，通过选取带参数的多项式函数模拟y方向上的弹性转动边界[9]，选取一般三角级数模拟x方向上的简支边界和双向屈曲模态，则弹性支承上弹性转动约束矩形薄板压屈时面外位移函数为

(2)

其中，

(3)

(4)

式(3)中，为了构造弹性边界的特征函数，考虑幂级数[12]

(5)

将式(5)代入式(3)，再将式(3)与式(4)代入式(2)，可得弹性转动约束受压矩形薄板的挠曲面函数

(6)

式中：w为挠曲面函数；m，n分别为x，y方向的屈曲半波数；am为广义坐标；a为板长；b为板宽；N为薄板非加载边的边界条件方程个数。

如图1所示，矩形薄板厚度为t；弹性支承刚度为k0；非加载边y=0，y=b的弹性转动约束刚度为ky。为方便分析，假设薄板底面和上下边界均布两种刚度的弹簧，则底面和上下边单个弹簧刚度的量纲为[力]/[长度]。

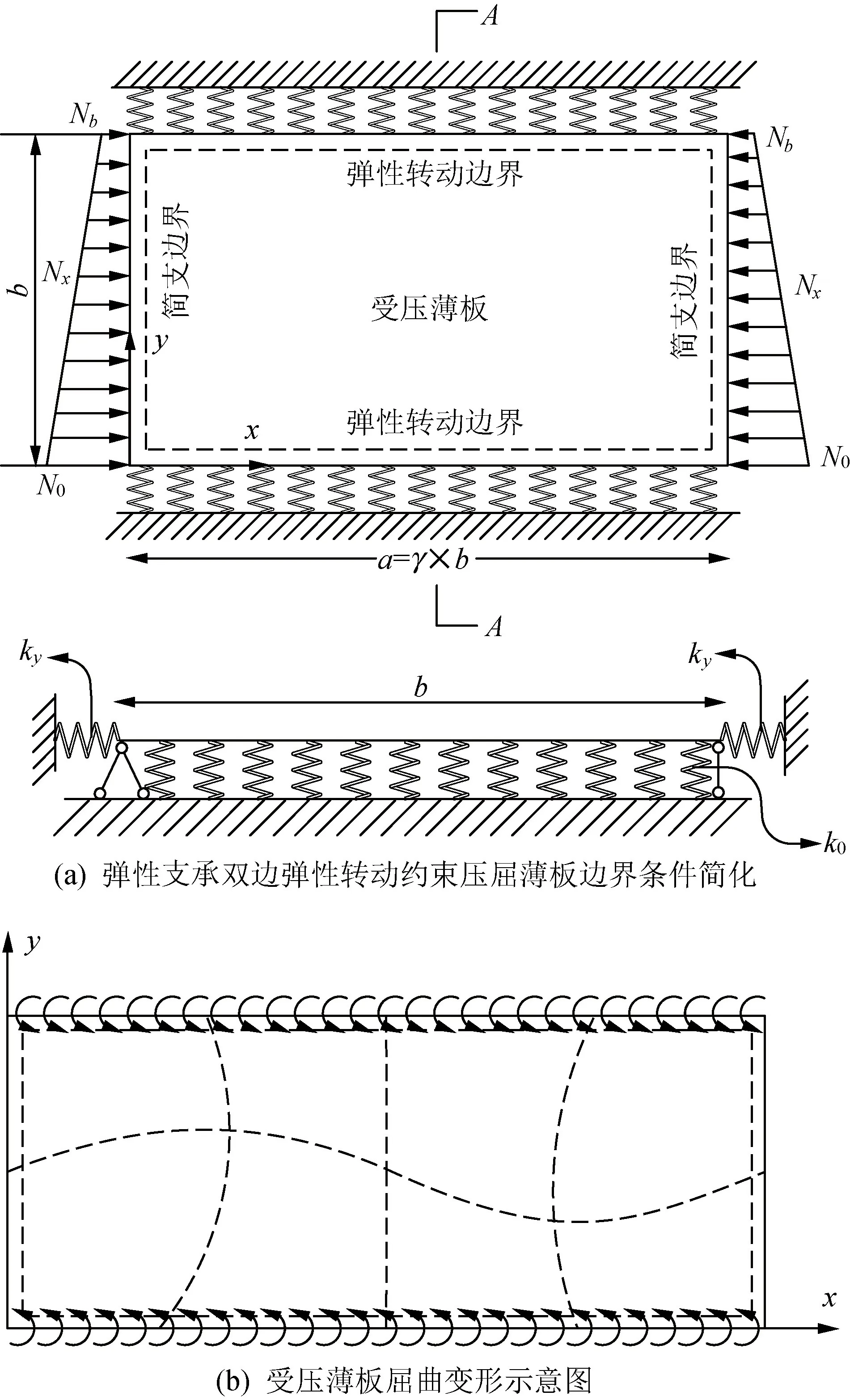
图1 弹性支承上双边弹性转动约束矩形薄板受压屈曲模型Fig.1 Local compressive buckling mode of rectangular plate with rotationally restrained sides on elastic base

加载边x=0，x=a受面内荷载Nx作用，沿作用边线性分布，单位板宽的荷载表达式为

(7)

(8)

其中，λ=(σ0-σb)/σ0为荷载梯度。

显然该位移函数满足加载边面外位移为0的边界条件。根据非加载边受弹性转动约束的边界条件，面外位移为0且板边弯矩与约束力矩相等，即满足

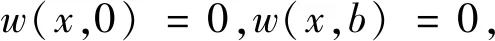
(9)

(10)

(11)

根据非加载边的边界条件方程个数，式(6)中N=4，可改写为

(12)

式中：m为x方向的屈曲半波数；a0～a4由式(9)确定。

将式(12)代入式(9)～(11)，求出待定系数a0～a4，则挠曲面函数可表示为

(13)

式中：bm=a1am；χ2为无量纲弹性支承刚度系数，

(14)

1.2 压屈薄板各部分能量及其变分

弹性支承的支承势能为

(15)

对式(5)求一阶变分为

(16)

薄板产生弹性屈曲变形的弯曲应变能为

(17)

对式(17)求一阶变分为

(18)

上下边界受弹性转动约束的势能为

式(19)的一阶变分为

(20)

面内线性压力荷载所做的功为

(21)

对式(21)求一阶变分，即

(22)

根据最小势能原理有

(23)

其中，Π=Uk+Ue+UΓ-WN，为薄板产生屈曲变形时的总势能。于是

(24)

将求解泛函变分问题转化为求解关于bm的特征值问题，由式(24)得关于bm的一个线性方程组。为使线性方程组存在非0解，其系数矩阵的行列式必须为0，由此可求得矩形薄板在线性压力作用下发生屈曲的临界荷载Nx，

(25)

单位厚度的线性荷载

(26)

其中，κ为屈曲系数。

2 弹性支承上弹性转动约束矩形薄板线性受压屈曲参数分析

2.1 矩形薄板线性受压临界屈曲系数解析解

为了方便描述薄板单元的屈曲行为，利于后续参数化研究，根据文献[13]，引入以下无量纲弹性支承刚度系数

(27)

将式(13)代入式(15)～(24)，获得弹性支承上弹性转动边界线性受压矩形薄板的屈曲系数解析解

(28)

由此可见，κ是关于半波数m、刚度系数(χ1，χ2)、长宽比γ和荷载梯度λ的函数。

取λ=1，当χ1，χ2为各种情况时，根据式(28)对每一半波m=1,2,3，…绘制出κ与γ的关系曲线，如图2所示。χ1=χ2=0时，板的临界屈曲系数约为8.003。

各屈曲半波数m和纵横比γ相关，若m=p-1与m=p两支曲线相交，则令

(29)

其中，p-1为前一半波数。曲线交点(γp-1,p,κp-1,p)应满足式(27)。代入式(26)，可得

(30)

(31)

(32)

其中，式(32)为对p(γ)取整。

当给定屈曲半波数p-1，p时，式(30)给出矩形薄板κ-γ曲线交点纵横比γ；同样，不论纵横比γ如何取值，矩形薄板在x方向的屈曲半波数始终等于整数m。以图2(a)为例，p=4时，由式(30)计算可得γ(4)=(31/21)1/4π≈3.463，即半波数m=3，4图像分支交点横坐标为3.463；γ=4.8时，由式(29)计算可得p(4.8)=5.328，取整得m=5，显然薄板的屈曲半波数为5。

图2 κ与γ关系曲线Fig.2 Relation curves between κ and γ

2.2 矩形薄板线性受压屈曲强度参数分析

当Nx取得最小值(Nx)cr时，纵横比为γcr。令∂κ/∂γ=0，代入式(28)得

(33)

将式(33)代入式(28)，得到临界屈曲系数

(34)

根据式(28)，利用基本不等式求解κ对γ的极小值，

(35)

2.2.1γcr与χ1,χ2的关系

由式(33)可得m=1时临界长宽比γcr与刚度系数χ1,χ2的关系曲线，如图3所示。χ2=0,χ1=0,10,100时，γcr分别为1.000，0.549，0.315。由此可见，相同屈曲半波数时，γcr随着χ1,χ2的增大而减小。χ1一定时，γcr随着χ2的增大而减小；χ1增大时，γcr-lgχ2曲线整体下降，且γcr的变化幅度减缓；当χ1增大到100时，γcr几乎不随χ2变化成为定值0.31，可见刚度系数χ1比χ2对γcr的影响很大。

图3 γcr与χ1,χ2的关系曲线Fig.3 Relation curves betweenγcrandχ1、χ2

2.2.2κcr与χ1,χ2的关系

由式(34)得到λ=1时临界屈曲系数κcr与刚度系数χ1,χ2的关系曲线，如图6所示。对χ2采用对数坐标，可以看出每一条κcr-lgχ2曲线都存在上、下两条渐近线，分别代表矩形薄板边界固支和简支时的临界屈曲系数κcr。

以χ1=0为例，χ2<0.8时，κcr趋近于下界渐近线，由表1可知，此时κcr取简支边界(χ2=0)的κcr值，误差为6.56%；χ2>100时，κcr趋近于上界渐近线，由表2可知，此时κcr取固支边界(χ2=∞)的κcr值，误差为3.75%。由此可见，χ2<0.8的板可视作简直边界板；χ2>100的板可视作固支边界板。

表1 简支边界κcr的取值误差Tab.1 Simply-supported boundary value errors of κcr

表2 固支边界κcr的取值误差Tab.2 Clamped-supported boundary value errors of κcr

χ2取0.8～100时，κcr随χ2的增大而显著提高，且κcr与lgχ2呈近似线性关系，如图6(a)，利用线性回归得到简化回归公式

图6 κcr与χ1，χ2的关系曲线Fig.6 Relation curves between κcr and χ1 、χ2

(36)

将式(36)代入式(26)，得到矩形薄板的受压屈曲强度

不同弹性支承刚度系数χ1、不同荷载梯度λ下，板的屈曲强度系数与弹性边界转动刚度系数χ2存在明显差异，χ1和λ取值为各种情况时，板的临界屈曲系数计算公式如表3所示。

表3 特定支承刚度系数下薄板屈曲强度系数κcrTab.3 Buckling coefficient κcr of plates under specific support stiffness coefficient

2.2.3κcr与λ的关系

由式(34)可得刚度系数χ1,χ2各种情况时临界屈曲系数κcr与λ的定量关系，如图4所示。λ=0，即矩形薄板均匀受压情况下，χ1=0,χ2=0,10,100时，κcr分别为4.002,5.600,6.728，κcr随χ2增大而递增；当χ2=0、χ1=0,10,100时，κcr分别为4.002,8.634,22.100，κcr随χ1增大而递增，且增长幅度远大于χ2对κcr的影响。对于图中的每一支曲线，λ=0时，临界屈曲系数κcr最小，且随着λ增大κcr逐渐提高；对于χ1=χ2=0，当λ=100.2≈1.58时，κcr迅速提高，取对数后变化趋势更加明显，这是因为矩形薄板受拉区显著增大，从而抑制了薄板的受压屈曲。

图4 κcr与λ的关系曲线Fig.4 Relation curves betweenκcr and λ

荷载梯度λ不同，矩形薄板受载边面内受压形式存在差异。以λ=0,2/3,1,4/3为例，受载边压力形式如图5所示。λ>1时，受载边同时受压力和拉力作用。

图5 几种不同面内受压薄板Fig.5 Several plates under in-plane compression

3 有限元分析

3.1 有限元模型的建立

采用有限元软件ANSYS，分析在弹性支承上弹性转动约束受压矩形薄板的屈曲问题，并与本文理论解比较分析其适用性。薄板模型采用Shell63四节点弹性壳单元；对于弹性转动边界和弹性支承基底约束，采用两种Combin14弹簧-阻尼器单元，单元属性分别定义沿板边的转动自由度(Rotx)和垂直于板面方向的自由度(Uz)，使弹簧单元只有绕坐标轴的转动刚度或沿坐标轴的轴向拉压刚度。Combin14单元为二节点单元，在构造弹簧时，应完全约束其中一个节点的自由度。

为满足多参数重复分析的需要，利用ANSYS参数化设计语言APDL编写建立模型和特征值屈曲分析的命令流程序。首先生成全部节点，然后建立相关单元，集成相关参数的控制面板，能方便快捷地建立有限元模型。设定主要参数为χ1，χ2和γ，通过变换不同参数，计算不同约束条件下的受压屈曲荷载。薄板的弹性模量E=2.1×1011Pa，泊松比μ=0.3，板厚t=0.003 m。为方便起见，板宽b取定值1 m，根据薄板的长宽比γ确定板长a。在模型中，沿x轴方向的板边为弹性转动约束边界，同时板四边简支，对于不与薄板相连的弹簧单元节点，约束其全部自由度。

图7为λ=0，χ1=10时κcr-lgχ2的理论解和有限元数值模拟结果对比，可以看出理论解和有限元结果趋势一致，χ2<10时，误差很小；χ2较大时，理论解和有限元解的误差偏大，但整体误差不超过1.43%，两者吻合良好，本文理论计算公式可以满足工程精度要求。

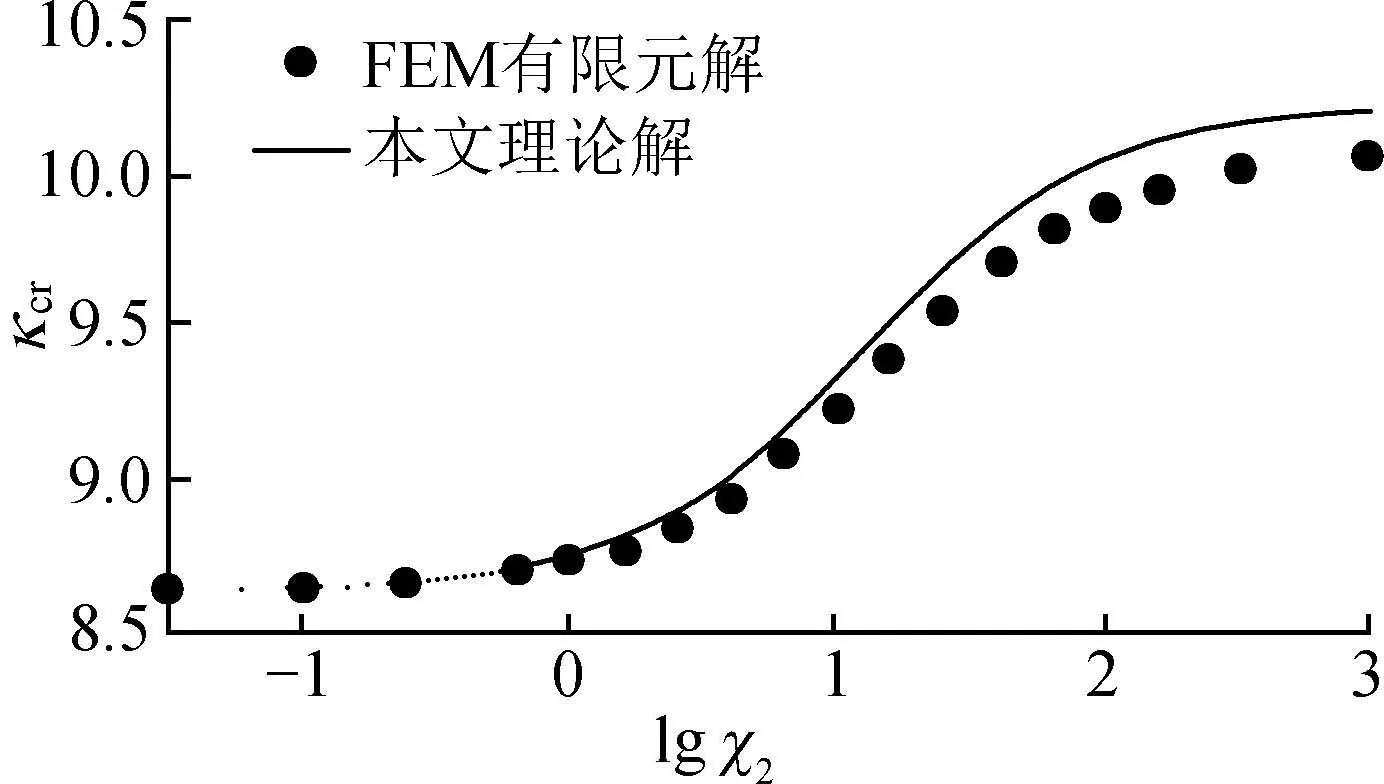
图7 κcr-lgχ2计算结果对比(λ=0,χ1=10)Fig.7 Comparison of κcr-lgχ2 calculation results

图8给出了弹性支承、弹性转动约束薄板线性受压屈曲的典型模态，λ=0，γ=3，χ1=χ2=10时发生6个屈曲半波。根据式(31)，令γ=3，p(3)=6.227，取整得m=6，与有限元模拟结果一致。此时板的临界屈曲特征值为47 197.4 N/m，相应临界屈曲系数为9.21。

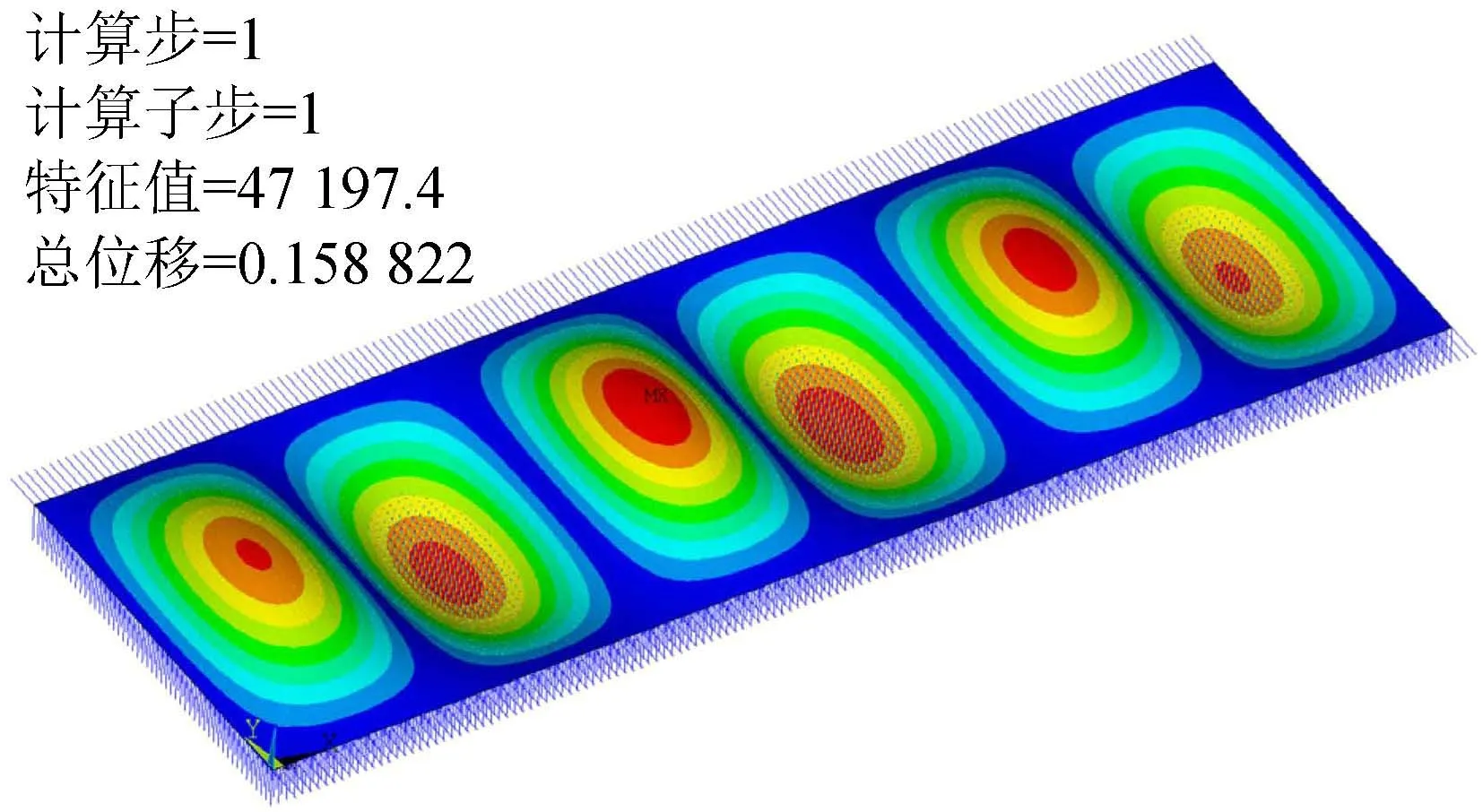
图8 矩形薄板受压屈曲模态Fig.8 Pressure bulking modes of rectangular plate

3.2 理论解的优化

表4为修正前理论解和有限元数值解的结果比较。由表4可知，当λ在较小范围内时，理论界与有限元解的误差较小，λ>1时，两者误差明显增大，并且随着χ1增大会产生更大误差。这是因为，λ=0时，薄板受均匀压力作用，屈曲发生面外的位移区域在整个薄板平面内，这与假定的薄板挠曲面函数式(11)吻合一致；随着λ增大，薄板不再受均匀压力作用，当0<λ<1，λ=1，λ>1时分别受如图9所示的梯形荷载作用、三角荷载作用和拉压同时作用，此时薄板屈曲发生面外位移的区域不在整个板平面内，而是在局部压力较大的区域，如图9(d)所示，发生屈曲区域集中在受压较大的y=0侧，这与构造的挠曲面形函数不完全吻合，从而导致理论解的临界屈曲系数偏大。

图9 荷载梯度各情况下有限元模拟(χ1=100,χ2=10)Fig.9 FEM simulations of several load gradients

表4 修正前理论解与有限元数值结果对比Tab.4 Comparisons between theoretical solution and finite element numerical results before revise

通过对比研究理论解和有限元解，修正后的临界屈曲系数公式为

(38)

(39)

aa 中：err为λ和χ1的函数；a为χ1的函数，

(40)

(41)

λ=1,4/3时，修正后的理论解与有限元结果对比见表5，误差在4.7%内，可满足工程精度要求。

表5 修正后理论解与有限元数值结果对比Tab.5 Comparisons between the modified theoretical solution and the finite element numerical results after revise

4 结 论

(1)提出满足矩形薄板受面内线性压力屈曲变形特点的挠曲面函数，通过利用瑞利-里兹能量变分法导出了弹性支承上弹性转动约束矩形薄板在线性压力荷载作用下的临界屈曲系数理论计算公式，形式简洁，便于应用，为进一步分析匀质矩形薄板在复杂边界条件下的压屈问题提供了理论依据。

(2)通过对屈曲理论解求极值，分析了临界屈曲系数随χ1，χ2的变化规律，并建立相应有限元分析模型，结果显示，λ<2/3时，误差不超过2%；荷载梯度较大时，采用带有修正项的临界屈曲系数，此时与有限元解的误差小于4.7%，证实了本文理论计算的可行性。

(3)在双刚度系数的参数分析中，基底支承刚度χ1比双边弹性转动约束刚度χ2对临界屈曲荷载的影响大，板件宽厚比一定时，提高弹性支承刚度可大大提高矩形薄板的抗屈能力。弹性转动约束刚度系数χ2在0.8～100内对矩形薄板受压稳定性能影响显著，χ2<0.8时，可视为简支边界，χ2>100时，可视为固支边界，实际工程结构中薄板屈曲的边界条件应按弹性转动约束考虑。