基于骨架关键点重规划的Voronoi图法路径规划

朱建阳 张旭阳 蒋 林 李 峻 雷 斌

(1.武汉科技大学冶金装备及其控制教育部重点实验室, 武汉 430081；2.武汉科技大学机器人与智能系统研究院, 武汉 430081；3.武汉科技大学机械传动与制造工程湖北省重点实验室, 武汉 430081)

0 引言

根据对环境信息掌握的程度，机器人路径规划可分为基于环境先验信息完全已知的全局路径规划和基于传感器信息的局部路径规划[1]。全局路径规划大多都是基于栅格法实现的，例如主流算法中的A*算法和Dijkstra算法，但是在栅格法中，栅格粒度越小，栅格图中障碍物位置会越精确，但需要的存储空间会越大，算法的搜索范围将会指数级扩大；栅格粒度越大，最终搜索出的路径就越不精确。确定栅格尺寸是栅格法的重要问题[2]。

在LOZANO-PEREZ[3]提出了路径规划中构型空间的概念后，构型空间法逐渐成为了路径规划的一种重要方案，构型空间法的出现，使路径规划方案有了新的选择，不再完全依赖受限于栅格尺寸的栅格法方案。Voronoi图法就是一种典型的构型空间法，Voronoi图法就是连接机器人的起始点和终点到已经生成的Voronoi图上，由此生成整体路径[4]。每次规划时只需要通过图搜索法找到起点和终点到Voronoi图的最短路径，中间部分路径依据Voronoi图生成。这种路径生成方式与栅格法中对整个栅格图进行搜索计算量减小了很多，实时性较好，生成的路径比较安全，远离障碍物。近年来一些学者针对Voronoi图法进行了改进，MAGID等[5]提出了一种利用全局信息构建Voronoi图，然后通过局部地区的参数调整进行优化的一种移动机器人路径规划算法，虽然生成的路径较为简洁，但是路径弯曲，存在较大转角，对机器人导航效率有较大的影响。蒋林等[6]提出一种改进骨架提取的Voronoi路径规划算法，该算法首先对地图进行处理，去除地图中的的噪点，解决了Voronoi地图臃肿的问题，但该算法同样存在生成路径曲折，路径长度冗余，机器人导航过程中实时性差、转折较多、耗时较长等问题。

以上研究都针对Voronoi的缺点进行了优化，但是优化后的结果都存在相同的问题，即Voronoi地图路径弯曲冗余，依据Voronoi地图进行规划时实时性差，规划出的路径较长，导致机器人导航过程中的时间成本较高。本文针对该问题，在当前研究基础上提出在生成的弯曲的Voronoi图中寻找出关键点，确定关键点之间的连接关系，然后进行重规划，精简全局Voronoi地图，并对依据重规划的Voronoi地图生成的路径进行降梯度采样，平滑路径，以实现在路径规划过程中快速搜索出优质路径。

1 栅格地图预处理

机器人通过建图算法构建环境栅格地图，地图以3色灰度图的形式呈现出室内环境轮廓。如图1a所示，地图上共有黑色、白色、灰色3种颜色，其中黑色为不可行区域，白色为可行区域，灰色为未知区域[7]。由于构建的栅格地图存在毛边，并且边界可能出现未完全封闭的情况，所以需要对地图进行预处理。

1.1 地图二值化

栅格地图为包含黑、白、灰3种颜色的灰度图，如图1a所示，其中黑色像素值为0，白色像素值为255，灰色像素值为205，首先设置阈值为200，依次对地图中的每个像素值进行二值化处理。二值化处理后的图像中数据量大为减少，并且能够更加清晰地凸显出地图中环境边界的轮廓[8]，如图1b所示。

1.2 地图的膨胀腐蚀

在得到二值图后需要对图像进行腐蚀和膨胀[9]，所谓腐蚀和膨胀就是对像素值都为255的白色区域进行处理。如图2a所示，假设白色区域为A，定义一个结构元素B，依次遍历A中的像素，在遍历时将B的中心与A的像素点重合[10]，求出此时结构元素B覆盖区域最小的像素值，并将该值赋予此刻结构元素B所覆盖的所有像素，如果结构元素B覆盖区域中有黑色像素值0，则此刻结构元素B覆盖区域的像素值将都变为0，即该覆盖区域中的白色会变为黑色，当遍历完成后，白色区域会缩小一圈，因此该过程被称为腐蚀，整个计算过程中不会改变原始数据，输出的新图像矩阵为新生成的单独矩阵[11]。如图2b所示，若在遍历时求出此时结构元素B覆盖区域最大的像素值，并将该值赋予结构元素B覆盖的所有像素，如果结构元素B覆盖区域中有黑色像素值0，则此刻结构元素B覆盖区域的像素值将变为255，则该覆盖区域中的黑色会变为白色，当遍历完成后，白色区域会扩大一圈，因此该过程被称为膨胀。

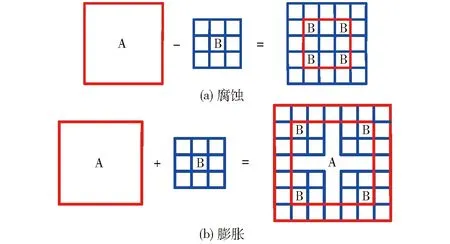
图2 腐蚀膨胀原理图Fig.2 Principle of corrosion expansion

在图像操作中，腐蚀一般用于去除孤立点，膨胀一般用于连接相对靠近的空隙，将腐蚀和膨胀配合在一起使用时，先腐蚀后膨胀被称为开运算，先膨胀后腐蚀被称为闭运算[12]。本文采用开运算，开运算可以在原始位置和形状几乎不变的情况下，去除毛刺和噪点。图3a为预处理前的二值图，为了更加清晰地展示地图特点，选取两处具有代表性的区域进行放大。如放大区域所示，预处理前的地图普遍存在毛边和噪点。在进行开运算时，二值地图中白色区域会先缩小，去除孤立的点，再扩大，连接相对靠近的孤立点。整个开运算过程，可以消除地图上的噪点[13]，连接相距很近却未连续的障碍物边界，平滑地图上的毛边和毛刺，整体区域尺寸和位置几乎不变[14]，预处理结果如图3b所示。地图预处理可以防止后续提取骨架时出现骨架溢出和生成不必要的骨架分支等问题。

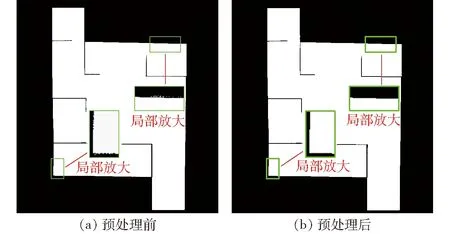
图3 预处理结果Fig.3 Pretreatment result

2 骨架提取

依次遍历图像上的像素点，如图4所示，设此刻遍历到的像素点为P1，其周围的像素点依次标记为P2～P9，设黑色像素点的P值为0，白色像素点的P值为1。由于图像最外围的一圈像素不存在8邻域，所以不对其进行处理。

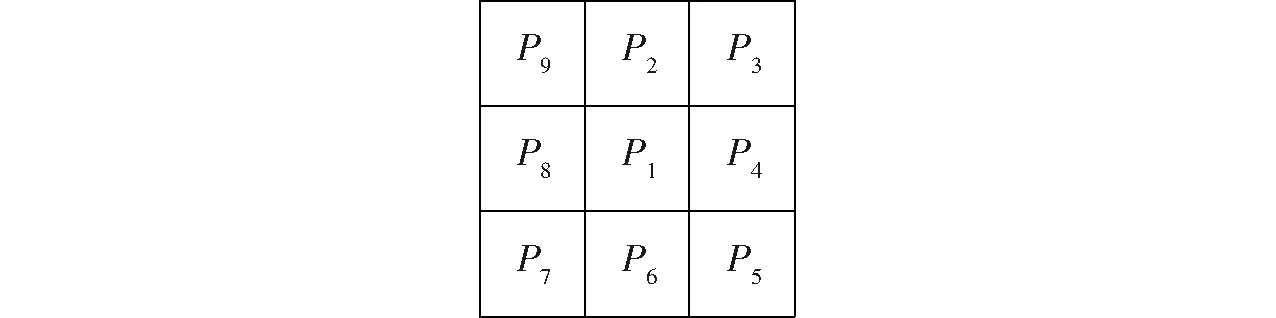
图4 8邻域示意图Fig.4 Eight neighborhood diagram

将点P1的8邻域P2～P9中，P值从0变为1的出现次数设置为M，每个像素的8邻域P值和为N(Px)，将满足表1中条件的P1点像素值设置为0。

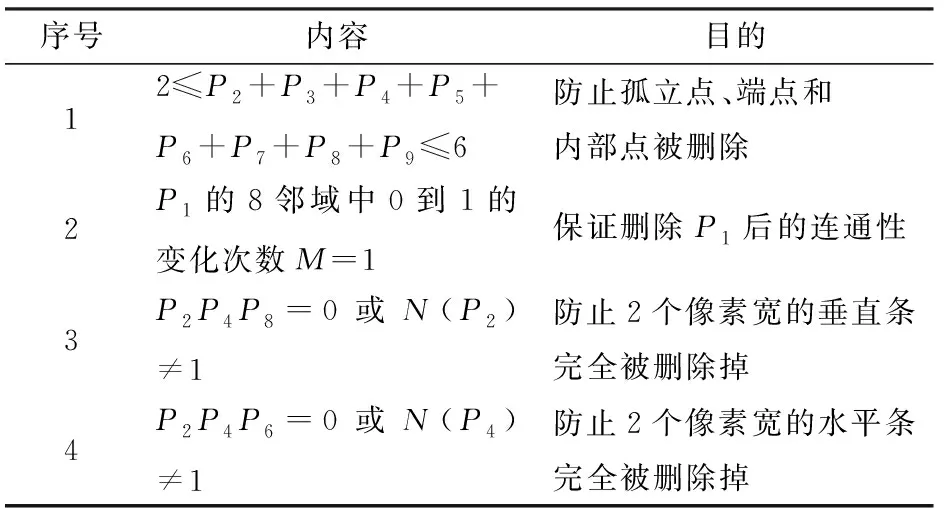
表1 像素值条件Tab.1 Pixel value condition

通过此算法对预处理后的地图进行多次迭代处理，可以得到如图5a所示的骨架[15]，为了表示骨架和原地图的相对关系，将骨架以黑色加载到原地图上得到如图5b所示的骨架全局图，图5c为未对地图进行预处理得到的骨架全局图，通过对比可以发现，未经过预处理的地图由于具有噪点，并且地图边界存在空隙，导致生成的骨架杂乱，甚至溢出边界，无法用于后续导航，经过预处理的地图提取出的骨架清晰简洁，可以为后续导航提供更优质的路线选择。

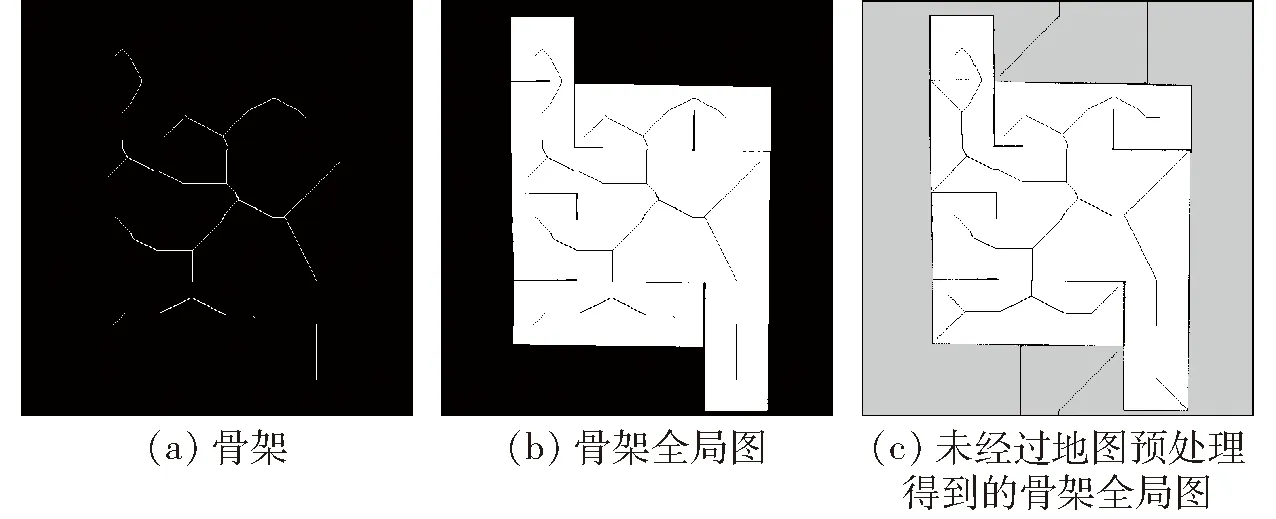
图5 骨架提取结果Fig.5 Skeleton extraction result

3 骨架关键点重规划

3.1 骨架关键点的提取与分类

在生成的骨架图基础上，首先提取出骨架中关键点，将关键点分为端点和分支点两类，端点即为骨架分支的末端点，分支点为骨架的交叉点。为了将骨架上的关键点都找出来，对骨架进行遍历。如图5a所示，由于生成的骨架为像素值255的白色，非骨架部分为像素值0的黑色，在寻找关键点时，主要关注像素值为255的骨架部分[16]。遍历地图中所有骨架点，设每个点的像素值为S，通过分析其如图6所示的8邻域的像素值的和确定其是否为关键点，白点S设为255，黑点S设为0。

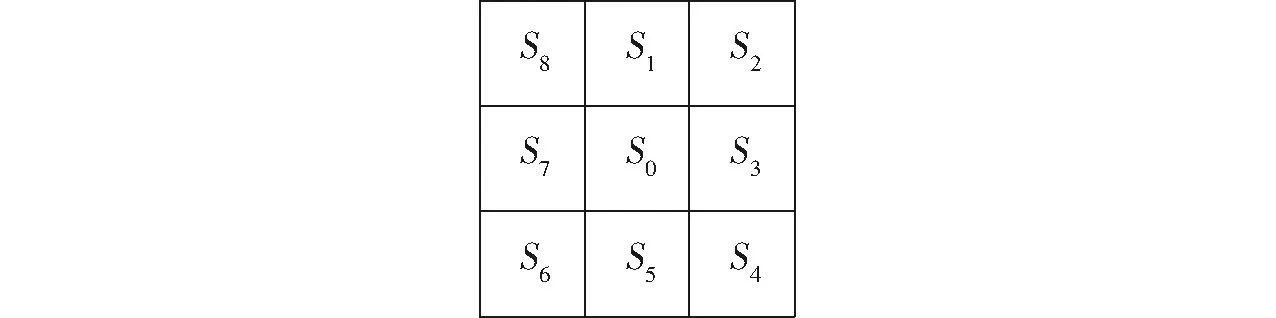
图6 关键点8邻域示意图Fig.6 Schematic of eight neighborhoods of key points

(1)端点确定

骨架端点的8邻域中只有1个像素值为255的白点，因此将满足S1+S2+S3+S4+S5+S6+S7+S8=255的骨架点定义为端点。

(2)分支点确定

骨架分支点是3个分支的交点，即分支点8邻域中会有3个像素值为255的白点，因此将8邻域的和满足表2中条件的骨架点定义为分支点。

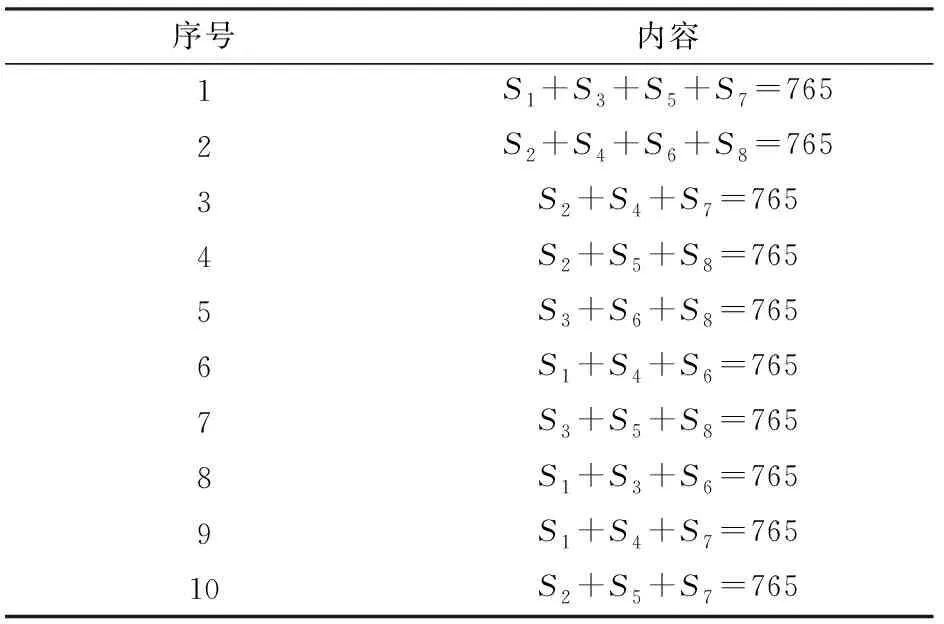
表2 分支点条件Tab.2 Branch point condition

采用上述方法遍历骨架上所有的点，并将骨架和搜索出的关键点以黑色加载到地图上，并将关键点加粗显示，如图7所示，骨架上的所有关键点基本上都被搜索出来。

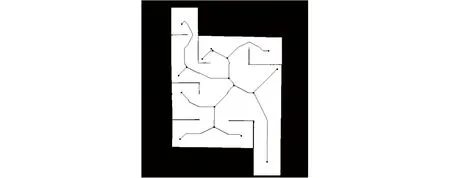
图7 骨架关键点Fig.7 Key points of skeleton

3.2 关键点重规划

在确定关键点后需要进行骨架重规划，骨架重规划首先需要确定各个点之间的连接关系，连接关系共分为2种，一种是端点和分支点的连接关系，另一种是分支点之间的连接关系。

首先，确定端点和分支点的连接关系，遍历所有端点，以某个端点为起点，将所有分支点都设为终点，依次在原始骨架上搜索从该端点到分支点之间的路径。如果搜索出的路径中有且只有设为终点的那一个分支点，则该端点与分支点具有直接连接关系，并将该关系存储起来。

然后，确定分支点与分支点之间的连接关系，遍历所有的分支点，将遍历到的分支点设为起点，其他分支点设为终点，依次在原有骨架上搜索该起点到每个终点的路径。如果搜索到的路径中，有且只有设为终点的那一个分支点，则该端点与分支点具有直接连接关系，并将该关系存储起来。

在明确关键点之间的关系后，将关键点连接起来，连接图像上的2个点，就是将2个像素点连接起来，处理的基本单位是像素[17]。

两点连接一条直线，因为直线的一阶导数是连续的，两点X和Y方向上的间距ΔX和ΔY具有一定的比例关系，Xi+1=Xi+ΔXε，Yi+1=Yi+ΔYε，ε=1/max(|ΔX|,|ΔY|)，采用这个原理[18]，将连线分为以下几个步骤：

(1)确定2个点的坐标。

(2)分别计算X和Y方向上的间距ΔX和ΔY。

(3)确定单位步进，取K=max(ΔX,ΔY)，如果ΔX≥ΔY,则将ΔX方向设为单位步进，ΔX方向每步进一个单位，ΔY方向以ΔY/K的步长向前步进一个单位；否则相反[19]。

(4)设置该点的像素值。

(5)设置循环值为0，循环次数为K，设置2个新的变量X和Y；开始进入以下循环计算：①X向前步进一个单位，Y向前步进一个单位。②设置此时(X，Y)的像素值。

按照以上步骤完成连线后，得到如图8所示的初次连接结果图，图中的骨架经过重新连接后路径变得简洁笔直，但是出现了骨架穿越障碍物的情况，因此在连接前需要加入判断条件并添加中间点。

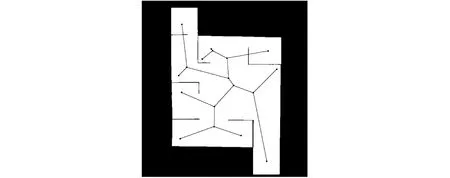
图8 初次连接效果Fig.8 Initial connection effect

3.3 中间点添加

直接将关键点重连后，存在连接线穿越障碍物的问题，因此在连接关键点时需要先进行判断。如果直接连接穿越了障碍物，则需要添加中间点。如图9a所示，点A和点B为具有直接连接关系的中间点，两点之间直线距离为LAB，首先将关键点A、B间的原始连接线4等分，取出中间的3个点M1、M2、M3，分别计算出3个点到直线AB的距离L1、L2、L3，将距离大于0.25LAB的点筛选出来作为连接的中间点，如果重新连接的路线依然穿越障碍物[20]，将原始连接线再次以等分的方式多取出2个点，并使距离阈值自动增加10%，再次进行筛选来寻找中间点，因为原始路线并未穿越障碍物，并且离障碍物较远，所以最终可以搜索出使连接线不穿越障碍物的中间点。最终连接的效果如图9b所示，重规划后的路径笔直，整体Voronoi路径数据量减少。

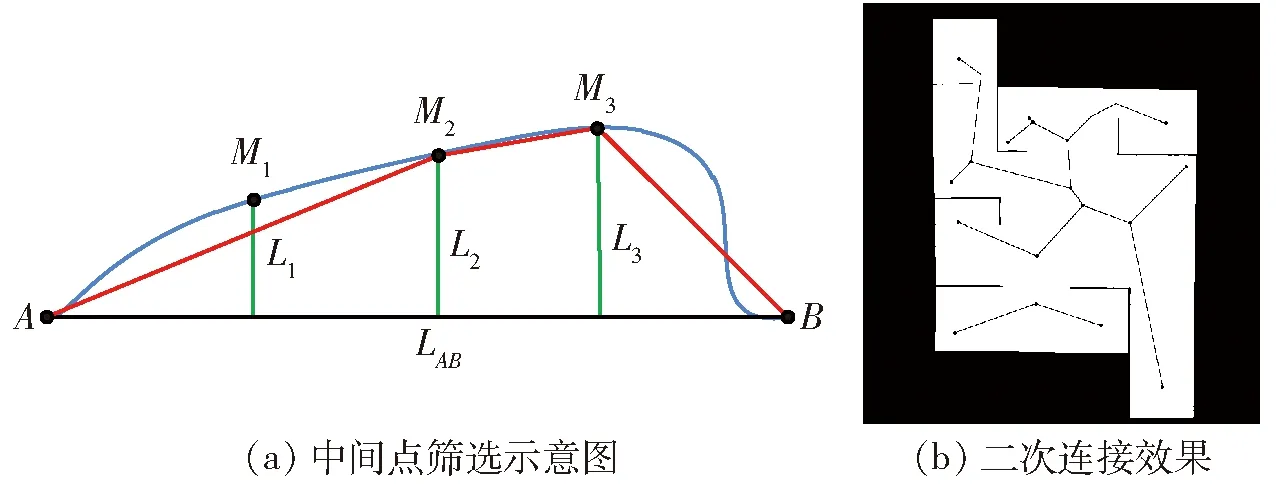
图9 添加中间点示意图Fig.9 Secondary connection effect

3.4 路径平滑

机器人在导航时，会先根据起点和目标点在生成的Voronoi全局路径上寻找出相对应的路径，但是由于Voronoi图的天然缺点，即使采用基于关键点重规划后的Voronoi图生成的路径依然存在锯齿状和转折角度较大等问题[21]。

为了解决该方法中存在的问题，在生成路径时融入改进的降梯度采样方法，优化生成的不平滑路径[22]，优化过程为：

(1)生成的初始路径实质上就是连续的点，将点依次设置为D1(X1,Y1)、D2(X2,Y2)、D3(X3,Y3)、…、Dn(Xn,Yn)。

(2)将平滑后路径上的点依次设置为C1(X1,Y1)、C2(X2,Y2)、C3(X3,Y3)、…、Cn(Xn,Yn)。

(3)定义平滑函数Tsmooth=m(Di-Ci)+k(Ci-Ci+1)，m和k分别代表函数中前后2项的权重，第1项表示平滑后的点与平滑前的点之间的距离，第2项表示相邻的平滑点之间的距离，m较k越大，平滑后的点越靠近原始点，m较k越小，相邻平滑点互相之间越靠近，得到的路径就越平滑，在经过多次反馈分析后，最终选取m为0.5，k为0.4。整个平滑的过程就是将Tsmooth缩小到阈值范围，所以采用梯度下降法不断迭代更新Ci，从而不断缩小Tsmooth。循环迭代表达式为Ci=Ci+m(Di-Ci)+k(Ci-1-2Ci+Ci+1)，通过不断迭代这个表达式，使Tsmooth不断缩小，直到Tsmooth小于阈值0.000 1。

平滑前后效果如图10所示，通过对比，经过平滑后，路径中的锯齿状部分被消除掉[23]，路径转折点更少，转折角度[24]更小，路径更短。

图10 路径平滑对比Fig.10 Path smoothing contrast

4 仿真实验

先通过仿真实验来证明本文算法的可行性。仿真实验在Ubuntu 16.04的系统中基于ROS机器人操作系统进行，主要使用的是Gazebo仿真平台和Rviz图形化工具[25]，其中Gazebo用于搭建三维环境模型，包括机器人本体和周围环境，Rviz用来实时显示机器人运动状态和导航路径。本仿真实验中机器人本体模型为轮式差动机器人，底盘为圆柱形，机器人正上方搭载一台二维激光雷达。

为了验证本文算法的环境适应性和可行性，搭建了2种复杂环境，如图11所示。仿真实验首先建立2种环境的栅格地图，将该地图作为先验信息输入算法，使用本文算法生成相应的Voronoi图用于机器人导航。

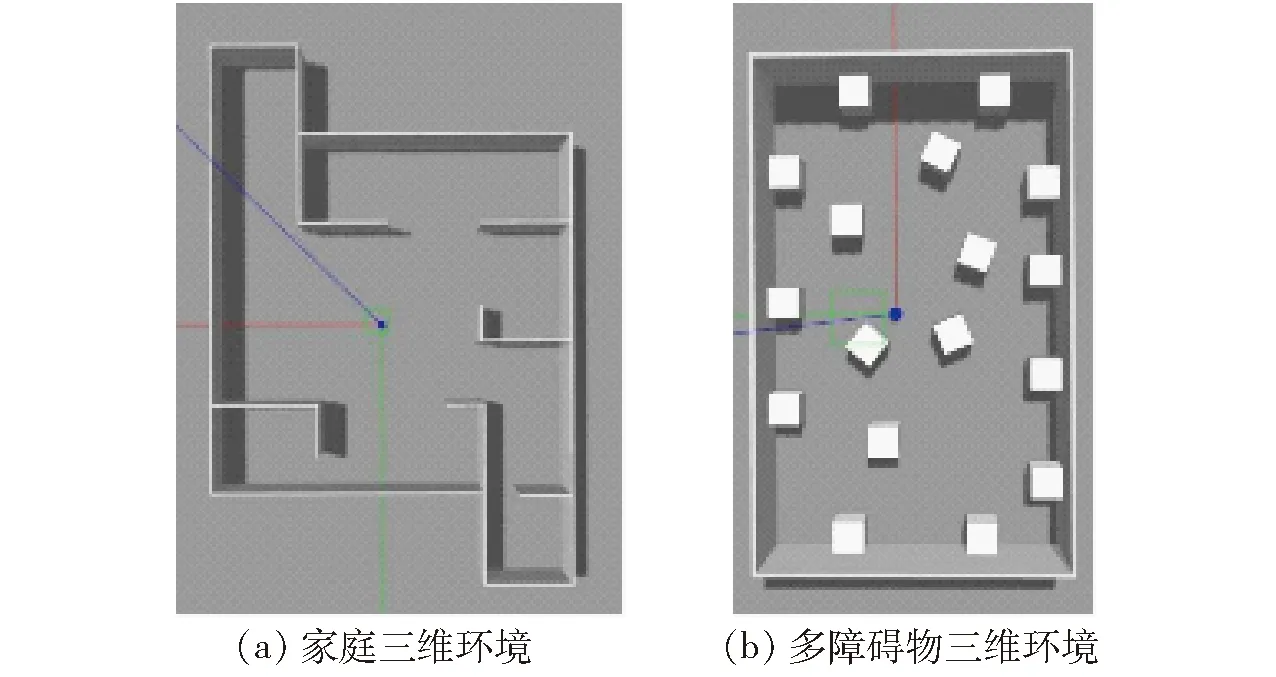
图11 三维环境模型Fig.11 Three dimensional environment models

4.1 栅格地图预处理

图11a为家庭三维环境模型，内部结构仿照家庭环境通过墙体划分为不同区域；图11b为多障碍物三维环境，环境中无规则放置的矩形块代表障碍物[26]。采用建图算法分别构建环境二维栅格地图，使用本文算法对栅格地图进行预处理，如图12、13所示，预处理后的地图与原地图相比噪点更少，边界清晰且完全封闭，可以防止在提取骨架时出现冗余骨架和骨架溢出等问题。

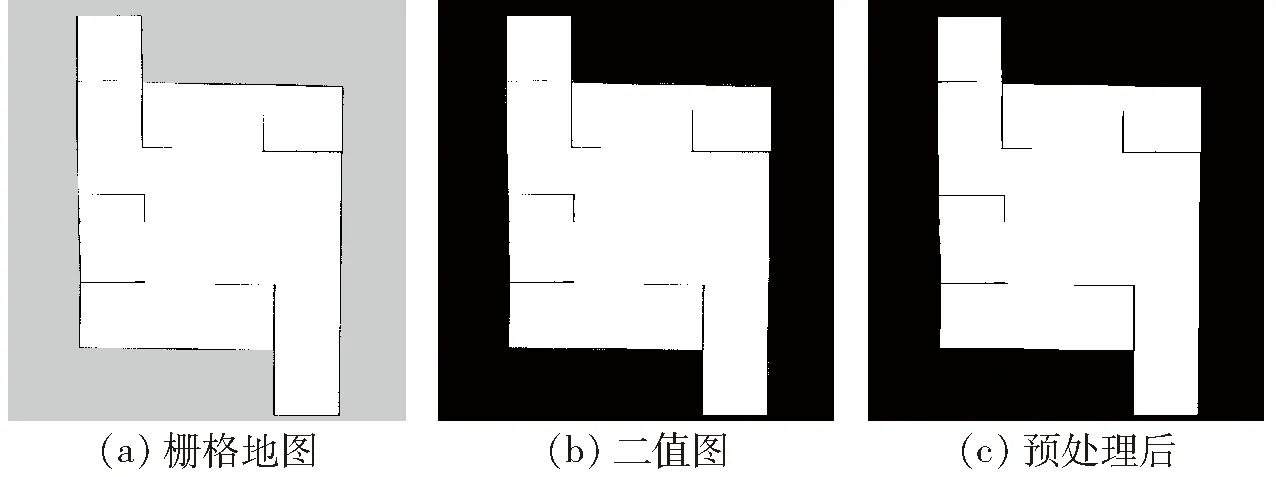
图12 家庭环境地图预处理效果Fig.12 Pre-processing renderings of home environment maps

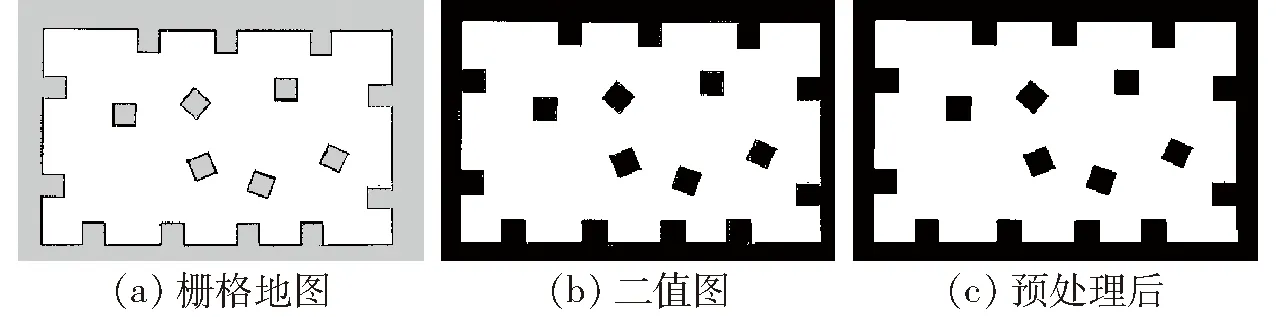
图13 多障碍物环境地图预处理效果Fig.13 Pre-processing rendering of multi-obstacle environment map

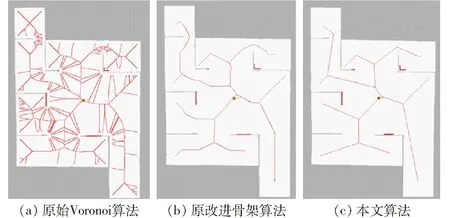
图14 家庭环境骨架对比Fig.14 Family environment skeleton contrast

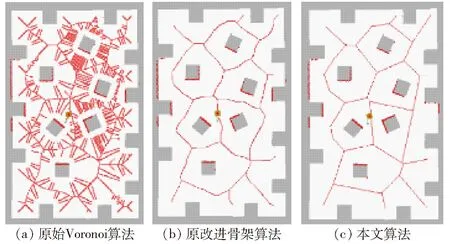
图15 多障碍物环境骨架对比Fig.15 Skeleton comparison of multi-obstacle environment

4.2 骨架提取

栅格地图预处理后进行骨架提取，如图14a、15a所示，原始Voronoi算法[2]由于自身的特点，并且未对栅格地图进行预处理，栅格地图存在噪点，部分边界呈锯齿状，导致生成的Voronoi全局路径有很多非必要的分支；如图14b、15b所示，原改进骨架算法[5]通过改进骨架提取方式精简并优化了生成的全局路径，但生成的路径转折多，转折角度大，长度冗余；如图14c、15c所示，本文算法生成的全局路径笔直，转折极少，转折角度较小。通过比较Voronoi全局路径包含的像素点的数量来比较3种算法分别生成的全局路径数据量。如表3所示，采用本文算法生成的全局路径数据量相对原Voronoi算法生成的全局路径数据量平均降低了82.69%，采用本文算法生成的全局路径数据量相对原改进骨架算法生成的全局路径数据量平均降低了11.81%，因此机器人依据本文算法生成的Voronoi图可以更加快速地规划出路径，机器人导航时具有更好的实时性。

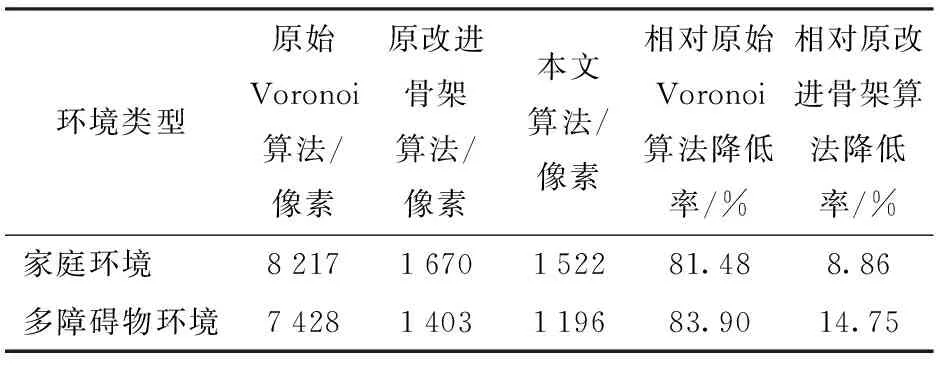
表3 全局路径数据量对比Tab.3 Global path comparison

4.3 路径平滑实验对比

机器人在导航过程中会依据Voronoi图搜索出相应的路径，当机器人的起始点或目标点不在Voronoi全局路径上时，此时就通过图搜索算法连接起点和终点到骨架图上，再基于Voronoi全局路径搜索出起点和终点间的最短路径，得到最终的导航路径[27]。机器人在规划出起始点和终点之间的路径后，就可以开始向目标点移动，但是由于Voronoi全局路径并不平滑，导致搜索出的路径转折次数多，转折角度大，部分路径段呈锯齿状，机器人按照锯齿状路径行走时会依据锯齿多次转向，导致机器人运动缓慢，很大程度上降低了机器人的效率和稳定性[28]。本文针对该问题提出使用降梯度采样法对生成的路径进行平滑处理，平滑前后结果如图16、17所示，为了更加鲜明地对比效果，将图上的局部地区放大2倍，经过本文算法平滑后锯齿状的问题得到解决，路径的转折次数减少，转角变小，转角弧线的长度也变短，路径总长也相应得到缩短[29]，因此经过本文算法处理的路径质量得到了很大提升。

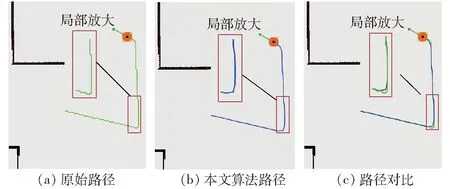
图16 家庭环境路径对比Fig.16 Family environment path comparison

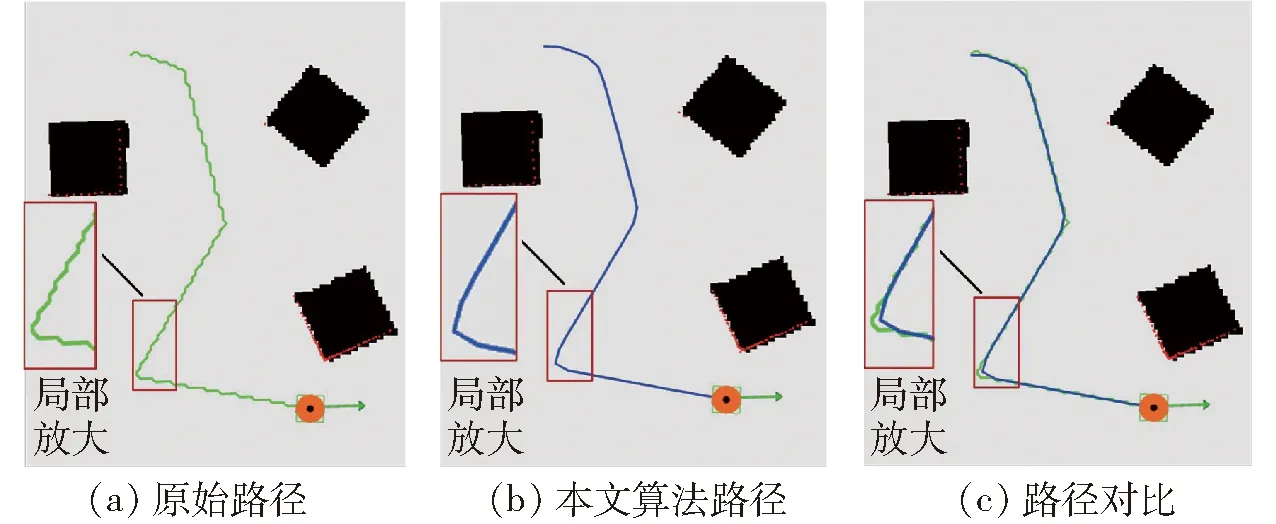
图17 多障碍物环境路径对比Fig.17 Multi-obstacle environment path comparison

4.4 本文算法与原算法生成的路径比较

如图18～21所示，在2种环境中分别选取6组相同的起点和终点，采用2种算法规划出相应的路径，通过对比原算法[5]与本文算法生成的实际路径，可知本文算法生成的导航路径更短，规划速度更快，整体路径更平直，转折少且转折角度小。如表4、5所示，将2种算法规划的路径长度、规划路径的时间，以及规划路径中转折次数进行对比，其中规划路径长度用路径中包含的像素数表示。由表4、5可知，在2种环境下共规划的12组路径中，本文算法相对于原算法规划出的路径长度平均减少了11.43%，规划路径的时间平均减少了15.65%，转折次数平均减少了51.13%。由此证明本文算法相对于原算法在规划路径质量和规划路径实时性上有明显优势。

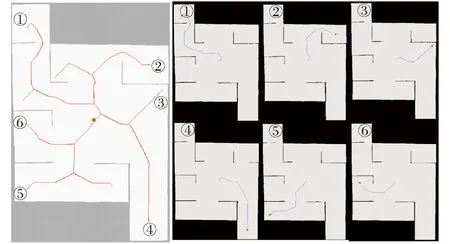
图18 基于原改进骨架算法家庭环境导航路径Fig.18 Home environment navigation path based on improved skeleton algorithm

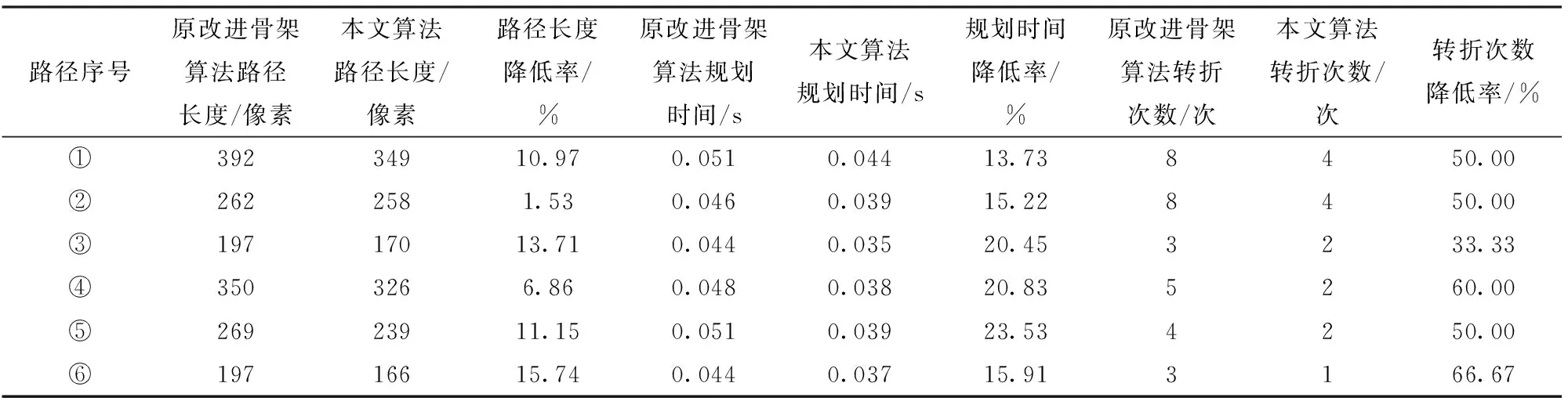
表4 室内环境下规划路径参数Tab.4 Planning path parameters in an indoor environment

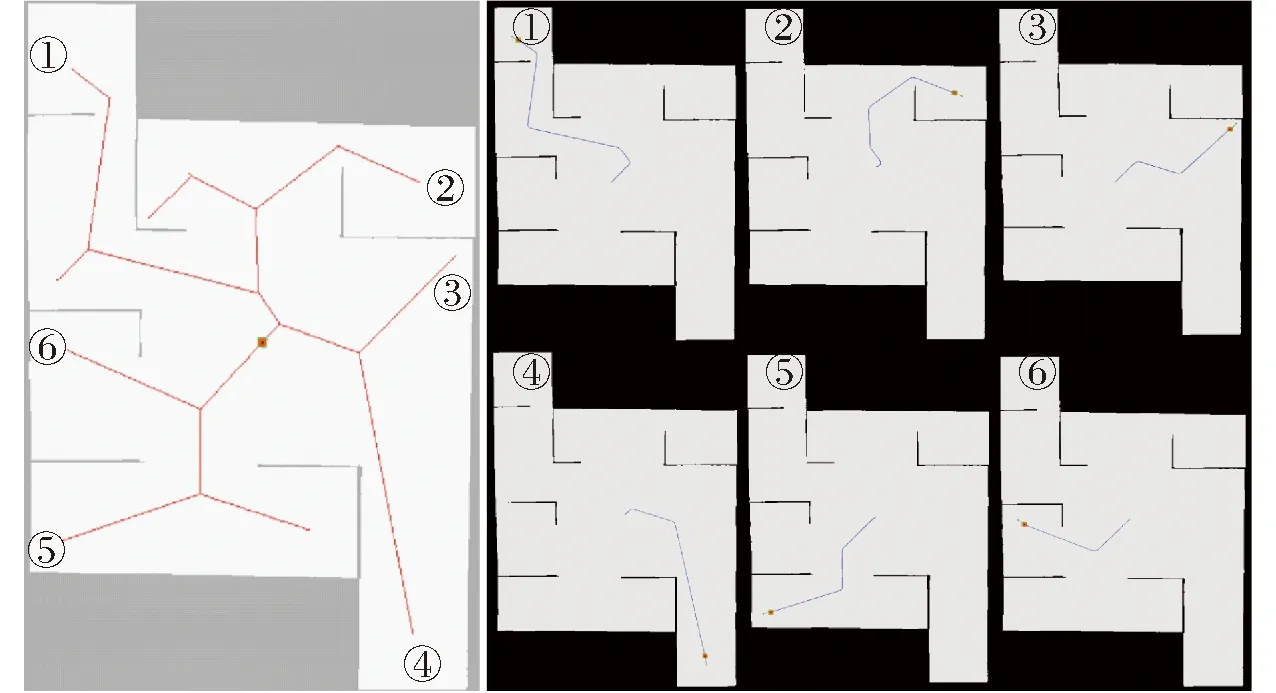
图19 基于本文算法家庭环境导航路径Fig.19 Home environment navigation path based on proposed algorithm

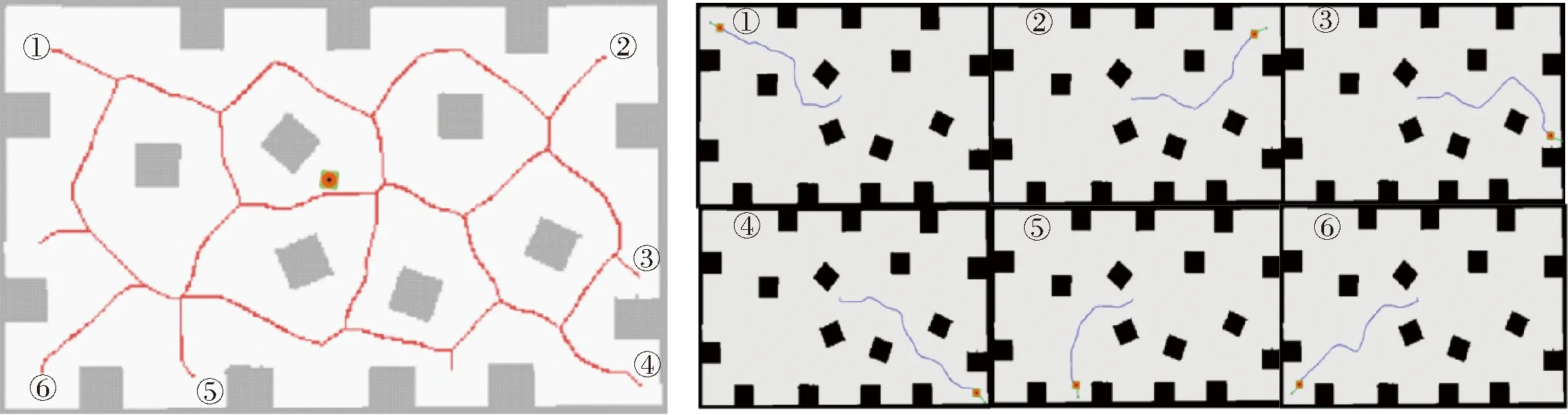
图20 基于原改进骨架算法多障碍物环境导航路径Fig.20 Multi-obstacle environment navigation path based on improved skeleton algorithm

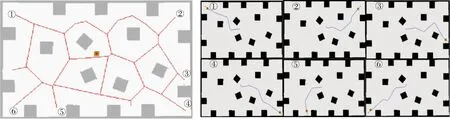
图21 基于本文算法多障碍物环境导航路径Fig.21 Multi-obstacle environment navigation path based on proposed algorithm

5 实际实验

通过多次仿真实验基本证明了本文算法的可行性和稳定性后，在实际环境中对本文算法进行验证，实际环境中使用的机器人为本实验室自主搭建的轮式差分机器人。如图22所示,该机器人由机械部分、传感器部分、控制器部分组成；机械部分主要包括连接件和玻璃纤维加工板；传感器部分主要由SICKlms111型激光雷达、光电编码器、KinectV2相机构成；控制器由Intel-NUC和驱动控制器构成。

图22 实验平台Fig.22 Experiment platform1.供电电池 2.Intel-NUC 3.显示器 4.激光雷达 5.光电编码器

在实验室搭建如图23a所示实验场景，该场景通过围墙将实验室划分为不同尺寸和形状的区域，并在墙角部分放置一定数量的柜子。机器人在该环境中使用Gmapping建图算法构建如图23b所示栅格地图，采用本文算法对地图进行预处理并生成Voronoi图。

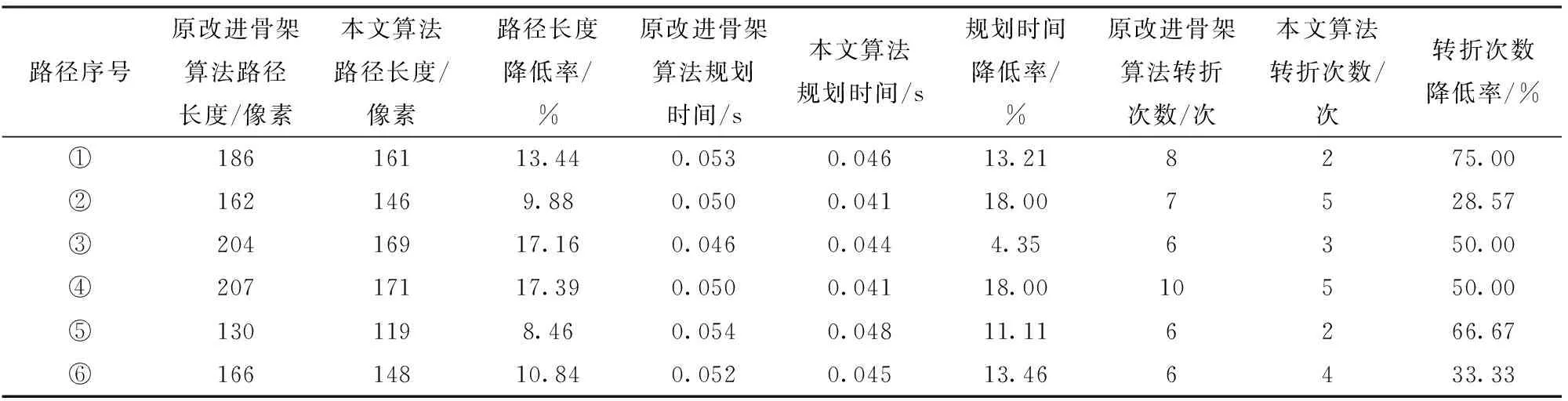
表5 多障碍物环境下规划路径参数Tab.5 Planning path parameters in a multi-obstacle environment

图23 实际实验环境Fig.23 Actual experimental environment

通过2种算法生成的Voronoi图如图24所示，图24a为原改进骨架算法[5]生成的Voronoi图，整体路径清晰简洁，但路径弯曲冗长，转折次数多，图24b为本文算法生成的Voronoi图，路径笔直简洁，数据存储量也在一定程度上有所降低。

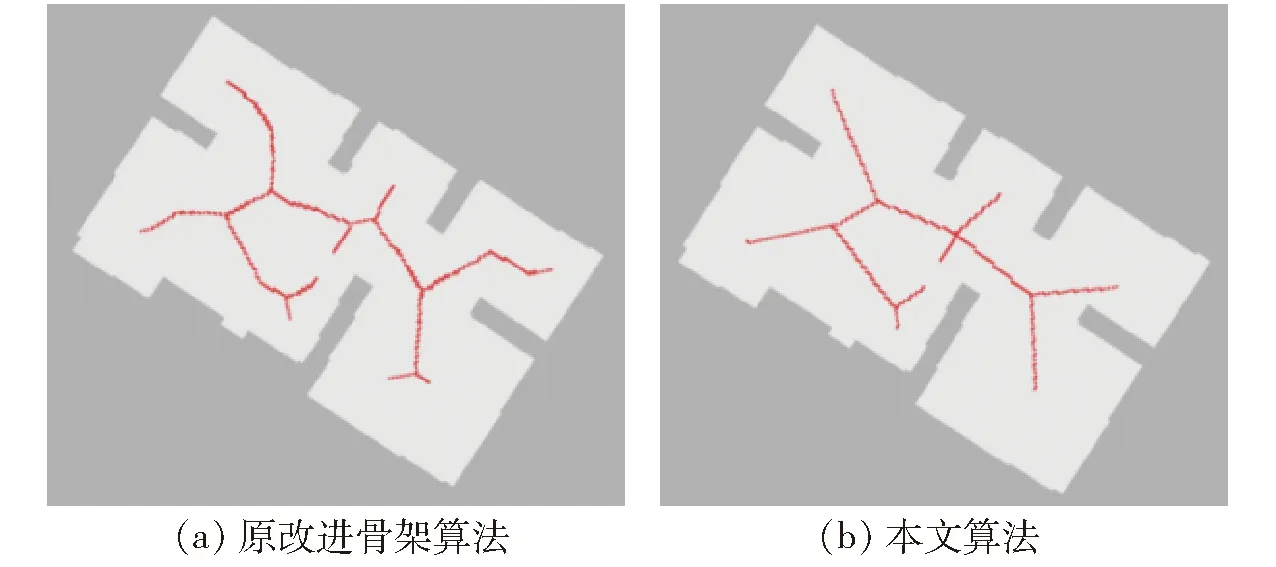
图24 实际实验骨架Fig.24 Actual experimental skeleton diagram

在实际实验中，机器人利用原改进骨架算法和本文骨架算法生成的Voronoi图分别进行导航，在相同起点和终点的条件下，规划路径如图25、26所示。图25a、26a和图25c、26c为基于原改进骨架算法[5]和本文算法生成的Voronoi图规划出的导航路径1和路径2，图25b、26b和图25d、26d为使用Odometry记录的实际导航路径。对比机器人采用原改进骨架算法[5]和本文算法走出的实际路径，依据原算法进行导航时，机器人实际运行路径长且存在很多大角度转向，原算法由于生成的Voronoi图弯曲，导致机器人依据原算法规划出的路径导航时转折次数多且转折角度大，大角度转向时，机器人会减速，极大地降低了机器人的导航效率，总体运动路径不合理；依据本文算法进行导航时由于最终生成的Voronoi图笔直，不仅在原算法的基础上缩短了路径，笔直的路径相对于原算法的弯曲路径消除了不必要的转向，提高了机器人的导航效率，整体运动路径也更加合理。

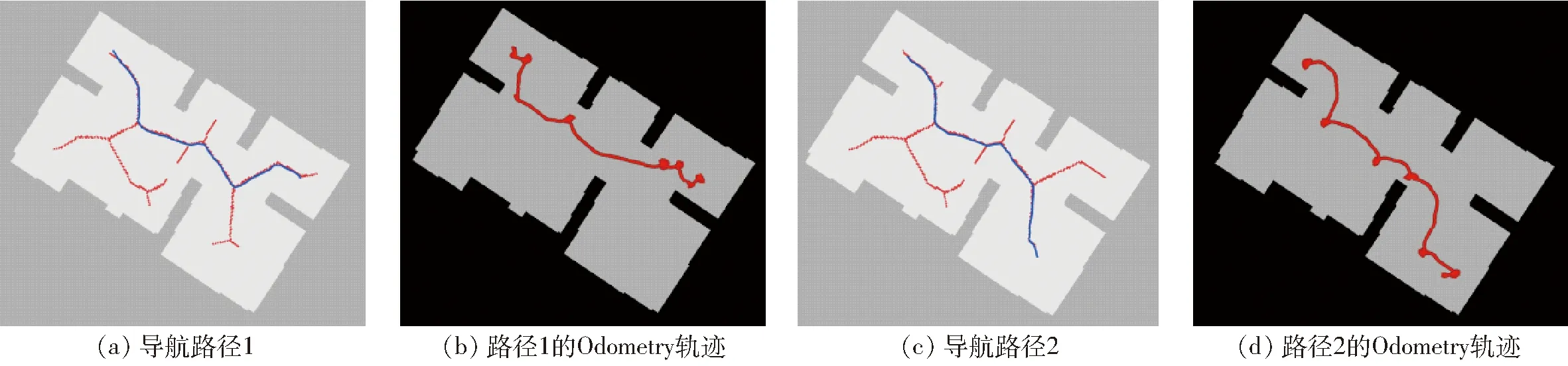
图25 原改进骨架算法实际导航路径Fig.25 Actual navigation path of original improved skeleton algorithm

图27展示了机器人采用本文算法在实际环境中的运行情况。机器人基于本算法运动时能够避开障碍物并快速到达目标点。

图26 本文算法实际导航路径Fig.26 Actual navigation path of proposed algorithm

图27 机器人实际运行情况Fig.27 Actual operation of robot

6 结束语

针对现有的Voronoi算法生成的Voronoi地图路径弯曲冗余，依据Voronoi地图规划路径时实时性较差，机器人导航时转折次数多，角度大，时间成本高等问题，采用提取骨架中关键点，并基于关键点重规划的方法,解决Voronoi地图路径弯曲冗余的问题，得到的骨架相对于原改进骨架算法的数据量更加精简，机器人依据本算法生成的数据量精简后的Voronoi地图规划路径时更加快速，规划出的路径更短、质量更高，并且对规划出的路径进行降梯度采样平滑处理，尤其是对转角路径进行降梯度采样，既平滑了转角处路径，又缩短了转角路径长度，机器人在运动过程中转向次数减少，从而提高了机器人的导航效率。