基于数据驱动模型融合的锂离子电池多时间尺度状态联合估计方法*
王 萍,彭香园,程 泽,张吉昂
(天津大学电气自动化与信息工程学院,天津 300072)
前言
锂离子电池具有自放电小、能量密度高、循环寿命长等优点,在电动汽车领域受到广泛重视。为保障电池的安全和最佳使用,有必要配备电池管理系统(battery management system,BMS)。其中准确的状态估计是BMS的关键环节,包括荷电状态(SOC)、健康状态(SOH)和剩余使用寿命(RUL)。这3个状态参数从不同方面保障电池长期平稳运行,但均无法由传感器直接测得。
SOC定义为剩余容量占其最大可用容量的比值,属于微观尺度的变化。安时积分法由于其简单和易于实现在BMS中得到了广泛的应用,但初始SOC难以获得,且作为一种开环方法存在误差累积的问题。开路电压(open circuit voltage,OCV)法常与安时积分法结合用于初始SOC的校准,但需要电池的长时间静置,不适合在线使用。相比之下,基于等效电路模型(ECM)的方法由于其自校正能力、鲁棒性强以及精度高的优点得到了广泛关注。该类方法主要利用一组状态方程并结合滤波算法进行闭环SOC估计,常用的滤波算法有卡尔曼滤波(Kalman filtering,KF)、H滤波(Hfilter,HIF)和粒子滤波(particle filter,PF)等。但ECM的参数受工作环境以及自身状态变化的影响,有必要为模型参数辨识以及SOC估计设计一个联合估计框架以实现较高的估计精度和鲁棒性。
现有针对两者的联合估计方法相当有限,大致分为两类。第一类将模型参数和OCV合并为一个向量,用递推最小二乘(recursive least squares,RLS)或者KF法进行联合估计,随后由OCV-SOC关系获得SOC值,优点是只需要一个自适应滤波器即可获得所有所需参数,缺点是若电池模型不准确,则会出现SOC估计不稳定甚至发散现象。第二类方法用并行滤波器以一种闭环的方式同时估计参数和SOC,因此有较高的精度。但上述两种方法并没有解决对SOC估计同样至关重要的容量更新问题。
容量可以用来定量评估电池老化程度,一般用当前最大可用容量和初始容量之间的比值定义电池的另一个重要的状态参数SOH。容量包含在基于ECM的滤波算法的计算中,因此容量的准确和实时更新对SOC估计至关重要。文献[10]和文献[11]中分别采用双非线性预测滤波(dual nonlinear predictive filter,DNPF)和双扩展卡尔曼滤波(dual extended Kalman filter,DEKF)对容量和SOC进行联合估计,但没有自适应调整模型参数或者只是部分调整。Wei等采用RLS辨识模型参数,用DEKF估计容量和SOC。然而两个滤波器采用相同的时间尺度且并行工作大大增加了计算负担。随着大数据以及机器学习等新兴技术的发展,可以考虑用老化数据离线建立模型,避免物理建模和参数辨识问题,灵活性较强,但该类方法的精度和可靠性高度依赖于与SOH相关的健康特征(HF)的选择。
RUL(remaining useful life,RUL)通常定义为到寿命终止(end of life,EOL)时电池的剩余充放电循环周期数,用于衡量电池在其生命周期的可靠度,是宏观尺度下对电池未来状态的描述,而SOH属于宏观尺度下对当前状态的描述。为了全面评价电池的老化程度,须同时进行SOH估计和RUL预测。然而,目前对于SOC-SOH的联合估计较为常见,RUL预测通常单独进行。例如文献[16]中提出一种指数和多项式相结合的组合模型法,并用PF对模型参数在线更新,实现RUL预测。这类模型法较为简单,但通常只能提供点预测结果,在RUL长期预测中表现不佳。此外,使用机器学习的数据驱动法也被广泛应用于RUL预测中。Wang等将能量效率和平均工作温度作为SVM输入,电池当前容量和该循环周期容量的下降值为输出,建立了多步容量预测模型。机器学习算法可以对非线性系统精准建模,但其多步迭代预测的能力较差,通常只能进行单步预测。单一方法很难实现RUL的精准预测,融合算法是目前的研究方向,此外,RUL是对未来的状态进行描述,需要提供预测结果的不确定性表达,以提升预测的可靠性。
综上所述,上述研究存在以下问题:一是SOC、SOH和RUL三者之间存在着耦合和步骤重叠的问题,单独估计不能保证精度同时也增加了计算量,例如SOC估计必不可少的前提是电池容量和模型参数的实时校准,RUL长期预测的前提是对当前SOH的精准可靠估计。二是电池参数、SOH和RUL随时间变化缓慢,而SOC随时间变化迅速,因此使用相同的时间尺度不能得到准确可靠的估计值,且大大增加了控制系统的计算量,降低稳定性。
为此,本文中提出一种基于模型数据驱动融合的锂离子电池多时间尺度状态联合估计方法。首先建立戴维南模型,采用最小二乘(least square,LS)辨识阻容参数,提取内阻作为HF,建立LSSVM电池老化模型,实现SOH估计;利用GPR对内阻随循环次数的变化进行映射,预测内阻的变化趋势,并结合LSSVM模型实现RUL预测。用阻容参数辨识值和SOH估计值更新状态空间方程,采用UKF算法实现放电阶段的SOC估计。在牛津数据集中进行验证,结果表明所提方法具有较高精度和鲁棒性。
1 在线参数辨识和健康特征提取
本文选取牛津数据集,标记为Cell1~Cell 8。数据集的详细介绍请参照文献[21]。
1.1 戴维南等效电路模型
考虑到计算量和精度,本文建立1阶戴维南等效电路模型,如图1所示。

图1 戴维南等效电路模型
其中:I表示输入电流;U为端电压;R为欧姆内阻;R和C分别表示极化电阻和极化电容;U为开路电压,与SOC相关,即U=f(SOC),一般在实验室环境下通过小电流充放电获取,然后采用多项式拟合。由于一次U测试耗时较长,且文献[22]中指出f受电池老化的影响较小,在全生命周期内变化不大,故这里选用新电池的U-SOC曲线。
根据基尔霍夫电压电流定律,可得
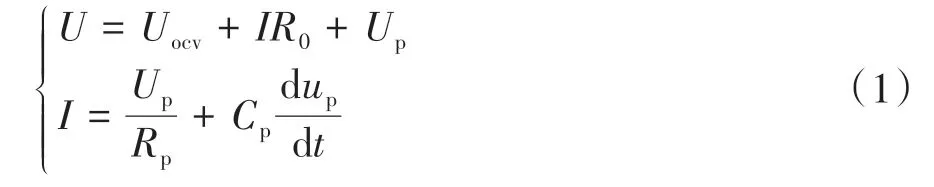
1.2 在线参数辨识
考虑到模型参数随电池老化而变化,模型参数需在线更新以提高状态估计精度。
电池放电工况复杂多变,而充电工况一般采用恒流恒压固定充电模式,可用于在线参数辨识。恒流充电下的SOC的表达式为

式中Q(n)表示第n次充放电循环下的可用容量,此时的健康状态计算公式如式(3)所示,式中Q为电池的出厂容量。

结合式(1)和式(2),可得不同循环次数下恒流充电的电池端电压的变化特性,如式(4)所示,各变量上标n表示循环次数n。
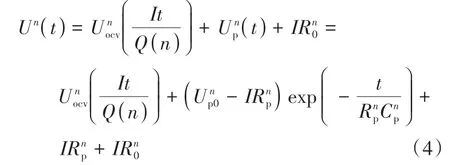
可以看出,模型参数以及容量随循环次数的更新,属于宏观尺度;SOC是时变参数,属于微观尺度,且受到宏观尺度参数的影响,这里也体现了多时间尺度状态联合估计的必要性。
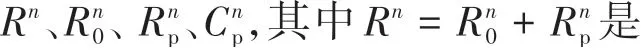

图2 Cell1标准化阻容参数和SOH的变化趋势
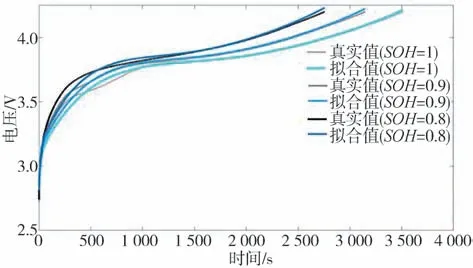
图3 Cell1的电压真实值和模型输出值
1.3 相关性分析和健康特征提取
锂离子电池的老化原因主要有3种:(1)锂离子损失(loss of lithium inventory,LLI),(2)活性物质的损失(loss of active material,LAM),(3)电阻增加(resistance increase,RI)。LLI主要来源于固体电解质界面(solid electrolyte interphase,SEI)的形成和电解液分解引起的副反应消耗了可循环锂;LAM直接影响电池的可用容量;RI是电极和电解质降解的结果,且LLI和LAM都会导致RI。由图2可以看出,电阻随循环次数的增加而增大,与老化机理一致,定性表明电阻可以反映电池老化信息。
选用Pearson相关系数和灰色关联度(grey relation coefficient,GRC)进一步定量评价各参数与SOH的相关性:
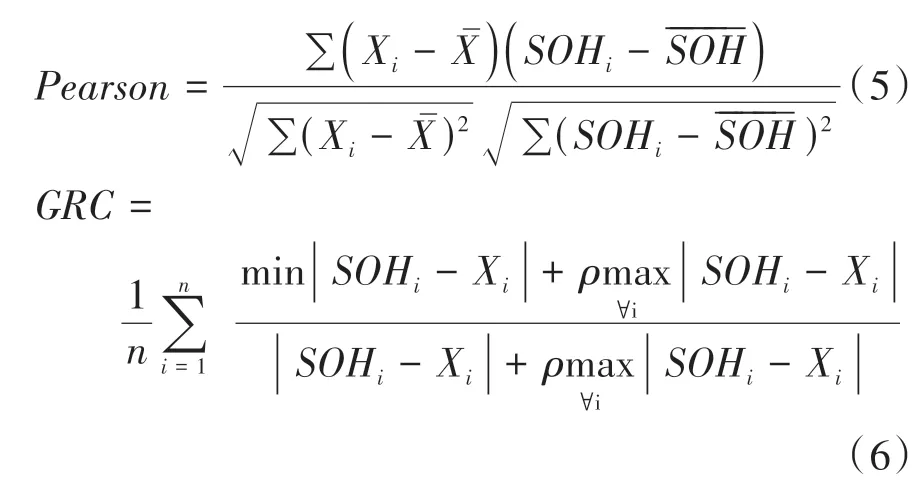
式中:X为第i次循环的阻容参数;SOH为第i次循环的SOH值;n为循环总数;ρ为分辨系数,一般取0.5。计算结果列于表1,绝对值越接近1,说明相关性越高。
从表1可以看出,R与SOH的相关性最高,Pearson系数的绝对值在0.98以上,GRC在0.9以上,与老化机理一致,故直接选取内阻R为HF。
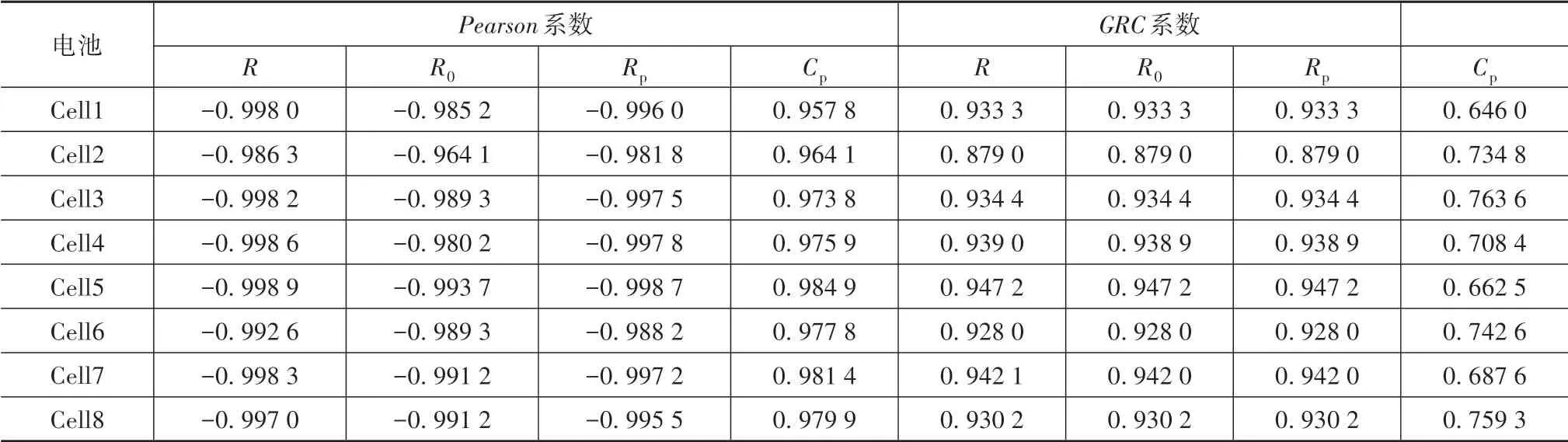
表1 阻容参数与SOH的Pearson和GRC系数
2 联合估计方法
2.1 UKF算法
本文模型部分主要是戴维南模型结合UKF。UKF算法基于UT变换技术,与其他KF系列方法相比,避免了求导运算,对状态方程的要求低,同时对方差的估计更为准确。

状态量的初始值和初始误差协方差矩阵分别为

式中:λ是Sigma点的尺度参数,λ=α(n+κ)-n,α描述Sigma点偏离状态值的程度,满足10≤α≤1,κ是副尺度参数,为保证方差半正定,满足κ≥0,一般在状态估计时取0,在参数估计时取3-n;β是一个与Sigma点分布相关的量,当Sigma点成高斯分布时,通常β=2。
(2)预测阶段
采样时刻k,Sigma点构建的矩阵为

2.2 LSSVM算法


2.3 GPR算法



2.4 SOC-SOH-RUL联合估计框架
为提高估计精度,减少计算量,本文中提出一种锂离子电池多时间尺度状态联合估计框架,用微观尺度估计SOC,用宏观尺度估计电池参数、SOH并进行RUL预测。整体流程图如图4所示。

图4 锂离子电池SOC-SOH-RUL联合估计框图
第一步:老化建模。对预测起点(starting point,SP)之前的循环周期,建立戴维南模型,采用LS算法辨识阻容参数,提取内阻作为HF,建立LSSVM电池老化模型。
第二步:SOH估计。对于第N次循环(N>SP),辨识当前循环下的内阻值作为HF,输入LSSVM老化模型中进行SOH估计。

3 联合估计结果与分析
选用相对误差百分比(relative percentage error,RPE)、平均绝对误差(mean absolute error,MAE)以及均方根误差(root mean squared error,RMSE)对估计结果进行定量评估,x和x^分别表示真实值和估计值:
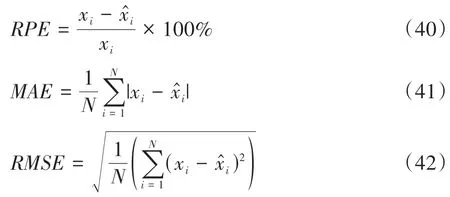
Cell1~Cell 3、Cell 7和Cell 8的标准化周期数约为80,SP设为30。Cell 4~Cell 6的标准化周期数约为50,SP设为20。电池EOL设为0.8,EOL以后的状态估计不在本文考虑的范围内。
3.1 SOH和RUL估计结果
以Cell 1、Cell 4为例,图5展示了SOH估计和RUL预测结果及误差,绿色和蓝色虚线分别表示SP和EOL,可以看出SOH预测轨迹均能反映真实的衰退趋势。所有电池误差的MAE和RMSE列于表2,各电池SOH估计的RPE均在1%以内,MAE和RMSE在0.5%以内,验证了本文所选HF—内阻能够很好地表征电池的老化,并能适应电池不一致性带来的容量衰退趋势差异。同时表明LSSVM算法具有较强的非线性映射能力,在数据量较小的样本(Cell 4~Cell 6)中也能实现SOH的准确估计。
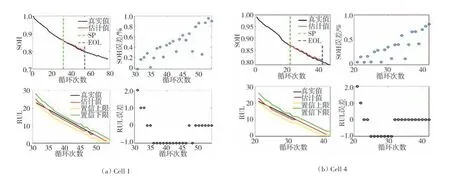
图5 SOH估计和RUL预测结果以及误差
此外由图5可知,各周期RUL预测值(红线)与真实值(黑线)非常接近,最大误差为2,且持续周期数较少。而且可以发现,越接近EOL,RUL预测效果越好,预测误差均为0个周期,这在实际行驶中是非常有意义的,因为越接近EOL,越需要RUL的精准预测值,以及时发现电池的异常状态,降低风险并提高电池的可维护性。绿线和黄线分别表示RUL置信区间的上下限,估计值和真实值都落在置信区间里,且置信区间的宽度较窄,表明估计结果具有较高的可靠性。SP取值分别是20和30,表明即便在数据量很小情况下,GPR算法也能够通过循环次数外推预测HF的变化趋势,并结合LSSVM模型对容量衰退趋势进行预测,实现RUL预测。以Cell 7为例,图6和图7分别展示了不同循环次数下对内阻和SOH衰退趋势预测的结果,由图可知外推值虽然不能完全刻画特征和容量的波动,但是能够很好地跟随内阻和SOH衰退的实际趋势,从而保证了RUL预测的准确性。表2定量给出了所有电池的RUL预测误差,各电池MAE均小于1,RMSE最大值为1.172 6,表明所提方法具有较高的精度和稳定性。
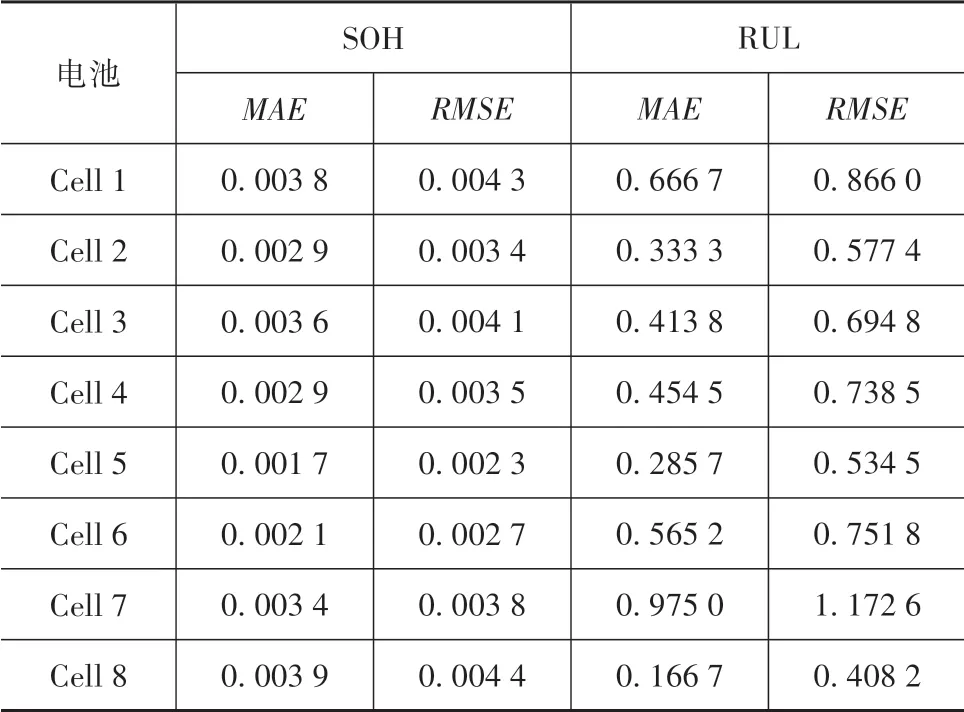
表2 SOH和RUL估计误差
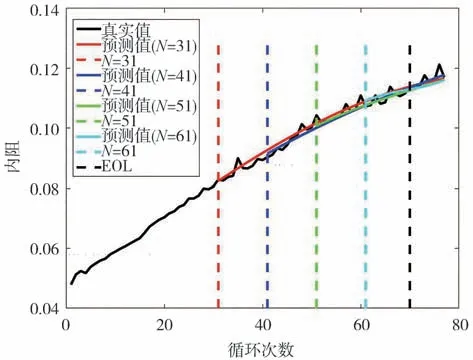
图6 Cell 7的内阻趋势预测
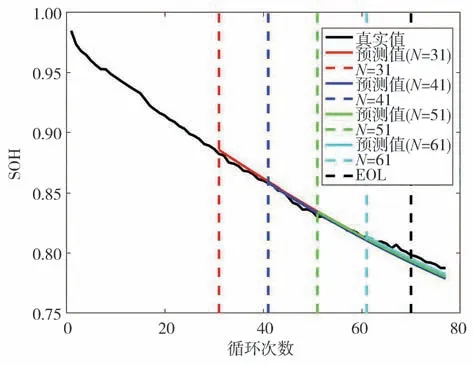
图7 Cell 7的SOH衰退趋势预测
3.2 SOC估计结果
图8 展示了各电池SOC估计结果。实际中SOC初值通常难以获得,为验证算法的鲁棒性,设置SOC的初始误差为0.5。定义跟随时间为SOC估计值与真实值的误差小于0.1的时间和放电总时间的比值,计算跟随时间之后的MAE和RMSE,其随循环次数的变化趋势如图8(a)~图8(h)的下图所示。从SP到EOL的总循环次数中取两次循环,两次循环周期的放电阶段SOC估计效果如图8(a)~图8(h)的上、中两张图的红线所示。
可以看出,SOC估计的初始误差较高,但可以很快跟随真实SOC曲线,不同循环次数下的跟随时间都在0.06左右,反映了UKF算法较强的鲁棒性。随着电池接近EOL,SOC的估计误差稍大,这样的误差主要来源于参数和SOH估计误差,但整体来看,各电池各循环周期的MAE和RMSE均在3%以内,满足误差要求。图8(a)~图8(h)的上、中两张图的蓝色曲线是SOC单独估计的效果,即UKF的状态和观测方程的阻容参数设为常数,Q(n)设为额定容量,不随电池老化自适应更新,此时SOC出现了明显的偏离,且随着电池老化更加严重。而采用本方法,阻容参数和当前容量可以随电池老化的进行而自适应调整,因而提高了ECM的适应性,在电池全寿命周期都能取得较高的SOC估计精度。

图8 SOC估计结果和误差
4 结论
本文中提出了一种基于等效电路模型和数据驱动融合的锂离子电池多时间尺度状态联合估计方法。主要工作如下:
(1)建立戴维南模型,每个循环周期下,对充电电压曲线采用LS辨识阻容参数;
(2)直接提取ECM内阻作为HF,该HF能表征电池老化机理,减少了额外提取HF的计算量,建立LSSVM电池老化模型实现SOH估计;
(3)利用模型参数辨识值和SOH估计值自适应更新状态方程矩阵参数,采用UKF算法实现放电阶段SOC估计;
(4)采用GPR对内阻随循环次数的变化趋势进行建模,通过循环次数的外推实现内阻变化趋势预测,结合LSSVM老化模型实现RUL预测;
(5)在牛津数据集的8个电池上进行实验验证,结果表明所提方法能够实现多时间尺度状态的准确、鲁棒估计。
下一步将在其他类型电池以及更为复杂工况下进行验证。

